Исследование операций 2


Нормоконтролёр:
Плотникова Н. В.________________
«____» ___________ 2005 г.
Руководитель:
Плотникова Н. В._______________
«____» ___________ 2006 г.
Автор:
Студент группы ПС-346
Артемчук Г.Н.
«____» ___________ 2006 г.
Работа защищена
с оценкой
«____» ___________ 2006 г.
Содержание
Задача 1
Формулировка
Заводу, выпускающему прокат, грозит банкротство. Поэтому возникла необходимость оптимизации выпускаемого ассортимента для достижения максимальной прибыли. Известны параметры выпускаемых изделий.
В день со склада может поступать не более 50 тонн медных заготовок и не более 15 тонн алюминиевых. Трубы и прутки изготавливают из меди, а проволоку и ленту – из алюминия (и хранят их в бобинах). Площади складских помещений позволяют складировать бобины с лентой и проволокой в стык длиной не более 5 м. Стойки для труб и прутков стоят в 5 рядов по 16 метров для каждого ряда. Количество брака за сутки не должно превышать 0.19 тонн металла. Энергозатраты не должны превышать по договору с электростанцией 225 тыс. руб.
Вид проката
Масса металла для производства тонны продукции, тонн
Доход от производства, тыс. руб.
Длина единиц хранения, м
Брак, %
Энергозатраты, тыс. руб.
Трубы
1,2
8
3,5
1
6
Прутки
1,2
7
3
0,5
5
Проволока
1,18
5
0,5
0,2
7
Лента
1,1
3
0,8
0,1
3
Решение
Составим математическую модель задачи. Возьмём в качестве целевой функции прибыль от продажи выпускаемого ассортимента, а в качестве переменных - выпускаемые изделия: х1 - трубы, х2 - прутки, х3 -проволока, х4 - лента.
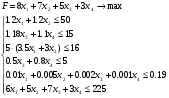
Приведем к ОЗЛП:
Добавим переменные y1, y2, y3, y4, y5, y6.
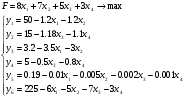
Так как имеется 6 уравнений и 10 неизвестных, то задачу будем решать симплекс методом.
Приведем к стандартному виду:
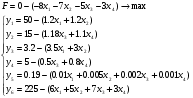
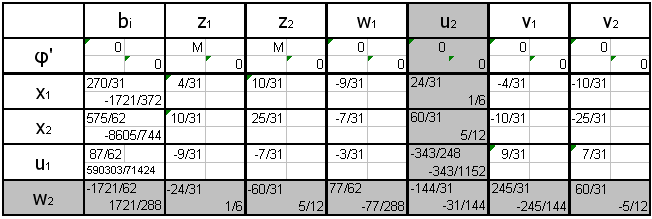
Составим симплекс таблицу:
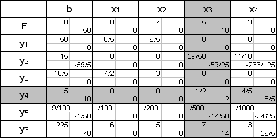



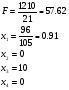
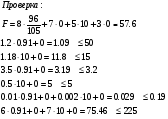
Для достижения максимальной прибыли заводу необходимо оптимизировать выпускаемый ассортимент следующим образом:
Трубы – 0,91 тонн
Прутки – 0
Проволока – 10 тонн
Лента – 0
Только при данной оптимизации ассортимента доход завода будет максимален и составлять 57.6 тыс. руб. в день.
C1
C2
C3
C4
C5
C6
B1
B2
B3
Знаки ограничений
1
2
3
5
1
-1
1
2
0
4
16
4
=
=
=
A11
A12
A13
A14
A15
A16
A21
A22
A23
A24
A25
A26
-2
4
2
0
0
0
8
2
2
4
2
0
A31
A32
A33
A34
A35
A36
Тип экстремума
2
2
0
0
2
0
max
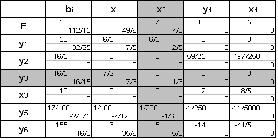
Представление условия задачи в стандартном виде:
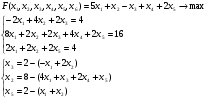
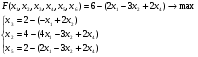
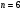 - неизвестных,
- неизвестных, 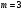 - базисных,
- базисных, 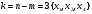 - свободных.
- свободных.
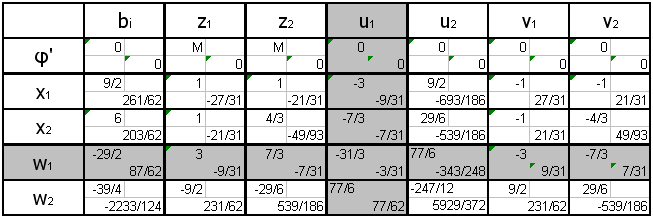
Составим симплекс-таблицу:
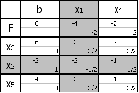
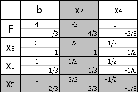

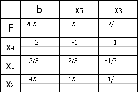
Ответ:
оптимальное решение симплекс-метода:
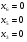
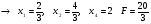
Проверка:
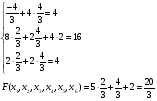
Задача 3
Условие:
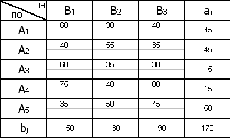
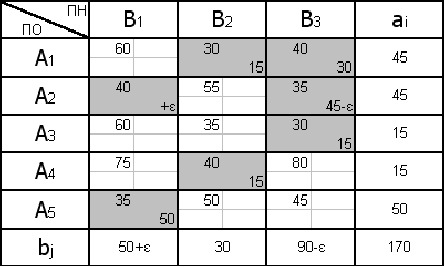
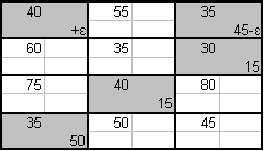
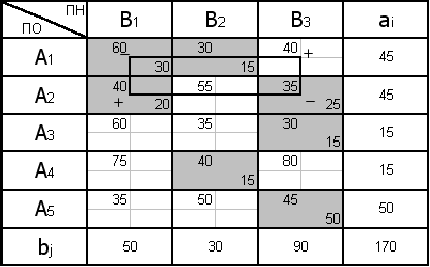
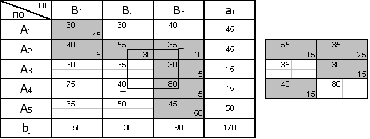
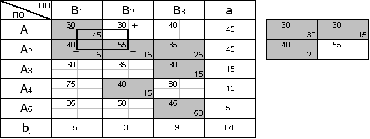
Рисунок 1 – Условие транспортной задачи
Проверка баланса:
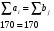 - с правильным балансом (рис. 1);
- с правильным балансом (рис. 1);
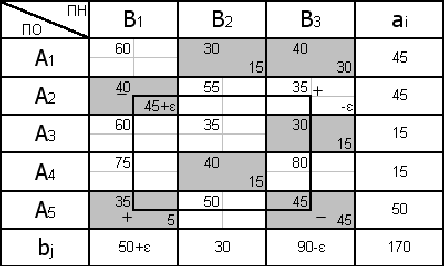
Первоначальное распределение поставок для сформулированной закрытой транспортной задачи найдем по методу «Северо-западного угла» (рис. 2).
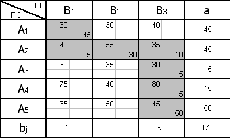
Рисунок 2 – Распределение по методу «Северо-западного угла»
Проверка является ли этот план опорным:
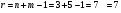
Полученное решение является опорным.
Нахождение оптимального плана, используя цикл пересчета:
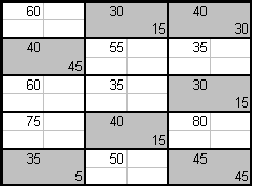
а) 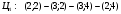
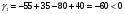
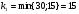
б) 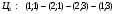
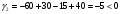
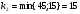
в) 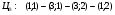
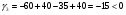
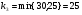
Получим:
г) 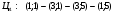
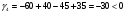
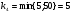
Получим:
д) 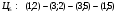
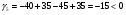
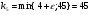
Получим:
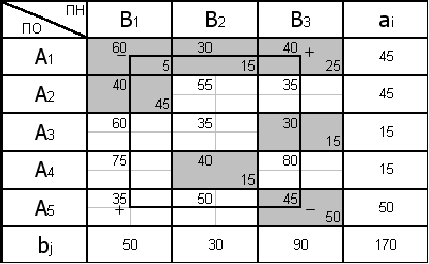
В итоге получим таблицу. Произведем проверку по методу потенциалов:
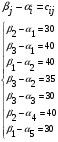
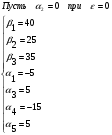
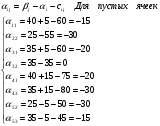
Так в системе 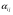 нет положительных чисел, то найденный план называется оптимальным.
нет положительных чисел, то найденный план называется оптимальным.
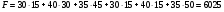
Задача 4
b1
b2
c11
c12
c22
extr
a11
a12
a21
a22
p1
p2
Знаки огр.
1
2
0
4.5
-2
3
-1.5
max
5
-2
3.5
1
25
12
≥
≤
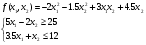
Приведем систему к стандартному виду:
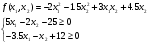
Определение стационарной точки:
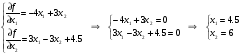
Проверка стационарной точки на относительный max или min:
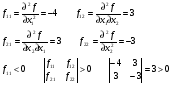
Стационарная точка является точкой относительного максимума.
Составление функции Лагранжа:
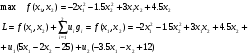
Применим теорему Куна-Таккера:
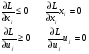
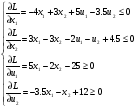 (I)
(I) 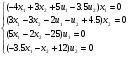 (II)
(II)
Нахождение решения системы (I):
Перепишем эту систему, оставив все переменные в левой части:
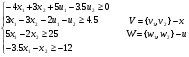
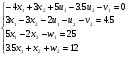
Система уравнений (II) определяет систему уравнений не жесткости:
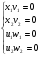 (II)’
(II)’
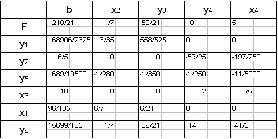
Метод искусственных переменных:
Введем искусственные переменные 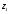 ,
,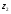 в первое и второе уравнения со знаками, совпадающими со знаками соответствующих свободных членов:
в первое и второе уравнения со знаками, совпадающими со знаками соответствующих свободных членов:
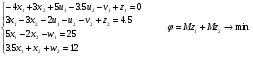
Далее решаем полученную задачу линейного программирования, для этого из 1и 2 уравнений выражаем переменные 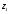 ,
,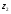 и принимаем их в качестве базисных. Из уравнения 3,4 выражаем переменные
и принимаем их в качестве базисных. Из уравнения 3,4 выражаем переменные 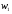 и
и 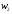 как базисные.
как базисные.
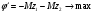
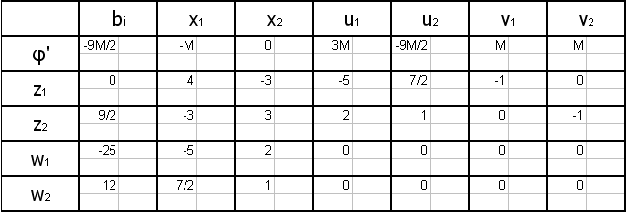
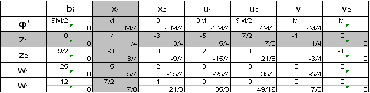
Составляем симплекс-таблицу:
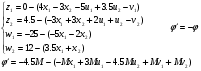

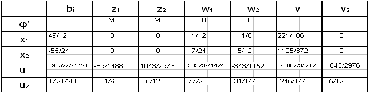
Ответ: оптимального решения квадратичного программирования не существует.
Список используемой литературы
Волков И. К., Загоруйко Е. А. Исследование операций. – Москва: Издательство МГТУ имени Баумана Н. Э., 2000г. – 436с.
Кремер Н. Ш. Исследование операций в экономике. – Москва: Издательское объединение «ЮНИТИ», 1997г. – 407с.
Курс лекций Плотникова Н.В.
Пантелеев А.В., Летова Т.А. «Методы оптимизации в примерах и задачах».

Нравится материал? Поддержи автора!
Ещё документы из категории информатика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ