Методическое пособие «Итерационные циклы. Вычисление суммы ряда»

(Колтакова Ирина Павловна, ГБОУ города Москвы «Лицей №1451»

Итерационные циклы

Существуют вычислительные процессы, которые содержат циклы с неизвестным заранее числом повторений. Такие циклы, характеризующиеся последовательным приближением вычисляемых величин к исходному значению, называются итерационными. Окончание цикла в этом случае обычно осуществляется при достижении заданной точности вычисления результата. К итерационным циклам приводят задачи вычисления сумм бесконечных рядов, реализации численных методов интегрирования, решения алгебраических и трансцендентных уравнений, решения систем уравнений, задачи оптимизации.

В итерационных процессах результаты, полученные на текущем шаге, используются в качестве исходных данных для расчета на следующем шаге цикла.

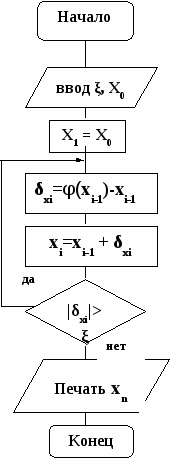
При реализации итерационного процесса на компьютере необходимо задавать начальные значения и критерий, в соответствии с которым произойдет окончание процесса. Рассмотрим сущность итерационного циклического процесса на примере решения алгебраического уравнения.

Математический метод итерации состоит в следующем. Пусть необходимо найти корень алгебраического уравнения F(x)=0. Это уравнение представляется в виде: x=φ(x).

При этом считается, что очередное приближение корня равно значение функции φ от приближения корня, полученного на предыдущем шаге: x_i=φ(x_i-1).

Если существует предел последовательности значений x_i, то можно получить искомый корень x_n.

Вычисления прекращаются, когда текущая погрешность вычислений δ_xi=x_i-x_i-1 становится по модулю меньше заданной величины ξ: |x_i-x_i-1|<ξ.

Вычислительный процесс сходится, если в интервале между приближенным значением корня x₀ и корнем уравнения x_n модуль первой производной функции φ(x) не превосходят единицу: |φ(x)|<1. Если же неравенство |φ(x)|<1 не выполняется, необходимо изменить вид уравнения x=φ(x). .

Смысл метода итерации можно пояснить и графически:

Представим левую и правую части уравнения x=φ(x) в виде двух функций Y=x и Y=φ(x). Исходя из уравнения x=φ(x) точка пересечения графиков функций Y=x и Y=φ(x) дает искомый корень уравнения ξ, который находится последовательным приближением в соответствии с формулой результат x_i=φ(x_i-1), где начальное приближение корня x=x₀ может быть найдено, например графическим построением функции f(x).

При реализации итерационного процесса обычно придерживаются следующего порядка вычислений.

Вначале находят текущую погрешность вычислений подстановкой x_i=φ(x_i-1) в δ_xi=x_i-x_i-1

δ_xi=X_i-X_i-1=φ(x_i-1)-x_i-1

Затем определяют значение нового приближения корня:

=X_i=x_i-1+δ_xi

Такой подход экономит память машины и сокращает количество операторов для реализации алгоритма. Схема данного алгоритма представлена на рисунке.

Вычисление суммы ряда

Задача сводится к нахождению суммы

S= U(1)+ U(2)+ U(3)+ … +U(n) = ∑U(n), сумма N от 1 до бесконечности.

каждое слагаемое является функцией от номера N, определяющего место этого слагаемого в сумме. А также может являться функцией одного или несколько дополнительных параметров, например:

S=1/2*3 + 2/3*4 + … + n/(n+1)(n+2) + …. = ∑n/(n+1)*(n+2),

или

S= X² /1*2 + X⁴/3*4 + … + (-1)^n-1 *X²ⁿ/(2n-1)*2n +…= ∑(-1)ⁿ⁺¹ *X²ⁿ/(2n-1)*2n,

Сумма N от 1 до бесконечности.

В общем случае начальное значение номера члена ряда N может быть отличным от 1 (например, равным 0). Обозначив его через ν, получим S = ∑U(n), сумма N от 1 до бесконечности.

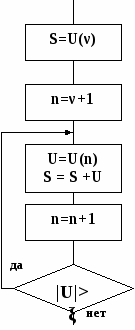
Для вычисления суммы ряда используется прием накопления суммы: суммирование считается законченным при выполнении условия достижения заданной погрешности ξ: |U(n)|≤ ξ.

Задача нахождения суммы ряда является типичным примером итерационного процесса, так как заранее не известно, при каком числе членов ряда будет достигнута требуемая точность.

Процесс вычисления определяется рекуррентным соотношением

S(n)=S(n-1)+U(n). Для определения начального значения суммы перепишем S = ∑U(n), сумма N от 1 до бесконечности, в виде: S=U(ν)+∑U(n).

Элемент U(ν) можно принять в качестве начального значения суммы, а параметр n в итерационном процессе будет принимать значения ν+1, ν+2, .

Общая схема алгоритма вычисления суммы приведена на рисунке. Поскольку в вычислениях по рекуррентной формуле одновременно участвуют лишь два значения S(n) и S(n-1), в схеме алгоритма вместо этих переменных используется переменная S. Значение S будет изменяться каждый раз при прибавлении очередного члена суммы. Справа от знака присваивания значение переменной соответствует предыдущему значению суммы S(n-1), слева – текущему S(n)

Обычно формула общего члена суммы принадлежит одному из следующих типов:

Решение: Вычисление суммы бесконечного ряда

На языке Бейсик

На языке Паскаль

Input x, eps

S=1: U=1: n=1

While abs(u) > eps

U=(-1)*u*x*x/((2*n-1)*2*n)

S=S+u

N=n+1

Wend

Print “n=”,n,”S=”,S

end

Var x, eps : real;

Begin

Read(x, eps); { ввод значений x, eps}

S:=1; U:=1; n:=1; {задание начальных значений}

While abs(u) > eps Do {проверка условия цикла}

Begin

U:=(-1)*u*x*x/((2*n-1)*2*n);{слагаемое суммы ряда}

S:=S+u; {наращивание суммы}

N:=n+1; {увеличение N на единицу}

End;

Write (‘n=’, n, ‘S=’,S); {вывод результата суммы}

End.

Задание 1. Разложение SinX ряда Тейлора без остаточного члена. Считать, что требуемая точность достигнута, если очередное слагаемое по модулю <ξ. Все последующие слагаемые можно уже не учитывать. Полученную сумму сравнивать с результатом обращения к соответствующей встроенной функции.

Решение: Вычислить с точностью ξ>0, вводимой с клавиатуры сумму ряда:

SinX=X-X³/3!+X⁵/5!–X⁷/7!+X⁹/9!-X¹¹/11! +…+ (-1)^n-1*X^(2n-1)/(2n-1)!

Var I : Integer;

y, S, x, eps : real;

Begin

Writeln(‘Введите Х=’);

Read(x); { ввод значения x}

Writeln(‘Введите eps=’);

Readln(eps); { ввод значения eps}

{*******Задание начальных значений**********}

I:=1; {задание начального значения переменной i}

Y:=X; {задание начальных значений}

S:=X; {задание начальных значений}

While abs(Y) > eps Do {проверка условия цикла (с точностью)}

Begin

i := i + 1; {увеличение i на единицу}

Y:=(-1)*Y*X*X/((2*i-2)*(2*i-1)); {слагаемое суммы ряда}

S:=S+Y; {наращивание суммы}

End;

Writeln (‘Сумма ряда=’, S:6:4); {вывод результата суммы}

Writeln (‘SinX=’, Sin(X):6:4); {вывод результата SinX}

Readln;

End.

Номера операции цикла

Выполняемые опера ции

Значения

I

Y

S

Ввести значение Х:=

Ввести значение eps := 0.0001

0 (перед циклом)

Abs(Y) > eps

I := 1

Y₀ := X

S :=X

1

I + 1 = 2

Y₁ := (-1) *(X*Х)/(2*3) *Y₀

S := S+ Y₁

2

I + 1 = 3

Y₂ := (-1) *(X*Х)/(4*5) *Y₁

S := S+ Y₂

3

I + 1 = 4

Y₃ := (-1) *(X*Х)/(6*7) *Y₂

S := S+ Y₃

…

…

…

…

…

N

I + 1 = N

Вычисление общего члена ряда:

Y_n := (-1) ^2n-1*(X*Х)/((2*I-2)*(2*I-1))*Y_n-1

S := S+ Y_n

Задание 2. Разложение CosX ряда Тейлора без остаточного члена. Считать, что требуемая точность достигнута, если очередное слагаемое по модулю <ξ. Все последующие слагаемые можно уже не учитывать. Полученную сумму сравнивать с результатом обращения к соответствующей встроенной функции.

Решение: Вычислить с точностью ξ>0, вводимой с клавиатуры сумму ряда:

CosX = 1 – X²/2! + X⁴/4! – X⁶/6! +…+ (-1)ⁿ*X⁽²ⁿ⁾/(2n)!

Var I : Integer;

y, S, x, eps : real;

Begin

Writeln(‘Введите Х=’);

Read(x); { ввод значения x}

Writeln(‘Введите eps=’);

Readln(eps); { ввод значения eps}

{*******Задание начальных значений**********}

I:=0; {задание начального значения переменной i}

Y:=1; {задание начальных значений}

S:=1; {задание начальных значений}

While abs(Y) > eps Do {проверка условия цикла (с точностью)}

Begin

i := i + 2; {увеличение i на два}

Y:=(-1)*Y*X*X/(i*(i-1)); {слагаемое суммы ряда}

S:=S+Y; {наращивание суммы}

End;

Writeln (‘Сумма ряда=’, S:6:4); {вывод результата суммы}

Writeln (‘CosX=’, Cos(X):6:4); {вывод результата SinX}

Readln; {задержка на экране}

End.

Номера операции цикла

Выполняемые опера ции

Значения

I

Y

S

Ввести значение Х:=

Ввести значение eps := 0.0001

0 (перед циклом)

Abs(Y) > eps

I := 0

Y₀ := 1

S :=1

1

I + 2 = 0+2 = 2

Y₁ := (-1) *(X*Х)/(2*1) *Y₀

S := S+ Y₁

2

I + 2 = 2+2 = 4

Y₂ := (-1) *(X*Х)/(4*3) *Y₁

S := S+ Y₂

3

I + 2= 4+2 = 6

Y₃ := (-1) *(X*Х)/(6*5) *Y₂

S := S+ Y₃

…

…

…

…

…

N

I + 1 = N

Вычисление общего члена ряда:

Y_n := (-1) ²ⁿ*(X*Х)/(I*(I-1)) *Y_n-1

S := S+ Y_n

Задание 3. Вычислить с N-ое приближение выражения

Arctg(X) = X – X²/2! + X⁴/4! – X⁶/6! +…+ (-1)ⁿX⁽²ⁿ⁾/(2n)!

Считать, что требуемая точность достигнута, если очередное слагаемое по модулю <ξ. Все последующие слагаемые можно уже не учитывать.

Решение:

Var I : Integer;

y, S, x, eps : real;

Begin

Writeln(‘Введите Х=’);

Read(x); { ввод значения x}

Writeln(‘Введите eps=’);

Readln(eps); { ввод значения eps}

{*******Задание начальных значений**********}

I:=0; {задание начального значения переменной i}

Y:=X; {задание начальных значений}

S:=0; {задание начальных значений}

While abs(Y) > eps Do {проверка условия цикла (с точностью)}

Begin

i := i + 1; {увеличение i на единицу}

Y:=(-1)*Y*X*X/(2*i-1)); {слагаемое суммы ряда}

S:=S+Y; {наращивание суммы}

End;

Writeln (‘Сумма ряда=’, S:6:4); {вывод результата суммы}

Readln; {задержка на экране}

End.

Номера операции цикла

Выполняемые опера ции

Значения

I

Y

S

Ввести значение Х:=

Ввести значение eps := 0.0001

0 (перед циклом)

Abs(Y) > eps

I := 0

Y₀ := X

S :=0

1

I + 1 = 2

Y₁ := (-1) *(X*Х)/3 *Y₀

S := S+ Y₁

2

I + 1 = 3

Y₂ := (-1) *(X*Х)/5 *Y₁

S := S+ Y₂

3

I + 1 = 4

Y₃ := (-1) *(X*Х)/7 *Y₂

S := S+ Y₃

…

…

…

…

…

N

I + 1 = N

Вычисление общего члена ряда:

Y_n := (-1) ^2n-1 *(X*Х)/(2*I-1))*Y_n-1

S := S+ Y_n