Трёхмерная компьютерная графика
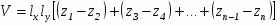
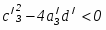
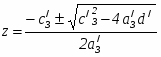
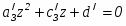
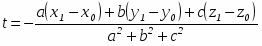
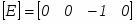
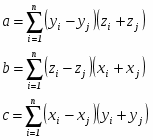
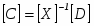
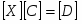
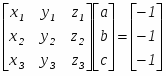
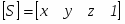
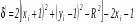
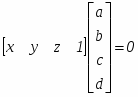

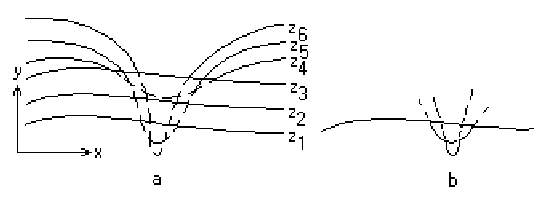
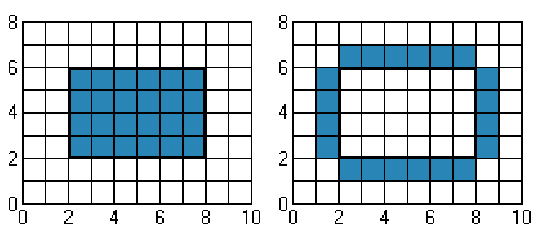
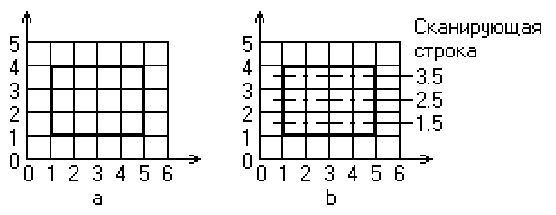
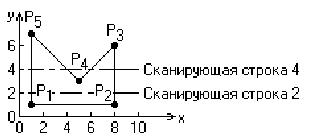
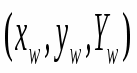
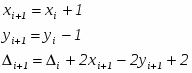
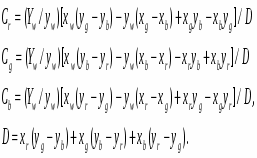
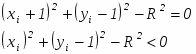
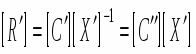
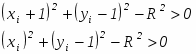
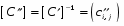
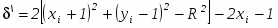
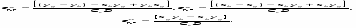
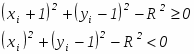
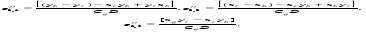
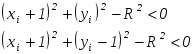
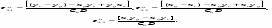
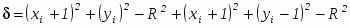
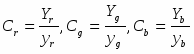
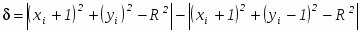
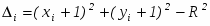
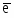
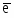
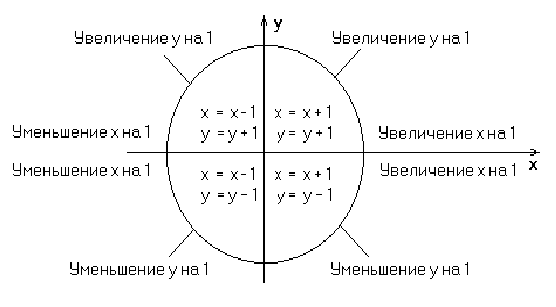
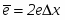
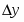
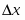
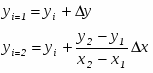
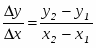
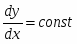 Трёхмерная компьютерная графика
Трёхмерная компьютерная графика
Введение
Машинная графика в настоящее время уже вполне сформировалась как наука. Существует аппаратное и программное обеспечение для получения разнообразных изображений - от простых чертежей до реалистичных образов естественных объектов. Машинная графика используется почти во всех научных и инженерных дисциплинах для наглядности восприятия и передачи информации. Знание её основ в наше время необходимо любому ученому или инженеру. Машинная графика властно вторгается в бизнес, медицину, рекламу, индустрию развлечений. Применение во время деловых совещаний демонстрационных слайдов, подготовленных методами машинной графики и другими средствам автоматизации конторского труда, считается нормой. В медицине становится обычным получение трехмерных изображений внутренних органов по данным компьютерных томографов. В наши дни телевидение и другие рекламные предприятия часто прибегают к услугам машинной графики и компьютерной мультипликации. Использование машинной графики в индустрии развлечений охватывает такие несхожие области как видеоигры и полнометражные художественные фильмы.
На сегодняшний день создано большое количество программ, позволяющих создавать и редактировать трёхмерные сцены и объекты. Среди наиболее популярных можно назвать такие как 3D studio Max, которая позволяет трёхмерные компьютерные ролики. Область её применения в основном реклама, мультипликация и оформление телевизионных передач. Другой не менее популярный пакет программ это Auto-CAD. Он применяется в основном инженерами и проектировщиками для создания чертежей и пространственных моделей. Кроме этих существует множество других специализированных программных пакетов охватывающих практически все стороны человеческой жизни.
Среди многообразия возможностей, предоставляемых современными вычислительными средствами, те, что основаны на пространственно-образном мышлении человека, занимают особое место. Современные программно-оперативные средства компьютерной графики представляют собой весьма эффективный инструмент поддержки такого мышления при выполнении работ самых разных видов. С другой стороны именно пространственно-образное мышление является неформальной творческой основой для расширения изобразительных возможностей компьютеров. Это важное обстоятельство предполагает взаимно обогащающее сотрудничество всё более совершенной техники и человека со всем богатством знания, накопленного предшествующими поколениями. Глаз и раньше был эффективным средством познания человеком мира и себя. Поэтому столь привлекательной оказывается компьютерная визуализация, особенно визуализация динамическая, которую следует рассматривать как важнейший инструмент для обучения наукам.
Введение в машинную графику
Современная машинная графика - это тщательно разработанная дисциплина. Обстоятельно исследованы сегменты геометрических преобразований и описаний кривых и поверхностей. Также изучены, но все еще продолжают развиваться методы растрового сканирования, отсечение, удаление линий и поверхностей, цвет, закраска, текстура и эффекты прозрачности. Сейчас наибольший интерес представляют именно эти разделы машинной графики.
Машинная графика - сложная и разнообразная дисциплина. Для изучения её, прежде всего, необходимо разбить на обозримые части. Прежде всего необходимо рассмотреть методы и алгоритмы растровой графики. Это достаточно простой, но очень важный раздел машинной графики. В этом разделе рассматриваются алгоритмы рисования отрезков и окружностей на экране монитора, методы растровой развёртки, заполнения многоугольников, устранения ступенчатости или лестничного эффекта. Отдельно следует рассмотреть методы отсечения изображения, т.е. отбора той информации, которая необходима для визуализации конкретной сцены.
При построении трёхмерной сцены возникает проблема удаления невидимых линий и поверхностей. Это одна из наиболее сложных составляющих визуализации трёхмерных объектов. Способы достижения эффектов прозрачности, отражения и т.п., строго говоря, не входят в задачу удаления невидимых частей трёхмерных объектов и, тем не менее, некоторые из них тесно связаны с этой проблемой. Например, построение теней. Не смотря на это, в компьютерной графике выделяется довольно большой раздел, посвящённый построению реалистичных изображений, в котором подробно рассматриваются методы создания таких эффектов как зеркальное отражение, преломление лучей в различных средах, тени, фактура объекта. Так же рассматриваются различные источники света, их спектральные характеристики и форма. Сюда же относятся цветовые эффекты, сглаживание поверхностей и многое другое.
Как видно из выше сказанного компьютерная графика это достаточно объемная дисциплина, поэтому я остановлюсь лишь на некоторых её наиболее интересных аспектах.
Растровая графика
Любое изображение, в том числе и трёхмерное, состоит из графических примитивов. Поэтому, прежде всего, необходимо знать специальные методы генерации изображения, вычерчивание прямых и кривых линий, закраски многоугольников, создающей впечатление сплошных объектов. Рассмотрим некоторые из этих методов.
Алгоритмы вычерчивания отрезков
Поскольку экран дисплея можно рассматривать как матрицу дискретных элементов (пикселов), каждый из которых может быть подсвечен, нельзя непосредственно провести отрезок из одной точки в другую. Процесс определения пикселов, наилучшим образом аппроксимирующих заданный отрезок, называется разложением в растр. Для горизонтальных, вертикальных и наклоненных под углом 45 отрезков выбор растровых элементов очевиден. При любой другой ориентации выбрать нужные пикселы труднее.
Существует несколько алгоритмов выполняющих эту задачу. Рассмотрим два из них.
Цифровой дифференциальный анализатор
Один из методов разложения отрезка в растр состоит в решении дифференциального уравнения, описывающего этот процесс. Для прямой линии имеем:
или н
Решение представляется в виде
(2.1. (2.1.)
где x1, y1 и x2, y2 – концы разлагаемого отрезка и yi – начальное значение для очередного шага вдоль отрезка. Фактически уравнение (2.1.) представляет собой рекуррентное соотношение для последовательных значений y вдоль нужного отрезка. Этот метод, используемый для разложения в растр отрезков, называется цифровым дифференциальным анализатором (ЦДА). В простом ЦДА либо , либо (большее из приращений) выбирается в качестве единицы растра. Ниже приводится простой алгоритм, работающий во всех квадрантах:
Процедура разложения в растр отрезка по методу цифрового дифференциального анализатора (ЦДА)
предполагается, что концы отрезка (x1,y1) и (x2,y2) не совпадают
Integer – функция преобразования вещественного числа в целое.
Примечание: во многих реализациях функция Integer означает взятие целой части, т.е. Integer( 8.5) = 9, а не 8. В алгоритме используется именно такая функция.
Sign функция, возвращающая 1, 0, 1 для отрицательного нулевого и положительного аргумента соответственно.
if abs ( x2 x1 ) abs ( y2 y1 ) then
Длина = abs ( x2 x1 )
else
Длина = abs ( y2 y1 )
end if
полагаем большее из приращений x или y равным единице растра
x = ( x2 x1 ) / Длина
y = ( y2 y1 ) / Длина
округляем величины, а не отбрасываем дробную часть
использование знаковой функции делает алгоритм пригодным для всех квадрантов
x = x1 + 0.5 * Sign ( x )
y = y1 + 0.5 * Sign ( y )
начало основного цикла
i =1
while ( i Длина )
Plot ( Integer ( x ), Integer ( y ) )
x = x + x
y = y + y
i = i + 1
end while
finish
С помощью этого алгоритма получают прямые, вполне удовлетворительного вида, но у него есть ряд недостатков. Во-первых, плохая точность в концевых точках. Во-вторых, результаты работы алгоритма зависят от ориентации отрезка. Вдобавок предложенный алгоритм использует вещественную арифметику, что заметно снижает скорость выполнения.
Алгоритм Брезенхема
Алгоритм Брезенхема выбирает оптимальные растровые координаты для представления отрезка. В процессе работы одна из координат - либо x, либо у (в зависимости от углового коэффициента) - изменяется на единицу. Изменение другой координаты (либо на нуль, либо на единицу) зависит от расстояния между действительным положением отрезка и ближайшими координатами сетки. Такое расстояние называется ошибкой.
Алгоритм построен так, что требуется проверять лишь знак этой ошибки. На рис.2.1 это иллюстрируется для отрезка в первом
½ y 1 (ошибка 0)
0 y/x < ½ (ошибка <0)
Инициировать ошибку в – ½
ошибка = ошибка + y/x
2.1 Основная идея алгоритма Брезенхема
октанте, т. е. для отрезка с угловым коэффициентом, лежащим в диапазоне от нуля до единицы. Из рисунка можно заметить, что если угловой коэффициент отрезка из точки (0,0) больше чем 1/2, то его пересечение с прямой x = 1 будет расположено ближе к прямой у = 1, чем к прямой у = 0. Следовательно, точка растра (1,1) лучше аппроксимирует ход отрезка, чем точка (1,0). Если угловой коэффициент меньше 1/2, то верно обратное. Для углового коэффициента равного 1/2 нет какого-либо предпочтительного выбора. В данном случае алгоритм выбирает точку (1,1).
Быстродействие алгоритма можно существенно увеличить, если использовать только целочисленную арифметику и исключить деление. Т.к. важен лишь знак ошибки, то приняв
можно добиться хорошей скорости выполнения алгоритма.
2.2 Разбор случаев для обобщённого алгоритма Брезенхема.
Чтобы реализация алгоритма была полной необходимо обрабатывать отрезки во всех октантах. Когда абсолютная величина углового коэффициента больше 1, y постоянно изменяется на единицу, а критерий ошибки Брезенхема используется для принятия решения об изменении величены x. Выбор постоянно изменяющейся (на +1 или –1) координаты зависит от квадранта (рис. 2.2).
Алгоритм Брезенхема может быть оформлен в следующем виде.
Обобщённый целочисленный алгоритм Брезенхема квадрантов
предполагается, что концы отрезка (x1,y1) и (x2,y2) не совпадают и все переменные целые.
Функция Sign возвращает 1, 0, 1 для отрицательного нулевого и положительного аргумента соответственно.
инициализация переменных
x = x1
y = y1
x = abs ( x2 x1 )
y = abs ( y2 y1 )
s1 = Sign ( x2 x1 )
s2 = Sign ( y2 y1 )
обмен значение x и y в зависимости от углового коэффициента наклона отрезка
if y > x then
Врем = x
x = y
y = Врем
Обмен = 1
else
Обмен = 0
end if
инициализация с поправкой на половину пиксела
= 2 * y x
основной цикл
for i = 1 to x
Plot ( x ,y )
While ( 0 )
If Обмен = 1 then
x = x + s1
else
y = y + s2
end if
= 2 * x
end while
if Обмен = 1 then
y = y + s2
else
x = x + s1
end if
= + 2 * y
next i
finish
Этот алгоритм удовлетворяет самым строгим требованиям. Он имеет приемлемую скорость и может быть легко реализован на аппаратном или микропрограммном уровне.
Алгоритм Брезенхема для генерации окружностей
В растр нужно разлагать не только линейные, но и другие, более сложные функции. Разложению конических сечений, т. е. окружностей, эллипсов, парабол, гипербол посвящено значительное число работ. Наибольшее внимание, разумеется, уделено окружности. Один из наиболее эффективных и простых для понимания алгоритмов генерации окружности принадлежит
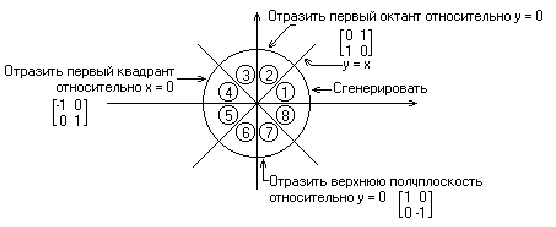
2.3 Генерация полной окружности из дуги в первом октанте
Брезенхему. Для начала заметим, что необходимо сгенерировать только одну восьмую часть окружности. Остальные её части могут быть получены последовательными отражениями, как это показано на рис. 2.3. Если сгенерирован первый октант (от 0 до 45 против часовой стрелки), то второй октант можно получить зеркальным отражением относительно прямой у = x, что дает в совокупности первый квадрант. Первый квадрант отражается относительно прямой x = 0 для получения соответствующей части окружности во втором квадранте. Верхняя полуокружность отражается относительно прямой у = 0 для завершения построения. На рис.2.3. приведены двумерные матрицы соответствующих преобразований.
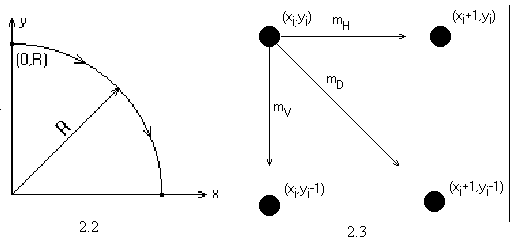
Для вывода алгоритма рассмотрим первую четверть окружности с центром в начале координат. Заметим, что если работа алгоритма начинается в точке x = 0, у = R, то при генерации окружности по часовой стрелке в первом квадранте у является монотонно убывающей функцией аргумента x (рис. 2.4). Аналогично, если исходной точкой является y = 0, x = R, то при генерации окружности против часовой стрелки x будет монотонно убывающей функцией аргумента у. В нашем случае выбирается генерация по часовой стрелке с началом в точке x = 0, у = R. Предполагается, что центр окружности и начальная точка находятся точно в точках растра.
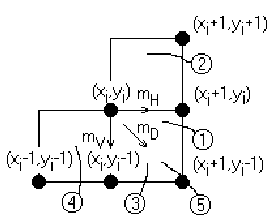
Для любой заданной точки на окружности при генерации по часовой стрелке существует только три возможности выбрать следующий пиксел, наилучшим образом приближающий окружность: горизонтально вправо, по диагонали вниз и вправо, вертикально вниз. На рис.2.5 эти направления обозначены соответственно mH, mD, mV.
2.4 Окружность в первом квадранте. 2.5 Выбор пикселов в первом квадранте
Алгоритм выбирает пиксел, для которого минимален квадрат расстояния между одним из этих пикселов и окружностью, т. е. минимум из
mH = | ( xi + 1 )2 + ( yi )2 – R2 |
mH = | ( xi + 1 )2 + ( yi 1 )2 – R2 |
mH = | ( xi )2 + ( yi 1 )2 – R2 |
Вычисления можно упростить, если заметить, что в окрестности точки ( xi, yi ) возможны только пять типов пересечений окружности и сетки растра, приведенных на рис.2.6.
Разность между квадратами расстояний от центра окружности до диагонального пиксела ( xi + 1, yi 1 ) и от центра до точки на окружности R2 равна
Как и в алгоритме Брезенхема для отрезка, для выбора соответствующего пиксела желательно использовать только знак ошибки, а не её величину.
2.6 Пересечение окружности и сетки растра
При < 0 диагональная точка ( xi + 1, yi 1 ) находится внутри реальной окружности, т. е. это случаи 1 или 2 на рис.2.6. Ясно, что в этой ситуации следует выбрать либо пиксел ( xi + 1, yi ) т. е. mH, либо пиксел ( xi + 1, yi 1 ), т. е. mD. Для этого сначала рассмотрим случай 1 и проверим разность квадратов расстояний от окружности до пикселов в горизонтальном и диагональном направлениях:
При < 0 расстояние от окружности до диагонального пиксела
(mD) больше, чем до горизонтального (mH). Напротив, если > 0, расстояние до горизонтального пиксела (mH) больше. Таким образом,
при < 0 выбираем mH ( xi + 1, уi )
при > 0 выбираем mD ( xi + 1, уi – 1 )
При = 0, когда расстояния от окружности до обоих пикселов одинаковы, выбираем горизонтальный шаг.
Количество вычислений, необходимых для оценки величины , можно сократить, если заметить, что в случае 1
так как диагональный пиксел ( xi + 1, уi – 1 ) всегда лежит внутри окружности, а горизонтальный ( xi + 1, уi ) - вне ее. Таким образом, можно вычислить по формуле
Дополнение до полного квадрата члена ( yi )2 с помощью добавления и вычитания - 2уi + 1 дает
В квадратных скобках стоит по определению i, и его подстановка
= 2(i + yi) – 1
существенно упрощает выражение.
Рассмотрим случай 2 на рис.2.6 и заметим, что здесь должен быть выбран горизонтальный пиксел ( xi + 1, уi ), так как у является монотонно убывающей функцией. Проверка компонент показывает, что
поскольку в случае 2 горизонтальный ( xi + 1, уi ) и диагональный ( xi + 1, уi – 1 ) пикселы лежат внутри окружности. Следовательно, < 0, и при использовании того же самого критерия, что и в случае 1, выбирается пиксел ( xi + 1, уi ).
Если i > 0, то диагональная точка ( xi + 1, уi – 1 ) находится вне окружности, т. е. это случаи З и 4 на рис.2.6. В данной ситуации ясно, что должен быть выбран либо пиксел ( xi + 1, уi – 1 ), т. е. mD, либо ( xi, уi – 1 ), т. е. mV. Аналогично разбору предыдущего случая критерий выбора можно получить, рассматривая сначала случай З и проверяя разность между квадратами расстояний от окружности до диагонального mD и вертикального mV пикселов, т. е.
При \ < 0 расстояние от окружности до вертикального пиксела ( xi, уi – 1 ) больше и следует выбрать диагональный шаг mD, к пикселу ( xi + 1, уi – 1 ). Напротив, в случае \ > 0 расстояние от окружности до диагонального пиксела больше и следует выбрать вертикальное движение к пикселу ( xi, уi – 1 ). Таким образом,
при 0 выбираем mD в ( xi + 1, уi – 1 )
при < 0 выбираем mV в ( xi, уi – 1 )
Здесь в случае = 0, т. е. когда расстояния равны, выбран диагональный шаг.
Проверка компонент \ показывает, что
поскольку для случая З диагональный пиксел ( xi + 1, уi – 1 ) находится вне окружности, тогда как вертикальный пиксел ( xi, уi – 1 ) лежит внутри ее. Это позволяет записать \ в виде
Дополнение до полного квадрата члена ( xi )2 с помощью добавления и вычитания 2xi + 1 дает
Использование определения i приводит выражение к виду
Теперь, рассматривая случай 4, снова заметим, что следует выбрать вертикальный пиксел ( xi, уi – 1 ), так как y является монотонно убывающей функцией при возрастании x. проверка компонент \ для случая 4 показывает, что
поскольку оба пиксела находятся вне окружности. Следовательно, \ > 0 и при использовании критерия, разработанного для случая 3, происходит верный выбор mV.
Осталось проверить только случай 5 на рис.2.7, который встречается, когда диагональный пиксел ( xi + 1, уi – 1 ) лежит на окружности, т. е. i = 0. Проверка компонент показывает, что
Следовательно, > 0 и выбирается диагональный пиксел ( xi + 1, уi – 1 ). Аналогичным образом оцениваем компоненты \:
и < 0, что является условием выбора правильного диагонального шага к ( хi + 1, уi – 1 ). Таким образом, случай i = 0 подчиняется тому же критерию, что и случай i < 0 или i > 0.
Подведем итог полученных результатов:
i < 0
0 выбираем пиксел ( хi + 1, уi ) mH
> 0 выбираем пиксел ( хi + 1, уi – 1 ) mD
i > 0
\ 0 выбираем пиксел ( хi + 1, уi – 1 ) mD
\ > 0 выбираем пиксел ( хi , уi – 1 ) mV
i = 0 выбираем пиксел ( хi + 1, уi – 1 ) mD
Легко разработать простые рекуррентные соотношения дня реализации пошагового алгоритма. Сначала рассмотрим горизонтальный шаг mH к пикселу ( хi + 1, уi ). Обозначим это новое положение пиксела как ( i + 1 ). Тогда координаты нового пиксела и значение i равны
Аналогично координаты нового пиксела и значения i для шага mD к пикселу ( хi + 1, уi – 1 ) таковы:
То же самое для шага mV к ( хi, уi – 1 )
Реализация алгоритма Брезенхема для окружности приводиться ниже.
Пошаговый алгоритм Брезенхема для генерации окружности в первом квадранте
все переменные целые
xi = 0
yi = R
i = 2(1 – R)
Предел = 0
Plot ( xi, yi )
if yi Предел then 4
выделение случая 1 или 2, 4 или 5, или 3
if i < 0 then 2
if i > 0 then 3
if i = 0 then 20
определение случая 1 или 2
= 2i + 2yi – 1
if 0 then 10
if > 0 then 20
определение случая 4 или 5
= 2i + 2xi – 1
if 0 then 20
if > 0 then 30
выполнение шагов
шаг mH
xi = xi +1
i = i +2xi + 1
goto 1
шаг mD
xi = xi +1
yi = yi – 1
i = i +2xi – 2yi + 2
goto 1
шаг mV
30yi = yi – 1
i = i – 2xi + 1
goto 1
4finish
Растровая развёртка сплошных областей
До сих пор речь шла о представлении на растровом графическом устройстве отрезков прямых линий. Однако одной из уникальных характеристик такого устройства является возможность представления сплошных областей. Генерацию сплошных областей из простых описаний ребер или вершин будем называть растровой разверткой сплошных областей, заполнением многоугольников или заполнением контуров. Для этого можно использовать несколько методов, которые обычно делятся на две широкие категории: растровая развертка и затравочное заполнение.
В методах растровой развертки пытаются определить в порядке
сканирования строк, лежит ли точка внутри многоугольника или контура. Эти алгоритмы обычно иду от “верха” многоугольника или контура к “низу”.
В методах затравочного заполнения предполагается, что известна некоторая точка (затравка) внутри замкнутого контура. В алгоритмах ищут точки, соседние с затравочной и расположенные внутри контура. Если соседняя точка расположена не внутри, значит, обнаружена граница контура. Если же точка оказалась внутри контура, то она становится новой затравочной точкой и поиск продолжается рекурсивно.
Растровая развёртка многоугольников
Можно разработать эффективный метод растровой развёртки многоугольников, если воспользоваться тем фактом, что соседние пикселы, вероятно, имеют одинаковые характеристики (кроме пикселов граничных рёбер). Это свойство называется пространственной когерентностью.
2.7 Растровая развёртка сплошной области
Характеристики пикселов на данной строке изменяются только там, где ребро многоугольника пересекает строку. Эти пересечения делят сканирующую строку на области.
Для простого многоугольника на рис. 2.7 строка 2 пересекает многоугольник при x = 1 и x = 8.
Получаем три области:
x < 1вне многоугольника
1 x 8внутри многоугольника
x > 8вне многоугольника
Строка 4 делится на пять областей:
x < 1вне многоугольника
1 x 4внутри многоугольника
4 < x < бвне многоугольника
б x 8внутри многоугольника
x > 8вне многоугольника
Совсем необязательно, чтобы точки пересечения для строки 4 сразу определялись в фиксированном порядке (слева направо). Например, если многоугольник задаётся списком вершин P1, P2, P3, P4, а список рёбер последовательными парами вершин P1P2, P2P3, P3P4, P4P5, P5P1, то для строки 4 будут найдены следующие точки пересечения с рёбрами многоугольника: 8, 6, 4, 1. Эти точки надо отсортировать в возрастающем порядке по x, т. е. получить 1,4, 6, 8.
При определении интенсивности, цвета и оттенка пикселов на сканирующей строке рассматриваются пары отсортированных точек пересечений. Для каждого интервала, задаваемого парой пересечений, используется интенсивность или цвет заполняемого многоугольника. Для интервалов между парами пересечений и крайних (от начала строки до первой точки пересечения и от последней точки пересечения до конца строки) используется фоновая интенсивность или цвет.
2.8 Системы координаты строк сканирования.
Точное определение тех пикселов, которые должны активироваться, требует некоторой осторожности. Рассмотрим простой прямоугольник, изображенный на рис. 2.8. Прямоугольник имеет координаты (1,1), (5,1), (5,4), (1,4). Сканирующие строки с 1 по 4 имеют пересечения с ребрами многоугольника при x = 1 и 5. Пиксел адресуется координатами своего левого нижнего угла, значит, для каждой из этих сканирующих строк будут активированы пикселы с x-координатами 1, 2, 3, 4 и 5. На рис. 2.8 показан результат. Заметим, что площадь, покрываемая активированными пикселами, равна 20, в то время как настоящая площадь прямоугольника равна 12.
Модификация системы координат сканирующей строки и теста активации устраняет эту проблему, как это показано на рис. 2.8,b. Считается, что сканирующие строки проходят через центр строк пикселов, т. е. через середину интервала, как это показано на рис. 2.8,b. Тест активации модифицируется следующим образом: проверяется, лежит ли внутри интервала центр пиксела, расположенного справа от пересечения. Однако пикселы все еще адресуются координатами левого нижнего угла. Как показано на рис.2.8,b, результат данного метода корректен.
Горизонтальные ребра не могут пересекать сканирующую строку и, таким образом, игнорируются. Это совсем не означает, что их нет на рисунке. Эти ребра формируются верхней и нижней строками пикселов.
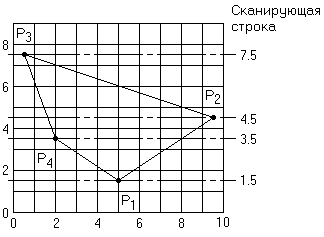
Дополнительная трудность возникает при пересечении сканирующей строки и многоугольника точно по вершине, как это показано на рис. 2.9. При использовании соглашения о середине интервала между сканирующими строками получаем, что строка у = 3.5 пересечет многоугольник в 2, 2 и 8, т. е. получится нечетное количество пересечений. Следовательно, разбиение пикселов на пары даст неверный результат, т. е. пикселы (0,3), (1,3) и от (3,3) до (7,3) будут фоновыми, а пикселы (2,3), (8,3), (9,3) окрасятся в цвет многоугольника. Если учитывать только одну точку пересечения с вершиной. Тогда для строки у = 3.5 получим правильный результат. Однако результат применения метода к строке у = 1.5, имеющей два пересечения в (5,1), показывает, что метод неверен. Для этой строки именно разбиение на пары даст верный результат, т. е. окрашен будет только пиксел (5,1). Если же учитывать в вершине только одно пересечение, то пикселы от (0,1) до (4,1) будут фоновыми, а пикселы от (5,1) до (9,1) будут окрашены в цвет многоугольника.
2.9 Особенности пересечения со строками сканирования.
Правильныйрезультат можно получить, учитывая точку пересечения в вершине два реза, если она является точкой локального минимума или максимума и учитывая один раз в противном случае. Определить локальный максимум или минимум многоугольника в рассматриваемой вершине можно с помощью проверки концевых точек двух ребер. Если у обоих рёбер у больше, чем у вершины, значит, вершина является точкой локального минимума. Если меньше, значит, вершина - точка локального максимума. Если одна больше, а другая меньше, следовательно, вершина не является ни точкой локального минимума, ни точкой локального максимума. На рис.2.10 точка Р1 - локальный минимум, Р3 - локальный максимум, а Р2, Р4 - ни то ни другое. Следовательно, в точках Р1 и Р3 учитываются два пересечения со сканирующими
строками, а в Р2 и Р4 - одно.
Алгоритм с упорядоченным списком рёбер
Используя описанные выше методы, можно разработать эффективные алгоритмы растровой развертки сплошных областей, называемые алгоритмами с упорядоченным списком ребер. Эффективность этих алгоритмов зависит от эффективности сортировки. Приведём очень простой алгоритм.
Алгоритм с упорядоченным списком ребер, использующий список активных рёбер.
Подготовить данные:
Используя сканирующие строки, проведенные через середины отрезков, т. е. через у + ½ определить для каждого ребра многоугольника наивысшую сканирующую строку, пересекаемую ребром.
Занести ребро многоугольника в у- группу, соответствующую этой сканирующей строке.
Сохранить в связном списке значения: начальное значение координат x точек пересечения, y - число сканирующих строк, пересекаемых ребром многоугольника, и ~ x – шаг приращения по x при переходе от одной сканирующей строки к другой.
Преобразовать эти данные в растровую форму:
Для каждой сканирующей строки проверить соответствующую у- группу на наличие новых ребер. Новые ребра добавить в список активных рёбер.
Отсортировать координаты x точек пересечения из САР в порядке возрастания; т. е. х1 предшествует x2, если х1 < х2
Выделить пары точек пересечений из отсортированного по
x списка. Активировать на сканирующей строке y пикселы для целых значений x, таких, что x1 x + ½ x2. Для каждого ребра из САР уменьшить у на 1. Если у < 0, то исключить данное ребро из САР. Вычислить новое значение координат x точек пересечения xнов = xстар + x
Перейти к следующей сканирующей строке
В алгоритме предполагается, что все данные предварительно преобразованы в представление, принятое для многоугольников.
Алгоритм заполнения по рёбрам
Алгоритм, использующий список ребер и флаг, является двух шаговым. Первый шаг состоит в обрисовке контура, в результате чего на каждой сканирующей строке образуются пары ограничивающих пикселов. Второй шаг состоит в заполнении пикселов, расположенных между ограничивающими. Более точно алгоритм можно сформулировать в следующем виде:
Алгоритм со списком ребер и флагом
Обрисовка контура:
Используя соглашения о середине интервала между сканирующими строками для каждого ребра, пересекающего сканирующую строку, отметить самый левый пиксел, центр которого лежит справа от пересечения; т.е.
x + 1/2 > xпересечения
Заполнение:
Для каждой сканирующей строки, пересекающей многоугольник
Внутри = FALSE
for x = 0 (левая граница) to x = xmax, (правая граница)
if пиксел в точке x имеет граничное значение
then инвертировать значение переменной Внутри
if Внутри = TRUE then
присвоить пикселу в x значение цвета многоугольника
else
присвоить пикселу в x значение цвета фона
end if
next x
В данном алгоритме каждый пиксел обрабатывается только один раз, так что затраты на ввод/вывод значительно меньше, чем в алгоритме со списком рёбер, в результате чего, при его аппаратной реализации, он работает на один-два порядка быстрее чем алгоритм с упорядоченным списком рёбер.
Алгоритмы заполнения с затравкой
В обсуждавшихся выше алгоритмах заполнение происходит в порядке сканирования. Иной подход используется в алгоритмах заполнения с затравкой. В них предполагается, что известен хотя бы один пиксел из внутренней области многоугольника. Алгоритм пытается найти и закрасить все другие пикселы, принадлежащие внутренней области. Области могут быть либо внутренние, либо гранично-определенные.
Рис. 2.10. Внутренне - определённая область
Рис. 2.11. Гранично-определённая область
Если область относится к внутренне - определенным, то все пикселы, принадлежащие внутренней части, имеют один и тот же цвет или интенсивность, а все пикселы, внешние по отношению к области, имеют другой цвет. Это продемонстрировано на рис. 2.10. Если область относится к гранично-определенным, то все пикселы на границе области имеют выделенное значение или цвет, как это показано на рис. 2.11. Алгоритмы, заполняющие внутренне - определенные области, называются внутренне - заполняющими, а алгоритмы для гранично-определённых областей – гранично-заполняющими. Далее будут обсуждаться гранично-заполняющие алгоритмы, однако соответствующие внутренне заполняющие алгоритмы можно получить аналогичным образом.
Внутренне- или гранично-определённые области могут быть 4- или 8- связными. Если область 4-связная, то любой пиксел в области можно достичь с помощью комбинаций движений только в 4-х направлениях: налево, направо, вверх, вниз. Для 8-и связной области добавляются ещё и диагональные направления. Алгоритм заполнения 8-связной области заполнит и 4-связную, но обратное не верно. Однако в ситуации, когда требуется заполнить разными цветами две отдельные 4-связные области, использование 8-связного алгоритма даст не верный результат. Далее речь пойдёт об алгоритмах для 4-связных областей, однако их легко адаптировать и для 8-связных.
Построчный алгоритм заполнения с затравкой
Используя стек, можно разработать алгоритм заполнения гранично-определенной области. Стек - это просто массив или другая структура данных, в которую можно последовательно помещать значения и из которой их можно последовательно извлекать. Как показывает практика, стек может быть довольно большим. Зачастую в нём содержится дублирующаяся информация. В построчном алгоритме заполнения с затравкой стек минимизируется за счёт хранения только затравочного пиксела для любого непрерывного интервала на сканирующей строке. Непрерывный интервал - это группа примыкающих друг к другу пикселов (ограниченная уже заполненными или граничными пикселами). Мы для разработки алгоритма используем эвристический подход, однако также возможен и теоретический подход, основанный на теории графов.
Данный алгоритм применим гранично-определённым 4-связным областям, которые могут быть как выпуклыми, так и не выпуклыми, а также могут содержать дыры. В области, внешней и примыкающей к нашей, не должно быть пикселов с цветом, которым область или многоугольник заполнятся. Схематично работу алгоритма можно разбить на четыре этапа.
Построчный алгоритм заполнения с затравкой
Затравочный пиксел на интервале извлекается из стека, содержащего затравочные пикселы.
Интервал с затравочным пикселом заполняется влево и вправо от затравки вдоль сканирующей строки до тех пор пока не будет найдена граница.
В переменной Xлев и Xправ запоминаются крайний левый и крайний правый пикселы интервала
В диапазоне Xлев x Xправ проверяются строки расположенные непосредственно над в под текущей строкой. Определяется, есть ли на них еще не заполненные пикселы. Если такие пикселы есть (т. е. не все пикселы граничные, или уже заполненные), то в указанном диапазоне крайний правый пиксел в каждом интервале отмечается как затравочный и помещается в стек.
При инициализации алгоритма в стек помешается единственный затравочный пиксел, работа завершается при опустошении стека. Ниже приводится более подробное описание алгоритма на псевдокоде.
Построчный алгоритм заполнения с затравкой
Затравка ( x, y ) выдаёт затравочный пиксел
Pop -процедура, которая извлекает пиксел из стека
Push - процедура, которая помещает пиксел в стек
инициируем стек
Push Затравка ( x, y )
While ( стек не пуст )
Извлекаем пиксел из стека и присваиваем ему новое значениеPop Пиксел ( x, y )
Пиксел ( x, y ) = Нов_значение
сохраняем x- координату затравочного пиксела
Врем_х = x
заполняем интервал справа от затравки
x = x +1
while Пиксел ( x, y ) Гран_значение
Пиксел ( x, y ) = Нов_значение
x = x +1
end while
сохраняем крайний справа пиксел
Xправ = x 1
восстанавливаем x- координату затравки
x = Врем_х
заполняем интервал слева от затравки
x = x 1
while Пиксел ( x, y ) Гран_значение
Пиксел ( x, y ) = Нов_значение
x = x 1
end while
сохраняем крайний слева пиксел
Xлев = x +1
восстанавливаем x- координату затравки
x = Врем_х
проверим, что строка выше не является ни границей многоугольника, ни уже полностью заполненной; если это не так, то найти затравку, начиная с левого края подинтервала сканирующей строки
x = Xлев
y = y +1
while x Xправ
ищем затравку на строке выше
Флаг = 0
while ( Пиксел ( x, y ) Гран_значение and
Пиксел ( x, y ) Нов_значение and x < Xправ )
if Флаг = 0 then Флаг = 1
x = x + 1
end while
помещаем в стек крайний справа пиксел
if Флаг =1 then
if ( x = Xправ and Пиксел ( x, y ) Гран_значение and Пиксел ( x, y ) Нов_значение ) then
Push Пиксел ( x, y )
else
Push Пиксел ( x 1, y )
end if
Флаг = 0
end if
продолжим проверку, если интервал был прерван
Xвход = x
while (( Пиксел ( x, y ) = Гран_значение or
Пиксел ( x, y ) = Нов_значение ) and x < Xправ)
x = x + 1
end while
удостоверимся что координата пиксела увеличена
if x = Xвход then x = x + 1
end while
проверим, что строка ниже не является ни границей многоугольника, ни уже полностью заполненной
Эта часть алгоритма совершенно аналогична проверке для строки выше, за исключением, того что вместо y = y + 1 надо подставить y = y 1
end while
finish
Удаление невидимых линий и поверхностей
Задача удаления невидимых линий и поверхностей является одной из наиболее сложных в машинной графике. Алгоритмы удаления невидимых линий и поверхностей служат для определения линий ребер, поверхностей или объемов, которые видимы или невидимы для наблюдателя, находящегося в заданной точке пространства.
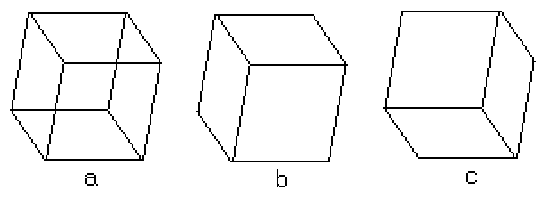
3.1 Необходимость удаления невидимых линий
Необходимость удаления невидимых линий, ребер, поверхностей или объемов проиллюстрирована рис.3.1. На рис.3.1, а приведен типичный каркасный чертеж куба. Его можно интерпретировать двояко: как вид куба сверху, слева или снизу, справа. Удаление тех линий или поверхностей, которые невидимы с соответствующей точки зрения, позволяют избавиться от неоднозначности. Результаты показаны на рис.3.1, b и c.
Сложность задачи удаления невидимых линий и поверхностей привела к появлению большого числа, различных способов ее решения. Многие из них ориентированы на специализированные приложения. Наилучшего решения общей задачи удаления невидимых линий и поверхностей не существует. Для моделирования процессов в реальном времени, например, для авиа тренажеров, требуются быстрые алгоритмы, которые могут порождать результаты с частотой видео генерации (30 кадр/с). Для машинной мультипликации требуются алгоритмы, которые могут генерировать сложные реалистические изображения, в которых представлены тени, прозрачность и фактура, учитывающие эффекты отражения и преломления цвета в мельчайших оттенках. Подобные алгоритмы работают медленно, и зачастую на вычисления требуется несколько минут или даже часов. Строго говоря, учет эффектов прозрачности, фактуры, отражения и т. п. не входит в задачу удаления невидимых линий или поверхностей. Естественнее считать их частью процесса визуализации изображения. Процесс визуализации является интерпретацией или представлением изображения или сцены в реалистической манере. Однако многие из этих эффектов встроены в алгоритмы удаления невидимых поверхностей и поэтому будут затронуты. Существует тесная взаимосвязь между скоростью работы алгоритма и детальностью его результата. Ни один из алгоритмов не может достигнуть хороших оценок для этих двух показателей одновременно. По мере создания все более быстрых алгоритмов можно строить все более детальные изображения. Реальные задачи, однако, всегда будут требовать учета еще большего количества деталей.
Алгоритмы удаления невидимых линий или поверхностей можно классифицировать по способу выбора системы координат или пространства, в котором они работают. Алгоритмы, работающие в объектном пространстве, имеют дело с физической системой координат, в которой описаны эти объекты. При этом получаются весьма точные результаты, ограниченные, вообще говоря, лишь точностью вычислений. Полученные изображения можно свободно увеличивать во много раз. Алгоритмы, работающие в объектном пространстве, особенно полезны в тех приложениях, где необходима высокая точность. Алгоритмы же, работающие в пространстве изображения, имеют дело с системой координат того экрана, на котором объекты визуализируются. При этом точность вычислений ограничена разрешающей способностью экрана. Результаты, полученные в пространстве изображения, а затем увеличенные во много раз, не будут соответствовать исходной сцене. Алгоритмы, формирующие список приоритетов работают попеременно в обеих упомянутых системах координат.
Объем вычислений для любого алгоритма, работающего в объектном пространстве, и сравнивающего каждый объект сцены со всеми остальными объектами этой сцены, растет теоретически как квадрат числа объектов ( n2 ). Аналогично, объем вычислений любого алгоритма, работающего в пространстве изображения и сравнивающего каждый объект сцены с позициями всех пикселов в системе координат экрана, растет теоретически, как nN. Здесь n обозначает количество объектов (тел, плоскостей или ребер) в сцене, а N - число пикселов. Теоретически трудоемкость алгоритмов, работаюoих в объектном пространстве, меньше трудоемкости алгоритмов, работающих в пространстве изображения, при n < N. Поскольку N обычно равно ( 512 )2, то теоретически большинство алгоритмов следует реализовывать в объектном пространстве. Однако на практике это не так. Дело в том, что алгоритмы, работающие в пространстве изображения, более эффективны потому, что для них легче воспользоваться преимуществом когерентности при растровой реализации.
Далее дается изложение некоторых алгоритмов, работающих как в объектном пространстве, так и в пространстве изображения. Каждый из них иллюстрирует одну или несколько основополагающих идей теории алгоритмов удаления невидимых линий и поверхностей.
Алгоритм плавающего горизонта
Алгоритм плавающего горизонта чаще всего используется для удаления невидимых линий трехмерного представления функций, описывающих поверхность в виде
F ( x, у, z ) = 0
Подобные функции возникают во многих приложениях в математике, технике, естественных науках и других дисциплинах.
Существует много алгоритмов, использующих этот подход. Поскольку в приложениях в основном нас интересует описание поверхности, этот алгоритм обычно работает в пространстве изображения. Главная идея данного метода заключается в сведении трехмерной задачи к двумерной путем пересечения исходной поверхности последовательностью параллельных секущих плоскостей, имеющих постоянные значения координат x, y или z.
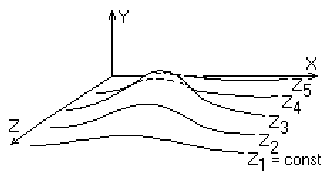
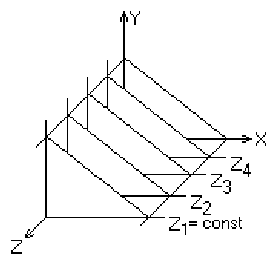
Секущие плоскости с постоянной координатой
На рис. 3.2 приведен пример, где указанные параллельные плоскости определяются постоянными значениями z. Функция F ( x, у, z ) = 0 сводится к последовательности кривых, лежащих в каждой из этих параллельных плоскостей, например к последовательности
y = f ( x, z ) или y = g ( y, z )
где z постоянно на каждой из заданных параллельных плоскостей.
Итак, поверхность теперь складывается из последовательности кривых, лежащих в каждой из этих плоскостей, как показано на рис. 3.3. Здесь предполагается, что полученные кривые являются однозначными функциями независимых переменных. Если спроецировать полученные кривые на плоскость z = 0, то сразу становится ясна идея алгоритма удаления невидимых участков исходной поверхности. Алгоритм сначала упорядочивает плоскости z = const по возрастанию расстояния до них от точки наблюдения. Затем для каждой плоскости, начиная с ближайшей к точке наблюдения, строится кривая, лежащая на ней. Алгоритм удаления невидимой линии заключается в следующем:
Если на текущей плоскости при некотором заданном значении x соответствующее значение y на кривой больше значения y для всех предыдущих кривых при этом значении x, то текущая кривая видима в этой точке; в противном случае она невидима.
Реализация данного алгоритма достаточно проста.
3.4 Обработка нижней стороны поверхности
Для хранения максимальных значений y при каждом значении x используется массив, длина которого равна числу различимых точек (разрешению) по оси x в пространстве изображения. Значения, хранящиеся в этом массиве, представляют собой текущие значения “горизонта”. Поэтому по мере рисования каждой очередной кривой этот горизонт “всплывает”. Фактически этот алгоритм удаления невидимых линий работает каждый раз с одной линией.
Алгоритм работает очень хорошо до тех пор, пока какая-нибудь очередная кривая не окажется ниже самой первой из кривых. Как показано на рис.3.4,а. Подобные кривые, естественно, видимы и представляют собой нижнюю сторону исходной поверхности. Однако алгоритм будет считать их невидимыми. Нижняя сторона поверхности делается видимой, если модифицировать этот алгоритм, включив в него нижний горизонт, который опускается вниз по ходу работы алгоритма. Это реализуется при помощи второго массива, длина которого равна числу различимых точек по оси x в пространстве изображения. Этот массив содержит наименьшие значения y для каждого значения x. Алгоритм теперь становится таким:
Если на текущей плоскости при некотором заданном значении x соответствующее значение y на кривой больше максимума или меньше минимума по y для всех предыдущих кривых при этом x, то текущая кривая видима. В противном случае она невидима.
Полученный результат показан на рис. 3.4, b.
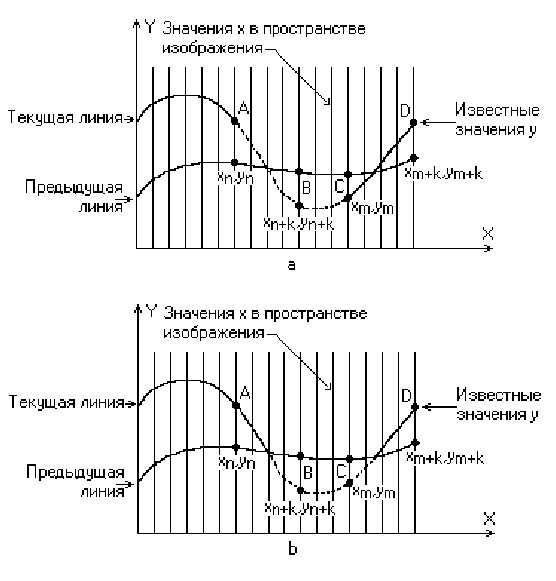
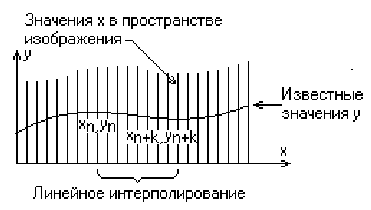
В изложенном алгоритме предполагается, что значение функции, т. е. y, известно для каждого значения x в пространстве изображения. Однако если для каждого значения x нельзя указать (вычислить) соответствующее ему значение у, то невозможно поддерживать массивы верхнего и нижнего плавающих горизонтов. В таком случае используется линейная интерполяция значений у между известными значениями для того, чтобы заполнить массивы верхнего и нижнего плавающих горизонтов, как показано на рис. 3.5.
3.5 Линейная интерполяция между заданными точками
3.6. Эффект пересекающихся кривых
Если видимость кривой меняется, то метод с такой простой интерполяцией не даст корректного результата. Этот эффект проиллюстрирован рис. 3.6,а. Предполагая, что операция по заполнению массивов проводится после проверки видимости, получаем, что при переходе текущей кривой от видимого к невидимому состоянию (сегмент АВ на рис. 3.6,а), точка (xn+k, yn+k ) объявляется невидимой. Тогда участок кривой между точками (xn, yn) и (xn+k, yn+k ) не изображается и операция по заполнению массивов не производится. Образуется зазор между текущей и предыдущей кривыми Если на участке текущей кривой происходит переход от невидимого состояния к видимому (сегмент CD на рис. 3.6,а), то точка (xm+k, ym+k ) объявляется видимой, а участок кривой между точками (xm, ym) и (xm+k, ym+k ) изображается и операция по заполнению массивов проводится. Поэтому изображается и невидимый кусок сегмента CD. Кроме того, массивы плавающих горизонтов не будут содержать точных значений у. А это может повлечь за собой дополнительные нежелательные эффекты для последующих кривы. Следовательно,
необходимо решать задачу о поиске точек пересечения сегментов текущей и предшествующей кривых.
Существует несколько методов получения точек пересечения кривых. На растровых дисплеях значение координаты x можно увеличивать на 1, начиная с xn или xm (рис. 3.6,а). Значение у, соответствующее текущему значению координаты х в пространстве изображения, получается путем добавления к значению у, соответствующему предыдущему значению координаты x, вертикального приращения y вдоль заданной кривой. Затем определяется видимость новой точки с координатами (x + 1, y + y ). Если эта точка видима, то активируется связанный с ней пиксел. Если невидима, то пиксел не активируется, а x увеличивается на 1. Этот процесс продолжается до тех пор, пока не встретится xn+k или xm+k. Пересечения для растровых дисплеев определяются изложенным методом с достаточной точностью. Близкий и даже более элегантный метод определения пересечений основан на двоичном поиске.
Точное значение точки пересечения двух прямолинейных отрезков, которые интерполируют текущую и предшествующую кривые, между точками (xn, yn) и (xn+k, yn+k ) (рис. 3.6) задается формулами:
где
а индексы c и p соответствуют текущей и предшествующей кривым. Полученный результат показан на рис. 3.6,b. Теперь алгоритм излагается более формально.
Если на текущей плоскости при некотором заданном значении x соответствующее значение y на кривой больше максимума или меньше минимума по y для всех предыдущих кривых при этом x, то текущая кривая видима. В противном случае она невидима.
Если на участке от предыдущего (xn) до текущего (xn+k) значения x видимость кривой изменяется, то вычисляется точка пересечения (xi).
Если на участке от xn до xn+k сегмент кривой полностью видим, то он изображается целиком; если он стал невидимым, то изображается фрагмент от xn до xi; если же он стал видимым, то изображается фрагмент от xi до xn+k.
Заполнить массивы верхнего и нижнего плавающих горизонтов.
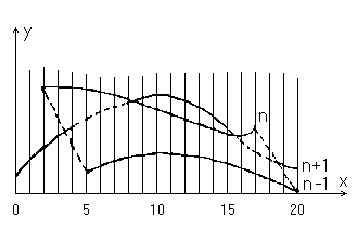
Изложенный алгоритм приводит к некоторым дефектам, когда кривая, лежащая в одной из более удаленных от точки наблюдения плоскостей, появляется слева или справа из-под множества кривых, лежащих в плоскостях, которые ближе к указанной точке наблюдения. Этот эффект продемонстрирован на рис. 3.7, где уже обработанные плоскости n - 1 и n расположены ближе к точке наблюдения. На рисунке показано, что получается при обработке плоскости n + 1. После обработки кривых n - 1 и n верхний горизонт для значений x = 0 и 1 равен начальному значению у; для значений x от 2 до 17 он равен ординатам кривой n; а для значений 18, 19, 20 - ординатам кривой n - 1. Нижний горизонт для значений x = 0 и 1 равен начальному значению у; для значений x = 2, 3, 4 – ординатам кривой n; а для значений x от 5 до 20 - ординатам кривой n - 1. При обработке текущей кривой (n + 1) алгоритм объявляет ее видимой при x = 4. Это показано сплошной линией на рис. 3.7.
3.7 Эффект зазубренного ребра
Аналогичный эффект возникает и справа при x = 18. Такой эффект приводит к появлению зазубренных боковых ребер. Проблема с зазубренностью боковых ребер решается включением в массивы верхнего и нижнего горизонтов ординат, соответствующих штриховым линиям на рис. 3.7. Это можно выполнить эффективно, создав ложные боковые ребра. Приведем алгоритм, реализующий эту идею для обеих ребер.
Обработка левого бокового ребра:
Если Pn является первой точкой на первой кривой, то запомним Pn в качестве Pn1 и закончим заполнение. В противном случае создадим ребро, соединяющее Pn и Pn1.
Занесем в массивы верхнего и нижнего горизонтов ординаты этого ребра и запомним Pn в качестве Pn1.
Обработка правого бокового ребра:
Если Pn является последней точкой на первой кривой, то запомним Pn в качестве Pn1 и закончим заполнение. В противном случае создадим ребро, соединяющее Pn и Pn1.
Занесем в массивы верхнего и нижнего горизонтов ординаты этого ребра и запомним Pn в качестве Pn1.
Теперь полный алгоритм выглядит так:
Для каждой плоскости z = const.
Обработать левое боковое ребро.
Для каждой точки, лежащей на кривой из текущей плоскости:
Если при некотором заданном значении x соответствующее значение у на кривой больше максимума или меньше минимума по у для всех предыдущих кривых при этом x, то кривая видима (в этой точке). В противном случае она невидима.
Если на сегменте от предыдущего (xn) до текущего (xn+k) значения x видимость кривой изменяется, то вычисляется пересечение (xi).
Если на участке от xn до (xn+k) сегмент кривой полностью видим, то он изображается целиком; если он cтал невидимым, то изображается его кусок от xn до xi; если же он стал видимым, то изображается его кусок от xi до xn+k.
Заполнить массивы верхнего и нижнего плавающих горизонтов.
Обработать правое боковое ребро.
Если функция содержит очень острые участки (пики), то приведенный алгоритм может дать некорректные результаты. Во избежании этого если встречаются узкие участки, то функцию следует вычислять в большем числе точек.
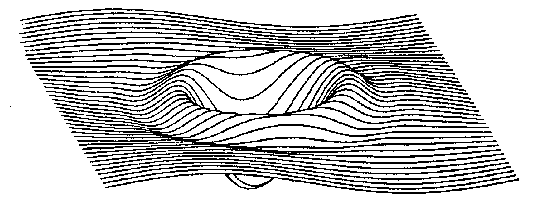
3.8 Функция y = (1/5) sin x cos z (3/2) cos (7a/4) * exp (a), a = (x )2 + (z )2, изображённая в интервале (0, 2) с помощью алгоритма плавающего горизонта
На рис. 3.8 показан типичный результат работы алгоритма плавающего горизонта. Запись этого алгоритма приводиться ниже.
Алгоритм плавающего горизонта
Гэкран – разрешение экрана в горизонтальном направлении
Вэкран – разрешение экрана в вертикальном направлении
Верх – массив, содержащий координаты верхнего горизонта
Низ – массив, содержащий координаты нижнего горизонта
Y – текущее значение функции y = f ( x, z ) при z = const
Тфлаг – флаг видимости для текущей точки
Пфлаг – флаг видимости для предыдущей точки, равный
0 = невидима
1 = видима и выше верхнего горизонта
-1 = видима и ниже нижнего горизонта
Draw – графическая команда, которая чертит видимую линию между точками, заданными их координатами.
Xmin, Xmax – минимальная и максимальная абсциссы функции
Xшаг – шаг приращения вдоль оси x
Zmin, Zmax – минимальная и максимальная аппликата функции
Zшаг – шаг между плоскостями z = const
Dimension Верх (Гэкран), Низ (Гэкран)
инициализация переменных
Xлевое = 1; Yлевое = 1; Xправое = 1; Yправое = 1
инициализация массивов горизонтов
Верх = 0
Низ = Вэкран
Вычисление функции на каждой плоскости z = const, начиная с ближайшей к наблюдателю плоскости Zmax
for z = Zmax to Zmin step Zшаг
инициализация предыдущих значений по x и y: Xпред и Yпред
Xпред = Xmin
Yпред = f (Xmin, z)
если используется видовое преобразование, то его нужно применить к Xпред, Yпред, z в данной точке
обработка левого бокового ребра
call Обрребра (Xпред, Yпред, Xлев, Yлев; Верх, Низ)
call Видимость (Xпред, Yпред, Верх, Низ; Пфлаг)
для каждой точки на кривой, лежащей в плоскости z = const
for x = Xmin to Xmax step Xшаг
y = f (x, z)
если используется видовое преобразование, то его нужно применить к данной точке
проверка видимости текущей точки и заполнение соответствующего массива горизонта
call Видимость (x, y, Верх, Низ; Тфлаг)
if Тфлаг = Пфлаг then
if (Тфлаг = 1) or (Тфлаг = 1) then
Draw (Xпред, Yпред, x, y)
call Горизонт (Xпред, Yпред, x, y; Верх, Низ)
end if
если видимость изменилась, то вычисляется пересечение и заполняется массив горизонта
else
if Тфлаг = 0 then
if Пфлаг = 1 then
call Пересечение (Xпред, Yпред, x, y, Верх; Xi, Yi)
else
call Пересечение (Xпред, Yпред, x, y, Низ; Xi, Yi)
end if
Draw (Xпред, Yпред, Xi, Yi)
сall Горизонт (Xпред, Yпред, Xi, Yi, Верх, Низ)
else
if Тфлаг = 1 then
if Пфлаг = 0 then
call Пересечение (Xпред, Yпред, x, y, Верх; Xi, Yi)
Draw (Xi, Yi, x, y)
сall Горизонт (Xi, Yi, x, y; Верх, Низ)
else
call Пересечение (Xпред, Yпред, x, y, Низ; Xi, Yi)
Draw (Xпред, Yпред, Xi, Yi)
call Горизонт (Xпред, Yпред, Xi, Yi; Верх, Низ)
call Пересечение (Xпред, Yпред, x, y, Верх; Xi, Yi)
Draw (Xi, Yi, x, y)
call Горизонт (Xi, Yi, x, y; Верх, Низ)
end if
else
if Пфлаг = 0 then
call Пересечение (Xпред, Yпред, x, y, Верх; Xi, Yi)
Draw (Xi, Yi, x, y)
call Горизонт (Xi, Yi, x, y; Верх, Низ)
else
call Пересечение (Xпред, Yпред, x, y, Верх; Xi, Yi)
Draw (Xпред, Yпред, Xi, Yi)
call Горизонт (Xпред, Yпред, Xi, Yi; Верх, Низ)
call Пересечение (Xпред, Yпред, x, y, Низ; Xi, Yi)
Draw (Xi, Yi, x, y)
call Горизонт (Xi, Yi, x, y; Верх, Низ)
end if
end if
end if
end if
вновь инициализировать Пфлаг, Xпред, Yпред
Пфлаг = Тфлаг
Xпред = x
Yпред = y
next x
обработка правого концевого ребра
call Обрребра (x, y, Xправ, Yправ; Верх, Низ)
next z
finish
подпрограмма обработки бокового ребра
Subroutine Обрребра (x, y, Xребра, Yребра; Верх, Низ)
если Xребра = 1, то встречена первая кривая и ребро не создаётся
if Xребра = 1 then 1
call Горизонт (Xребра, Yребра, x, y; Верх, Низ)
1 Xребра = x
Yребра = y
return
подпрограмма определения видимости точки
Subroutine Видимость (x, y, Верх, Низ; Тфлаг)
видимость точки определяется по отношению к верхнему и нижнему плавающим горизонтам. Если точка лежит на самом горизонте, то она считается видимой.
Тфлаг = 0, если точка невидима
= 1, если она видима и выше верхнего горизонта
= 1, если она видима и ниже нижнего горизонта
x считается целой
if (y < Верх (x)) and (y > Низ (x)) then Тфлаг = 0
if y Верх (x) then Тфлаг = 1
if y Низ (x) then Тфлаг = 1
return
подпрограмма заполнения массивов плавающих горизонтов
Subroutine Горизонт (X1, Y1, X2, Y2; Верх, Низ)
Эта программа использует линейную интерполяцию для заполнения массивов горизонтов между X1 и X2
Max (a, b) – определяет большее из a и b
Min (a, b) – определяет меньшее из a и b
проверка вертикальности наклона
if (X2 X1) = 0 then
Верх (X2) = Max (Верх (X2), Y2)
Низ (X2) = Min (Низ (X2), Y2)
else
Наклон = (Y2 Y1)/(X2 X1)
for x = X1 to X2 step 1
y = Наклон * (x X1) + Y1
Верх (x) = Max (Верх (x), y)
Низ (x) = Min (Низ (x), y)
next x
end if
return
подпрограмма вычисления пересечения текущей кривой с горизонтом
Subroutine Пересечение (X1, Y1, X2, Y2, Массив; Xi, Yi)
Эта процедура вычисляет пересечение двух отрезков прямых
Массив содержит информацию о соответствующем горизонте
Sign – функция принимающая значения 1, 0, 1, если знак её аргумента <0, =0, >0 соответственно
проверка бесконечности наклона
if (X2 – X1) = 0 then
Xi = X2
Yi = Массив (X2)
else
вычисление пересечения
обход начинается с самой левой используемой точки
пересечение считается обнаруженным, когда изменяется знак разности значений y
Наклон = (Y2 – Y1)/(X2 – X1)
Ysign = Sign (Y1 + Наклон Массив (X1 + 1))
Csign = Ysign
Yi = Y1 + Наклон
Xi = X1 + 1
while Csign = Ysign
Yi = Y1 + Наклон
Xi = X1 + 1
Csign = Sign (Yi - Массив (Xi))
end while
выбирается ближайшее целое число
if |Yi Наклон Массив (X1 – 1)| |Yi Наклон Массив (X1)| then
Yi = Y1 – Наклон
Xi = X1 – 1
end if
end if
return
В приведенных выше алгоритме и примере функция у = f (x, z) рассматривалась только при z = const. Часто бывает удобно вычерчивать кривые, полагая постоянными как z, так и x. При этом возникает эффект перекрестной штриховки. На первый взгляд может показаться, что перекрестную штриховку можно получить путем наложения двух результатов, образованных плоскостями z = const и x = const. Однако это не так. Верный результат получается при обработке тех кривых из числа лежащих в плоскостях z = const и x = const, которые ближе всего к горизонтальным при обычном порядке их следования. Однако после обработки каждой кривой, самой близкой к горизонтальной, необходимо обрабатывать участки кривых, лежащих в ортогональных ей плоскостях, которые находятся между указанной кривой и кривой, следующей за ней. Разумеется, при обработке обеих последовательностей кривых нужно использовать одни и те же массивы верхнего и нижнего плавающих горизонтов. Если используется перекрестная штриховка, то не надо формировать левое и правое боковые ребра.
Алгоритм Робертса
Алгоритм Робертса представляет собой первое известное решение задачи об удалении невидимых линий . Это математически элегантный метод, работающий в объектном пространстве. Алгоритм, прежде всего, удаляет из каждого тела те ребра или грани, которые экранируются самим телом. Затем каждое из видимых ребер каждого тела сравнивается с каждым из оставшихся тел для определения того, какая его часть или части, если таковые есть, экранируются этими телами. Поэтому вычислительная трудоемкость алгоритма Робертса растет теоретически как квадрат числа объектов. Именно этот факт привёл к снижению интереса к алгоритму Робертса. Однако математические методы, используемые в этом алгоритме, просты, мощны и точны. Кроме того, этот алгоритм можно использовать для иллюстрации некоторых важных концепций. Наконец, более поздние реализации алгоритма, использующие предварительную приоритетную сортировку вдоль оси z и простые габаритные или минимаксные тесты, демонстрируют почти линейную зависимость от числа объектов.
В алгоритме Робертса требуется, чтобы все изображаемые тела или объекты были выпуклыми. Невыпуклые тела должны быть разбиты на выпуклые части. В этом алгоритме выпуклое многогранное тело с плоскими гранями должно представляться набором пересекающихся плоскостей. Уравнение произвольной плоскости в трехмерном пространстве имеет вид
ах + by + cz + d = 0 (3.1)
В матричной форме это выглядит так:
или
где представляет собой плоскость. Поэтому любое выпуклое твердое тело можно выразить матрицей тела, состоящей из коэффициентов уравнений плоскостей, т. е.
где каждый столбец содержит коэффициенты одной плоскости.
Напомним, что любая точка пространства представима в однородных координатах вектором
Более того, если точка [S] лежит на плоскости, то [S]*[P]T = 0. Если же [S] не лежит на плоскости, то знак этого скалярного произведения показывает, по какую сторону от плоскости расположена точка. В алгоритме Робертса предполагается, что точки, лежащие внутри тела, дают положительное скалярное произведение.
Хотя уравнение плоскости (3.1) содержит четыре неизвестных коэффициента, его можно нормировать так, чтобы d = 1 следовательно, трех неколлинеарных точек достаточно для определения этих коэффициентов. Подстановка координат трех неколлинеарных точек (x1, y1, z1), (x2, y2, z2), (x2, y2, z2) в нормированное уравнение (3.1) дает:
ax1 + by1 + cz1 = 1
ax2 + by2 + cz2 = 1
ax3 + by3 + cz3 = 1
В матричной форме это выглядит так:
или
(3.2)
Решение этого уравнения дает значения коэффициентов уравнения плоскости:
Другой способ используется, если известен вектор нормали к плоскости, т. е.
n = ai + bj + ck
где i, j, k - единичные векторы осей x, y, z соответственно. Тогда уравнение плоскости примет вид
ax + by + cz + d = 0(3.3)
Величина d вычисляется с помощью произвольной точки на плоскости. В частности, если компоненты этой точки на плоскости (х1, y1, z1) то:
d = (aх1 + by1 + cz1) (3.4)
Поскольку объем вычислений в алгоритмах удаления невидимых линий или поверхностей растет с увеличением числа многоугольников, для описания поверхностей выгодно использовать многоугольники с более чем тремя сторонами. Эти многоугольники могут быть как невыпуклыми, так и неплоскими. Метод, предложенный Мартином Ньюэлом, позволяет найти как точное решение для уравнений плоскостей, содержащих плоские многоугольники, так и “наилучшее” приближение для неплоских многоугольников. Этот метод эквивалентен определению нормали в каждой вершине многоугольника посредством векторного произведения прилежащих ребер и усреднения результатов. Если a, b, c, d – коэффициенты уравнения плоскости, то
(3.5)
где
if i =n then j = 1 else j = i + 1
а d вычисляется с помощью любой точки на плоскости.
Перед началом работы алгоритма удаления невидимых линий или поверхностей для получения желаемого вида сцены часто применяется трехмерное видовое преобразование. Матрицы тел для объектов преобразованной сцены можно получить или преобразованием исходных матриц тел или вычислением новых матриц тел, используя преобразованные вершины или точки.
Если [В] - матрица однородных координат, представляющая исходные вершины тела, а [Т] - матрица размером 4х4 видового преобразования, то преобразованные вершины таковы:
[ВТ] = [В][T] (3.6)
где [ВТ] - преобразованная матрица вершин. Использование уравнения (3.2) позволяет получить уравнения исходных плоскостей, ограничивающих тело:
[В][V] = [D] (3.7)
где [V] - матрица тела, а [D] в правой части - нулевая матрица. Аналогично уравнения преобразованных плоскостей задаются следующим образом:
[ВТ][VТ] = [D] (3.8)
где [VТ] - преобразованная матрица тела. Приравнивая левые части уравнения (3.7) и (3.8), получаем
[ВТ][VT] = [В][V]
Подставляя уравнение (3.6), сокращая на [В] и умножая слева на
[T]-1 имеем
[VT] = [T]-1[V]
Итак, преобразованная матрица тела получается умножением исходной матрицы тела слева на обратную матрицу видового преобразования.
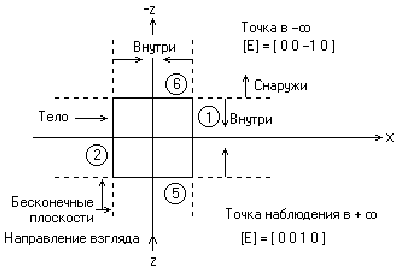
3.8 Не лицевые плоскости
Тот факт, что плоскости имеют бесконечную протяженность и что скалярное произведение точки на матрицу тела отрицательно, если точка лежит вне этого тела, позволяет предложить метод, в котором матрица тела используется для определения граней, которые экранируются самим этим телом. Отрицательное скалярное произведение даёт только такая плоскость (столбец) в матрице тела, относительно которой точка лежит снаружи.
Если зритель находится в бесконечности на положительной полуоси z и смотрит на начало координат, то его взгляд направлен в сторону отрицательной полуоси z. В однородных координатах вектор такого направления равен:
который служит, кроме того, образом точки, лежащей в бесконечности на отрицательной полуоси z. Фактически [Е] представляет любую точку, лежащую на плоскости z = , т. е. любую точку типа (x, y, ). Поэтому, если скалярное произведение [Е] на столбец, соответствующий какой-нибудь плоскости в матрице тела, отрицательно, то [Е] лежит по отрицательную сторону этой плоскости. Следовательно, эти плоскости невидимы из любой точки наблюдения, лежащей в плоскости z = , а пробная точка на z = экранируется самим телом, как показано на рис. 3.8. Такие плоскости называются не лицевыми, а соответствующие им грани задними. Следовательно,
[Е][V] < 0
является условием того, что плоскости – не лицевые, а их грани - задние. Заметим, что для аксонометрических проекций (точка наблюдения в бесконечности) это эквивалентно поиску положительных значений в третьей строке матрицы тела.
Этот метод является простейшим алгоритмом удаления невидимых поверхностей для тел, представляющих собой одиночные выпуклые многогранники. Этот способ часто называют отбрасыванием задних плоскостей. Для выпуклых многогранников число граней при этом сокращается примерно наполовину. Метод эквивалентен вычислению нормали к поверхности для каждого отдельного многоугольника. Отрицательность нормали к поверхности показывает, что нормаль направлена в сторону от наблюдателя и, Следовательно, данный многоугольник не виден.
Этот метод можно использовать также и для простой закраски. Интенсивность или цветовой оттенок многоугольника делается пропорциональным проекции нормали к поверхности на направление взгляда.
Данный метод определения не лицевых граней в результате формирует аксонометрическую проекцию на некую плоскость, расположенную бесконечно далеко от любой точки трехмерного пространства. Видовые преобразования, включая перспективное, производятся до определения не лицевых плоскостей. Когда видовое преобразование включает в себя перспективу, то нужно использовать полное перспективное преобразование одного трехмерного пространства в другое, а не перспективное проецирование на некоторую двумерную плоскость. Полное перспективное преобразование приводит к искажению трехмерного тела, которое затем проецируется на некую плоскость в бесконечности, когда не лицевые плоскости уже определены. Этот результат эквивалентен перспективному проецированию из некоторого центра на конечную плоскость проекции.
Видовое преобразование можно применить к телу так, чтобы точка наблюдения оставалась фиксированной. При другом способе тело остается неподвижным. Соответствующие точка наблюдения и направление взгляда получаются умножением справа на матрицу, обратную матрице видового преобразования.
После определения нелицевых плоскостей остается найти нелицевые отрезки. Нелицевой отрезок образуется в результате пересечения пары нелицевых плоскостей. После первого этапа удаления нелицевых отрезков необходимо выяснить, существуют ли такие отрезки, которые экранируются другими телами на картинке или в сцене. Для этого каждый оставшийся отрезок или ребро нужно сравнить с другими телами сцены или картинки. При этом использование приоритетной сортировки (z–сортировки) и простого минимаксного или габаритного с прямоугольной объемлющей оболочкой тестов позволяет удалить целые группы или кластеры отрезков и тел. Например, если все тела в сцене упорядочены в некотором приоритетном списке, использующем значения z ближайших вершин для представления расстояния до наблюдателя, то никакое тело из этого списка, у которого ближайшая вершина находится дальше от наблюдателя, чем самая удаленная из концевых точек ребра, не может закрывать это ребро. Более того, ни одно из оставшихся тел, прямоугольная оболочка которого расположена полностью справа, слева, над или под ребром, не может экранировать это ребро. Использование этих приемов значительно сокращает число тел, с которыми нужно сравнивать каждый отрезок или ребро.
Для сравнения отрезка P1P2 с телом удобно использовать параметрическое представление этого отрезка:
Р(t) = P1 + (Р2 - P1)t 0 t 1
v = s + dt
где v - вектор точки на отрезке, s - начальная точка, d - направление отрезка. Необходимо определить, будет ли отрезок невидимым. Если он невидим, то надо найти те значения t, для которых он невидим. Для этого формируется другой параметрический отрезок от точки Р(t) до точки наблюдения g:
Q(a,t) = u = v + ga = s + dt + ga 0 t 1, a 0
Здесь a и t выполняют аналогичные функции. Заданное значение t указывает точку на отрезке P(t), а a указывает точку на отрезке, проведенном от точки P(t) до точки наблюдения. Фактически Q(a,t) представляет собой плоскость в трехмерном пространстве. Пара (a,t) определяет точку на этой плоскости. Значение a положительно, поскольку тела, экранирующие P(t) могут находиться только в той части этой плоскости, которая заключена между отрезком P(t) и точкой наблюдения.
Скалярное произведение любой точки, лежащей внутри тела, на матрицу тела положительно. Если же точка лежит внутри тела, то она невидима. Поэтому для определения части отрезка, которая экранируется телом, достаточно найти те значения a и t, для которых скалярное произведение Q(a,t) = u на матрицу тела положительно.
3.9 Схема решения относительно a и t
Это скалярное произведение равно:
h = u * [VT] = s * [VT] + td * [VT] + ag * [VT] >0 0 t 1, a 0
Если все компоненты h неотрицательны для некоторых t и a, отрезок при этих значениях t экранируется данным телом. Обозначим
p = s * [VT]
q = d * [VT]
w = g * [VT]
запишем условия в виде
hj = pj + tqj + awj 0 t 1, a 0
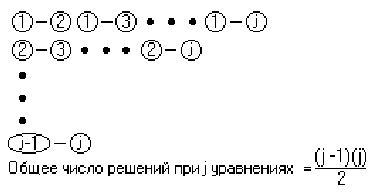
где j - номер столбца в матрице тела. Эти условия должны выполняться при всех значениях j, т. е. для всех плоскостей, ограничивающих объем тела. Пограничный случай между видимостью и невидимостью возникает, когда hj = 0. При hj = 0 точка лежит на плоскости. Полагая hj = 0 для всех плоскостей, мы получим систему уравнений относительно a и t, которые должны удовлетворяться одновременно. Результат можно получить путем совместного решения всевозможных пар уравнений из этой системы, при этом будут найдены все значения a и t, при которых изменяется значение видимости отрезка. Схема решения показана на рис. 3.10. Число возможных решений при j уравнениях (плоскостях) равно j(j 1)/2. Каждое решение в диапазонах 0 t 1, a 0, подставляется во все остальные уравнения для проверки того, что условие hj 0 выполнено. Поиск корректных решений производится для того, чтобы найти минимальное среди максимальных значений параметра t(tminmax) и максимальное среди минимальных значений t(tmaxmin). Отрезок невидим при (tmaxmin) < t < (tminmax). Последнее требование является простым следствием из классической задачи линейного программирования.
Решение на границе a = 0 возникает в случае протыкания (объектов).
Один из приемов заключается в запоминании всех точек протыкания и в добавлении к сцене отрезков, связывающих эти точки. Отрезки образуются путем соединения каждой точки протыкания пары тел, связанных отношением протыкания, со всеми остальными точками протыкания для этой пары объектов. Затем проверяется экранирование этих отрезков данными телами. Видимые отрезки образуют структуру протыкания.
Из практики известно, что решения удовлетворяющие неравенствам hj > 0, могут существовать и за пределами области, ограниченной условиями 0 t 1 и a = 0. Поэтому три уравнения, описывающие эти границы, т.е. t = 0, t 1 = 0 и a = 0, нужно добавить к множеству уравнений hj = 0. Теперьчисло решений равно (j + 2)(j + 3)/2, где j - количество плоскостей, ограничивающих выпуклый объем тела.
Как упоминалось ранее, выбор максимального из минимального и минимального из максимальных значений t среди возможных корректных решений указанной системы уравнений является простой задачей линейного программирования. Ее решение эквивалентно определению корректной ограниченной области, получающейся в результате графического решения. Предполагается, что этот алгоритм используется только для таких отрезков, о которых известно, что они частично или полностью невидимы. Все нелицевые и все полностью видимые отрезки выявлены и удалены до начала работы алгоритма. Алгоритм начинает работу с такими значениями t и a, которые являются решениями пары линейных уравнений с номерами е1 и е2, а также с tmin и tmax (текущими минимальным и максимальным значениями t) и с n (мощностью множества уравнений). На первом этапе алгоритма проверяется выполнение условий hj > 0. Если эти условия выполнены, то на втором этапе вычисляются значения tmin и tmax. Результатом являются значения tmaxmin и tminmax.
Метод решения, обсуждавшийся выше, требует больших затрат машинного времени. Поэтому стоит поискать более быстрые способы определения полностью видимых отрезков. Основная: идея состоит в установлении того факта, что оба конца отрезка лежат между точкой наблюдения и какой-нибудь видимой плоскостью. Т.к.
u = s + td + ag
При a = 0 значение u задает сам отрезок. Далее, если a = 0, при t = 0 и t = 1 получаются концевые точки отрезка. Также известно, что
hj = u *[VT] = pj + qjt+ wja
и заметим, что при t = 0 pj является скалярным произведением концевой точки отрезка и j-й плоскости, ограничивающей тело. Аналогично pj + qj является скалярным произведением другой концевой точки отрезка и j-й плоскости, ограничивающей тело. Наконец, напомним, что j-я плоскость, ограничивающая тело, видима, если wj = 0. Поэтому, если wj О и pj 0, то один конец отрезка лежит или на видимой плоскости или между видимой плоскостью и точкой наблюдения. Если же pj + qj 0, то другой конец отрезка также лежит либо на видимой плоскости, либо между этой плоскостью и точкой наблюдения. Следовательно, отрезок полностью видим, если для любого j
wj О и pj 0 и pj + qj 0.
Эти условия гарантируют, что неравенства hj 0 не могут быть выполнены ни при каких a 0 и 0 t 1. Поэтому никакая часть отрезка не может быть невидимой, т. е. отрезок полностью видим.
Ниже приводится эффективная реализация алгоритма Робертса. Этот алгоритм делится на три этапа. На первом этапе каждое тело анализируется индивидуально с целью удаления нелицевых плоскостей. На втором этапе проверяется экранирование оставшихся в каждом теле ребер всеми другими телами с целью обнаружения их невидимых отрезков. На третьем этапе вычисляются отрезки, которые образуют новые ребра при протыкании телами друг друга. В данном алгоритме предполагается, что тела состоят из плоских полигональных граней, которые в свою очередь состоят из рёбер, а ребра - из отдельных вершин. Все вершины, ребра и грани связаны с конкретным телом.
Удаление нелицевых плоскостей
Для каждого тела в сцене:
Сформировать многоугольники граней и ребра, исходя из списка вершин тела.
Вычислить уравнение плоскости для каждой полигональной грани тела.
Проверить знак уравнения плоскости:
Взять любую точку внутри тела, например усреднив координаты его вершин.
Вычислить скалярное произведение уравнения плоскости и точки внутри тела.
Если это скалярное произведение < О, то изменить знак уравнения этой плоскости.
Сформировать матрицу тела.
Умножить ее слева на матрицу, обратную матрице видового преобразования, включающего перспективу.
Вычислить и запомнить габариты прямоугольной объемлющей оболочки преобразованного объема: xmin, xmax, ymin, ymax.
Определить нелицевые плоскости:
Вычислить скалярное произведение пробной точки, лежащей в бесконечности, на преобразованную матрицу тела.
Если это скалярное произведение < О, то плоскость невидима.
Удалить весь многоугольник, лежащий в этой плоскости. Это избавляет от необходимости отдельно рассматривать, невидимые линии, образуемые пересечением пар невидимых плоскостей.
Удаление из каждого тела тех ребер, которые экранируются всеми остальными телами в сцене:
Если задано только одно тело, то алгоритм завершается.
Сформировать приоритетный список этих тел:
Провести сортировку по z. Сортировка производится по максимальным значениям координаты z вершин преобразованных тел. Первым в упорядоченном списке и обладающим наибольшим приоритетом будет то тело, у которого минимальное среди максимальных значений z. В используемой правой системе координат это тело будет самым удаленным от точки наблюдения, расположенной в бесконечности на оси z.
Для каждого тела из приоритетного списка:
Проверить экранирование всех лицевых ребер всеми другими телами сцены. Тело, ребра которого проверяются, называется пробным объектом, а тело, относительно которого в настоящий момент производится проверка, называется пробным телом. Естественно, что нужно проверять экранирование пробного объекта только теми пробными телами, у которых ниже приоритеты.
Провести проверки экранирования для прямоугольных объемлющих оболочек пробного объекта и пробного тела:
Еслиxmin (пробное тело) > xmax (пробный объект) или
xmax (пробное тело) < xmin (пробный объект) или
ymin (пробное тело) > ymax (пробный объект) или
ymax (пробное тело) < ymin (пробный объект),
то пробное тело не может экранировать ни одного ребра пробного объекта. Перейти к следующему пробному телу. В противном случае:
Провести предварительные проверки протыкания, чтобы увидеть, не протыкается ли пробное тело пробным объектом и существует ли возможность частичного экранирования первого последним.
Сравнить максимальное значение z у пробного объекта с минимальным значением z у пробного тела.
Если zmax (пробный объект) < zmin (пробное тело), то протыкание невозможно. Перейти к следующему телу. В противном случае:
Проверить видимое протыкание.
Если zmin (пробный объект) > zmax (пробное тело), то пробный объект может проткнуть переднюю грань пробного тела.
Установить флаг видимого протыкания для последующего использования. Занести проткнутое тело в список протыканий.
Если xmax (пробное тело) > xmin (пробный объект) или
xmin (пробное тело) < xmax (пробный объект),
то пробный объект может проткнуть бок пробного тела.
Установить флаг видимого протыкания для последующего использования. Завести тело в список протыканий.
Если ymax (пробное тело) > ymin (пробный объект) или
ymin (пробное тело) < ymax (пробный объект),
то пробный объект может проткнуть верх или виз пробного тела.
Установить флаг видимого протыкания для последующего использования. Занести проткнутое тело в список протыканий.
Если список протыканий пуст, то устанавливать флаг протыкания не надо.
Провести проверки экранирования ребер:
Вычислить s и d для ребра.
Вы числить p, q, w для каждой плоскости, несущей грань пробного тела.
Проверка полной видимости. Если ребро полностью, видимо, то перейти к следующему ребру.
Сформировать уравнения hj = 0 и решить их, объединяя попарно и включив в систему уравнения границ t = 0 и t = 1. Если установлен флаг видимого протыкания, то в систему надо включить и уравнение границы a = 0. Запомнить точки протыкания. В противном случае границу a = 0 не учитывать.
Для каждой пары (t, a), являющейся решением проверить выполнение условий 0 t 1, a 0 и hj > 0 для всех других плоскостей. Если эти условия выполнены, то найти tmaxmin и tminmax.
Вычислить видимые участки отрезков и сохранить их для последующей проверки экранирования телами с более низкими приоритетами.
Определить видимые отрезки, связывающие точки протыкания:
Если флаг видимого протыкания не установлен, перейти к процедуре визуализации.
Если точек протыкания не обнаружено, перейти к процедуре визуализации.
Сформировать все возможные ребра, соединяющие точки протыкания, для пар тел, связанных отношением протыкания.
Проверить экранирование всех соединяющих ребер обоими телами, связанными отношением протыкания.
Проверить экранирование оставшихся соединяющих ребер всеми прочими телами сцены. Запомнить видимые отрезки.
Визуализировать оставшиеся видимые отрезки ребер.
Алгоритм использующий Z-буфер
Это один из простейших алгоритмов удаления невидимых поверхностей. Работает этот алгоритм в пространстве изображения. Идея z-буфера является простым обобщением идеи о буфере кадра. Буфер кадра используется для запоминания атрибутов (интенсивности) каждого пиксела в пространстве изображения. Z-буфер - это отдельный буфер глубины, используемый для запоминания координаты z или глубины каждого видимого пиксела в пространстве изображения. В процессе работы глубина или значение z каждого нового пиксела, который нужно занести в буфер кадра, сравнивается с глубиной того пиксела, который уже занесен в z-буфер. Если это сравнение показывает, что новый пиксел расположен впереди пиксела, находящегося в буфере кадра, то новый пиксел заносится в этот буфер и, кроме того, производится корректировка z-буфера новым значением z. Если же сравнение дает противоположный результат, то никаких действий не производится. По сути, алгоритм является поиском по x и y наибольшего значения функции z (z, y).
Главное преимущество алгоритма - его простота. Кроме того, этот алгоритм решает задачу об удалении невидимых поверхностей и делает тривиальной визуализацию пересечений сложных поверхностей. Сцены могут быть любой сложности. Поскольку габариты пространства изображения фиксированы, оценка вычислительной трудоемкости алгоритма не более чем линейна. Поскольку элементы сцены или картинки можно заносить в буфер кадра или в z-буфер в произвольном порядке, их не нужно предварительно сортировать по приоритету глубины. Поэтому экономится вычислительное время, затрачиваемое на сортировку по глубине.
Основной недостаток алгоритма - большой объем требуемой памяти. Если сцена подвергается видовому преобразованию и отсекается до фиксированного диапазона координат z значений, то можно использовать z-буфер с фиксированной точностью. Информацию о глубине нужно обрабатывать с большей точностью, чем координатную информацию на плоскости (x, y); обычно бывает достаточно 20 бит. Буфер кадра размером 512х512х24 бит в комбинации с z-буфером размером 512х512х20 бит требует почти 1.5 мегабайт памяти. Однако снижение цен на память делает экономически оправданным создание специализированных запоминающих устройств для z-буфера и связанной с ним аппаратуры.
Альтернативой созданию специальной памяти для z-буфера является использование для этой цели оперативной или массовой памяти. Уменьшение требуемой памяти достигается разбиением пространства изображения на 4, 16 или больше квадратов или полос. В предельном варианте можно использовать z-буфер размером в одну строку развертки. Для последнего случая имеется интересный алгоритм построчного сканирования. Поскольку каждый элемент сцены обрабатывается много раз, то сегментирование z-буфера, вообще говоря, приводит к увеличению времени, необходимого для обработки сцены. Однако сортировка на плоскости, позволяющая не обрабатывать все многоугольники в каждом из квадратов или полос, может значительно сократить этот рост.
Другой недостаток алгоритма z-буфера состоит в трудоемкости и высокой стоимости устранения лестничного эффекта, а также реализации эффектов прозрачности и просвечивания.
Более формальное описание алгоритма z-буфера таково:
Заполнить буфер кадра фоновым значением интенсивности или цвета.
Заполнить z-буфер минимальным значением z.
Преобразовать каждый многоугольник в растровую форму в произвольном порядке.
Для каждого Пиксел(x, y) в многоугольнике вычислить его глубину z (x, y).
Сравнить глубину z (x, y) со значением Z буфер(x, y), хранящимися в z-буфере в этой же позиции.
Если z (x, y) > z буфер (x, y), то записать атрибут этого многоугольника (интенсивность, цвет и т. п.) в буфер кадра и заменить z-буфер(x, y) на z (x, y).
В противном случае никаких действий не производить.
В качестве предварительного шага там, где это целесообразно, применяется удаление нелицевых граней.
Если известно уравнение плоскости, несущей каждый многоугольник, то вычисление глубины каждого пиксела на сканирующей строке можно проделать пошаговым способом. Как известно уравнение плоскости имеет вид
ax + by + cz + d =0
z = ( ax + by + d)/c 0
Для сканирующей строки y = const. Поэтому глубина пиксела наэтой строке, у которого x = x + x, равна
z1 z = (ax1 + d)/c + (ax + d)/c = a(x x1)/c
или
z1 = z – (a/c)x
Но x = 1, поэтому z1 = (а/с).
Алгоритм, использующий z-буфер, можно также применить для построения сечений поверхностей. Изменится только оператор сравнения:
z(x, y) > z-буфер(x, y) and z(x, y) Zсечения
где Zсечения - глубина искомого сечения. Эффект заключается в том, что остаются только такие элементы поверхности, которые лежат на самом сечении или позади него.
Алгоритм определения видимых поверхностей путём трассировки лучей
Оценки эффективности всех алгоритмов удаления невидимых поверхностей, изложенных ранее, зависят от определенных характеристик когерентности той сцены, для которой ведется поиск ее видимых участков. В отличие от них трассировка лучей является методом грубой силы. Главная идея, лежащая в основе этого метода, заключается в том, что наблюдатель видит любой объект посредством испускаемого неким источником света, который падает на этот объект и затем каким-то путем доходит до наблюдателя. Свет может достичь наблюдателя, отразившись от поверхности, преломившись или пройдя через нее. Если проследить за лучами света, выпущенными источником, то можно убедиться, что весьма немногие из них дойдут до наблюдателя. Следовательно, этот процесс был бы вычислительно неэффективен. В следствии этого было предложено отслеживать (трассировать) лучи в обратном направлении, т. е. от наблюдателя к объекту, как показано на рис. 3.11. В первом алгоритме трассировка прекращалась, как только луч пересекал поверхность видимого непрозрачного объекта; т. е. луч использовался только для обработки скрытых или видимых поверхностей. С течением времени был реализован алгоритм трассировки лучей с использованием общих моделей освещения. Эти алгоритмы учитывают эффекты отражения одного объекта от поверхности другого, преломления, прозрачности и затенения. Производится также устранение ступенчатости. Рассмотрим применением метода трассировки лучей для определения видимых или скрытых поверхностей.
3.11. Простая трассировка лучей
Рис.3.11 служит иллюстрацией алгоритма трассировки лучей. В этом алгоритме предполагается, что сцена уже преобразована в пространство изображения. Перспективное преобразование не используется. Считается, что точка зрения или наблюдатель находится в бесконечности на положительной полуоси z. Поэтому все световые лучи параллельны оси z. Каждый луч, исходящий от наблюдателя, проходит через центр пиксела на растре до сцены. Траектория каждого луча отслеживается, чтобы определить, какие именно объекты сцены, если таковые существуют, пересекаются с данным лучом. Необходимо проверить пересечение каждого объекта сцены с каждым лучом.
3.12. Трассировка луча с учётом перспективы
Если луч пересекает объект, то определяются всевозможные точки пересечения луча и объекта. Можно получить большое количество пересечений, если рассматривать много объектов. Эти пересечения упорядочиваются по глубине. Пересечение с максимальным значением z представляет видимую поверхность для данного пиксела. Атрибуты этого объекта используются для определения характеристик пиксела.
Если точка зрения находится не в бесконечности, алгоритм трассировки лучей лишь незначительно усложняется. Здесь предполагается, что наблюдатель по-прежнему находится на положительной полуоси z. Картинная плоскость, т. е. растр, перпендикулярна оси z, как показано на рис 3.12. Задача состоит в том, чтобы построить одноточечную центральную проекцию на картинную плоскость.
Наиболее важным элементом алгоритма определения видимых поверхностей путем трассировки лучей, является процедура определения пересечений. В состав сцены можно включать любой объект, для которого можно создать процедуру построения пересечений. Объекты сцены могут состоять из набора плоских многоугольников, многогранников или тел, ограниченных или определяемых квадратичными или биполиномиальными параметрическими поверхностями. Поскольку 75-95% времени, затрачиваемого алгоритмом трассировки лучей, уходит на определение пересечений, то эффективность процедуры поиска пересечений оказывает значительно влияние на производительность всего алгоритма. Вычислительная стоимость определения пересечений произвольной пространственной прямой (луча) с одним выделенным объектом может оказаться высокой. Чтобы избавиться от ненужного поиска пересечений, производится проверка пересечения луча с объемной оболочкой рассматриваемого объекта. И если луч не пересекает оболочки, то не нужно больше искать пересечений этого объекта с лучом. В качестве оболочки можно использовать прямоугольный параллелепипед или сферу.
3.13 Сферическая и прямоугольная оболочки
Хотя, как показано, на рис. 3.13, использование сферы в качестве оболочки может оказаться неэффективным, факт пересечения трехмерного луча со сферой определяется очень просто. В частности, если расстояние от центра сферической оболочки до луча превосходит радиус этой сферы, луч не пересекает оболочки. Следовательно, он не может пересекаться и с объектом.
Поэтому тест со сферической оболочкой сводится к определению расстояния от точки до трехмерной прямой, т. е. луча. Будем использовать параметрическое представление прямой, проходящей через точки P1(x1, y1, z1) и P2(x2, y2, z2) т. е.:
Р(t) = P1 + (P2 P1)t
с компонентами
x = x1 +(x2 x1)t = x1 +at
y = y1 +(y2 y1)t = y1 +bt
z = z1 +(z2 z1)t = z1 +ct
Тогда минимальное расстояние d от этой прямой до точки P0(x0, y0, z0) равно:
d2 = (x x0)2 + (y y0)2 +(z z0)2
а параметр t, определяющий ближайшую точку Р(t) равен:
Если d2 > R2, где R - радиус сферической оболочки, то луч не может пересечься с объектом.
Выполнение габаритного теста с прямоугольной оболочкой в трехмерном пространстве требует большого объема вычислений. При этом следует проверить пересечение луча по меньшей мере с тремя бесконечными плоскостями, ограничивающими прямоугольную оболочку. Поскольку точки пересечения могут оказаться вне граней этого параллелепипеда, то для каждой из них следует, кроме того, произвести проверку на охват или попадание внутрь. Следовательно, для трех измерений тест с прямоугольной оболочкой оказывается более медленным, чем тест со сферической оболочкой.
Одной простой процедурой можно свести тест с прямоугольной оболочкой к сравнению знаков, упрощая тем самым вычисление пересечений с объектом, а также сравнения по глубине среди точек пересечения. В этой процедуре используются переносы и повороты вокруг координатных осей для того, чтобы добиться совпадения луча с осью z. Аналогичным преобразованиям подвергается и прямоугольная оболочка объекта. Луч пересекает оболочку, если в новой перенесенной и повернутой системе координат знаки xmin и xmax, а так же ymin и ymax. противоположны, как показано на рис. 3.14.
3.14 Пересечение прямоугольной области в преобразованной системе координат
Рассмотрим упрощение вычислений точек пересечения луча и поверхности второго порядка общего вида. В произвольной декартовой системе координат поверхностей второго порядка является геометрическим местом точек, координаты которых удовлетворяют уравнению:
Q (x, y, z) = a1x2 + a2y2 + a3z2 +
b1yz + b2xz + b3xy +
c1x + c2y + c3z +d = 0
После применения преобразования, которое является комбинацией переноса и поворота и используется для совмещения луча с осью z, пересечение этого луча с поверхностью, если оно имеет место, возникает при x = y = 0. Поэтому в общем случае точки пересечения являются решениями уравнения:
т.е.
где штрих сверху обозначает коэффициенты общего уравнения поверхности второго порядка после преобразования. Если , то решения выражаются комплексными числами и луч не пересекает поверхности. Если бесконечная поверхность второго порядка (например, конус или цилиндр) ограничена плоскостями, то эти плоскости также следует преобразовать и проверить на пересечения. Если найдено пересечение с бесконечной ограничивающей плоскостью, то необходимо, кроме того, произвести проверку на попадание внутрь. Однако в преобразованной системе координат эту проверку можно произвести на двумерной проекции фигуры, образованной пересечением ограничивающей плоскости и квадратичной поверхности. Для получения точки пересечения в исходной системе координат необходимо применить обратное преобразование.
Вычисления пересечений для элементов биполиномиальных параметрических поверхностей более сложны. Уиттед предложил простой метод разбиения для элемента бикубической поверхности. Вычисления выполняются с элементом поверхности в его исходном положении. Если луч пересекает сферическую оболочку элемента поверхности, то этот кусок разбивается с помощью алгоритма разбиения предложенного Кэтмулом. Затем луч проверяется на пересечение со сферическими оболочками подэлементов. Если пересечение не обнаружено, то луч не пересекается и с самим элементом. Если же луч пересекается со сферической оболочкой какого-нибудь подэлемента, то последний разбивается дальше. Процесс завершается, если ни одна из сферических оболочек не пересечена или если достигнут заранее определенный их минимальный размер. Эти сферические оболочки минимального размера и являются искомыми пересечениями луча и элемента поверхности.
При реализации преобразования, совмещающего луч с осью z, метод разбиения можно использовать скорее применительно к прямоугольным оболочкам, чем к сферическим. Это сокращает число разбиений и увеличивает эффективность алгоритма. Для параметрических поверхностей, обладающих свойством выпуклой оболочки, например для поверхностей Безье и В-сплайнов, число разбиений можно сократить дополнительно за счет усложнения алгоритма, если для подэлементов воспользоваться их выпуклыми оболочками вместо прямоугольных.
Кадзия разработал метод для биполиномиальных параметрических поверхностей, который не требует их подразделения. Этот метод основан на понятиях, заимствованных из алгебраической геометрии. Решения получающихся при этом алгебраических уравнений высших степеней находятся численно. Метод, подобный этому, можно реализовать в преобразованной системе координат. Напомним, что биполиномиальная параметрическая поверхность определяется уравнением
Q (u, w) = 0
с компонентами
x = f (u, w)
y = g (u, w)
z = h (u, w)
в преобразованной системе координат выполнено условие x = y = 0. Значит,
f (u, w) = 0
g (u, w) = 0
Совместное решение этой пары уравнений дает значения u и w для точек пересечения. Подстановка этих значений в уравнение z = h (u, w) дает компоненту z для точек пересечения. Неудача попытки найти действительное решение означает, что луч не пересекает поверхность. Степень системы уравнений для u, w равна произведению степеней биполиномиальных поверхностей. Бикубическая поверхность, например, имеет шестую степень. Следовательно, в общем случае потребуются численные методы решения. Там, где это допустимо, для начального приближения u и w можно использовать пересечения луча с выпуклой оболочкой. Для получения пересечений в исходной системе координат, как и ранее, следует использовать обратное преобразование.
Если трассируемый луч пересекает объекты сцены в нескольких точках, то необходимо определить видимое пересечение. Для алгоритмов определения видимости простых непрозрачных поверхностей пересечением с видимой поверхностью будет точка с максимальным значением координаты z. Для более сложных алгоритмов, учитывающих отражения и преломления, эти пересечения следует упорядочить вдоль луча по расстоянию от его начала. В преобразованной системе координат этой цели можно достичь простой сортировкой по z.
Алгоритм трассировки лучей для простых непрозрачных поверхностей можно представить следующим образом:
Подготовка данных для сцены:
Создать список объектов, содержащий по меньшей мере следующую информацию:
Полное описание объекта: тип, поверхность, характеристики и т. п.
Описание сферической оболочки: центр и радиус,
Флаг прямоугольной оболочки. Если этот флаг поднят, то будет выполнен габаритный тест с прямоугольной оболочкой, если же он опушен, то тест выполняться не будет. Заметим, что габаритный тест необходим не для всех объектов, например для сферы он не нужен.
Описание прямоугольной оболочки: xmin, xmax, ymin, ymax, zmin, zmax.
Для каждого трассируемого луча:
Выполнить для каждого объекта трехмерный тест со сферической оболочкой в исходной системе координат. Если луч пересекает эту сферу, то занести объект в список активных объектов. Если список активных объектов пуст, то изобразить данный пиксел с фоновым значением интенсивности и продолжать работу. В противном случае, перенести и повернуть луч так, чтобы он совместился с осью z. Запомнить это комбинированное преобразование.
Для каждого объекта из списка активных объектов:
Если флаг прямоугольной оболочки поднят, преобразовать, используя комбинированное преобразование, эту оболочку в систему координат, в которой находится луч1 и выполнить соответствующий тест. Если пересечения с лучом нет, то перейти к следующему объекту. В противном случае преобразовать, используя комбинированное преобразование, объект в систему координат, в которой находится луч, и определить его пересечения с лучом, если они существуют. Занести все пересечения в список пересечений.
Если список пересечений пуст, то изобразить данный пиксел с фоновым значением интенсивности.
В противном случае определить z для списка пересечений.
Вычислить преобразование, обратное комбинированному преобразованию.
Используя это обратное преобразование, определить точку пересечения в исходной системе координат.
Изобразить данный пиксел, используя атрибуты пересеченного объекта и соответствующую модель освещенности.
Заметим, что алгоритм определения видимости простых непрозрачных поверхностей, не требует вычислять преобразование, обратное комбинированному, или определять точку пересечения в исходной системе координат, если в модели освещения не возникает необходимость включения в алгоритм свойств поверхности объекта или ее ориентации в точке пересечения. Эти шаги включены в данный алгоритм для полноты и удобства при реализации алгоритма трассировки лучей с учетом общей модели освещенности.
Две модификации этого простого алгоритма заметно повышают его эффективность. Первая модификация основывается на понятии кластерных групп пространственно связанных объектов. Например, предположим, что сцена состоит из стола, на котором стоят ваза с фруктами и блюдо с конфетами. В вазе лежат апельсин, яблоко, банан и груша. Блюдо содержит несколько конфет разных форм и цветов. Вводятся сферические оболочки для групп или кластеров связанных объектов, например для вазы и всех плодов в ней, для блюда и всех конфет в нем, а также для стола и всех предметов на нем. Сферические оболочки, охватывающие более чем один объект, называются сферическими кластерами. Если это необходимо, то можно ввести и прямоугольные кластеры Вводится, кроме того, наибольший сферический кластер, именуемый сферой сцены, которая охватывает все объекты в этой сцене. Затем сферические оболочки обрабатываются в иерархическом порядке. Если луч не пересекает сферу сцены, то он не может пересечь и ни одного из ее объектов. Следовательно, пиксел, соответствующий этому лучу, будет изображен с фоновым значением интенсивности. Если же луч пересекает сферу сцены, то на пересечение с лучом проверяются сферические кластеры и сферические оболочки объектов, не содержащихся ни в одном из сферических кластеров, принадлежащих кластеру сцены. Если луч не пересекает сферический кластер, то сам этот кластер и все объекты или кластеры, содержащиеся в нем, исключаются из дальнейшего рассмотрения. Если ли же луч пересекает кластер, то эта процедура рекурсивно повторяется до тех пор, пока не будут рассмотрены все объекты. Если луч пересекает сферическую оболочку некоего объекта в какой-нибудь точке, то этот объект заносится в список активных объектов. Эта процедура значительно сокращает количество вычислений точек пересечения луча со сферическими оболочками и тем самым повышает эффективность всего алгоритма.
Вторая модификация использует упорядочение по приоритет чтобы сократить число объектов, для которых вычисляются пересечения с лучом. Вместо того, чтобы немедленно производить вычисление пересечения объекта к лучом, как это делается в изложенном выше простом алгоритме, объект помещается в список пересечённых объектов. После рассмотрения всех объектов сцены преобразованный список пересеченных объектов упорядочивается по приоритету глубины. Для определения приоритетного порядка можно использовать центры сферических оболочек или наибольшие (наименьшие) значения z прямоугольных оболочек. Пересечения луча с объектами из списка пересеченных объектов определяются в порядке их приоритетов. К сожалению точка пересечения луча с первым из объектов в упорядоченном по приоритетам списке пересеченных объектов необязательно будет видимой. Необходимо определить точки пересечения луча со всеми потенциально видимыми объектами из множества {Q} и занести их в список пересечений. Затем модифицированный алгоритм упорядочивает этот список пересечений так, как это делалось и в простом алгоритме. К счастью, множество {Q} потенциально видимых объектов обычно значительно меньше числа объектов в списке пересеченных лучом. Следовательно, эффективность алгоритма возрастет. Обе эти модификации применимы также и к общему алгоритму трассировки лучей, учитывающему отражение, преломление и прозрачность.
Изложенный выше простой алгоритм не использует того обстоятельства, что некоторые грани многогранника являются нелицевыми и их можно сразу удалить, не учитывается здесь и возможная когерентность сцены. Например, несуществен порядок обработки пикселов. Вместе с тем рассмотрение этих пикселов в порядке сканирования строки развертки позволило бы воспользоваться в алгоритме когерентностью сканирующих строк. Другой подход может заключаться в подразделении сцены, причем учет когерентности областей привел бы к уменьшению числа объектов, рассматриваемых для каждого луча и, следовательно, к повышению эффективности алгоритма. Хотя использование подобных приемов повышает эффективность алгоритма определения видимости непрозрачных поверхностей их невозможно применить в общем алгоритме трассировки лучей, который учитывает отражение, преломление и прозрачность. Например, если в алгоритме учтено отражение, то объект, который полностью закрыт другим объектом, может оказаться видимым, как отражение от третьего объекта. Поскольку метод трассировки лучей является метолом грубой силы, алгоритмы определения видимости непрозрачных поверхностей, обсуждавшиеся ранее, являются более эффективными.
Д. Рот указал, что алгоритм трассировки лучей можно использовать также и для создания каркасных чертежей сплошных тел. При этом предполагается, что лучи порождаются в том порядке, в каком происходит сканирование экрана, т. е. сверху вниз и слева направо. Получающаяся процедура такова:
Если видимая поверхность для Пиксел(x, y) соответствует фону или отличается от видимой поверхности для Пиксел(x – 1 , y) или для Пиксел(x, y – 1), то изобразить этот пиксел. В противном случае пиксел не изображать.
Алгоритм трассировки лучей можно использовать, кроме того, для определения физических свойств сплошного тела. Полное рассмотрение этого вопроса не входит в эту работу. Однако для иллюстрации этого подхода приведем один пример. В частности, объем любого сплошного тела можно определить, аппроксимируя его суммой маленьких прямоугольных параллелепипедов. Это можно проделать, породив множество параллельных лучей, расположенных на определенных расстояниях друг от друга. Точки пересечения каждого луча с заданным объемом вычисляются и упорядочиваются вдоль направления этого луча. Если подвергнуть луч переносу, совмещающему его с осью z, как это было описано выше, то объем каждого прямоугольного параллелепипеда будет равен:
где lx и ly – расстояние между лучами по горизонтали и вертикали соответственно. Каждое слагаемое (zi-1 – zi) представляет собой участок луча, лежащий внутри заданного тела. Объем тела, следовательно, равен сумме объемов всех таких прямоугольных параллелепипедов. Точность результатов зависит от числа использованных лучей. Точность можно повысить, умеренно увеличив объем вычислений и рекурсивно уменьшив размер “пиксела”, в том случае, если объемы смежных прямоугольных параллелепипедов различаются более чем на заранее заданную величину. При таком подходе точнее определяются объемы тех элементов тела, где имеют место быстрые изменения, например в окрестностях ребер тел, ограниченных криволинейными поверхностями.
Ввиду внутренне присущей алгоритму трассировки лучей параллельности вычислений (здесь все лучи обрабатываются одинаково и независимо друг от друга) его можно реализовать аппаратно на основе интегральных схем с использованием методов параллельной обработки.
Резюме
В этой работе детально обсуждалось несколько основных алгоритмов, используемых для решения задачи удаления невидимых линий или поверхностей. Однако это далеко не все, что имеется. Кроме выше сказанного можно назвать алгоритм удаления невидимых линий предложенный Хеджли, который основан на использовании списка приоритетов, разбиения и построчного сканирования. Этот алгоритм работает в пространстве объекта, получает на входе выпуклые или невыпуклые многоугольники, а оценка его эффективности линейно зависит от числа объектов.
Другим примером является предложенный Азертоном интервальный алгоритм построчного сканирования, который используется для визуализации сцен, получающихся в системе конструктивного моделирования сплошных тел. Внутренний цикл этого алгоритма изменен так, чтобы можно было реализовать одномерные теоретико-множественные операции, необходимые для моделирующей системы, которая пользуется алгоритмом трассировки лучей. Азертон указывает, что этот интервальный алгоритм построчного сканирования требует примерно в 60 раз меньше времени, чем обычный алгоритм трассировки лучей.
В заключении хочу сказать, что компьютерная графика не стоит на месте. Уже давно существуют многочисленные программные и аппаратные реализации алгоритмов построения изображения. На рынке достаточно широко представлены всевозможные графические акселераторы и массивы быстрой памяти. Ведущие производители электронных компонентов поддерживают обработку изображения на уровне процессорной техники (MMX – Intel, 3D Now – AMD), следовательно, становится возможным реализация “медленных”, но дающих лучшее качество изображения алгоритмов. Отдельно следует отметить такое явления, как виртуальная реальность, которая уже в настоящее время получает широкое распространение. Одним словом, компьютерная графика будет развиваться до тех пор – пока будет развиваться и совершенствоваться компьютерная техника.

Нравится материал? Поддержи автора!
Ещё документы из категории информатика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ