Программирование в Lazarus для школьников.

Занятие № 12.

Решение квадратного уравнения.

Матыцин Игорь Владимирович

Учитель математики и информатики

МБОУ СОШ с. Девица

Цель: написать программу для решения квадратного уравнения, при любых вводных данных.

Девица 2013.

Квадратное уравнение является одним из самых распространенных уравнений школьного курса. Хотя оно решается достаточно легко, иногда требуется проверить ответы. Для этого можно использовать простую программу. Ее написание не займет много времени.

Начать нужно с самого квадратного уравнения. Из курса алгебры мы знаем, что квадратным уравнением называется уравнение вида ax²+bx+c=0, где x– переменная, a, b и с – некоторые числа, причем a.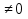

Из определения видно, что в уравнении меняются только коэффициенты a, bиc. Вот эти параметры мы и будем вводить в нашу программу, а для этого создадим три поля ввода из компонентов.

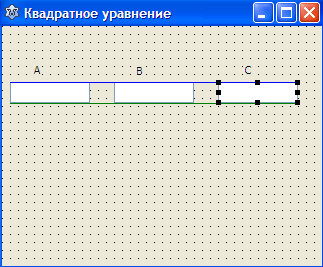
Рис 14.1 Поля ввода для коэффициентов.

Так же из определения следует, что a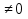. В этом случае уравнение не будет квадратным. И это условие мы будем проверять в первую очередь. Создадим кнопку «Решить» и ее разработчике событий при помощи оператора if проверим условие a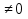. И если a=0 сообщим что наше уравнение не квадратное.

Вот обработчик событий для кнопки:

procedure TForm1.Button1Click(Sender: TObject);

var

a,b,c:real;

begin

a:=strtofloat(edit1.Text);

b:=strtofloat(edit2.Text);

c:=strtofloat(edit3.Text);

if a=0 then Label4.Caption:='Уравнение не является квадратным';

end;

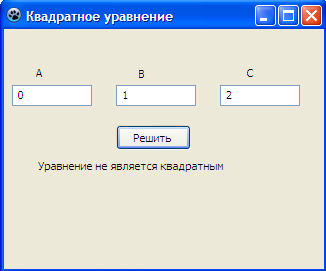
Рис. 14.2 Проверка на существование уравнения.

Теперь необходимо описать, что будет происходить, если же уравнение квадратное. Это тоже будет в том же операторе if после слова else и при использовании составного оператора.

Если уравнение квадратное, то будем сразу его решать по формуле дискриминанта и корней квадратного уравнения.

Дискриминант найдем по формуле: D:=b*b – 4*a*c;

Если дискриминант меньше нуля то уравнение не имеет решений. Это опишется так:

If d<0 then label4.Caption:=’Уравнение не имеет решений’else …

А после else пойдет непосредственный поиск корней уравнения по формулам:

X1:=(-b+sqrt(D))/2*a;

X2:=(-b-sqrt(D))/2*a;

Вот полный код оператора if:

if a=0 then Label4.Caption:='Уравнение не является квадратным' else

begin

D:=b*b-4*a*c;

if d<0 then Label4.Caption:='Уравнение не имеет решений' else

begin

X1:=(-b+sqrt(D))/2*a;

X2:=(-b-sqrt(D))/2*a;

Label4.Caption:='X1='+floattostr(x1)+' X2='+floattostr(x2);

end;

end;

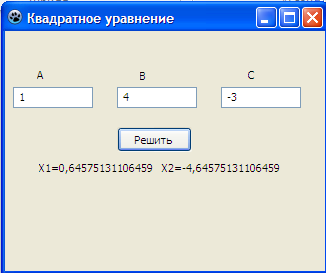
Рис. 14.3 Рабочее окне программы квадратное уравнение.