Задачник "Элементы математической логики"
Муниципальное бюджетное образовательное учреждение
дополнительного образования детей
Центр внешкольной работы
Элементы математической логики
Сборник задач
для учащихся
Разработала педагог дополнительного образования Козбан Е.В.
Межгорье
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
ЗАДАНИЯ
Задание 1.
Даны повествовательные предложения:
«У кошки 4 ноги»;
«Сумма углов треугольника равна 180°»;
«Температура кипения воды 180°»;
«У квадрата есть прямой угол»;
«2x = 3y»;
«Множество четных чисел счетно»;
«Число 5 делится на 2 без остатка»;
«x < 5»;
«У квадрата есть только один прямой угол»;
«a + b = 10»;
«Дважды два – четыре»;
«Пустое множество не имеет подмножеств».
На сколько групп и каким образом можно распределить эти предложения с точки зрения правильности сообщаемых в них сведений?
Задание 2.
Перепишите предложения из задания 1 в следующую таблицу:
Истинные
Ложные
Неопределенные (истинные или ложные в зависимости от условий)
Придумайте и внесите в таблицу еще несколько предложений каждого типа.
Задание 3.
Постройте схему, отражающую результаты проведенной классификации повествовательных предложений.
Задание 4.
Среди следующих предложений найдите истинные и ложные высказывания, предикаты:
«Земля – планета Солнечной системы»;
«Земля – самая большая планета Солнечной системы»;
«Земля вращается вокруг Солнца»;
«Земля вращается вокруг своей оси»;
«Земля вращается вокруг Солнца и вокруг своей оси»;
«Земля совершает один оборот вокруг Солнца за 24 часа»;
«Период обращения Земли вокруг Солнца составляет Т часов»;
«Среди всех фигур с одинаковым периметром наибольшую площадь имеет квадрат»;
«Может ли фигура с периметром р иметь площадь р² ?»;
«x² + y² ≥ 0»;
«Найди x, если x² = 4»;
«Зимой сутки короче, чем летом»;
«Который час?»
Задание 5.
Являются ли высказываниями следующие предложения:
«В романе «Война и мир» 3456787 слов»;
«Существует такое натуральное число, квадрат которого равен 9657847626».
Обоснуйте свое мнение.
Задание 6.
Против каждого из предикатов, приведенных в таблице, поставь знак «+» в соответствующей колонке:
Предикат
При некоторых значениях х превращается в истинное высказывание, при других – в ложное.
При любом значении х превращается в истинное высказывание.
При любом значении х превращается в ложное высказывание.
«х² < 0»
«х² > 0»
«х² ≥ 0»
«х² > 1»
«х² > х»
«х³ < 0»
«х³ > 0»
«х³ ≥ 0»
«х³ > х²»
«х² + х4 ≥ 0»
«х2 + х3 ≥ 0»
«х + 5 = 5 + х»
«х + 5 = 5 – х»
Задание 7.
Приведите несколько примеров истинных высказываний, ложных высказываний.
Задание 8.
Приведите примеры таких предикатов, которые:
а) в зависимости от значений переменных превращаются либо в истинные, либо в ложные высказывания;
б) при любых значениях переменных превращаются в истинные высказывания;
в) при любых значениях переменных превращаются в ложные высказывания.
Задание 9.
Попробуйте установить, истинными или ложными являются следующие высказывания:
а) «Число 123456789 делится без остатка на 3»;
б) «Треугольник со сторонами 4 м, 5 м и 7 м – прямоугольный»;
в) «Число 5789084 можно представить в виде произведения четырех одинаковых сомножителей»;
г) «Периметр части фигуры может быть больше периметра целой фигуры»;
д) «Во всяком треугольнике сумма длин любых двух сторон больше длины третьей стороны».
Объясните, как ты рассуждал в каждом случае.
Задание 10.
Расклассифицируй следующие предложения в соответствии с принятой нами классификацией:
а) «Квадрат любого натурального числа оканчивается на 4»;
б) «Квадрат натурального числа может оканчиваться на 4»;
в) «Квадрат натурального числа оканчивается на 4».
Задание 11.
Определи истинность следующих высказываний:
а) «Существуют числа, сумма которых больше, чем их произведение»;
б) «Не существует чисел, сумма которых больше, чем их произведение»;
в) «Сумма любых чисел меньше, чем их произведение»;
г) «Сумма любых чисел не больше, чем их произведение».
Какие из приведенных высказываний утверждают одно и то же?
Можно ли сделать заключение об истинности всех этих высказываний с помощью одного примера? Если нет, объясни, почему ты так считаешь; если да, приведи такой пример.
Задание 12.
Объедини следующие высказывания в осмысленные пары. Объясни, по какому принципу ты это сделал.
«Математическая логика – это один из разделов математики»;
«Неверно, что любой прямоугольник является квадратом»;
«Все простые числа – нечетные»;
«2 х 2 ≠ 5»;
«Математическая логика не является разделом математики»;
«Неверно, что всякое повествовательное предложение является высказыванием»;
«Любой прямоугольник – это квадрат»;
«2 х 2 = 5»;
«Всякое повествовательное предложение является высказыванием»;
«Существуют четные простые числа».
Что можно сказать об истинности высказываний, входящих в пару?
Задание 13.
Изучая теорию множеств, мы рассмотрели очень удобный способ изображения соотношений между различными множествами – диаграммы Эйлера. В математической логике есть свое средство, позволяющее наглядно изображать связь между различными высказываниями – таблицы истинности. В этих таблицах с помощью символов И и Л изображается истинность или ложность интересующего нас высказывания в зависимости от истинности или ложности других высказываний, с которыми оно связано.
Заполни таблицу истинности для отрицания высказывания А.
-
А
Ā
И
Л
Задание 14.
Для предложений из задания 4, являющихся высказываниями, сформулируй высказывания – отрицания.
Задание 15.
Для каждого высказывания, записанного курсивом, выбери из нескольких предложенных высказываний то или те, которые являются его отрицанием.
«Земля – самая близкая к Солнцу планета».
а) «Неверно, что Земля – самая близкая к Солнцу планета»;
б) «Существуют планеты, находящиеся ближе к Солнцу, чем Земля»;
в) «Земля – самая далекая от Солнца планета»;
г) «Меркурий – самая близкая к Солнцу планета»;
д) «Земля – не самая близкая к Солнцу планета».
2. «Из всех фигур с заданным периметром наибольшую площадь имеет круг».
а) «Из всех фигур с заданным периметром круг имеет наименьшую площадь»;
б) «Круг не имеет наибольшую площадь из всех фигур с заданным периметром»;
в) «Площадь круга меньше площади любой фигуры с тем же периметром»;
г) «Есть фигуры, которые имеют площадь бóльшую, чем площадь круга с тем же периметром».
3. «Любое простое число, большее 2, - нечетное».
а) «Любое составное число, большее 2, - нечетное»;
б) «Любое простое число, большее 2, - четное»;
в) «Среди простых чисел, бóльших 2, есть четные»;
г) «Неверно, что любое простое число, большее 2, - четное»;
д) «Любое простое число, меньшее 2, - нечетное».
4. «Объединение множества четных чисел и множества нечетных чисел – пустое множество».
а) «Пересечение множества четных чисел и множества нечетных чисел – пустое множество»;
б) «Объединение множества четных чисел и множества нечетных чисел не является пустым»;
в) «Пересечение множества четных чисел и множества нечетных чисел не является пустым множеством».
Задание 16.
Для каждого из высказываний, приведенных в задании 14, определи его истинность.
Задание 17.
Пусть А – некоторое высказывание.
Что представляет собой высказывание ![]() ? Заполни таблицу истинности для высказывания
? Заполни таблицу истинности для высказывания ![]() .
.
Что представляет собой высказывание ![]() ?
?
Задание 18.
Рассмотри следующие пары высказываний:
А: «Вода закипает при 100 °С»;
В: «Вода начинает замерзать при 0 °С».
А: «Вода закипает при 100 °С»;
В: «Вода начинает замерзать при 20 °С».
А: «Вода закипает при 60 °С»;
В: «Вода начинает замерзать при 0 °С».
А: «Вода закипает при 60 °С»;
В: «Вода начинает замерзать при 20 °С».
Для каждого случая попробуй из высказываний А и В с помощью союза «и» образовать новое высказывание и определить его истинность. Заполни до конца таблицу истинности:
-
А
В
А и В
И
И
И
Л
Л
И
Л
Л
Примечание: Вместо громоздких конструкций типа «Вода закипает при 100 °С и вода начинает замерзать при 0 °С» можно использовать более правильные в стилистическом отношении предложения, имеющие тот же смысл, например, «Вода закипает при 100 °С и начинает замерзать при 0 °С».
Задание 19.
Выполни задание, аналогичное заданию 18, для следующих пар высказываний:
1) А: «5 > 3»; 2) А: «-5 < 2»; 3) А: «1 < -6»; 4) А: «-8 > -3»;
В: «-4 < 2»; В: «9 < 6»; В: «-2 > -9»; В: «1 < 3».
Сравни полученную таблицу истинности с таблицей истинности для задания 18.
Задание 20.
Выполни задание, аналогичное заданию 18, для следующих пар высказываний:
А: «У всякого четырехугольника 4 угла»;
В: «У всякого четырехугольника 4 стороны».
А: «У всякого четырехугольника 4 угла»;
В: «У всякого четырехугольника 3 стороны».
А: «У всякого четырехугольника 3 угла»;
В: «У всякого четырехугольника 4 стороны».
А: «У всякого четырехугольника 3 угла»;
В: «У всякого четырехугольника 3 стороны».
Сравни полученную таблицу истинности с таблицами истинности для заданий 18 и 19.
Задание 21.
Заметил ли ты что-либо общее в результатах, полученных при выполнении заданий 18 – 20? Если да, попробуй сформулировать, что именно. Какова, на твой взгляд, «природа» этой общности?
Задание 22.
Сформулируй и обоснуй условия истинности и ложности конъюнкции трех высказываний, конъюнкции любого числа n высказываний.
Зависит ли истинность конъюнкции от очередности, в которой берутся составляющие ее высказывания?
Задание 23.
Для заданных высказываний образуй конъюнкцию и определи ее истинность:
А: «Земля планета Солнечной системы»;
В: «Луна – спутник Земли».
А: «Плотность свинца больше плотности железа»;
В: «Плотность железа меньше плотности алюминия».
А: «2 х 2 = 4»;
В: «Лондон – столица Великобритании»;
С: «Первым днем 21 века будет 1 января 2001 года».
А: «7 < 3»; В: «5 > 10».
А: «2 < 3»; В: «3 < 8».
А: «У куба 6 граней»;
В: «Все грани куба – квадраты»;
С: «Все грани куба имеют одинаковую площадь».
А: «Куб имеет 12 ребер»;
В: «Все ребра куба – отрезки одинаковой длины».
А: «У куба 8 вершин»;
В: «Расстояния между всеми вершинами куба одинаковы».
Задание 24.
Запиши высказывания, образующие следующие конъюнкции:
1)«Атмосферное давление и температура воздуха понижаются с высотой»;
2) «У треугольной пирамиды 4 грани, каждая из которых представляет собой треугольник»;
3) «Часть любой плоской фигуры всегда имеет меньшие площадь и периметр по сравнению с целой фигурой»;
4) «5 > 3 > 0»;
5) «Для любых двух множеств U и V справедливы следующие утверждения:
(U V) U, (U V) V, U (U V), V (U V) »
Что ты можешь сказать об истинности приведенных конъюнкций?
Задание 25.
Определи истинность высказывания ![]() в следующих случаях:
в следующих случаях:
М: «Я учусь в 7 классе»; N: «Мне больше 10 лет».
М: «В прошлом году я учился в 6 классе»; N: «Мне 9 лет».
М: «Я учусь в 9 классе»; N: «Мне больше 5 лет».
М: «Я учусь в 3 классе»; N: «Мне 8 лет».
Задание 26.
Дана заготовка таблицы истинности для высказывания ![]() . Заполни ее до конца, используя в качестве промежуточных данных, облегчающих работу, столбец для высказывания
. Заполни ее до конца, используя в качестве промежуточных данных, облегчающих работу, столбец для высказывания ![]() .
.
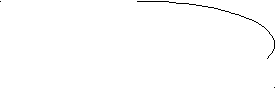

![]()
-



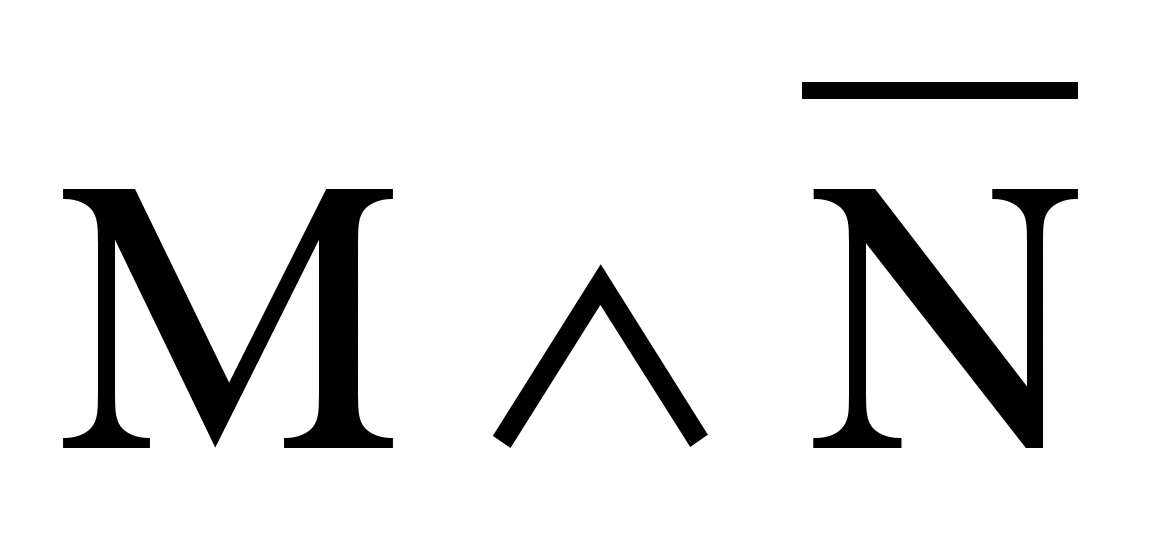
И
И
И
Л
Л
И
Л
Л
Сопоставь полученную таблицу с результатами задания 25.
Задание 27.
Построй таблицу истинности для высказывания, образуемого из высказываний М и N с помощью выражения ![]() . Чем отличается эта таблица от таблицы, полученной в задании 26?
. Чем отличается эта таблица от таблицы, полученной в задании 26?
Задание 28.
Пусть S – любое высказывание. Что можно сказать об истинности высказывания ![]() ?
?
Задание 29.
Даны высказывания:
А: «Сегодня выходной»;
В: «Я пойду гулять»;
C: «Я буду делать уроки».
Запиши с помощью буквенных выражений следующие высказывания:
«Сегодня выходной, и я пойду гулять»;
«Сегодня не выходной, и я буду делать уроки»;
«Я не пойду гулять, а буду делать уроки»;
«Сегодня выходной, но я не пойду гулять, а буду делать уроки»;
«Неверно, что я пойду гулять и не буду делать уроки».
Составь сам несколько высказываний, пользуясь высказываниями А, В, С и операциями конъюнкции и отрицания, и запиши соответствующие выражения.
Задание 30.
Какому высказыванию из задания 29 соответствует выражение ![]() ?
?
Задание 31.
Из каждой пары высказываний А, В составь новое высказывание с помощью союза «или». Определи истинность каждого полученного высказывания.
А: «Число 10 может быть представлено как 7 + 3»;
В: «Число 10 может быть представлено как 2 5»
А: «5 > 3»; В: «5 < 3». (Если определение истинности высказывания «5 > 3 или 5 < 3» вызывает у тебя затруднение, сравни это высказывание с высказыванием «5 3».
А: «Число 17 составное»;
В: «Число 17 простое».
А: «У любого прямоугольника число сторон больше числа вершин»;
В: «У любого прямоугольника число вершин больше числа сторон».
Заполни таблицу истинности для высказывания «А или В»:
-
А
В
А или В
И
И
И
Л
Л
И
Л
Л
Задание 32.
Из пар высказываний, приведенных в заданиях 18 – 20, образуй дизъюнкции. Определи их истинность.
Задание 33.
Сформулируй и обоснуй условия истинности и ложности дизъюнкции трех высказываний, дизъюнкции любого числа n высказываний. Зависит ли истинность дизъюнкции от очередности, в которой берутся составляющие ее высказывания?
Задание 34.
Высказывания А, В – истинные, а высказывания С, D – ложные. Из этих высказываний (не обязательно из всех сразу) разрешается образовывать любые конъюнкции и дизъюнкции. При этом конъюнкции и дизъюнкции, отличающиеся только порядком следования составляющих их высказываний, считаются одинаковыми.
а) Сколько различных истинных и ложных конъюнкций, истинных и ложных дизъюнкций можно образовать? Объясни, как ты считал.
б) Заполни таблицу (впиши соответствующие выражения):
Истинные
конъюнкции
Ложные
конъюнкции
Истинные
дизъюнкции
Ложные
дизъюнкции
в) Соответствуют ли данные, занесенные в таблицу, твоим расчетам?
Задание 35.
Истинны ли следующие высказывания:
1) «5 3»; 2) «7 7»; 3) «6 10»; 4) «2 2»?
Попробуй подойти к ответу с двух позиций: а) интерпретируя знаки и как «не меньше» и «не больше», б) интерпретируя эти знаки как «больше или равно» и «меньше или равно».
Задание 36.
Один семиклассник «доказал», что дизъюнкция двух ложных высказываний может оказаться истинным высказыванием. Вот его рассуждение: «Рассмотрим два высказывания – А: «Все натуральные числа – четные», В: «Все натуральные числа – нечетные». Очевидно, оба эти высказывания – ложные. Образуем высказывание с помощью союза «или»: «Все натуральные числа – четные или нечетные». Это высказывание истинное и является дизъюнкцией высказываний А и В».
Попробуй найти ошибку в этом рассуждении.
Задание 37.
Пусть S – любое высказывание. Что можно сказать об истинности высказывания ![]() ?
?
Сравни это задание с заданием 28.
Задание 38.
Из каких высказываний и с помощью каких операций образованы следующие высказывания:
«Я закончу школу в 2002 или в 2003 году»;
«Кривая линия может быть замкнутой или незамкнутой»;
«Множество рациональных чисел включает в себя множество бесконечных периодических дробей и не включает множество бесконечных непериодических дробей»;
«Число
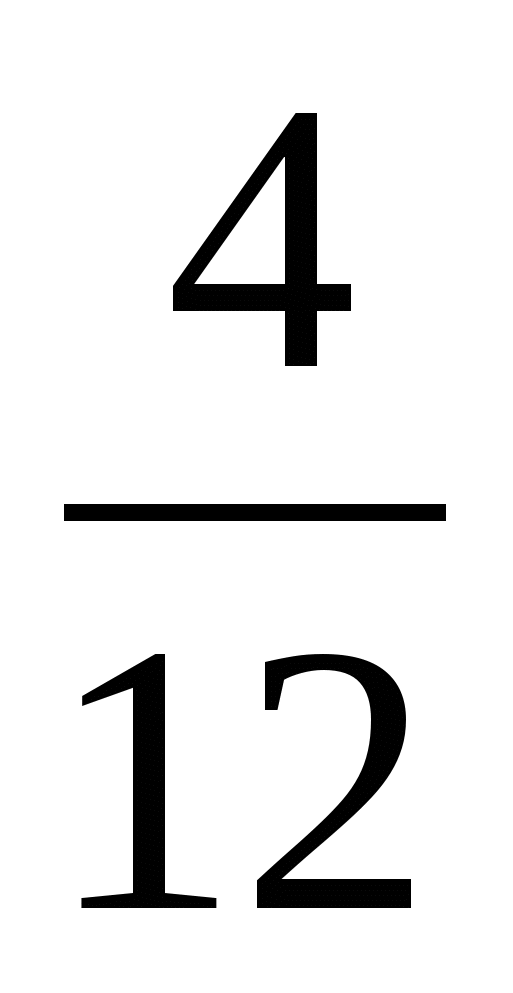 может быть представлено в виде
может быть представлено в виде 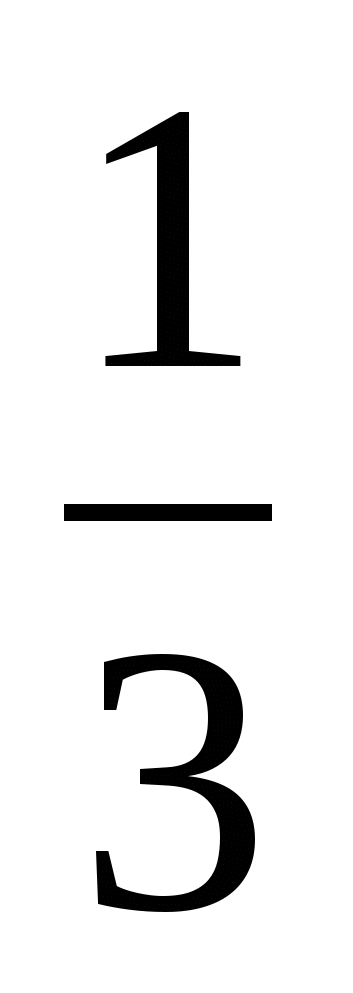 или 0,(3) и не может быть представлено в виде конечной десятичной дроби»;
или 0,(3) и не может быть представлено в виде конечной десятичной дроби»;«Квадрат можно разрезать на два треугольника или на два прямоугольника, или на треугольник и прямоугольник»;
«Через любые две точки можно провести одну прямую, но нельзя провести более одной прямой».
Определи истинность приведенных высказываний.
Задание 39.
В случае, когда интересующее нас высказывание было связано с одним исходным высказыванием (задания 13, 17), таблица истинности содержала 2 строки, не считая строки-заголовка; если рассматривалось высказывание, зависящее от двух высказываний (задания 18, 26, 31, 40, 45), таблица истинности содержала 4 строки.
Как ты думаешь, сколько строк будет в таблице истинности для высказывания, образуемого из трех исходных высказываний? Из n высказываний?
Обоснуй свое мнение.
Задание 40.
Докажи следующие формулы для высказываний:
1) А В = В А; 2) (А В) С = А (В С);
3) А В = В А; 4) (А В) С = А (В С);
5) А (В С) = (А В) (А С).
Известны ли тебе аналогичные формулы для чисел, для множеств?
Задание 41.
В мешке спрятан предмет, который имеет форму то ли шара, то ли куба, то ли цилиндра и цвет то ли красный, то ли зеленый, то ли синий. Троим мальчикам предложили заглянуть в мешок и сказать, что они там увидели. Первый сказал, что увидел синий куб, второй – зеленый шар, третий – красный цилиндр. Докажи, что, по крайней мере, один из мальчиков неправильно назвал и цвет, и форму предмета.
Задание 42.
При каких значениях переменной х приведенные ниже предикаты становятся высказываниями? При каких значениях х они превращаются в истинные высказывания, при каких – в ложные?
А (х): «х > 0»; В (х): «х2 < -7»;
С (х): «х4 0»; D (x): «![]() »;
»;
Е (х): «Натуральное число х кратно 2»;
G (х): «Школьник х является учеником седьмого класса».
Задание 43.
Дано предложение: «Предикат «![]() » не имеет смысла при х = 0». Чем оно является: предикатом, истинным или ложным высказыванием, бессмыслицей?
» не имеет смысла при х = 0». Чем оно является: предикатом, истинным или ложным высказыванием, бессмыслицей?
Задание 44.
Запиши множества истинности для предикатов из задания 49. (Стандартные обозначения числовых множеств в случае необходимости ты можешь найти в комментариях к заданиям раздела «Элементы теории множеств».)
В каких случаях для описания множеств истинности рассматриваемых предикатов целесообразно использовать способ перечисления, в каких – характеристическое свойство? Почему?
Задание 45.
Попробуй найти множества истинности для предикатов, приведенных в задании 6. В тех случаях, когда это сделать не удается, объясни причину возникших затруднений.
Задание 46.
Приведи примеры таких предикатов, для которых множество истинности:
а) совпадает с множеством определения;
б) пустое множество;
в) не совпадает с множеством определения и не является пустым множеством.
Задание 47.
Пусть Х – множество определения некоторого предиката, Т – его множество истинности, F – множество значений переменных, при которых данный предикат превращается в ложное высказывание.
Чем являются множества Т и F по отношению к множеству Х?
Вырази соотношение между множествами Х, Т и F в виде формулы и с помощью диаграммы Эйлера.
Задание 48.
Как ты думаешь, какие логические операции можно совершать над предикатами? В чем смысл этих операций? Как связаны множество определения и множество истинности предиката, получаемого в результате совершения логических операций, с соответствующими множествами исходных предикатов?
(Ограничься случаем предикатов с одной переменной и считай, что эта переменная – одна и та же для всех рассматриваемых предикатов.)
Задание 49.
Найди область определения и множество истинности для следующих предикатов и их отрицаний:
А (х): «х > 3.5»; В (у): «2у < у»;
С (n): «Натуральное число n – двузначное»;
D (z): «![]() »;
»;
E (k): «Многоугольник k имеет минимально возможное число сторон».
Для тех предикатов, переменные которых – числа, изобрази соответствующие множества на числовой прямой.
Задание 50.
Найди и изобрази на числовой прямой область определения и множество истинности для конъюнкции и дизъюнкции предикатов А (х) и В (х):
А (х): «х -5», В (х): «х 2»;
А (х): «х -1», В (х): «х 1»;
А (х): «х 3», В (х): «х 1»;
А (х): «х2 = 1», В (х): «х 0»;
А (х): «
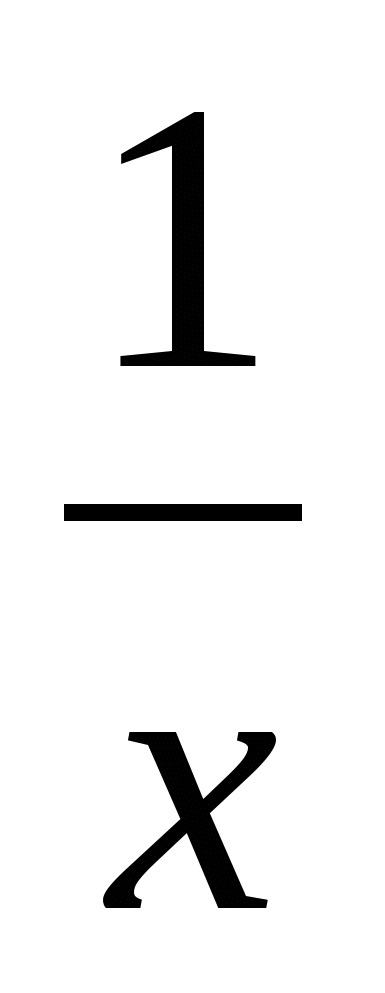 1», В (х): «х 2»;
1», В (х): «х 2»;А (х): «
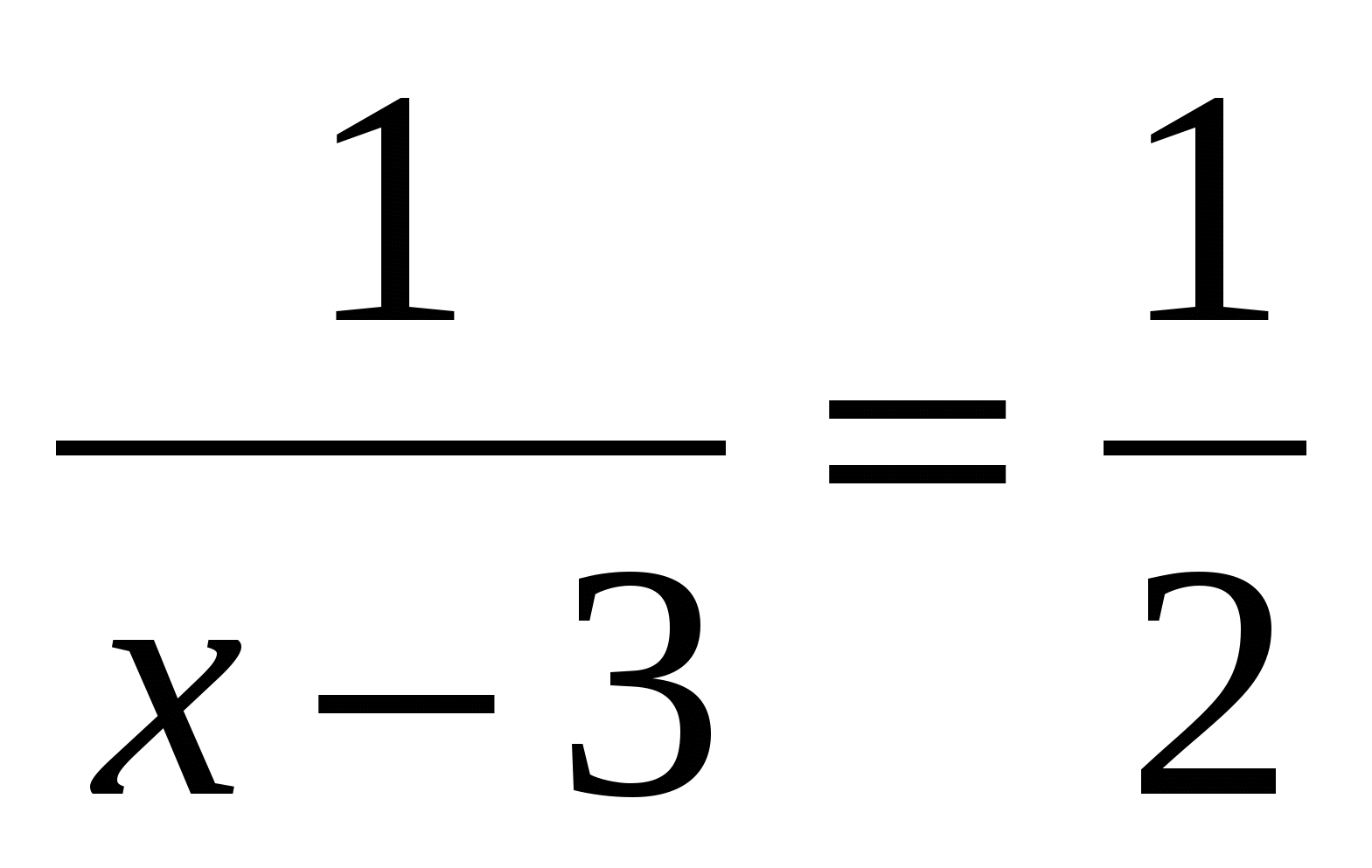 », В (х): «х = 3».
», В (х): «х = 3».
Нужно ли было, выполняя это задание, искать отдельно области определения для конъюнкции и дизъюнкции?
Сравни это задание с заданием 128 из раздела «Элементы теории множеств».
Придумай сам несколько заданий подобного типа.
Задание 51.
На множестве Х = {1; 2; 6,3; 7; 12,5; 15} заданы два предиката:
А: «х 3» и В: «1 х 12».
Найди множество истинности ![]() предиката А и множество истинности
предиката А и множество истинности ![]() предиката В.
предиката В.
Найди множество истинности ![]() предиката А В и множество истинности
предиката А В и множество истинности ![]() предиката А В.
предиката А В.
Задание 52.
В задании 45 была рассмотрена импликация высказываний. Импликация Р Q высказываний Р и Q ложна, если Р истинно, а Q ложно, и истинна во всех других случаях.
Пусть А (х) и В (х) – два предиката, имеющие одно и то же множество определения Х и множества истинности ![]() и
и ![]() соответственно. Попробуй сформулировать, что представляет собой импликация предикатов А (х) В (х), и записать формулу для множества истинности
соответственно. Попробуй сформулировать, что представляет собой импликация предикатов А (х) В (х), и записать формулу для множества истинности ![]() (выразить
(выразить ![]() через Х,
через Х, ![]() и
и ![]() ).
).
Изобрази множества Х, ![]() ,
, ![]() и
и ![]() на диаграмме Эйлера.
на диаграмме Эйлера.
Задание 53.
В одной из школ в 7 «Ы» классе действует такое расписание уроков:
Понедельник
Вторник
Среда
Четверг
Пятница
Суббота
1
Русский яз.
Физика
Англ. яз.
Физика
Биология
Физ-ра
2
Алгебра
Химия
Алгебра
Алгебра
География
Русск. яз.
3
Физ-ра
Алгебра
Физ-ра
Литература
Алгебра
Живопись
4
Англ. яз.
Геометрия
Русский яз.
Русский яз.
Геометрия
Труд
5
История
Литература
Биология
Химия
Литература
6
География
Англ. яз.
История
7
Труд
Какой из знаков , , , по-твоему, следует поставить вместо многоточия, чтобы правильно и наиболее полно отразить взаимосвязь между приведенными ниже утверждениями? Почему ты так считаешь?
«Сегодня понедельник» … «Сегодня 5 уроков»;
«Сегодня вторник» … «Сегодня первый урок – физика»;
«Сегодня среда» … «Сегодня пятый урок – биология»;
«Сегодня есть география» … «Сегодня вторник»;
«Сегодня есть геометрия» … «Сегодня вторник или пятница»;
«Сегодня шесть уроков» … «Сегодня второй урок – химия»;
«Сегодня четвертый урок – труд» … «Сегодня суббота»;
«Сегодня есть история и нет физкультуры» … «Сегодня есть литература и алгебра»;
«Сегодня на один урок меньше, чем было вчера» … «Сегодня есть биология»;
«Сегодня нет истории» … «Сегодня есть алгебра».
Придумай еще несколько утверждений, связанных знаками исходя из этого же расписания уроков.
Разработай аналогичное задание на основе реального расписания уроков в твоем классе.
Как можно переписать соотношения между утверждениями, в которых используется знак , в более употребительной форме – используя знак ?
Задание 54.
Исходя из расписания уроков, приведенного в задании 60, впиши вместо многоточий подходящие утверждения (утверждение должно быть не просто правильным, а наиболее полно соответствовать указанному знаку):
«Сегодня четверг» ;
«Сегодня четверг» ;
«Сегодня третий урок – алгебра»;
«Сегодня третий урок – алгебра»;
«Сегодня второй урок – алгебра, а третий – физкультура» ;
«Сегодня второй урок – алгебра, а третий – физкультура» ;
«Сегодня нет ни физики, ни географии»;
«Сегодня нет ни физики, ни географии».
Придумай и выполни еще несколько заданий подобного типа.
Задание 55.
Изобрази логическую связь между утверждениями ![]() и
и ![]() в символьной форме:
в символьной форме:
1) ![]() : «Число х делится без остатка на 4»,
: «Число х делится без остатка на 4»,
![]() : «Число х – четное»;
: «Число х – четное»;
2) ![]() : «Четырехугольник АВСD – квадрат»,
: «Четырехугольник АВСD – квадрат»,
![]() : «У четырехугольника ABCD А = В = С = D
: «У четырехугольника ABCD А = В = С = D
и АВ = ВС = CD = DA»;
3) ![]() : «а b =0»,
: «а b =0», ![]() : «a = 0»;
: «a = 0»;
4) ![]() : «m < 0 и n < 0»,
: «m < 0 и n < 0», ![]() : «m n > 0 и m + n < 0».
: «m n > 0 и m + n < 0».
Задание 56.
Вместо многоточий подставь нужные термины – «необходимо», «достаточно», «необходимо и достаточно»:
1) «Для того, чтобы число делилось на 9, …, чтобы его сумма цифр делилась на 9»;
2) «Для того, чтобы число делилось на 9, …, чтобы его сумма цифр делилась на 3»;
3) «Для того, чтобы число делилось на 3, …, чтобы его сумма цифр делилась на 9»;
4) «Для того, чтобы число делилось на 3, …, чтобы его сумма цифр делилась на 3»;
5) «Для того, чтобы число делилось на 5, …, чтобы его сумма цифр делилась на 5»;
6) «Для того, чтобы у прямой было две общих точки с окружностью, …, чтобы прямая проходила через центр окружности»;
7) «Для того, чтобы две окружности разного радиуса не имели общих точек, …, чтобы расстояние между их центрами было больше суммы радиусов»;
8) «Для того, чтобы две окружности одинакового радиуса не имели общих точек, …, чтобы расстояние между их центрами было больше суммы радиусов»;
9) «Для того, чтобы два шара не имели общих точек, …, чтобы расстояние между их центрами было больше суммы их радиусов»;
10) «Для того, чтобы пересечение двух множеств совпадало с одним из этих множеств, …, чтобы одно из множеств было подмножеством другого».
Задание 57.
Дано утверждение: «Для того, чтобы произведение нескольких чисел было равно 0, необходимо и достаточно, чтобы хотя бы один из сомножителей был равен 0». Переформулируй его, заменяя слова «необходимо и достаточно» эквивалентными терминами.
Задание 58.
Для каких из приведенных ниже утверждений верны и обратные утверждения? Как они формулируются? Для этих случаев сформулируй утверждение, включающее одновременно и прямое и обратное утверждения, пользуясь термином «необходимо и достаточно» или эквивалентными терминами.
«Если число делится на 12, то оно делится на 4 и на 3»;
«Если число делится на 8, то оно делится на 4 и на 2»;
«Если число оканчивается тремя нулями, то оно делится на 1000»;
«Если число оканчивается четырьмя нулями, то оно делится на 1000»;
«Сфера радиуса
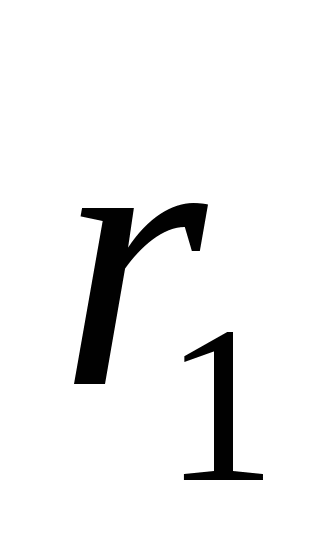 может быть помещена внутрь сферы радиуса
может быть помещена внутрь сферы радиуса 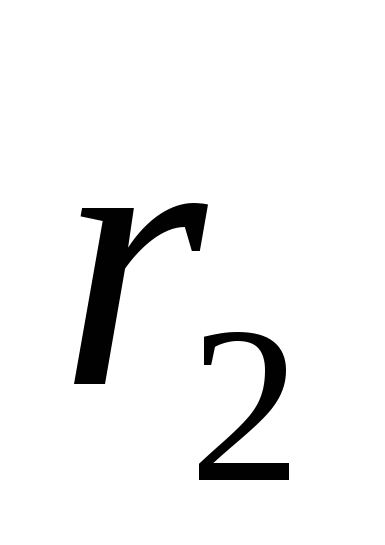 , если
, если 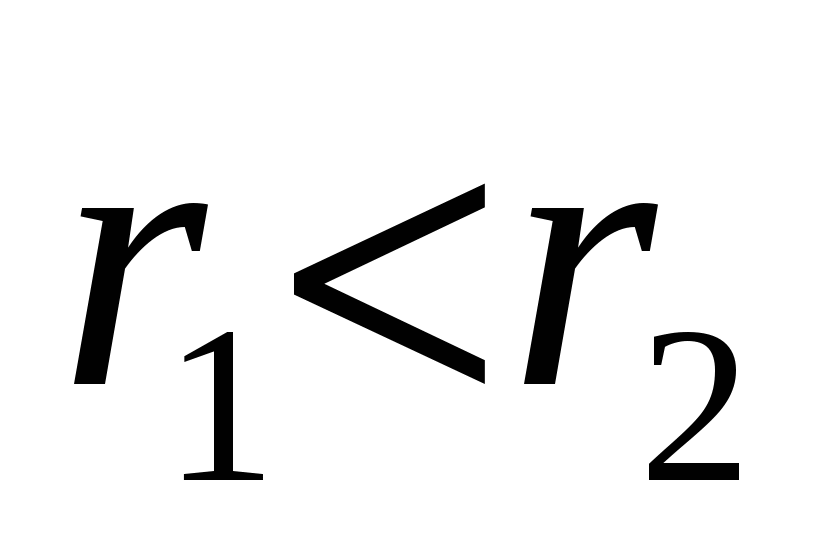 »;
»;«Если a = b, то a + c = b + c»;
«Если a = b, то a c = b c»;
«Сумма любых двух отрицательных чисел – отрицательное число»;
«Никакое число, оканчивающееся на 2, не является квадратом натурального числа».
Сформулируй несколько утверждений таких, для которых обратные утверждения верны, и таких, для которых обратные утверждения не верны.
Задание 59.
Сформулируй известные тебе признаки делимости, пользуясь термином «необходимо и достаточно» и эквивалентными ему терминами.
Попробуй сформулировать и обосновать признак делимости на 6.
Задание 60.
«Нет дыма без огня». Каким условием – необходимым или достаточным – является утверждение о наличии дыма для того, чтобы утверждать о наличии огня, если следовать этой пословице?
Задание 61.
Составь несколько заданий, которые способствовали бы освоению понятий необходимости и достаточности.
КОММЕНТАРИИ К ЗАДАНИЯМ
Задание __.
Тебя не смутила запись некоторых предложений в виде математических формул? Формула тоже может быть истолкована как предложение. Например, формула p ּ q = 5 может быть прочитана как «Произведение чисел p и q равно 5».
А теперь – по существу задания. С точки зрения справедливости сообщаемых сведений приведенные в задании предложения могут быть разделены на 3 группы:
1) предложения, которые содержат истинные сведения;
2) предложения, которые содержат ложные сведения;
3) предложения, содержащие такие сведения, которые при определенных условиях оказываются истинными, а при других условиях - ложными.
Например, предложение «Сумма углов треугольника равна 180˚» - истинное, предложение «Пустое множество не имеет подмножеств» - ложное (объясни, почему), а предложение «а + b = 10» может быть истинным или ложным в зависимости от того, какие числовые значения принимают буквы а и b.
К тем же группам может отнесено и большинство других повествовательных предложений.
Задание __.
Итак, все повествовательные предложения, которые мы рассмотрели, и многие другие можно отнести к одному из трех типов: истинные, ложные или ложные в зависимости от условий. Такие предложения и являются объектом изучения математической логики. Причем с точки зрения математической логики конкретное содержание предложения не имеет значения. Важно только, к какому типу истинности оно может быть отнесено. Законы математической логики позволяют конструировать сложные предложения из простых или, наоборот, анализировать структуру сложных предложений, устанавливать их истинность, исходя из истинности их составных частей. Кстати, такой принцип абстрагирования, или отвлечения от конкретных, но второстепенных с точки зрения данной теории свойств объектов типичен для математики. Человечество сделало огромный шаг вперед, когда люди научились считать предметы независимо от их конкретного вида. Теория множеств точно так же не интересуется конкретным предметным составом множеств, а концентрирует внимание на их отношениях. Геометрия возникла из задач измерения земельных участков (об этом говорит ее название), но потом стала развиваться по своим собственным законам. Благодаря такому абстрагированию результаты математических теорий обладают поразительной общностью и универсальностью и, хотя не сразу, находят подтверждение и применение в реальном мире.
Возможно, рассмотренная классификация предложений кажется тебе слишком упрощенной и условной. Ведь иногда бывает трудно – практически невозможно – однозначно установить истинность или ложность того или иного утверждения, допустим, такого: «Математическая логика – самая интересная область математики». Такие ситуации привели к появлению новых разделов логики,
В которых различным утверждениям может приписываться и та или иная промежуточная степень истинности (например, «почти достоверно», «возможно», «сомнительно» и т.п.), а не только крайние значения – «истинно» или «ложно». Конечно, такая многозначная логика оказывается значительно сложнее классической двузначной логики, пользующей только понятиями «истинно» и «ложно», зато она обладает и большими возможностями при описании реальных ситуаций. Однако, и «обычная» двузначная логика находит очень широкое применение, в частности, как теория искусства правильного рассуждения, теория математических доказательств, а также как одно из теоретических оснований компьютерной техники.
Но вернемся к рассматриваемым предложениям. Предложения первых двух типов, т.е. такие повествовательные предложения, о которых можно сказать истинны они или ложны, называются высказываниями.
В математической логике принято обозначать высказывания заглавными буквами. Например,
А: «Волга – это озеро в Африке»; ![]()
Предложения третьего типа, не являются высказываниями, но их можно превратить в высказывания, заменив буквы, обозначающие числа, конкретными числовыми значениями. Например, предложение «х – четное число» при х = 8 превращается в истинное высказывание, а при х = 11 – в ложное. В таких предложениях мы можем изменять конкретные числовые значения, соответствующие буквам, получая каждый раз вполне определенное высказывание. Поэтому буквы в таких предложениях называются переменными, а сами повествовательные предложения такого типа называются высказываниями с переменными (высказывательными формами, предикатами).
Следует отметить, что переменные в предикате могут быть не только числовыми. Например, предложение «Учащийся х – отличник» является предикатом. Подставляя в него вместо х фамилии конкретных учащихся, мы будем получать истинные или ложные высказывания.
Для обозначения предикатов используют заглавные буквы, а переменные, входящие в предикат, указываются в скобках. Например, С (х): «х - четное число»; D(х, y): ![]()
Нужно обратить внимание на следующую тонкость. Основным отличительным признаком предиката является именно наличие одной или нескольких переменных. Чаще всего это приводит к тому, что один и тот же предикат в зависимости от значений переменных может превращаться либо в истинное, либо в ложные высказывание. Но это не обязательно. Например, предложение «![]() » - это предикат, так как u может принимать различные числовые значения. Тем не менее, при подстановке вместо u любого действительного числа получается только истинное высказывание. От этого предиката нужно отличать предложение «Для любого действительного u выполняется неравенство «
» - это предикат, так как u может принимать различные числовые значения. Тем не менее, при подстановке вместо u любого действительного числа получается только истинное высказывание. От этого предиката нужно отличать предложение «Для любого действительного u выполняется неравенство «![]() ». Это – не предикат, а истинное высказывание. Ведь в данное предложение нельзя вместо u подставить какое-нибудь число, например, 5. Получится бессмысленный набор слов: «Для любого действительного числа 5…»
». Это – не предикат, а истинное высказывание. Ведь в данное предложение нельзя вместо u подставить какое-нибудь число, например, 5. Получится бессмысленный набор слов: «Для любого действительного числа 5…»
Задание __.
Классификация повествовательных предложений может быть представлена в виде такой схемы:

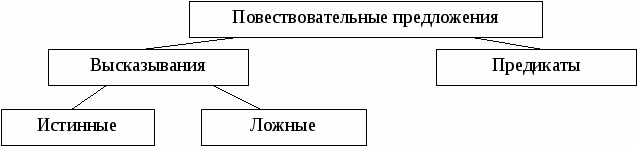
Задание __.
Предложение «В романе “Война и мир” 3456787 слов» - высказывание, ведь оно наверняка либо истинно, либо ложно, хотя для того, чтобы установить, какое оно, нужно проделать большую и вряд ли достаточно осмысленную работу.
Точно также высказыванием является предложение под номером 2, хотя установить, истинно оно или ложно, тоже не очень просто.
Задание __.
Высказывание д) представляет собой одну из важнейших теорем геометрии – так называемое «неравенство треугольника». Со строгим доказательством этой теоремы ты скоро познакомишься в курсе геометрии. А сейчас мы просто проиллюстрируем ее.
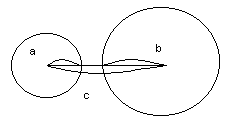
Как можно построить треугольник, если заданы три его стороны:a, b, c?
Отложим отрезок, равный одной из сторон, например, с. Тем самым мы определим две вершины треугольника, которые совпадают с концами отрезка с. Третья вершина должна находиться на расстоянии а от одного из концов отрезка с и на расстоянии b от другого конца. Другими словами, эта вершина должна находиться на пересечении окружностей радиусов а и b, центры которых находятся в концах отрезка с. Если окружности пересеклись, в качестве вершины можно выбрать любую из точек пересечения.
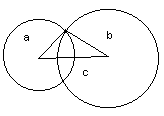
А теперь покажем, что при a + b ≤ c никакого треугольника не получится.
Если a + b = c, то окружности только коснуться друг друга в точке, которая лежит на отрезке с. Вершина как бы «упала» на противоположную сторону. Треугольник не получился. (Иногда такую фигуру называют вырожденным треугольником.)
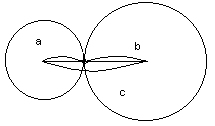
Если же a+b<c, окружности вообще не будут иметь общих точек, следовательно, треугольника с такими сторонами не существует.
Задание __.
Предложение «Квадрат любого натурального оканчивается на 4» - ложное высказывание.
Предложение «Квадрат натурального числа может оканчиваться на 4» - истинное высказывание. По-другому оно может быть сформулировано так: «Существуют натуральные числа, квадрат которых оканчивается на 4».
Предложение «Квадрат натурального числа оканчивается на 4» - предикат, хотя буквенное обозначение переменной отсутствует. В зависимости от того, о каком натуральном числе идет речь, данное предложение может превратиться в истинное или ложное высказывание. Данное предложение можно заменить, например, таким: «Младший разряд числа n2 равен 4», которое, очевидно, является предикатом.
Задание __.
Все приведенные в задании высказывания могут быть объединены в пары, в каждой из которых одно высказывание отрицает другое. Если некоторое высказывание получается из высказывания А с помощью утверждения, что А неверно, то это новое высказывание называют отрицанием А. Такое высказывание обозначается ![]() . Кстати, мы и раньше использовали черту в качестве символа отрицания. Вспомни, например, значок
. Кстати, мы и раньше использовали черту в качестве символа отрицания. Вспомни, например, значок ![]() или обозначение для дополнения множества.
или обозначение для дополнения множества.
Под отрицанием понимают также логическую операцию над высказыванием А, приводящую к высказыванию ![]() .
.
Из двух высказываний А и ![]() одно обязательно является истинным, а другое – ложным. Это утверждение представляет собой так называемый закон исключенного третьего.
одно обязательно является истинным, а другое – ложным. Это утверждение представляет собой так называемый закон исключенного третьего.
Наиболее универсальный способ образования ![]() - это формирование высказывания «Неверно, что А». Например, если А: « 5 больше 3», то
- это формирование высказывания «Неверно, что А». Например, если А: « 5 больше 3», то ![]() : «Неверно, что 5 больше 3». Но это не единственный способ. Например, то же самое высказывание
: «Неверно, что 5 больше 3». Но это не единственный способ. Например, то же самое высказывание ![]() может быть сформулировано с помощью частицы не: «5 не больше 3». (Обрати внимание: отрицанием для высказывания «5 > 3» является именно высказывание «5 ≤ 3», а не «5 < 3».)
может быть сформулировано с помощью частицы не: «5 не больше 3». (Обрати внимание: отрицанием для высказывания «5 > 3» является именно высказывание «5 ≤ 3», а не «5 < 3».)
И все-таки стоит иметь в виду, что попытка сразу образовать отрицание с помощью частицы не в сложных случаях может привести к ошибке. Например, из высказывания К: «Все числа, кратные 3, кратны 9» с помощью частицы не можно образовать 3 высказывания, имеющих различный смысл: «Не все числа, кратные 3, кратны 9», «Все числа, не кратные 3, кратны 9», «Все числа, кратные 3, не кратны 9». Какое же из этих высказываний является отрицанием высказывания К? Все станет ясным, если мы сначала сформулируем отрицание в форме «Неверно, что К».![]() : «Неверно, что все числа, кратные 3, кратны 9». Из трех приведенных выше высказываний такой же смысл имеет только высказывание «Не все числа, кратные 3, кратны 9». Значит, оно и является отрицанием высказывания К. Кстати, высказывание
: «Неверно, что все числа, кратные 3, кратны 9». Из трех приведенных выше высказываний такой же смысл имеет только высказывание «Не все числа, кратные 3, кратны 9». Значит, оно и является отрицанием высказывания К. Кстати, высказывание ![]() может быть сформулировано и так: «Существуют числа, кратные 3, которые не кратны 9».
может быть сформулировано и так: «Существуют числа, кратные 3, которые не кратны 9».
Наряду с операцией отрицания в математической логике рассматриваются и другие операции над высказываниями, с которыми ты скоро познакомишься. Эти операции над высказываниями, с которыми ты скоро познакомишься. Эти операции во многом похожи на арифметические действия и операции над множествами. Изучением логических операций над высказываниями занимается раздел математической логики, который называется алгеброй логики. Основатель алгебры логики – Дж. Буль.
Задание __.
У тебя должна получиться такая таблица истинности:
-
А

И
Л
Л
И
Эту таблицу истинности наряду с приведенной выше словесной формулировкой можно рассматривать в качестве определения отрицания. Использование таблицы истинности может помочь в не совсем очевидных ситуациях, например, такой: можно ли считать высказывание «Сегодня понедельник» отрицанием высказывания «Сегодня четверг»? Из таблицы истинности следует, что нельзя, поскольку эти высказывания могут быть одновременно ложными. Отрицанием высказывания «Сегодня четверг» является только высказывание «Неверно, что сегодня четверг» или высказывания, имеющие точно такой же смысл, например, «Сегодня не четверг».
Задание __.
Рассмотрим некоторые наиболее сложные случаи.
Хотя высказывания А: «Земля – самая близкая к Солнцу планета» и В: «Меркурий – самая близкая к Солнцу планета» близки по содержанию и первое из них ложно, а второе истинно, В не является отрицанием А. Ведь ![]() должно строиться по определенным правилам из А, а в А не идет речь о Меркурии.
должно строиться по определенным правилам из А, а в А не идет речь о Меркурии.
Для высказывания «Любое простое число, большее 2, - нечетное», очевидно, является отрицанием отсутствующее среди предложенных высказывание «Неверно, что любое простое число, большее 2, - нечетное». Из приведенных в задании высказываний такой же смысл имеет только высказывание «Среди простых чисел, больших 2, есть четные». Оно и является отрицанием.
Задание __.
Составим таблицу истинности, последовательно двигаясь от исходного высказывания А к его двойному отрицанию ![]() :
:
-
А

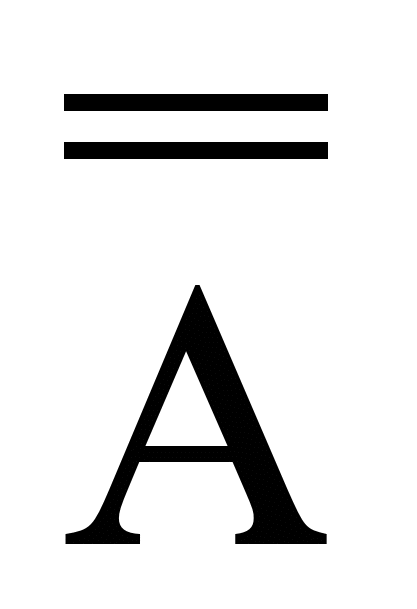
И
Л
И
Л
И
Л
Из таблицы следует, что в результате двойного отрицания из истинного высказывания получается истинное высказывание, а из ложного – ложное. Таким образом, двойное отрицание всегда приводит к исходному высказыванию. Впрочем, этот результат достаточно очевиден и без таблицы истинности. Но такой прием – поэтапный переход от истинного или нескольких исходных высказываний к окончательному – является достаточно универсальным, и мы будем часто пользоваться им, когда освоим другие, более сложные операции над высказываниями.
Один из основоположников логики Аристотель предложил систему логических правил, так называемых силлогизмов. Некоторые из них звучат примерно так: «друг моего друга – мой друг», «враг моего друга – мой враг», «друг моего врага – мой враг», «враг моего врага мой друг». С современной точки зрения мы бы могли назвать такие правила моделью логических заключений. Как ты думаешь, какой из приведенных силлогизмов можно считать моделью двойного отрицания
Задания ____.
Хотя в заданиях 18 -20 рассматривались высказывания, не имеющие ничего общего по содержанию (свойства воды, числовые неравенства, свойства четырехугольников), ты, наверное, обратил внимание на одну важную закономерность. Высказывание, образуемое с помощью союза «и» из двух других высказываний, истинно в единственном случае – когда истинны оба исходных высказывания. (Вместо «истинно в единственном случае» математики говорят более строго: «истинно тогда и только тогда». Попробуй объяснить смысл этого выражения. См. также задание 41 из раздела «Элементы теории множеств». Чуть позже мы специально рассмотрим с логической точки зрения выражения такого типа.)
Высказывание, образуемое из высказываний А и В с помощью союза «и», называют конъюнкцией высказываний А, В. Конъюнкцию высказываний А, В принято обозначать А ![]() В или А & В.
В или А & В.
Под конъюнкцией понимают также логическую операцию над высказываниями, состоящую в образовании нового высказывания с помощью союза «и».
Таблица истинности для конъюнкции (она должна была получиться у тебя одной и той для заданий 18 – 20) выглядит так:
-
А
В
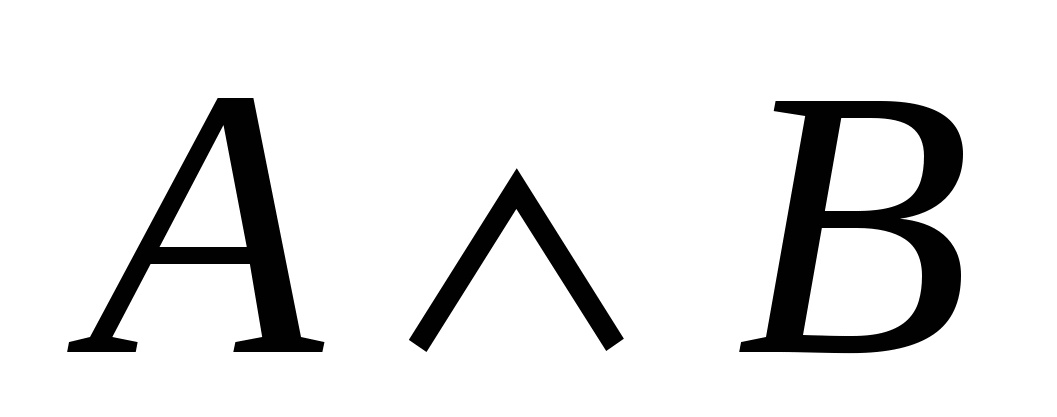
И
И
И
И
Л
Л
Л
И
Л
Л
Л
Л
Естественно, понятие конъюнкции может быть обобщено на любое количество высказываний. Например, запись ![]() означает, что из высказываний Е и F образуется
означает, что из высказываний Е и F образуется ![]() , затем из высказываний
, затем из высказываний ![]() и G образуется высказывание
и G образуется высказывание ![]() и, наконец, из высказываний
и, наконец, из высказываний ![]() и H образуется высказывание
и H образуется высказывание ![]() .
.
В ряде случаев высказывание, представляющее собой конъюнкцию нескольких высказываний, может быть переформулировано так, что оно не будет дословно повторять исходные высказывания, связанные союзом «и». Например, конъюнкция высказываний «Через любые две точки можно провести прямую» и «Ни через какие две точки нельзя провести более одной прямой» может быть сформулировано следующим образом: «Через любые две точки можно провести прямую, притом только одну». Последнее высказывание представляет собой важнейшую аксиому геометрии – так называемую «аксиому прямой». Эта аксиома утверждает сразу два факта: существование прямой, проходящей через любые две заданные точки, и единственность такой прямой.
В русском языке вместо союза «и» часто используют союзы «а», «но» и другие, которые могут придавать предложениям различные смысловые оттенки, но с точки зрения истинности образуемых с помощью этих союзов высказываний эти оттенки несущественны.
Задание __.
Пусть имеется n высказываний: ![]() Если последовательно образовывать конъюнкцию этих высказываний, поочередно добавляя все новые и новые высказывания, мы будем получать истинное высказывание до тех пор, пока среди заданных высказываний не встретится первое ложное. С этого момента конъюнкция станет ложным высказыванием, и добавление любых других высказываний, независимо от их истинности, не сможет превратить ее в истинное высказывание. Если среди высказываний
Если последовательно образовывать конъюнкцию этих высказываний, поочередно добавляя все новые и новые высказывания, мы будем получать истинное высказывание до тех пор, пока среди заданных высказываний не встретится первое ложное. С этого момента конъюнкция станет ложным высказыванием, и добавление любых других высказываний, независимо от их истинности, не сможет превратить ее в истинное высказывание. Если среди высказываний ![]() нет ни одного ложного, то на каждом шаге, до самого последнего включительно, будет получаться истинное высказывание. Таким образом, конъюнкция n высказываний является истинным высказыванием, если все эти п высказываний истинны, и ложным, если среди данных n высказываний есть хотя бы одно ложное.
нет ни одного ложного, то на каждом шаге, до самого последнего включительно, будет получаться истинное высказывание. Таким образом, конъюнкция n высказываний является истинным высказыванием, если все эти п высказываний истинны, и ложным, если среди данных n высказываний есть хотя бы одно ложное.
Задание __.
На первый взгляд странным может показаться случай под номером 3. Высказывания А, В и С никак не связаны друг с другом смысловым содержанием, поэтому возникает вопрос, правомерно ли вообще говорить о конъюнкции этих высказываний. Но ты уже хорошо представляешь себе, что для математической логики имеет значение только истинность высказываний, а не их содержание. Поэтому постановка вопроса в задании вполне правомерна, а конъюнкция ![]() С является истинным высказыванием, поскольку каждое из высказываний А, В, С истинно.
С является истинным высказыванием, поскольку каждое из высказываний А, В, С истинно.
Конъюнкция высказываний, приведенных под номером 5, может быть записана в виде двойного неравенства: «2< 3 < 8».
Конъюнкция высказываний под номером 6 может быть сформулирована и таким образом: «У куба 6 граней, которые представляют собой квадраты одинаковой площади».
Задание __.
Высказывание, образуемое из высказываний А и В с помощью союза «или», называют дизъюнкцией высказываний А, В. Дизъюнкцию высказываний А, В принято обозначать ![]()
Под дизъюнкцией понимают также логическую операцию над высказываниями, состоящую в образовании нового высказывания с помощью союза «или».
В обычной речи союз «или» может пониматься с различными оттенками. Поэтому приведенное выше определение дизъюнкции нуждается в конкретизации. В математической логике считается, что дизъюнкция ![]() истинна, если истинно хотя бы одно из высказываний А, В. Соответствующая таблица истинности имеет вид:
истинна, если истинно хотя бы одно из высказываний А, В. Соответствующая таблица истинности имеет вид:
-
А
В
А или В
И
И
И
И
Л
И
Л
И
И
Л
Л
Л
Понятие дизъюнкции может быть обобщено на любое количество высказываний. Например, запись ![]() означает, что из высказываний К и L образуется высказывание
означает, что из высказываний К и L образуется высказывание ![]() , затем из высказываний
, затем из высказываний ![]() и М образуется высказывание
и М образуется высказывание ![]() и, наконец, из высказываний
и, наконец, из высказываний ![]() и N образуется высказывание
и N образуется высказывание ![]() .
.
Задание __.
Дизъюнкция n высказываний является истинным высказыванием, если среди этих n высказываний есть хотя бы одно истинное, и ложным, если все n высказываний – ложные. Если обоснование этого факта вызывает у тебя затруднение, посмотри комментарий к заданию 22.
Задание __.
Если смысл знаков ![]() и
и ![]() выражать словами «не меньше» и «не больше», то можно заключить, что все приведенные высказывания истинные, как отрицания ложных высказываний. Например, высказывание «
выражать словами «не меньше» и «не больше», то можно заключить, что все приведенные высказывания истинные, как отрицания ложных высказываний. Например, высказывание «![]() » - отрицание ложного высказывания «7< 7» и, следовательно, истинно.
» - отрицание ложного высказывания «7< 7» и, следовательно, истинно.
Если смысл знаков ![]() и
и ![]() выражать словами «больше или равно» и «меньше или равно», то все приведенные высказывание истинные, как дизъюнкции истинного и ложного высказываний. Например, то же высказывание «
выражать словами «больше или равно» и «меньше или равно», то все приведенные высказывание истинные, как дизъюнкции истинного и ложного высказываний. Например, то же высказывание « ![]() » представляет собой дизъюнкцию ложного высказывания «7 > 7» и истинного высказывания «7 = 7» и, следовательно, истинно.
» представляет собой дизъюнкцию ложного высказывания «7 > 7» и истинного высказывания «7 = 7» и, следовательно, истинно.
Задание __.
Образуем дизъюнкцию ![]() строго по правилам: «Все натуральные числа – четные или все натуральные числа – нечетные». Поскольку никакое число не может быть четным и нечетным одновременно, это высказывание утверждает, что либо все натуральные числа – четные, либо все натуральные числа – нечетные. Очевидно, это высказывание – ложное, что согласуется со свойствами дизъюнкции.
строго по правилам: «Все натуральные числа – четные или все натуральные числа – нечетные». Поскольку никакое число не может быть четным и нечетным одновременно, это высказывание утверждает, что либо все натуральные числа – четные, либо все натуральные числа – нечетные. Очевидно, это высказывание – ложное, что согласуется со свойствами дизъюнкции.
Теперь рассмотрим предложение «Все натуральные числа – четные или нечетные». Его можно понять и в том смысле, что «не существует натуральных чисел, не являющихся ни четными, ни нечетными». Это истинное утверждение (его можно рассматривать как одно из проявлений закона исключенного третьего – всякое натуральное число либо делится на 2, либо не делится), но оно не является дизъюнкцией высказываний «Все натуральные числа – четные» и «Все натуральные числа – нечетные».
Рассмотренный пример показывает, что одни и те же предложения, сформулированные на естественном языке, могут пониматься с различными смысловыми оттенками. Поэтому, производя с такими предложениями всевозможные логические операции, нужно проявлять осторожность, стараться избегать двусмысленности.
Задание __.
У тебя должны были получиться одинаковые таблицы истинности.
Если двум высказываниям (или логическим выражениям, с помощью которых они образуются) соответствуют одинаковые таблицы истинности, то такие высказывания (выражения) называются равносильными. Равносильность обозначают с помощью обычного знака равенства.
Таким образом, ![]() .
.
Задание __.
Для доказательства формулы ![]() можно воспользоваться сравнением соответствующих таблиц истинности. Таким образом, импликация двух высказываний может быть выражена с помощью операций отрицания и дизъюнкции.
можно воспользоваться сравнением соответствующих таблиц истинности. Таким образом, импликация двух высказываний может быть выражена с помощью операций отрицания и дизъюнкции.
Можно доказать (мы не будем делать этого), что если высказывание Х образуется из нескольких высказываний ![]() то, какова бы ни была таблица истинности для высказывания Х, оно может быть выражено через
то, какова бы ни была таблица истинности для высказывания Х, оно может быть выражено через ![]() с помощью операций отрицания, конъюнкции и дизъюнкции (и, в случае необходимости, скобок, определяющих порядок применения этих операций).
с помощью операций отрицания, конъюнкции и дизъюнкции (и, в случае необходимости, скобок, определяющих порядок применения этих операций).
Задание __.
В случае одного высказывания таблица истинности содержит две строки, одна из которых соответствует значению истинности И, а другая – Л. Добавление каждого нового высказывания удваивает число строк, так как каждая имевшаяся до этого комбинация значений истинности образует две новые комбинации: со значением И и со значением Л последнего высказывания. Поэтому число строк в таблице истинности равно ![]() , где n – число исходных высказываний.
, где n – число исходных высказываний.
Задание __.
Формулы 1) и 2) представляют собой переместительный и сочетательный законы для конъюнкции, формулы 3) и 4) – распределительный закон.
Задание __.
Задача была предложена учащимся 5-6 классов на 3-ей Международной олимпиаде школ развивающего обучения.
Участники решали задачу с помощью довольно сложных логических рассуждений, причем отдельно рассматривали два случая: когда один из мальчиков правильно назвал и форму, и цвет предмета, и когда ни один из мальчиков не дал полностью правильного ответа.
Задача может быть решена и с помощью установленных нами свойств логических операций над высказываниями.
Рассмотрим следующие высказывания:
![]() : «Предмет – куб»;
: «Предмет – куб»; ![]() : «Предмет – синий»;
: «Предмет – синий»;
![]() : «Предмет – шар»;
: «Предмет – шар»; ![]() : «Предмет – зеленый»
: «Предмет – зеленый»
![]() : «Предмет - цилиндр»;
: «Предмет - цилиндр»; ![]() : «Предмет – красный».
: «Предмет – красный».
Предположим, что ни один из мальчиков не назвал неправильно и форму, и цвет предмета. Тогда дизъюнкции ![]() представляют собой истинные высказывания, а значит, и их конъюнкция
представляют собой истинные высказывания, а значит, и их конъюнкция ![]() - истинное высказывание.
- истинное высказывание.
Последнее выражение путем многократного применения распределительного закона можно преобразовать к виду
![]()
![]() (Попробуй выполнить это преобразование самостоятельно.)
(Попробуй выполнить это преобразование самостоятельно.)
Каждая из конъюнкций, заключенных, в скобки, содержит, по крайней мере, два противоречащих друг другу высказывания и, следовательно, ложна. Значит, и все выражение ложно. Таким образом, предположив, что ни один мальчик не сказал неправду дважды, мы пришли к противоречию. Значит, хотя бы один из мальчиков назвал и форму, и цвет предмета. (Вспомни, как называется такой способ доказательства.)
Конечно, рассмотренное решение задачи использует довольно громоздкое преобразование логических выражений, которое пока для тебя не очень привычно. Зато рассуждения, приводящие к решению, оказываются достаточно простыми и четкими.
Задание __.
Предикаты А (х), В (х), С (х) становятся высказываниями (истинными или ложными) при подстановке вместо х любого действительного числа.
Предикат D (х): «![]() » имеет смысл (превращается в высказывание) при любом действительном х, кроме х = 0. Запись «
» имеет смысл (превращается в высказывание) при любом действительном х, кроме х = 0. Запись «![]() » нельзя считать ни истинным, ни ложным высказыванием. Ведь числу 5 может быть равно или не равно только какое-то число, а выражение
» нельзя считать ни истинным, ни ложным высказыванием. Ведь числу 5 может быть равно или не равно только какое-то число, а выражение ![]() никаким числом не является, оно просто не имеет смысла.
никаким числом не является, оно просто не имеет смысла.
Для предиката Е (х) в самой его записи указано, что его следует рассматривать только для натуральных чисел х. (Кстати, если бы этого указания и не было, все равно имеет смысл говорить только о натуральных х, поскольку для других типов чисел понятие кратности не существует.)
Переменная в предикате G (x) может принимать любые «значения» из множества школьников.
Обобщая рассмотренные случаи, мы можем заключить, что каждый предикат рассматривается (математики говорят «определен») на некотором множестве значений переменной. Это множество может непосредственно задаваться при описании предиката или быть найдено исходя из условий, при которых предикат имеет смысл. Такое множество называется множеством (областью) определения предиката.
Понятие области определения обобщается на случай предикатов с двумя, тремя и т.д. переменными. Например, для предиката «![]() » областью определения является множество всех пар действительных чисел (х, у), за исключением таких пар, в которых у = 0.
» областью определения является множество всех пар действительных чисел (х, у), за исключением таких пар, в которых у = 0.
С каждым предикатом также связано множество тех значений переменной (или переменных), при которых предикат превращается в истинное высказывание. Для предиката А (х) – это пустое множество; для С (х) – множество всех действительных чисел; для D (x) – множество, состоящее из одного элемента – числа![]() ; для G (x) – множество всех семиклассников.
; для G (x) – множество всех семиклассников.
Множество значений переменной (переменных), при подстановке которых в предикат он превращается в истинное высказывание, называется множеством истинности этого предиката.
Множество истинности обычно обозначают буквой Т (от англ. true – истинный).
Задание __.
Соотношение между множествами X, T, F может быть выражено различными формулами, например, ![]() F; F =X/ T; F =
F; F =X/ T; F = ![]() . Предпочтительной является последняя формула, поскольку она учитывает, что Т
. Предпочтительной является последняя формула, поскольку она учитывает, что Т ![]() Х. (См. комментарии к заданиям 82, 93 раздела «Элементы теории множеств»).
Х. (См. комментарии к заданиям 82, 93 раздела «Элементы теории множеств»).
Задание __.
Поскольку при подстановке любого значения переменной из множества определения предикаты превращаются в высказывания, над ними можно совершать те же логические операции, что и над высказываниями.
Пусть А (х) – предикат с областью определения Х и множеством истинности Т. Под отрицанием этого предиката понимается предикат ![]() который при любом значении х превращается в высказывание – отрицание того высказывания, в которое при этом значении х превращается предикат А (х). Поскольку для любого высказывания существует отрицание, область определения предиката – отрицания совпадает с областью определения исходного предиката Х. Множество истинности предиката
который при любом значении х превращается в высказывание – отрицание того высказывания, в которое при этом значении х превращается предикат А (х). Поскольку для любого высказывания существует отрицание, область определения предиката – отрицания совпадает с областью определения исходного предиката Х. Множество истинности предиката ![]() совпадает с множеством
совпадает с множеством ![]() тех значений х, при которых предикат А (х) становится ложным высказыванием.
тех значений х, при которых предикат А (х) становится ложным высказыванием.
Теперь рассмотрим два предиката – А (х) с областью определения ![]() и множеством истинности
и множеством истинности ![]() и В (х) с областью определения
и В (х) с областью определения ![]() и множеством истинности
и множеством истинности ![]() . О любой логической операции над предикатами А (х) и В (х) имеет смысл говорить только при условии, что они одновременно (при одних и тех же значениях х) превращаются в высказывания. Поэтому для любого предиката, образуемого из предикатов А (х) и В (х), область определения состоит из значений х, при которых имеют смысл оба исходных предиката, т.е. является пересечением множеств
. О любой логической операции над предикатами А (х) и В (х) имеет смысл говорить только при условии, что они одновременно (при одних и тех же значениях х) превращаются в высказывания. Поэтому для любого предиката, образуемого из предикатов А (х) и В (х), область определения состоит из значений х, при которых имеют смысл оба исходных предиката, т.е. является пересечением множеств ![]() и
и ![]() .
.
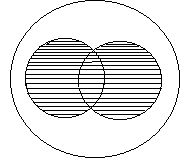
Под конъюнкцией предикатов А (х) и В (х) понимается предикат А (х)![]() В (х), который при любом значении х из множества
В (х), который при любом значении х из множества ![]() превращается в конъюнкцию высказываний, соответствующих предикатам А (х) и В (х) при этом значении х. Поскольку для истинности конъюнкции высказываний требуется истинность обоих высказываний, множество истинности конъюнкции предикатов представляет собой пересечение множеств истинности этих предикатов:
превращается в конъюнкцию высказываний, соответствующих предикатам А (х) и В (х) при этом значении х. Поскольку для истинности конъюнкции высказываний требуется истинность обоих высказываний, множество истинности конъюнкции предикатов представляет собой пересечение множеств истинности этих предикатов: ![]() На диаграмме Эйлера множество
На диаграмме Эйлера множество ![]() показано штриховкой.
показано штриховкой.
ХА ХВ
ТА ТВ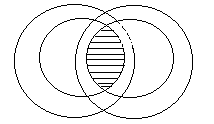
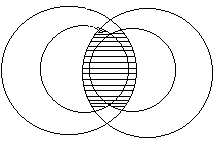
Дизъюнкцией предикатов А (х) и В (х) является предикат А (х)![]() В (х), который при любом значении х из множества ХА
В (х), который при любом значении х из множества ХА ![]() ХВ превращается в дизъюнкцию высказываний, соответствующих предикатам А (х) и В (х) при этом значении х. Определяя множество истинности предиката А (х)
ХВ превращается в дизъюнкцию высказываний, соответствующих предикатам А (х) и В (х) при этом значении х. Определяя множество истинности предиката А (х)![]() В (х), нужно учитывать одну тонкость. Если предикаты А (х) и В (х) имеют одну и ту же область определения Х , то множество истинности дизъюнкции предикатов представляет собой объединение множеств истинности этих предикатов (объясни, почему):
В (х), нужно учитывать одну тонкость. Если предикаты А (х) и В (х) имеют одну и ту же область определения Х , то множество истинности дизъюнкции предикатов представляет собой объединение множеств истинности этих предикатов (объясни, почему):![]() На диаграмме Эйлера а) это множество
На диаграмме Эйлера а) это множество ![]() показано штриховкой. В общем случае, когда области определения предикатов А (х) и В (х) различны, множество истинности предиката А (х)
показано штриховкой. В общем случае, когда области определения предикатов А (х) и В (х) различны, множество истинности предиката А (х)![]() В (х) может отличаться от ТА
В (х) может отличаться от ТА![]() ТВ. Общая формула имеет вид ТА
ТВ. Общая формула имеет вид ТА![]() В = (ТА
В = (ТА![]() ТВ)
ТВ) ![]() (ХА
(ХА![]() ХВ). (Обоснуй эту формулу, пользуясь диаграммой Эйлера б). Докажи, что формула, полученная для случая а), является частным случаем последней формулы.
ХВ). (Обоснуй эту формулу, пользуясь диаграммой Эйлера б). Докажи, что формула, полученная для случая а), является частным случаем последней формулы.
а) Х б) ХА ХВ
Задание __.
В задании знаки должны быть расставлены следующим образом: варианты 1,2, 8 – знак ; варианты 4, 6 - ; варианты 3, 5, 7, 9 – знак ; для варианта 10 не подходит ни один из рассматриваемых знаков. Если твое решение отличается от приведенного, вернись к нему после того, как прочтешь комментарии к заданию.
Ситуация, рассмотренная в задании, обобщается на утверждения любой природы.
Допустим, имеются два утверждения: У1 и У2 (это могут быть и высказывания, и предикаты).
Если из утверждения У1 логически следует утверждение У2, то этот факт представляет собой новое утверждение и обозначается следующим образом: У1 У2. Пусть, например, У1: «х – отрицательное число»; У2: «х < 5». Тогда У1У2. Словесно данный факт можно сформулировать так: «Из того, что число отрицательно, то оно меньше пяти». (Тот же факт можно было бы записать и виде У2 У1, но такая запись используется редко.)
Если бы мы попытались поменять местами утверждения У1 и У2, не изменяя связывающего их знака, то пришли бы к ошибочному утверждению У2 У1 (оно называется обратным по отношению к утверждению У1 У2): «Из того, что число меньше 5, следует, что оно отрицательно». Очевидно, что это не так, ведь существуют и неотрицательные числа, меньше 5.
Если из утверждения У1 следует утверждение У2 (У1У2), то утверждение У1 называют достаточным условием для У2, а утверждение У2 – необходимым условием для У1.
Смысл терминов «достаточное условие» и «необходимое условие» вполне соответствует их употреблению в обычной речи. Если из У1 следует У2, то а) достаточно выполнения У1, чтобы выполнилось и У2; б) если не выполнилось У2, то не выполнялось и У1 (иначе из него бы последовало бы У2), а, значит, выполнение У2 необходимо для У1.
Обратимся для примера к расписанию уроков 7»Ы» класса. Пусть У1: «Сегодня вторник», У2: «Сегодня 6 уроков» (У1 У2). У1 является необходимым условием для У1 (если сегодня не 6 уроков, то день не может быть вторником) но не является достаточным: может быть, сегодня и не вторник, а пятница.
Но очень часто встречаются и такие ситуации, для которых справедливы оба факта (и прямое и обратное утверждения): У1 У2, и У2 У1. Например, каждое из утверждений У1: «х – отрицательное число», У2: «х ּ (-5) – положительное число» может рассматриваться как следствие другого. В соответствии с правилом знаков и У1 У2 («Если х – отрицательное, то произведение х ּ (-5) – положительное, то х – отрицательное») – верные утверждения. В такой ситуации вместо громоздкой записи У1 У2 и У2 У1 используют более простую и наглядную: У1У2.
Если из утверждения У1 следует утверждение У2, а из утверждения У2 следует утверждение У1 (У1 У2), то каждое из этих утверждений является необходимым и достаточным условием для другого утверждения.
В качестве примера опять рассмотрим то же самое расписание уроков. Пусть У1:»Сегодня суббота», У2: «Сегодня 4 урока». Поскольку суббота – единственный день, когда бывает 4 урока, то из У1 следует У2, а из У2 следует У1. Каждое из утверждений У1 и У2 в этой ситуации является необходимым и достаточным условием по отношению к другому утверждению. Если справедливо одно из них, то справедливо и другое, если не выполняется одно, то не может выполняться и другое.
Наряду со словами «необходимо и достаточно» в математике часто используют эквивалентные (имеющие тот же смысл) термины «тогда и только тогда», «те и только те», «в том и только в том случае» (причем «тогда», «те», «в том» характеризуют достаточность, а слова «только тогда», «только те», «только в том» - необходимость). Например, утверждение «Для того, чтобы квадрат числа оканчивался цифрой 5, необходимо и достаточно, чтобы само число оканчивалось цифрой 5», можно сформулировать в виде следующих эквивалентных утверждений: «Квадрат числа оканчивается на 5, при возведении в квадрат дают число, оканчивающее на 5», «Квадрат числа оканчивается на 5 в том и только в том случае, когда само число оканчивается на 5».
Важно сделать одно замечание. Говоря о необходимых и достаточных условиях, мы имеем в виду именно логическую зависимость между утверждениями, а не причинно-следственную связь между явлениями, которые мы описываем с помощью этих утверждений. Например, тот факт, что день является субботой, не является следствием того, что в какой-то школе в этот день в седьмом классе 4 урока. Но, исходя из расписания уроков в этой школе, можно логически заключить, что день, когда в седьмом классе 4 урока, - суббота. Другой пример. Химик по покраснению лакмусовой бумажки определяет, что вещество, которым капнули на нее – кислота. Конечно, вещество не становится кислотой от того, что бумажка покраснела. Но из утверждения, что бумажка покраснела, следует утверждение, что вещество – кислота. (Приведи сам аналогичные примеры.)
Задание __.
Ты, конечно, понимаешь, что выражение «сумма цифр» с математической точки зрения не вполне корректно, ведь цифры складывать нельзя, а подразумевается сумма чисел, соответствующих этим цифрам. Тем не менее, это выражение стало общепринятым, поскольку позволяет в достаточно компактном виде сформулировать многие утверждения, касающиеся делимости чисел.
Подставляя в 1) и 4) «необходимо и достаточно», получаем хорошо известные тебе признаки делимости на 9 и на 3. Все признаки делимости представляют собой именно необходимые и достаточные условия делимости на то или иное число, т.е. условия, при невыполнении которых проверяемое число наверняка не делится на заданное число (необходимость), а при выполнении – наверняка делится (достаточность).
Правильная подстановка в 2) – «необходимо». Ведь любое число, делящееся на 9, делится на 3, а признак делимости числа на 3 – делимость на 3 его суммы цифр (другими словами, никакое число не может делиться на 9, если оно не делится на 3). Но делимость на 3 не является достаточным условием для делимости на 9 – существуют числа, делящиеся на 3, но не делящиеся на 9 (приведи примеры).
В 3) следует подставить «достаточно», так как любое число, делящееся на 9 (т.е. число, сумма цифр которого делится на 9), очевидно, делится и на 3. Но делимость на 9 вовсе не является необходимым условием делимости на 3 (почему? Приведи примеры).
А вот в случае 5) – «ловушка». Сумма цифр числа не имеет никакого отношения к его делимости на 5. Здесь «работает» совсем другой признак делимости (вспомни и обоснуй его).
Случаи 6), 7), 8) интересны тем, что решение зависит от того, находятся ли рассматриваемые фигуры в одной плоскости. Так, в случае 6), если прямая и окружность лежат в одной плоскости, то для наличия у них двух общих точек достаточно, чтобы прямая проходила через центр окружности. Если же допустить, что прямая, проходящая через центр окружности, не лежит в той же плоскости, что окружность («протыкает» плоскость, в которой расположена окружность), то у них нет ни одной общей точки.
Задание __.
Для утверждения 7) обратное утверждение справедливо только при условии с0.
Утверждения 8) и 9) следует сначала представить в «стандартном» виде «Если…, то…»:
8) «Если два числа – отрицательные, то и их сумма – отрицательное число»;
9) «Если число оканчивается на 2, то оно не является квадратом натурального числа». После этого сразу видно, что обратные утверждения не верны.
Задание __.
Признак делимости на 6: «На 6 делятся те и только те числа, которые делятся и на 2, и на 3». Таким образом, признак делимости на 6 сводится к двум известным признакам делимости – на 2 и на 3.
Задание __.
«Нет дыма без огня». Каким условием – необходимым или достаточным – является утверждение о наличии дыма для того, чтобы утверждать о наличии огня, если следовать этой пословице?
На поставленный вопрос будет легче ответить, если переформулировать пословицу следующим образом: «Если есть дым, значит, есть и огонь» Таким образом, «Есть дым» «Есть огонь», т.е. наличие дыма является достаточным условием для того, чтобы утверждать, что есть огонь.
Здесь нужно различать логическую связь между утверждениями и причинно-следственную связь между физическими явлениями – естественно, огонь возникает не из дыма. (См. комментарии к заданию 60.)
ВАРИАНТ ПРОВЕРОЧНОЙ РАБОТЫ ПО ТЕМЕ
«ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ И МАТЕМАТИЧЕСКОЙ ЛОГИКИ»
Выполни на выбор не менее трех заданий из группы 1 и не менее двух заданий из группы 2.
ГРУППА 1.
Задание 1.1.
На столе находятся: пустой чайник, пустая чашка, пустая коробка от конфет. Можно ли сказать, что множество предметов, находящихся на столе, пустое?
Задание 1.2.
А, В, С – конечные множества.
D = ( B C) А, Е= (А В) (А С).
В каком из множеств больше элементов: D или Е?
Варианты ответа:
а) D б) Е в) Одинаково
г) Для ответа не хватает данных.
Задание 1.3.
Какое из трех приведенных ниже множеств является подмножеством двух других? А={x -3< x< 5}, B={x -2< x < 8}, C={x -1 < x < 7}.
Варианты ответа: а) А., б) В, с) С, г) Никакое.
Задание 1.4.
Даны множества:
А= {1; 2; 3; 4; 5; 6; 7}, B= {4; 5; 6; 7; 8; 9; 10},
C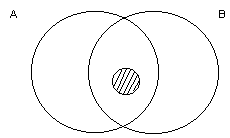 = {2; 3; 4}, D= {5; 6; 7}, E= {4; 5; 6; 7}.
= {2; 3; 4}, D= {5; 6; 7}, E= {4; 5; 6; 7}.
Какое из множеств С, D, E изображено на диаграмме Эйлера заштрихованным кружком?
Задание 1.5.
А1 - множество собак, живущих в доме № 1,
А2 – множество собак, живущих в доме № 2,
В1 – множество пород собак, живущих в доме № 1,
В2 – множество пород собак, живущих в доме № 2.
Подчеркни те из перечисленных ниже множеств, которые наверняка являются пустыми:
А1 А2, В1 В2, А1 В1, А1 В2, А2 В1, А2 В2.
Задание 1.6.
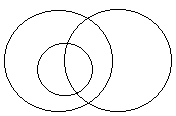
На диаграмме Эйлера кругами изображены следующие множества:
А – множество детей – участников Международной олимпиады;
В – множество всех школьников России;
С – множество мальчиков, участвующих в олимпиаде.
1)Обозначь на диаграмме каждое из перечисленных множеств соответствующей буквой;
2)Отметь на диаграмме штриховкой множество D девочек из России, участвующих в олимпиаде;
3)Запиши формулу, выражающую множество D через множества А, В, С.
ГРУППА 2.
Задание 2.1.Дано высказывание А: «Ночью все кошки серы».
Среди следующих высказываний найди ![]() :
:
а) «Днем все кошки серы»;
б) «Ночью не все кошки серы»;
в) «Ночью все кошки черны».
Определи, какое из приведенных выше высказываний имеет тот же смысл, что и высказывание «Существуют кошки, которые ночью не серы».
Задание 2.2.
Пусть D – множество всех конечных десятичных дробей.
Какое из высказываний характеризует множество D правильно и наиболее точно:
а) «D – конечное множество»,
б) «D – бесконечное множество»,
в) «D – счетное множество»?
Какое из перечисленных высказываний ложно?
Задание 2.3.
Среди следующих предложений найди предикат, истинное высказывание, ложное высказывание:
а) «Сумма любых иррациональных чисел – иррациональное число»,
б) «Существуют такие иррациональные числа, сумма которых - рациональное число»,
в) «Сумма иррациональных чисел – иррациональное число».
Задание 2.4.
Две геометрические фигуры называются равными, если их можно совместить наложением. Отсюда следует, что у двух равных треугольников углы попарно равны.
Как ты думаешь: является ли попарное равенство углов достаточным условием для равенства двух треугольников? Обоснуй свое мнение.
ЛИТЕРАТУРА
Бойка А.П. Занимательная логика: Задачи и упражнения. М.: Спсктр-5, 1994.
Брайко А.А. Краткий курс логики. – М.: Издательский центр, 1995.
Гетманова А.Д. Логика. – М.: Новая школа, 1995.
Григорьев А.П. Логика. – М., 1995.
Гоский Д.П. Логика. – М., 1963.
Кириллов В.И., Старченко А.А. Логика. – М.: Высшая школа. (Любой год издания).
Логика. Сборник упражнений. МГППК, 1998.
Логика. Учебное пособие. – Магнитогорск. МГППК, 1998.
Подшивка методической газеты для учителей информатики «Информатика» за 2003 – 2007 г.г., Издательский дом «Первое сентября»
Р.З. Ахметсафина, Е. М. Бронштейн и др. Методические указания по решению тестовых заданий. Информатика. Уфа, 2000.
Шауцукова Л.З. Информатика: Учебник для 10-11 классов. — М.: Просвещение, 2000 г.
Юркова Т.А., Ушакова Д.М. Путеводитель по компьютеру для школьника. – СПб.: Издательский Дом «Нева», 2005. – 480 с.
Яшин Б.Л. Задачи и упражнения по логике. – М.,1996.

Нравится материал? Поддержи автора!
Ещё документы из категории информатика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ