Влияние априорной неопределенности на величину пороговых сигналов и характеристики обнаружения
Влияние априорной неопределенности на величину
пороговых сигналов и характеристики обнаружения
Величина информации Кульбака – Леблера для разных моделей сигналов.
Влияние априорной неопределенности при переходе от полностью известного сигнала (2.1) к случайному сигналу с релеевским распределением огибающей (3.11) можно оценить, рассчитав объем информации Кульбака – Леблера 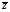 , приходящейся на один отсчет наблюдаемой выборки. Напомним, что для сигнала (2.1)
, приходящейся на один отсчет наблюдаемой выборки. Напомним, что для сигнала (2.1) 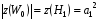 (см. ф-лу 2.5).
(см. ф-лу 2.5).
Можно показать, что для релеевского сигнала 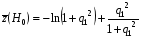 (3.15);
(3.15); 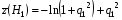 (3.16).
(3.16).
В частном случае малых отношений сигнал/шум 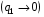 , используя известное разложение логарифма
, используя известное разложение логарифма 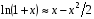 из (3.15) и (3.16) получаем
из (3.15) и (3.16) получаем 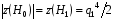 . Для сильных
. Для сильных 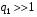 сигналов абсолютная величина средних приращений статистики при гипотезе и альтернативе различаются:
сигналов абсолютная величина средних приращений статистики при гипотезе и альтернативе различаются: 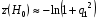 , в то время , как
, в то время , как 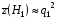 , т.е. накопление статистики при гипотезе
, т.е. накопление статистики при гипотезе 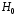 происходит существенно медленнее, чем при альтернативе
происходит существенно медленнее, чем при альтернативе 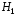 .
.
Для модели сигнала с неизвестной случайной фазой (см. 3.7) расчет информации Кульбака - Леблера возможен только численными методами.
Результаты расчета величины 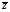 для трех указанных моделей сигнала и нескольких значений отношения сигнал/шум сведены в таблицу.
для трех указанных моделей сигнала и нескольких значений отношения сигнал/шум сведены в таблицу.
Функция правдоподобия сигнала 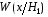
Расчёт отношения сигнал/шум 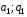
-6дБ
-3дБ
0дБ
3дБ
6дБ
12дБ
(2.1)
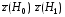
-0,25
-0,5
1
2
4
16
0,25
0,5
1
2
4
16
(3.7)
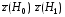
-0,024
-0,07
-0,24
1
-1,91
-10,4
0,28
0,09
0,3
1,1
2,58
14,5
(3.11)
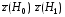
-0,023
-0,07
-0,19
-0,43
-0,8
-1,89
0,027
0,09
0,3
0,81
2,4
13,2
Из таблицы следует что, например, при отношении сигнал … шум, 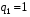 , релеевский сигнал (3.11) содержит в 3,3-5 раз меньше информации, чем полностью известный сигнал (2.1). Для случая слабых сигналов
, релеевский сигнал (3.11) содержит в 3,3-5 раз меньше информации, чем полностью известный сигнал (2.1). Для случая слабых сигналов 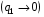 , при переходе от когерентной обработки (2.3) к некогерентной (3.11) потери информации растут пропорционально
, при переходе от когерентной обработки (2.3) к некогерентной (3.11) потери информации растут пропорционально 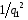 , что вполне естественно, поскольку при слабых сигналах основная информация содержится не в огибающей, а в фазе наблюдаемого процесса
, что вполне естественно, поскольку при слабых сигналах основная информация содержится не в огибающей, а в фазе наблюдаемого процесса 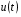 .
.
Сигнал с постоянной амплитудой и случайной фазой занимает промежуточное положение между точно известным и релеевским. Если по сравнению с дисперсией шума амплитуда сигнала мала, факт ее постоянства становится малосущественным, распределение Релея – Райса стремится к релеевскому, и характеристика оптимального детектора 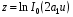 (3.10) приближается к характеристике “энергетического” приемника (3.13), соответственно
(3.10) приближается к характеристике “энергетического” приемника (3.13), соответственно 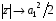 . Если же амплитуда сигнала значительно превышает дисперсию шума
. Если же амплитуда сигнала значительно превышает дисперсию шума 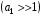 то при точно известном ее значении фаза несет мало добавочной информации, поэтому некогерентная обработка (3.10) почти не уступает когерентной обработке (2.3) соответственно
то при точно известном ее значении фаза несет мало добавочной информации, поэтому некогерентная обработка (3.10) почти не уступает когерентной обработке (2.3) соответственно 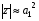 .
.
Влияние априорной неопределенности на пороговые сигналы и характеристики обнаружения.
На практике при сравнении обнаружителей для различных моделей сигналов часто пользуются не величиной информации Кульбака – Леблера, а величиной порогового сигнала, т.е. расчетного отношения сигнал..помеха в одном отсчете, обеспечивающего принятие решения с заданными вероятностями ошибок первого и второго рода  и
и 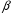 .
.
Рассмотрим пример такого расчета для полностью известного сигнала применительно к обнаружителю Неймана – Пирсона. (Напомним, что обнаружителем Неймана-Рирсона называют обнаружитель, обеспечивающий максимальное значение вероятности правильного обнаружения 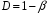 при фиксированной вероятности ложной тревоги
при фиксированной вероятности ложной тревоги  ).
).
Как было показано в разделе 2, логарифм отношения правдоподобия полностью известного сигнала имеет при гипотезе и альтернативе нормальное распределение:
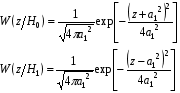 (5.1)
(5.1)
По определению, вероятность ложной тревоги есть вероятность того, что в отсутствии сигнала логарифм отношения правдоподобия превысит решающий порог:
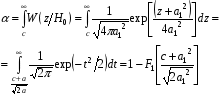
где 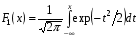 - табулированный интеграл вероятностей.
- табулированный интеграл вероятностей.
Аналогично, для вероятности пропуска
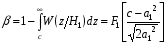 .
.
При заданных  и
и 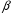 соответствующие значения аргумента
соответствующие значения аргумента 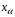 и
и 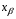 могут быть нацдены по таблицам интеграла вероятностей . В результате мы получаем систему двух уравнений с двумя неизвестными:
могут быть нацдены по таблицам интеграла вероятностей . В результате мы получаем систему двух уравнений с двумя неизвестными: 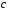 (решающий порог) и
(решающий порог) и 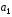 (необходимое отношение сигнал/помеха)
(необходимое отношение сигнал/помеха)
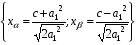 , (5.2) из которой следует:
, (5.2) из которой следует: 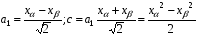 .
.
Пример расчета: задано 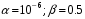 .
.
Из таблиц интеграла вероятностей находим:
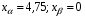 , откуда следует:
, откуда следует: 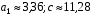 .
.
Если при том же значении  задать
задать 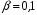 , то
, то 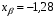 , соответственно
, соответственно 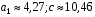 и т.д..
и т.д..
Для других моделей сигналов взаимосвязь между вероятностями ошибок, значекнием решающего порога и пороговым сигналом носит более сложный характер, поэтому расчет возможен только численными методами, напрмер, методом последовательных приближений. Существует достаточное число таблиц и номограмм, позволяющих упростить этот расчет (см., например, Справочник по радиолокации по ред. М.Сколника).
Результаты таких расчетов удобно представлять в виде характеристики обнаружения, т.е. зависимости вероятности правильного обнаружения от отношения сигнал..шум при фиксированной вероятности ложной тревоги. Примеры таких зависимостей для трех видов сигнала – с точно известными параметрами, с постоянной амплитудой и случайной фазой и с независимыми флуктуациями амплитуды приведены на рисунке 5.1.
Пользуясь характеристиками обнаружения можно определить значения порогового сигнала, которое необходимо , чтобы обеспечить заданные вероятности  и
и 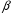 . Из графиков следует, что при переходе от полностью известного сигнала к сигналу с неизвестной фазой пороговое отношение сигнал/шум
. Из графиков следует, что при переходе от полностью известного сигнала к сигналу с неизвестной фазой пороговое отношение сигнал/шум 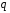 возрастает примерно на 1,5-2 дБ (соответствующие кривые сдвигаются вправо). Для сигнала с флуктуирующей амплитудой характеристика обнаружения нарастает более медленно, проигрыш а пороговом отношении сигнал/помеха по сравнению с точно известным сигналом в области
возрастает примерно на 1,5-2 дБ (соответствующие кривые сдвигаются вправо). Для сигнала с флуктуирующей амплитудой характеристика обнаружения нарастает более медленно, проигрыш а пороговом отношении сигнал/помеха по сравнению с точно известным сигналом в области 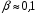 достигает 10 дБ. Обратим внимание, что в области больших значений
достигает 10 дБ. Обратим внимание, что в области больших значений 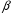 характеристика обнаружения флуктуирующего сигнала идет выше, чем для сигнала с известной амплитудой, т.е. дисперсия сигнала в этом случае повышает его наблюдаемость, однако на практике такие значения
характеристика обнаружения флуктуирующего сигнала идет выше, чем для сигнала с известной амплитудой, т.е. дисперсия сигнала в этом случае повышает его наблюдаемость, однако на практике такие значения 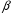 обычно не представляют большого интереса. Из графиков следует также, что при уменьшении вероятности ложной тревоги на порядок (в 10 раз), пороговый сигнал увеличивается на 0,5-1 дБ (в зависимости от типа сигнала).
обычно не представляют большого интереса. Из графиков следует также, что при уменьшении вероятности ложной тревоги на порядок (в 10 раз), пороговый сигнал увеличивается на 0,5-1 дБ (в зависимости от типа сигнала).
Обратим еще раз внимание, что приведенные на рис. 5.1. характеристики обнаружения относятся к случаю, когда необходимое пороговое отношение сигнал/помеха обеспечивается при объеме решающей выборки 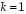 .
.
На практике это условие зачастую не выполняется и требуемое пороговое значение сигнала обеспечивается за счет накопления 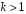 отсчетов решающей статистики, (см. ф–лы 2.3; 3.6; 3.10; 3.16). Расчет обнаружителя Неймана Пирсона при этом состоит в поиске комбинации трех переменных: решающего порога
отсчетов решающей статистики, (см. ф–лы 2.3; 3.6; 3.10; 3.16). Расчет обнаружителя Неймана Пирсона при этом состоит в поиске комбинации трех переменных: решающего порога 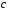 , приходящегося на один отсчет отношения сигнал/помеха
, приходящегося на один отсчет отношения сигнал/помеха 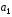 и объема выборки
и объема выборки 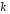 , при которых обеспечиваются заданные вероятности ошибок первого и второго рода
, при которых обеспечиваются заданные вероятности ошибок первого и второго рода  и
и 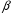 . Провести такой расчет для большинства моделей сигналов можно с использованием приведенных выше характеристик обнаружения и вспомогательных таблиц или номограмм, отражающих трансформацию распределений решающей статистики в процессе накопления.
. Провести такой расчет для большинства моделей сигналов можно с использованием приведенных выше характеристик обнаружения и вспомогательных таблиц или номограмм, отражающих трансформацию распределений решающей статистики в процессе накопления.
Наиболее прост такой расчет для полностью известного сигнала, поскольку благодаря свойству композиционной устойчивости нормального распределения решающая статистика как сумма нормально распределенных слагаемых (см. 5.1) остается нормальной, а от номера шага 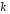 зависят только ее параметры:
зависят только ее параметры:
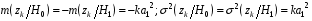
Решая относительно k систему уравнений, аналогичную (5.2):
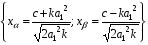 , получаем
, получаем 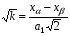
Подставляя найденное значение 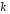 в любое из значений аргументов
в любое из значений аргументов 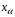 или
или 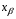 , находим порог
, находим порог 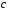 .
.
Пример расчета: пусть, как и в предыдущем примере 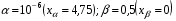 , однако отношение сигнал/помеха в одном отсчете
, однако отношение сигнал/помеха в одном отсчете 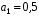 . При этом необходимый объем выборки
. При этом необходимый объем выборки 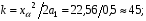 ; решающий порог
; решающий порог 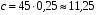 .
.
Выбор расчетных вероятностей ошибок.
Остановимся коротко гна подходах к выбору расчетных значений вероятностей ложной тревоги  и пропуска сигнала
и пропуска сигнала 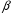 .
.
Вероятность ложной тревоги  обычно выбирается из соображений отсутствия перегрузок устройств вторичной обработки информации ложными отметками. Условие нормальной работы этих устройств обычно задается через допустимую величину частоты (темпа) ложных тревог на выходе обнаружителя, т.е. через число
обычно выбирается из соображений отсутствия перегрузок устройств вторичной обработки информации ложными отметками. Условие нормальной работы этих устройств обычно задается через допустимую величину частоты (темпа) ложных тревог на выходе обнаружителя, т.е. через число 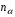 ложных тревог в единицу времени. При известном числе опытов в единицу времени (т.е. при фиксированном объеме решающей выборки) допустимая частота ложныых тревог однозначно пересчитывается в вероятность ложной тревоги в одном цикле принятия решения
ложных тревог в единицу времени. При известном числе опытов в единицу времени (т.е. при фиксированном объеме решающей выборки) допустимая частота ложныых тревог однозначно пересчитывается в вероятность ложной тревоги в одном цикле принятия решения 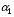 . Поясним методику такого расчета.
. Поясним методику такого расчета.
Пусть в единицу времени происходит 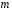 циклов принятия решения (опытов), например, просматривается
циклов принятия решения (опытов), например, просматривается 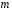 независимых элементов пространства. Вероятность отсутствия ложных тревог при проведении
независимых элементов пространства. Вероятность отсутствия ложных тревог при проведении 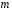 независимых опытов есть произведение вероятностей отсутствия ложных тревог в каждом из них:
независимых опытов есть произведение вероятностей отсутствия ложных тревог в каждом из них: 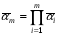 .
.
Если 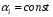 , то
, то 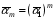 , где
, где 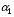 - вероятность ложной тревоги в одном опыте. Вероятность хотя бы одной ложной тревоги за время просмотра
- вероятность ложной тревоги в одном опыте. Вероятность хотя бы одной ложной тревоги за время просмотра 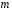 элементов
элементов 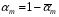 , поэтому
, поэтому
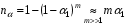 или
или 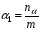 .
.
Современная обзорная РЛС зондирует за одну секунду 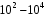 угловых элементов дальности, т.е. общее число
угловых элементов дальности, т.е. общее число 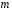 независимых элементов, просматриваемых обзорным радиолокатором за секунду обычно составляет
независимых элементов, просматриваемых обзорным радиолокатором за секунду обычно составляет 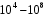 . Допустимый же темп ложных тревог
. Допустимый же темп ложных тревог 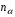 составляет порядка 1/сек, поэтому обычно задают
составляет порядка 1/сек, поэтому обычно задают 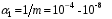 .
.
Вероятность пропуска 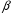 может выбираться исходя из различных соображений. Например, может быть задана вероятность обнаружения для рвзличных рубежей дальности, иногда
может выбираться исходя из различных соображений. Например, может быть задана вероятность обнаружения для рвзличных рубежей дальности, иногда 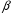 задаётся из условия устойчивого сопровождения траектории (при большой вероятности пропуска за счёт частого попадания отметок возможен срыв автосопровождения) и т.п. Типичным значениями
задаётся из условия устойчивого сопровождения траектории (при большой вероятности пропуска за счёт частого попадания отметок возможен срыв автосопровождения) и т.п. Типичным значениями 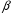 для радиолокации являются значениями
для радиолокации являются значениями 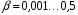 .
.
В последнее время всё чаще используется ещё один подход к выбору величины 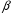 , основанный на критерии минимума среднего времени обнаружения цели, внезапно появляющейся в зоне обзора. Можно показать, что среднее время обнаружения связано с вероятностью обнаружения в одном цикле наблюдения
, основанный на критерии минимума среднего времени обнаружения цели, внезапно появляющейся в зоне обзора. Можно показать, что среднее время обнаружения связано с вероятностью обнаружения в одном цикле наблюдения 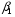 следующим соотношением:
следующим соотношением: 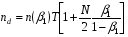 , где
, где 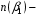 объём выборки необходимый для обеспечения в одном цикле принятия решения вероятности пропуска
объём выборки необходимый для обеспечения в одном цикле принятия решения вероятности пропуска 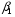 ;
; 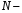 число направлений в зоне обзора;
число направлений в зоне обзора; 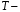 период повторения импульсов. Из формулы следует, что величина
период повторения импульсов. Из формулы следует, что величина 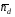 неограниченно возрастает как при
неограниченно возрастает как при 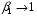 (поскольку
(поскольку 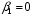 соответствует бесконечная длительность наблюдения); минимуму
соответствует бесконечная длительность наблюдения); минимуму 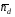 , как показывают расчёты, в большинстве случаев соответствует значение
, как показывают расчёты, в большинстве случаев соответствует значение 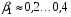 .
.

Нравится материал? Поддержи автора!
Ещё документы из категории коммуникации, связь:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ