Алгебра матриц. Системы линейных уравнений
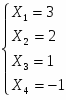
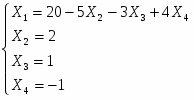
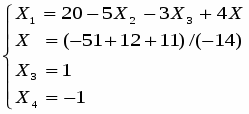
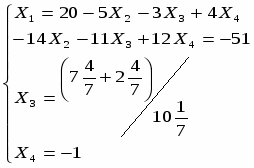
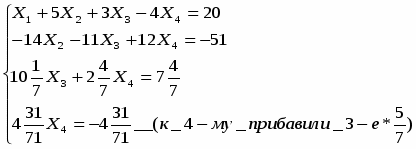
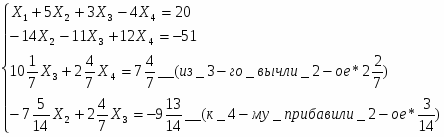

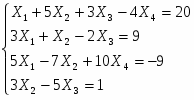
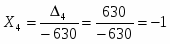
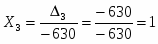
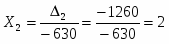
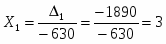
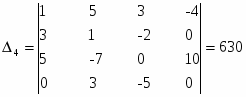

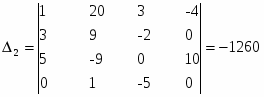
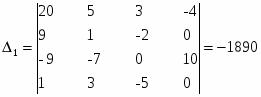
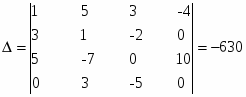
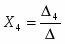
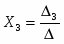
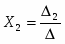
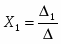
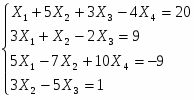
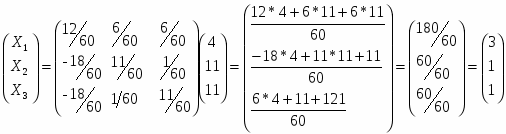
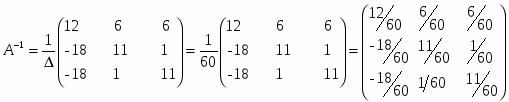
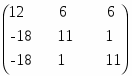
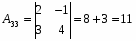
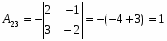
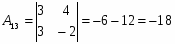
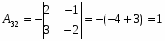
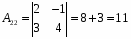
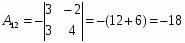
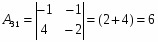
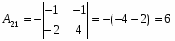
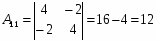
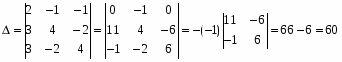
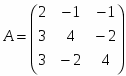
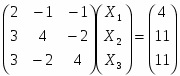
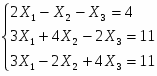
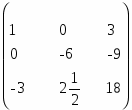
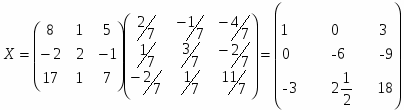
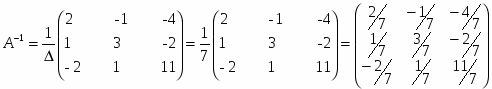
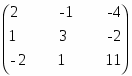
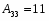
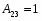
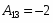
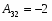
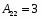
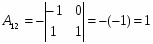
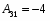
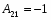
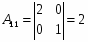
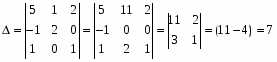
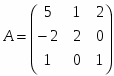
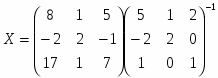
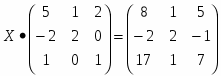

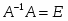
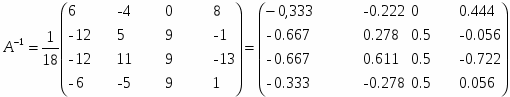
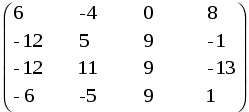
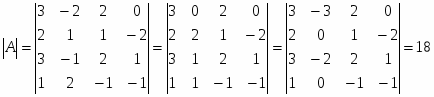
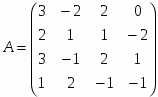
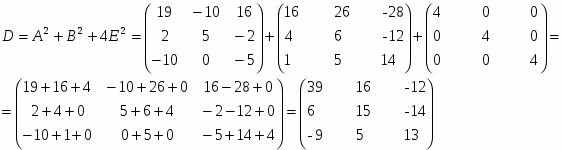
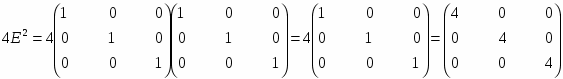
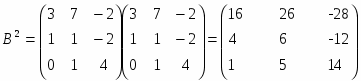
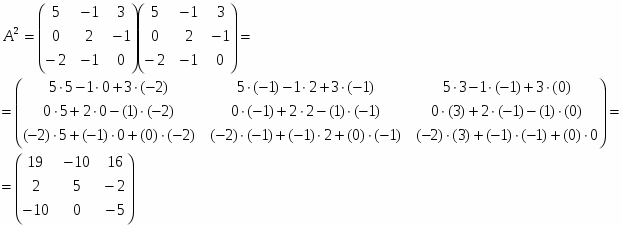
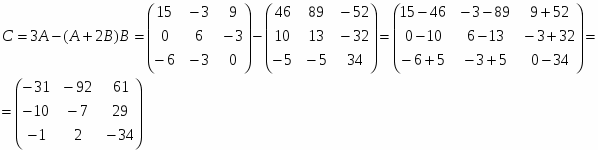
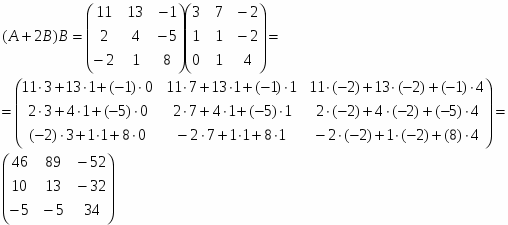
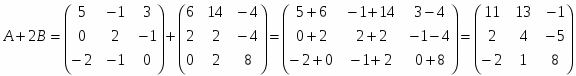

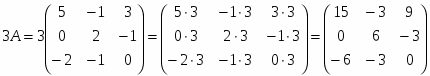
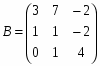
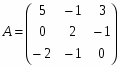 Вариант 6
Вариант 6
Тема: Алгебра матриц
Задание: Выполнить действия над матрицами.
1) С=3A-(A+2B)B
2) D=A2+B2+4E2
Тема: Обращение матриц
Обратить матрицу по определению:
Определитель матрицы:
Далее находим матрицу алгебраических дополнений (союзную матрицу):
Обратную матрицу находим:
По определению обратной матрицы:
Действительно:
Тема: решение матричных уравнений
Задание 1: Решить матричное уравнение:
Решение.
Нахождение столбца Х сводится к умножению матрицы на обратную:
Матрица коэффициентов А:
Найдем обратную матрицу A-1:
Определитель матрицы A:
Алгебраические дополнения:
Транспонированная матрица алгебраических дополнений:
Запишем выражение для обратной матрицы:
Итак, выполняем умножение матриц и находим матрицу X:
Ответ:
Задание 2: Решить систему уравнений матричным способом
Решение
Матричная запись уравнения:
Матрица коэффициентов А:
Найдем обратную матрицу A-1:
Определитель матрицы A:
Алгебраические дополнения:
Транспонированная матрица алгебраических дополнений (союзная матрица):
Запишем выражение для обратной матрицы:
Вычислим столбец неизвестных:
Тема: Решение систем линейных уравнений методом Крамера и Гаусса
Задание 1: Исследовать и решить систему по формулам Крамера:
Найти решение системы уравнений по методу Крамера.
Согласно методу Крамера, если определитель матрицы системы ненулевой, то система из 4-х уравнении имеет одно решение, при этом значение корней:
,,,,
Где:
- определитель матрицы коэффициентов – ненулевой.
- определитель матрицы полученной путем замены первого столбца матрицы коэффициентов на столбец свободных членов.
- определитель матрицы полученной заменой второго столбца матрицы коэффициентов на столбец свободных членов.
- определитель матрицы полученной заменой третьего столбца матрицы коэффициентов на столбец свободных членов.
- определитель матрицы полученной заменой четвертого столбца матрицы коэффициентов на столбец свободных членов.
Итак:
,
,
.
Задание 2: Решить эту систему по методу Гаусса.
Метод Гаусса заключается в сведении системы к треугольному виду.
Видим, что решение системы по методу Гаусса совпадает с решением по методу Крамера.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ