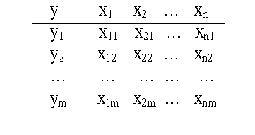ЛЕКЦИЯ №9

МНОГОЧЛЕНЫ ЧЕБЫШЕВА

1. Определение и свойства

2. Интерполяция по Чебышевским узлам

3. Многочлены равномерных приближений

4. Экономизация степенных рядов

Многочленом Чебышева n-ой степени называется функция

T_n(x)=cos (narccos) n=0,1,2 …,x[-1;1] ; (9.1)

Докажем, что при любом n=0,1,2

n=0: T₀(x)=cos0=1;

n=1: T₁(x)=cos(arccos x)=x;

n=2: T₂(x) =cos(2arccos x);

Обозначим α=arccosx

T_n(x)=cos2α ;

T_n+1(x)=cos((n+1)α) ;

T_n-1(x)=cos((n-1)α) ;

cos((n+1)α)+ cos((n-1)α)-2cos(2nα/ α)cos(2α/ α)=2 cosnα cosα;

T_n+1(x)+ T_n-1(x)=2 T₁(x) T_n(x);

T_n+1(x)= 2xT_n(x)- T_n-1(x); (9.2)

Свойства многочлена Чебышева:

1. Все функции T_n(x) являются многочленами при n=0,1,2,…

2. Степени этих многочленов возрастают с увеличением n, причем старший член T_n(x)=2^n-1x_n

3. Многочлены T_n(x) при четных n выражаются через четные функции , при нечетных n-через нечетные функции.

Проверим:

T₂(x) =2х²-1

T₃(x) =2х (2х²-1) =4х³-2х

T₄(x) = 2х (4х³-3х)-2х²+1=2³х⁴-3х²+1

4. На отрезке [-1;1] многочлен T_n(x) имеет ровно n различных действительных корней, которые рассчитываются по формуле:

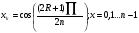
Докажем:

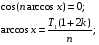
Так как arccosx[0; Π];k=0,1,…n-1,чтобы туда попадал arcos

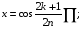
5. Корни многочлена Чебышева перемножаются, чередуются с точками их экстремума, причем максимум

T_n(x) на [-1;1] равен 1,т.е

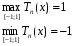
Для точек экстремума существует связь:

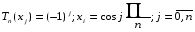
Введем нормированный многочлена Чебышева (старший коэффициент =1, перед х в максимальной степени)

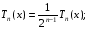(9.3)

Теорема Чебышева

Из всех многочленов степени n со старшим коэффициентом = 1, нормированный многочлен Чебышева отклоняется от нуля на отрезке [-1;1] , т.е не существует многочлена Р_n *(x), что :

max | Р_n*(x)| < max | T^_n(x)|

[-1;1] [-1;1] Доказательство не нужно.

Интерполяция по Чебышевским узлам

Задача: Пусть есть некоторая функция f(x), определенная на отрезке [a;b]. Как расположить на отрезке [a;b] n+1 узел интерполяции таким образом, чтобы минимизировать максимальное отклонение интерполяционного полинома Лагранжа от f(x), т.е ошибку аппроксимации.

Остаточный член полинома Лагранжа

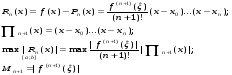
Необходимо минимизировать этот максимум, т.е необходимо найти такие узлы x_k , 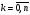которые минимизировали бы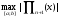

Сведем [a;b] к отрезку [-1;1]

Должна существовать связь х[a;b] с t [-1;1]

a b

t

x

-1 1

Связь: x= Ct+D

C-коэффициент сжатия (растяжения, D-параллельный перенос)

Если t=1

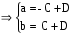
Если t=-1

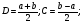
Тогда:

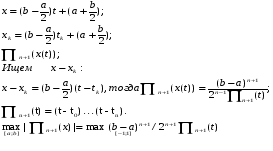(9.4)

Для того чтобы минимизировать (9.4), необходимо найти такие корни

t_k[-1;1], 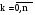, при котором Π_n+1(t) будет минимальным.

По теореме Чебышева полином Т_n+1нормирован многочленом Чебышева, наименее отклонен от нуля на [-1;1], поэтому в качестве искомых корней необходимо взять корни многочлена Чебышева на [-1;1]

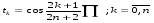(рассмотрим полином n+1-ой степени)

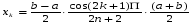
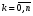(9.5)

Узлы интерполяции, определим по формуле (9.5) обеспечивают min, max ошибку аппроксимации при помощи интерполяционных полиномов.

Многочлены равномерных приближений

Если функция f(x) ∞-но дифференцируема на [a;b] и в качестве узлов интерполяции берутся корни многочленов Чебышева, приведенные к [a;b], то справедливо:

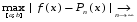
Т.е имеет место равномерная сходимость последовательности интерполяционного полинома Лагранжа функции f(x).

Теорема Вейерштрасса: для любой непрерывной функции f(x) на [a;b] найдется полином Q_n(x), что |f(x)- Р_n(x)| < ξ для любой ξ>0 , любое х[a;b].

Т.е для любой f(x) непрерывной на [a;b],может быть построена аппроксимирующий наилучший полином, который минимизирует максимальное отклонение между f(x) и Q_n(x). Такие полиномы называют многочленами наилучших равномерных приближений.

К сожалению, общий вид таких полиномов и способы построения не известны.

Экономизация степенных рядов

Ряд Тейлора представляет собой локальную аппроксимацию для f(x) степенной функции вида xⁿ можно заменить многочлен Чебышева и получить разложение по этим многочленам вместо степенного ряда:

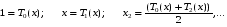
Такой процесс называется экономизацией степенного ряда.

Разложение по многочленам Чебышева имеет меньшую максимальную погрешность.

ЛЕКЦИЯ №10,11

ИНТЕРПОЛЯЦИОННЫЕ СПЛАЙНЫ

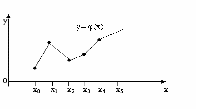
Когда интерполяционный отрезок [a;b] велик, нет, основания считать, функцию f(x) достаточно гладкой, на [a;b], то нельзя повышать точность аппроксимации за счет увеличения степени интерполяционного многочлена.

Связано это с тем, что у многочлена n-ой степени может быть n-1 точка экстремума. При n→∞ график многочлена начинает сильно колебаться

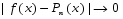
Такое явление называют феноменом Рунге.

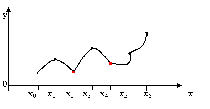
Поэтому более перспективным является применение кусочно-полиномиальной аппроксимации, при которой аппроксимирующая функция составляется из отдельных многочленов (сплайнов). Каждый из которых (одинаковы и наибольшей степени) определен на своем участке отрезка [a;b].

Рассмотрим аппроксимацию кусочно-линейной функции (линейный сплайн).

Пусть f(x) задана таблично на [a;b], т. е определены некоторые узлы интерполяции a≤x₀<x₁<…<x_n≤b

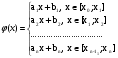кусочно-линейная функция

Необходимо: φ(x_i)=y_i=f(x_i), для приближения функции.

Определим a_i и b_i.

x=x₀: φ(x₀)=f(x₀)=y₀ a₁x₀+b₁=y₀

x=x₁: φ(x₁)=f(x₁)=y₁ a₁x₁+b₁=y₁

a₂x₁+b₂=y₁

x₀ x₁ x₂

Получим систему:

а₀x₀+b₁=y₀ (решаем по отдельности каждую систему)

a₂x₁+b₂=y₁

a₂x₁+b₂=y₁

a₂x₂+b₂=y₂ (10.2)

a_nx_n-1+b_n=y_n

a_nx_n +b_n= y_n

Таким образом, получена система из 2n уравнений для поиска 2n неизвестных. Причем, система (10.2) образована из n систем линейных уравнений для 2-х неизвестных, каждая из которых может решаться независимо от остальных.

Кусочно-линейная функция φ(x) вида (10.1) внутри интервала (х_i-1;x_i), 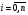непрерывна и дифференцируема, а в точках x_i, непрерывна, но не дифференцируема (в этих точках к графику функции невозможно построить касательную).

Кусочно-квадратичная аппроксимация

Пусть f(x) задана таблично на [a;b], но n=2m (четно) a≤x₀<x₁<…<x_n≤b

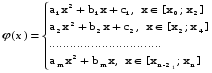
Чтобы функция приближала f(x) наложим ограничения φ(x_i)=y_i=f(x_i), .

Общее число узлов 2n+1, если n-четное.

Для нахождения неизвестных коэффициентов a_k,b_k,c_k необходимо построить 3m условий.

k=1

[x₀;x₂]

Обобщим, получим систему:

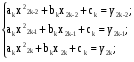
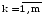(10.4)

Для нахождения неизвестных имеем 3m условий. При каждом значении 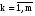можем построить систему линейных уравнений для a_k,b_k,c_k;

Решать ее можем независимо от остальных условий.

Кусочно- квадратичная φ(x) вида (10.3) внутри интервала (x_2n-2-x_2n), 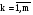является непрерывной и дифференцируемой два раза, а в точках x_2i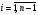

является непрерывной, но не дифференцируемой.

Определение Сплайна

Пусть на отрезке [a;b] задана некоторая система узлов a₀≤x₀< x₁<…<x_n ≤b

Сплайном S_n(x) называется функция, которая определена на [a;b], l раз непрерывна и дифференцируема на нем, при этом на каждом из отрезков

[х_к-1; х_к], к = 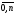, представляет собой многочлен степени m.

Разность (m-1) называется дефектом Сплайна (показывает разность между степенью составляющих его многочленов и степенью гладкости общей функции).

Если сплайн построен по некоторой таблично заданной функции f(x) таким образом, что S(х_i)= f(x_i); x_i , i= 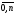- узлы интерполяции, то сплайн называют интерполяционным. Узлы сплайна и узлы интерполяции функции могут не совпадать.

Очевидно, что функция (10.1) является интерполяционным сплайном степени 1, дефекта 1, а кусочно-квадратичная функция (10.3) является интерполяционным сплайном, степени 2, дефекта 2.

Интерполяционный сплайн степени 3, дефекта 1.

Дважды непрерывно – дифференцируемый – сплайн.

Пусть задана табличная функция на [a;b], причем a= χ₀ ≤ χ₁<…< χ_n=b (узлы сплайна совпадают с узлами интерполяции). Общий вид:

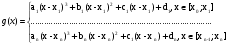
Условия:

1. g(x_i) = f(x_i)=y_i , i=

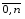
2. g(x) = c² (дважды дифференцируема) [a;b]

3. – краевые условия

Для нахождения неизвестных коэффициентов введем функцию

g_n(x) = a_k(x-x_k)³+ b_k(x-x_k)²+c₁(x-x_k)+d_k, x[ x_k-1;x_k]

1. g₁(x₀) = y₀ , g₁(x₁) = y₁ , g₂(x₂) = y₂ ,… g_n(x_n) = y_n

2. первое условие (сплайн интерполяционный)

3. 

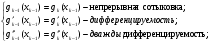
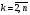
Краевые условия:

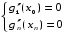
Таким образом, для нахождения 4n неизвестных мы построим 4n условий.

Теорема(10.1). Интерполяционный сплайн вида (10.5) для функции f(x) единственен.

Теорема(10.2). Пусть g(x)- интерполяционный сплайн степени 3 дефекта 1, построенный для функции f(x) С⁴ на отрезке [a;b], тогда для 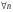найдется такая константа C>0, что:

|f(x)- g(x)|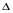⁴, 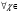[a ;b],

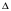= max(x_k-x_k-1), 1≤ k ≤ n

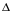- максимальное расстояние между узлами интерполяции.

Линейный фильтр

Понятие линейного сплайна позволяет сформулировать подходы к построению линейных фильтров, предназначенных для устранения случайных ошибок в данных.

Обычно в ходе измерений на процесс фиксации данных оказывают влияние случайные помехи. Для того, чтобы уменьшить влияние этих помех на качество интерполяции осуществляют пересчет значений функции в узлах интерполяции по следующей формуле:

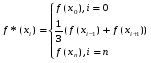
Квадратичный сплайн дефекта один

Узлы этого сплайна не совпадают с узлами интерполяции функции.

Пусть узлы интерполяции заданы на [a;b]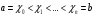

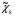- узлы сплайна, f(x_i)=y_i

χ₀ χ₁ χ₂ χ_n-1 χ_n

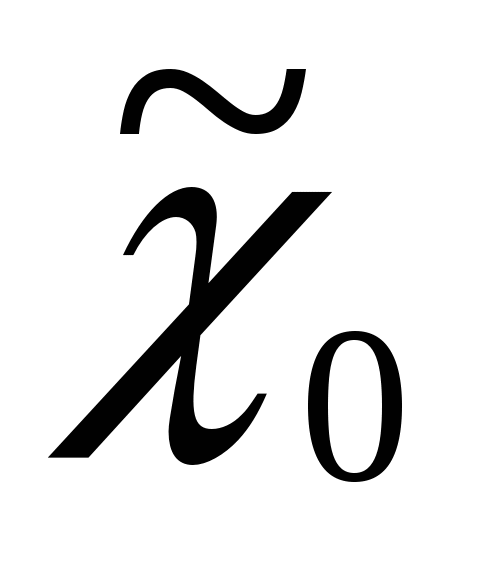
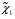
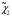
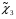
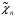
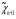
a

b

, ,

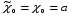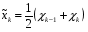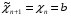
Для сплайна n+2 узлов

Квадратичный сплайн дефекта 1 имеет вид:

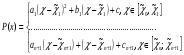
Условия:

1. 

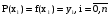
2. P(x)  C'[a;b], 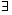первая непрерывная производная во всех точках [a;b]

3. Краевые условия:

P''(a)=A; P''(b)=B;

A и B- константы и желательно разные;

Чтобы построить сплайн необходимо найти 3n+3 неизвестных коэффициента. С этой целью сформирую функцию:

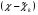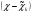P_n(x)= a_k²+b_n+c_k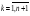

Условия:

1. P_i+1=y_i, i= 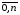- n+1 условий

2. P_k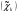= P_k+1,

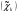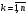
P'_k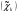=P'_k+1,

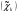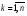
3.) P₁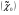=A, P''_n+1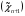-B – краевые условия;

Теорема 11.1. Квадр. Сплайн дефекта один, вида (11.1) для функции существует и единственен.

Теорема 11.2. Пусть функция f(x) дважды непрерывна и дифференцируема на [a;b], а P(x)- сплайн вида (11.1), тогда для 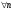, (n- связано с числом узлов интерполяции) 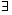такие const c₀, c₁, c₂; что для 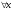из [a;b] выполняются следующие неравенства:

| f(x)-P(x) | ≤ C₀∆²

| f '(x)-P' (x)|≤C∆

| f ''(x)-P'' (x)|≤C₂

где ∆- максимальное расстояние между узлами интерполяции, т.е ∆= max(x_k-x_k-1) 1≤k≤n

Метод наименьших квадратов

1. Формула метода наименьших квадратов, для линейной функции нескольких переменных.

2. Типовые способы преобразования нелинейной функции к линейной.

3. Метод наименьших квадратов для системы линейно – независимых функций.

4. Ряды и полиномы Фурье с использованием метода наименьших квадратов.

Пусть аппроксимируемая функция представляет собой функции n переменных y= f(x₁…x_n), которая задана таблицей своих значений:

информационная матрица

Такие таблицы формируются в ходе эксперимента для реальных объектов, у которых есть одна выходная переменная (отклик), которая зависит от нескольких выходных переменных (факторов).

x_n

x₁

………………

y

необходимо аппроксимировать нашу функцию при помощи построения линейной функции (приближающей).

Необходимо построить приближение данной функции f(x₁…x_n), заданной инфо - матрицей посредством функции φ (x₁…x_n)=y, которая должна быть линейной, т.е. ее общий вид:

y= φ (x₁…x_n)=b₀+b₁x₁+…+b_nx_n (11.2)

b_i – неизвестные коэффициенты (параметры)

Задача аппроксимации состоит в определении b_i.

Каков критерий для выбора этих параметров?

Пусть f(x)-функция одной переменной и точки, в которой она определена, изображены на координатной плоскости.

x₁ x₂ x₃ x₄ x₅ x

y

y₅

y₂

y₄

y₃

y₁

(x₅;y₅)

(x₁;y₁)

(x₃;y₃)

(x₂;y₂)

(x₄;y₄)

Проводим прямую, минимизируем сумму квадратов расстояний.

Поскольку в ходе эксперимента на объект могут воздействовать случайные помехи, то в инфо – матрице могут присутствовать значения, которые не характерны для самой функции, в силу этого требовать от аппроксимирующей функции совпадения значений со значениями исходной функции во всех точках неверно.

Необходимо минимизировать сумму квадратов отклонений аппроксимирующей функции от исходных в заданных точках:

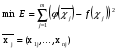(11.3)

Для данной задачи критерий (11.3) будет иметь вид:

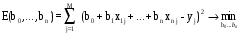(11.4)

Функция квадратичная, параболоид. Точка, в которой производные частные все будут равны 0

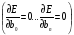(11.5)

Так как функция (11.4) является квадратичной относительно переменных b_i , то для нахождения ее минимума по этим переменным достаточно решить систему (11.5)

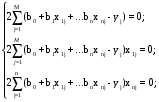(11.6)

В системе (11.6) каждое уравнение делим на 2 и раскрываем сумму; перенося сумму с частью y_j знак равенства:

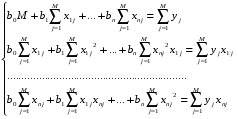(11.7)

Система (11.7) представляет собой СЛАУ относительно b_i и может быть решена одним из известных методов.

Для упрощения записи и решения представим систему (11.7) в матричном виде. Введем матрицы:

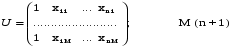
Столбец из 1 добавили в U с целью универсализации решений, так как линейную функцию можно представить в виде:

y= b₀x₀+b₁x₁+…+ b_nx_n, где x₀=1

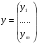
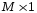
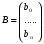(n+1)1

Тогда система (11.7) может быть записана в следующем виде:

[U^TU]B=U^TY (11.8)

Системы (11.7) и (11.8) называются нормальными. Используя, метод обратной матрицы система (11.8) имеет вид:

B= [U^TU]^-1U^TY (11.9)

(11.9) - метод наименьших квадратов для линейной функции.

17