4. Числовая окружность

Уточним, что такое числовая окружность и каковы взаимоотношения между множеством точек окружности и множеством действительных чисел.

Начало отсчета – точка A. Направление отсчета – против часовой стрелки – положительное, по часовой стрелке – отрицательное.  Масштаб – длина окружности  (рис. 4).

Вводя эти три положения, мы имеем числовую окружность. Укажем, каким образом каждому числу  поставить в соответствие точку окружности и наоборот.

Задав число  получаем точку на окружности  

 (рис. 4).

Каждому действительному числу соответствует точка на окружности. А наоборот?

Точка  соответствует числу . А если взять числа  Все эти числа своим образом на окружности имеют только одну точку 

Например,  соответствует точке B (рис. 4).

Возьмем все числа  Все они соответствуют точке B. Нет взаимно-однозначного соответствия между всеми действительными числами и точками окружности.

Если есть фиксированное число  то ему соответствует только одна точка окружности

Если есть точка окружности, то ей соответствует множество чисел

В отличии от прямой, координатная окружность не обладает взаимно-однозначным соответствием между точками и числами. Каждому числу соответствует только одна точка, но каждой точке соответствует бесчисленное множество чисел, и мы можем их записать.

5. Основные точки окружности

Рассмотрим основные точки на окружности.

Задано число  Найти, какой точке оно соответствует.

Разделив дугу  пополам, получаем точку  (рис. 5).

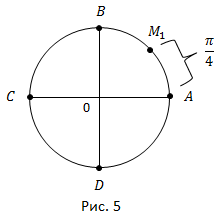
Обратная задача – дана точка  середина дуги  Найти все действительные числа, которые ей соответствуют.

Отметим на числовой окружности все дуги, кратные  (рис. 6).

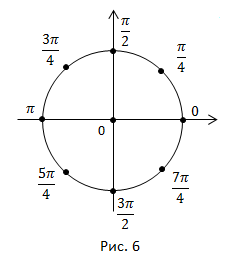
Важны также дуги, кратные 

Дано число  Нужно найти соответствующую точку.

Обратная задача – дана точка, нужно найти каким числам она соответствует.

 (рис. 7). 

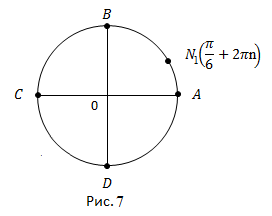
Мы рассмотрели две стандартные задачи на двух важнейших точках.

6. Задачи

Пример 1.

a) Найти на числовой окружности точку с координатой 

Решение:

Откладываем от точки Aэто два целых оборота и еще половина, и  Получаем точку M – это середина третьей четверти (рис. 8).

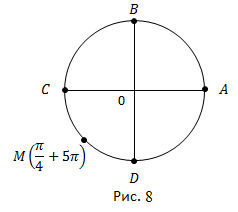
Ответ. Точка M – середина третьей четверти.

b) Найти на числовой окружности точку с координатой 

Решение:

Откладываем от точки A полный оборот и еще  получаем точку N (рис. 9).

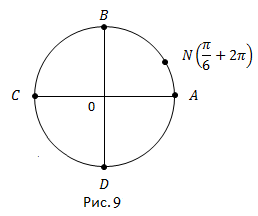
Ответ: Точка N находится в первой четверти.

7. Вывод, заключение

Мы рассмотрели числовую прямую и числовую окружность, вспомнили их особенности. Особенностью числовой прямой является взаимно-однозначное соответствие между точками этой прямой и множеством действительных чисел. Такого взаимно-однозначного соответствия нет на окружности. Каждому действительному числу на окружности соответствует единственная точка, но каждой точке числовой окружности соответствует бесчисленное множество действительных чисел.

На следующем уроке мы рассмотрим числовую окружность в координатной плоскости.