Содержание

Введение

В данной работе мы рассмотрим теорему о представлении дзета-функции Дедекинда в виде произведения L-функций и пример приложения этой теоремы к выводу функционального уравнения дзета-функции Дедекинда.

Определим некоторые понятия. Пусть k - конечное расширение поля Q, a - некоторый главный идеал поля k. Рассмотрим его разложение на простые идеалы

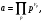где 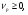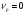для почти всех p.

Через N (a) обозначим абсолютную норму идеала a, т.е. 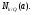Определим дзета-функцию Дедекинда :

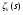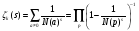
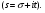
Кроме того каждому характеру сопоставим L-ряд

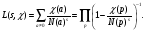
Глава 1. Теорема о представлении дзета-функции Дедекинда произведением L-рядов Дирихле

Докажем следующую теорему

Теорема. Пусть K - конечное абелево расширение поля k; тогда

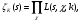
где произведение справа распространяется на все примитивные характеры, согласованные с характерами группы классов 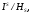где S - исключительное множество в k, 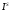- группа всех идеалов поля k, взаимно простых с S, 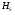- подгруппа конечного индекса, образованная теми элементами из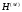, которые содержат нормы относительно k идеалов из K, взаимно простых с S, 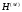- подгруппа в подгруппе главных идеалов в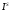, состоящая из таких главных идеалов 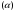, для которых 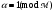и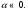

Доказательство проводится в терминах локальных множителей, причем мы рассмотрим по отдельности неразветвленный и разветвленный случаи.

1. Пусть p - неразветвленный простой идеал из k, т.е.

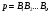
где 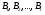- различные простые идеалы в K. Согласно теории полей классов,

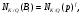где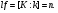

Поэтому соответствующий локальный множитель слева равен

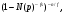
в то время как соответствующий локальный множитель справа равен

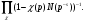
Ввиду того, что f - наименьшее положительное число такое, что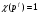 для всех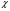, имеет место следующее легко проверяемое тождество

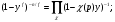
отсюда, если положить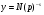, следует нужное равенство.

2. Доказательство для разветвленных простых идеалов сложнее и использует функциональные уравнения, которым удовлетворяют различные L-функции. Начнем с равенства

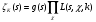
и докажем, что функция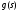тождественно равна единице. 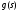равна произведению конечного числа выражений вида

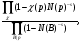
соответствующих разветвленным идеалам p.

теорема дзета функция дедекинд

Если это произведение непостоянно, оно имеет полюс или нуль в некоторой чисто мнимой точк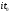е , где 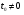. В силу функционального уравнения 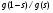представляет собой отношение гамма-функций и, следовательно, имеет только вещественные нули и полюсы. Поэтому 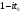, также является полюсом или нулем функции g. Мы знаем, однако, что 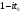не является нулем или полюсом ни для L-рядов, ни для функций 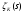. Следовательно, g постоянна, а именно равна 1.

Глава 2. Вывод функционального уравнения дзета-функции Дедекинда

Пусть k=Q, K=Q (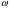), где 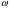- первообразный корень из 1 степени m, 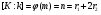. Тогда

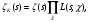(1)

где 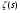- дзета-функция Римана, 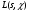- L-функция Дирихле, произведение справа распространяется на все неглавные рациональные характеры по модулю m.

Выведем функциональное уравнение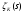

Воспользуемся функциональным уравнением для :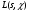

,

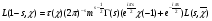где 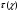сумма Гаусса. Воспользуемся (1), получим

,

,

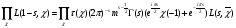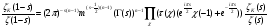используя свойство сумм Гаусса, получим

,

.

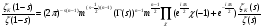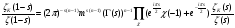Пусть для любого вещественного характера 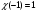, тогда

,

.

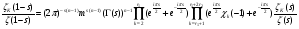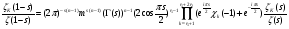Известно, что для каждого комплексного характера существует сопряжённый, тогда получим

,

,

,

.

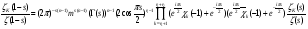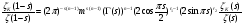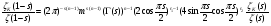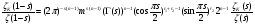Используя функциональное уравнение для дзета-функции Римана:

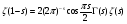
получим

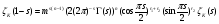
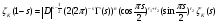
где D - дискриминант поля K.

Таким образом мы получили функциональное уравнение для дзета-функции Дедекинда в случае, когда k=Q, K=Q ().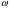

Заключение

В данной работе мы доказали теорему о представлении дзета-функции Дедекинда в виде произведения L-функций и с помощью этой теоремы вывели функциональное уравнение дзета-функции Дедекинда в случае k=Q, K=Q (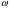), где 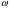- первообразный корень из 1 степени m.

Список используемой литературы

1.Касселс Дж., Фрёлих А. Алгебраическая теория чисел. - М., "Мир", 1969, с.328 - 330