Хакимзянова Нурания Идерисовна

МБОУ «Кубянская сош» Атнинского муниципального района РТ

Учитель математики и информатики

Урок по теме "Элементы комбинаторики: перестановки, сочетания и размещения"

Рано или поздно всякая правильная математическая идея находит применение

в том или ином деле.

(А.Н. Крылов) 

Цели занятия.

Образовательные:

• познакомить обучающихся с новым разделом математики: "Комбинаторика", основными понятиями и задачами, использованием в практических целях и в жизни человека;

Развивающие:

• развивать умения решать комбинаторные задачи на «перестановки», «сочетания», «размещения» по формулам, практических навыков и умений, аналитические способности, логическое мышление,

Воспитывающая:

• формировать активность личности обучающегося, умение работать в группе

• показать, что решения комбинаторных задач возникли из практических потребностей человека.

.

Оборудование: компьютеры, проектор, экран, презентация, тесты, книги.

Ход занятия

1. Организационный момент.

2. Какой смайлик
   соответствует твоему настроению на начало урока?

Класс разделен на группы. В группе может быть 4 или 5обучающихся.

Каждый обучающийся отвечает за свое поручение. (Тем самым он учится быть и руководителем, и секретарем и т.д). Переходя от каждого нового задания, обучающиеся меняются поручениями.

Проверка д/з.

Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?

ВРФ ВФР РФВ РВФ ФРВ ФВР (6)

Задачи такого типа называются комбинаторными.

Комбинаторика – раздел математики, который занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую. Слово «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять». Термин "комбинаторика" был введён знаменитым Готфридом Вильгельмом Лейбницем, - всемирно известным немецким учёным.

Комбинаторные задачи делятся на несколько групп.

3. Сообщение новых знаний.

1. Задача:

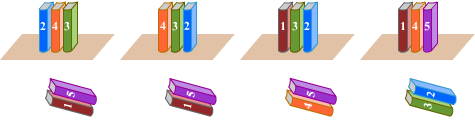
Сколькими способами можно расставить 3 различные книги на книжной полке?

abc acb

bac bca

cab cba ответ:6

Это задача на перестановки

Перестановкой из n элементов называется каждое расположение этих элементов в определённом порядке.

Pn = n(n-1)(n-2)∙…∙3∙2∙1

Pn = n!

Произведение всех последовательных натуральных чисел от 1 до n обозначается n! n! = 1 · 2 · 3 · ... · n.

Факториалы растут удивительно быстро.

n 1 2 3 4 5 6 7 8 9 10

n! 1 4 6 24 120 720 5040 40 320 362 880 3 628800

Задача. Сколькими способами можно расставить 8 участниц финального забега на восьми беговых дорожках?

P8 = 8!= 1 ∙2∙ 3 ∙4∙ 5 ∙6∙ 7 ∙8 = 40320

Задача.

Квартет

Проказница Мартышка

Осёл,

Козёл,

Да косолапый Мишка

Затеяли играть квартет

…

Стой, братцы стой! –

Кричит Мартышка, - погодите!

Как музыке идти?

Ведь вы не так сидите…

И так, и этак пересаживались – опять музыка на лад не идет.

Вот пуще прежнего пошли у них разборы

И споры,

Кому и как сидеть…

Сколькими способами можно рассадить четырех музыкантов?

P = 4! = 1 * 2 * 3 * 4 = 24

2. Задача. У нас имеется 5 книг, что у нас всего одна полка, и что на ней вмещается лишь 3 книги . Сколькими способами можно расставить на полке 3 книги?

Выбираем одну из 5-ти книг и ставим на первое место на полке. Это мы можем сделать 5-ю способами. Теперь на полке осталось два места и у нас осталось 4 книги. Вторую книгу мы можем выбрать 4-мя способами и поставить рядом с одной из 5-ти возможных первых. Таких пар может быть 5·4. Осталось 3 книги и одно место. Одну книгу из 3-ёх можно выбрать 3-мя способами и поставить рядом с одной из возможных 5·4 пар. Получится 5·4·3 разнообразных троек. Значит всего способов разместить 3 книги из 5-ти 5·4·3 = 60.

Это размещения .

Размещением из n элементов по k (k≤n) называется любое множество, состоящее из k элементов, взятых в определённом порядке из данных n элементов.

Задача. Учащиеся второго класса изучают 9 предметов. Сколькими способами можно составить расписание на один день, чтобы в нём было 4 различных предмета?

A94 = = 6∙ 7∙ 8∙ 9 = 3024

3. Задача. Сколькими способами можно расставить 3 тома на книжной полке, если выбирать их из имеющихся в наличии внешне неразличимых 5 книг?

Книги внешне неразличимы. Но они различаются, и существенно! Эти книги разные по содержанию. Возникает ситуация, когда важен состав элементов выборки, но несущественен порядок их расположения.

123 124 125 134 135 145

234 235 245

345 ответ: 10

Это сочетания .

Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данных n элементов.

Задача. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?

C₇² = = 21

Особая примета комбинаторных задач – вопрос, который можно сформулировать так, чтобы он начинался словами «Сколькими способами…»

^{Перестановки}

^{Размещения}

^{Сочетания}

^{n элементов}

^{n клеток}

^{n элементов}

^{k клеток}

^{n элементов}

^{k клеток}

^{Порядок имеет значение}

^{Порядок имеет значение}

^{Порядок не имеет значения}

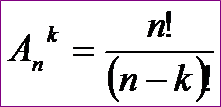
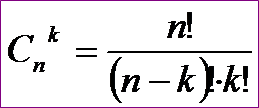
4. Физкультминутка.

5. Закрепление темы.

1. Тест по комбинаторики ( 8 обучающихся выполняют тест на компьютере, остальные на бумаге, взаимопроверка)

Вариант 1.

1. Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?

1) 30 2) 100 3) 120 4) 5

2. В 9«Б» классе 12 учащихся. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?

1) 128 2) 495 3) 36 4) 48

3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?

1) 10 2) 60 3) 20 4) 30

№ задания 1 2 3

№ ответа 3 2 4

Вариант 2.

1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?

1) 100 2) 30 3) 5 4) 120

2. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?

1) 3 2) 6 3) 2 4) 1

3. Сколькими способами из 8 учебных предметов можно составить расписание учебного дня из 4 различных уроков.

1) 10000 2) 1680 3) 32 4) 1600

№ задания 1 2 3

№ ответа 4 1 2

Вариант 3.

1. Сколькими способами можно расставить 4 различные книги на книжной полке?

1) 24 2) 4 3) 16 4) 20

2. Сколько диагоналей имеет выпуклый семиугольник?

1) 30 2) 21 3) 14 4) 7

3. В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать?

1) 22 2) 11 3) 150 4) 110

№ задания 1 2 3

№ ответа 1 2 4

Вариант 4

1. Сколькими способами могут встать в очередь в билетную кассу 5 человек?

1) 5 2) 120 3) 25 4) 100

2. Сколькими способами из 15 учеников класса можно выбрать трёх для участия в праздничном концерте?

1) 455 2) 45 3) 475 4) 18

3. В теннисном турнире участвуют 10 спортсменов. Сколькими способами теннисисты могут завоевать золото, серебро и бронзу?

1) 600 2) 100 3) 300 4)720

№ задания 1 2 3

№ ответа 2 1 4

2) Проблемный вопрос:

Может ли нам комбинаторика помочь в реальной жизни?

Решение комбинаторных задач развивает творческие способности, помогает при решении олимпиадных задач, задач из ГИА, ЕГЭ.

Области применения комбинаторики:

-учебные заведения ( составление расписаний)

-сфера общественного питания (составление меню)

-лингвистика (рассмотрение вариантов комбинаций букв)

-спортивные соревнования (расчёт количества игр между участниками)

-агротехника (размещение посевов на нескольких полях)

-география (раскраска карт)

-биология (расшифровка кода ДНК)

-химия (анализ возможных связей между химическими элементами)

-экономика (анализ вариантов купли-продажи акций) азартные игры (подсчёт частоты выигрышей)

-криптография (разработка методов шифрования)

-доставка почты (рассмотрение вариантов пересылки)

-военное дело (расположение подразделений)

Необыкновенно популярной головоломкой стал кубик Рубика, изобретенный в 1975 году преподавателем архитектуры из Будапешта Эрне Рубиком для развития пространственного воображения у студентов.

Лучшее время, показанное на чемпионате мира 1982 г. по скоростной сборке кубика Рубика, составило всего 22,95 секунды.

Кубик Рубика служит не только развлечением, но и прекрасным наглядным пособием по комбинаторике.

Вывод:

Комбинаторика повсюду.

Комбинаторика везде.

Комбинаторика вокруг нас.

VI. Д/з:

 1.В коробке находится 10 белых и 6 черных шаров.

Сколькими способами из коробки можно вынуть один шар любого цвета?

2.Ольга помнит, что телефон подруги оканчивается тремя цифрами 5, 7, 8 но забыла, в каком порядке эти цифры расположены. Укажите наибольшее число вариантов, которые ей придется перебрать, чтобы дозвониться подруге.

3. В магазине “Филателия” продается 8 разных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?

4. Проект «История комбинаторики»

VII.Итог, рефлексия.

Определи своё настроение в конце урока

Литература

1. Алгебра: учеб. для 7 класса общеобразоват. учреждений (Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева) под ред. Г.В. Дорофеева. – 2-е изд. – М. : Просвещение, 2006.

2. Евстафьева Л.П., Карп А.П. Алгебра: дидактические материалы для 7 класса общеобразовательных учреждений. М. Просвещение, 2006 (стр.65, О - 30, стр.131, П – 49).

3. Ю.Н.Макарычев, Н.Г.Миндюк Элементы статистики и теории вероятностей, Алгебра 7-9.