Урок математики в 8 классе

Тема урока: Иррациональные числа. Действительные числа.

Синиченкова Галина Алексеевна

учитель математики

МОУ Грибановская ООШ

Цели:

- ввести понятие иррационального числа, действительного числа;

- научить находить приближенные значения корней с помощью микрокалькулятора;

- познакомить с четырехзначными математическими таблицами;

- закрепить навык преобразования обыкновенной дроби в десятичную и десятичной бесконечной периодической дроби в обыкновенную;

- развивать память, мышление.

Ход урока

I Актуализация опорных знаний.

Проверка домашнего задания:

а) Представить в виде десятичной дроби: 38/11 =

б) Представить в виде обыкновенной дроби: 1,(3) = 0,3(17) =

в) Карточка:

Представить в виде обыкновенной дроби:

1 вариант 2 вариант 3 вариант

7,4(31) 1,3(4) 4,7(13)

II Устные упражнения

1) Прочитайте дроби:

0,(5); 3,(24); 15,2(57); -3,51(3)

2) Вычислите:

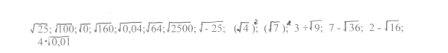
3) Округлите данные числа:

3,45; 10,59; 23,263; 0,892

А) до единиц;

Б) до десятых.

III Изучение нового материала

1. Сообщение темы и целей урока

2. Объяснение учителя

Наряду с бесконечными периодическими дробями в математике также рассматриваются бесконечные непериодические дроби. На прошлом уроке вы познакомились с понятием рациональных чисел. И знаете, что любое рациональное число можно представить в виде десятичной дроби, конечной или бесконечной.

Например, дроби

0,1010010001…

0,123456…

2,723614…

Бесконечные десятичные непериодические дроби называются иррациональными числами.

Рациональные и иррациональные числа образуют множество действительных чисел.

Арифметические действия и правила сравнения для действительных чисел определяются так, что свойства этих действий, а также свойства равенств и неравенств также как и для рациональных чисел.

Когда же получаются иррациональные числа?

1) При извлечении квадратных корней.

В курсе высшей математики доказывается, что из любого неотрицательного числа можно извлечь квадратный корень.

Например

2) Иррациональные числа получаются не только при извлечении корней.

Например

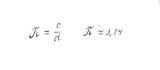
3. Устно решают №321

Какие числа называются иррациональными? (чтение ответа из учебника)

4. Сообщение «Из истории иррациональных чисел»

5. На практике для нахождения приближенных значений корней с требуемой точностью используются таблицы, микрокалькуляторы и другие вычислительные средства.

1). Знакомство с четырехзначными математическими таблицами.(стр. 35)

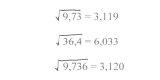
Для тех, кто интересуется более подробно познакомиться с нахождением квадратных корней с помощью таблицы может почитать пояснения к таблице.

2). В настоящее время чаще всего для нахождения приближенных значений корней пользуются микрокалькулятором.

Пример

IV Закрепление изученного материала

№322(1,3,5) Разбирают и записывают на доске.

6. Работа по карточкам

Вычислить на микрокалькуляторе с точностью до 0,001

7. Геометрически действительные числа изображаются точками числовой оси

Стр. 89 (рис.30)

V Усвоение изученного материала

Самостоятельная работа

Вариант 1

1. Сравнить числа

а) 1,(56) и 1,56

б) - 4,(45) и – 4,45

2. Записать в виде обыкновенной дроби бесконечную десятичную периодическую

дробь

а) 0,(8)

б) 4,2(43)

Вариант 2

1. Сравнить числа

а) 2,(35) и 2,35

б) - 1,(27) и – 1,272

2. Записать в виде обыкновенной дроби бесконечную десятичную периодическую

дробь

а) 1,(9)

б) 7,5(31)

VI Домашнее задание: п.21, №322(2,4,6), №323, дополнительное задание (карточки)

VII Итог урока и выставление оценок.

- Какие числа называются иррациональными?

- Какие числа образуют множество действительных чисел?