Производная

Цель: познакомить учащихся с понятием производной функции, формулами производных функций y = x² , y = x³ , y = kx+b.

1. Изучение нового материала.

• Подготовительная работа.

1. Дана функция f(x) = x²

А). Вычислить: f(5), f(-3), f(0,5)

Б). Записать в виде многочлена: f(x-3), f(x+2), f(x-a), f(x+h).

2. Дана функция S(t) = 4t+1

А). Вычислить: S(2), S(4), S(5,5)

Б). Записать в виде многочлена разность: S(t+h) – S(t).

3. Точка, двигаясь вдоль прямой, проходит за время t от начала движения путь S(t) = 3t+2. Найти S(10), S(20), S(50). Найти среднюю скорость движения на отрезках времени: [10;20], [20;50], [10;50], [t;t+h].

• Теоретическая часть.

Пусть точка движется вдоль прямой и за время t от начала движения проходит путь S(t). Рассмотрим промежуток времени от t до t+h, где h – малое число. За это время точка прошла путь S(t+h) – S(t).

Средняя скорость движения точки υ_ср =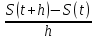

При уменьшении h это отношение приближается к некоторому числу, которое называется мгновенной скоростью υ = lim_h→0.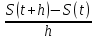

Отношение 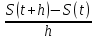можно рассматривать как приближенное значение мгновенной скорости υ(t).

Если h, уменьшаясь, стремится к нулю, то погрешность приближения становится сколь угодно малой, т.е. также стремится к нулю.

Например, если S(t) = 3t², то υ_ср = 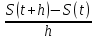= 6t + 3h.

• S(t+h) = 3(t+h)²

• S(t+h) – S(t) = 3(t+h)² – 3t² = 3(t² + 2th + h²) – 3t² = 6th + 3h².

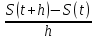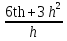• = = 6t + 3h.

Если h → 0, то 6t + 3h → 6t, т.е. υ_ср→ υ(t) = 6t.

Алгоритм нахождения мгновенной скорости:

S(t) =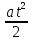

• S(t+h) =

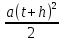
• S(t+h) – S(t) = - = = =

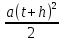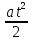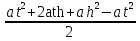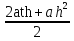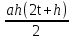
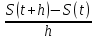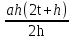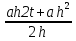• = = = at +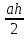

• υ(t) = lim_h→0 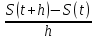= lim_h→0 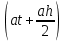= at.

Отношение 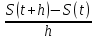называется разностным отношением, а его предел при h→ 0 называется производной функции S(t) и обозначается S'(t).

S'(t) = lim_h→0.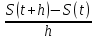

Пусть функция f(x) определена на некотором промежутке, x – точка этого промежутка и число h ≠ 0 такое, что x+h также принадлежит данному промежутку.

Тогда предел разностного отношения 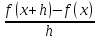при h→ 0 называется производной функции f(x) в точке x и обозначается f '(x)

f '(x) = lim_h→0.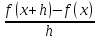

Число h, где h ≠ 0, может быть как положительное, так и отрицательное, при этом число x+h должно принадлежать промежутку, на котором определена функция f(x).

Если функция f(x) имеет производную в точке x, то эта функция называется дифференцируемой в этой точке.

Если функция f(x) имеет производную в каждой точке некоторого промежутка, то говорят, что функция имеет производную на этом промежутке.

Операция нахождения производной называется дифференцированием.

2. Практическая часть.

• Найти производную функции f(x) = 3x + 2, f(x) = 5x + 7, f(x) = kx + b

• Найти производную функции f(x) = x² , f(x) = x³, f(x) = 3x²-5x,

f(x) = -3x² + 2

3. Домашнее задание.

4. Итог урока.

Как связаны между собой средняя и мгновенная скорость движения? Что называют производной функции и как ее обозначают? Какая функция называется дифференцируемой в точке?