Школьная научно-практическая конференция

Тема:

Задачи на движение

Выполнила:

ученица 6в класса

МОУ «СОШ №42 г. Чебоксары»

Захарова Кристина Юрьевна.

Руководитель:

Белова Елена Ивановна.

Чебоксары 2009

Содержание

Введение…………………………………………………………………….3

Классификация задач на движение………………………………………..4

Противоположно направленное движение……………………………….6

Однонаправленное движение……………………………………………...9

Задачи на движение по реке……………………………………………….10

Заключение……………………………………………………………….....11

Литература…………………………………………………………………..12

Введение

Цель: ввести типы задач на движение по одной прямой, распознавать эти типы, ввести общий способ решения задач на движение вдоль прямой, разобрать арифметический способ их решения.

Умение решать задачи—показатель знаний и умений по математике. Поэтому немаловажное значение имеют задачи на движение. Решение математических задач является наиболее трудной частью для учеников при изучении математики и для меня, в частности. Задачи необходимо решать не только затем, чтобы лучше знать математику, но и чтобы эти знания можно было применять в своей дальнейшей жизни для решения разнообразных задач, возникающих в практической деятельности.

Задача—объект мыслительной деятельности, содержащий требование некоторого практического преобразования или ответа на теоретический вопрос посредством поиска условий, позволяющих раскрыть связи между известными и неизвестными ее элементами.

Задачи на движение мы начинаем изучать еще с начальных классов.

Но тогда решаем без научного подхода. Сейчас же я поставила цель их классифицировать, разбить на типы, рассматриваю принципы их решения. В учебнике Виленкина, по которому мы занимаемся, этой отдельной темы нет, поэтому эта работа представляет определенный интерес для меня и моих одноклассников.

Классификация задач на движение

С задачами на движение ученики встречаются ещё в начальных классах. В них рассматриваются 3 взаимосвязанные величины: скорость движения, т. е. расстояние, пройденное за единицу времени, время движения и пройденный путь. Скорость обозначается буквой v, время движения – t и пройденное расстояние – s.

Следует заметить, что обозначение тех или иных неизвестных обычно принятыми для них в физике буквами концентрирует внимание на существе задачи, делает более понятной для решающего задачу, исключает случайные ошибки, которые могут возникнуть из-за безликости введенных обозначений.

Допущения, которые обычно принимаются (если не оговорено противное) в условиях задач на движение, состоят в следующем:

а) движение на отдельных участках считается равномерным; при этом пройденный путь определяется по формуле s=vt;

б) повороты движущихся тел принимаются мгновенными, т. е. происходят без затрат времени; скорость при этом так же меняется мгновенно.

Рассмотрим разные типы классификаций задач на движение, наиболее часто применяемые в куре математики 5-6 классов.

• По количеству движущихся объектов.

От количества объектов, которые участвуют в движении, различают задачи на движение одного человека, одного велосипедиста, одной машины и т. д. и движение, в котором два и более участника.

• По направлению движущихся объектов.

  1. Движение навстречу друг другу или в разные стороны – противоположно направленное движение.

  2. Движение в одном направлении –однонаправленное движение.

• По времени начала движения.

  1. Одновременное движение.

  2. Разновременное движение.

• Задачи на движение по реке.

Можно приводить и задачи, в которых кто-либо выполняет какую-нибудь работу, или задачи, связанные с наполнением и опорожнением резервуаров. В задачах такого типа работа или объем резервуара играет роль расстояния, а производительности объектов, совершающих работу, аналогичны скоростям движения. Но в рамках данной работы я остановлюсь на задачах, перечисленных выше, т. к. в 5-6 классах еще не умеем решать уравнения, которые могут получиться в ходе решения таких задач. Их следует рассмотреть уже в дальнейших классах.

В задачах на движение полезно составить иллюстративный чертеж, Этот чертеж следует делать таким, чтобы на нем была видна динамика движения со всеми характерными моментами – встречами, остановками, поворотами. Хороший чертеж позволяет понять содержание задачи, не заглядывая в ее текст.

Примерный вид схем задач.

Навстречу друг другу

В одном направлении

В разных направлениях

Через сколько минут встретятся?

13,6 м/мин ? 10,4 м/мин

__________________I__________

156 м.

Через сколько минут встретятся?

13,6 м/мин 10,4 м/мин ?

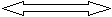_________________________I_

156 м.

Через сколько минут встретятся?

13,6 м/мин 10,4м/мин

___________________________

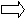
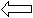
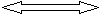156 м.

Какое расстояние будет между ними через 3 минуты?

13,6 м/мин 10,4 м/мин

? м.

___________I_________I_______

156 м.

Какое расстояние будет между ними через 3 минуты?

13,6 м/мин 10,4 м/мин

________I__________ I____

? м.

156 м.

Какое расстояние будет между ними через 3 минуты?

13,6 м/мин 10,4м/мин

I__________________________I_

156 м.

? м.

Какое расстояние будет между ними через 8 минут?

13,6 м/мин 10,4 м/мин

? м.

________________I____I________

156 м.

Какое расстояние будет между ними через 8 минут?

13,6 м/мин 10,4 м/мин

___________I__________I____

? м.

156 м.

Какое расстояние будет между ними через 8 минут?

13,6 м/мин 10,4м/мин

I__________________________I_

156 м.

? м.

Какое расстояние будет между гномами через 20 минут?

13,6 м/мин 10,4 м/мин

.

___I__________?м._____________I__

156 м.

Какое расстояние будет между гномами через 20 минут?

13,6 м/мин 10,4 м/мин

?м.

______________________I___I_

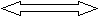
156 м.

Какое расстояние будет между гномами через 20 минут?

13,6 м/мин 10,4м/мин

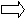
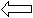
I__________________________I_

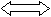156 м.

? м.

Противоположно направленное движение

Движение такого рода тоже бывает разного вида.

1. Это из одного пункта одновременно в противоположных направлениях вышли два элемента со скоростями v₁ и v₂ соответственно, то расстояние S через некоторое время t между ними находится по формуле S=(v₁+v₂)*t. В таких случаях v₁+v₂ – скорость удаления (я называю для лучшего запоминания общей скоростью).

V ₁ V ₂

S

2. Это движение навстречу друг другу, если первоначальное расстояние между двумя объектами, движущимся навстречу друг другу со скоростями v₁ и v₂, равно S, то время, через которое они встретятся, равно t=S:(v₁+v₂), где v₁+v₂—скорость сближения (я называю также общей скоростью).

V ₁ V ₂

S

Задача 1. Из одного пункта одновременно в противоположных направлениях вышли два пешехода. Скорость одного из них 5 км/ч, другого—6 км/ч. Какое расстояние между ними будет через 3 часа?

Решение. Найдем расстояние, которое пройдет за 3 часа каждый из пешеходов. Первый пешеход пройдет 5∙3=15(км), второй пешеход пройдет 6∙3=18(км). Расстояние между ними будет 15+18=33(км). Эту задачу можно решить другим способом. Каждый час расстояние между пешеходами увеличивается на 5+6=11(км), т. е. скорость удаления пешеходов равна 11 км/ч. Поэтому расстояние между ними 11∙3=33(км).

Ответ. 33 км.

Задача 2. Из двух городов А и В в 5 часов утра вышли друг другу навстречу два поезда. Первый поезд шел со скоростью 51 км/ч, второй со скоростью 57 км/ч. Через один час езды они находились друг от друга на расстоянии 432 км. В котором часу они встретятся?

Решение.

1)51+57=108(км/ч)—скорость сближения.

2)432:108=4(ч)—время преодоления 432 км.

3)5+1+4=10(ч)—время встречи.

Ответ. В 10 часов они встретятся.

Задача 3. Две электрички двигались от двух платформ навстречу друг другу. Через 3 минуты после встречи расстояние между ними стало равным 7км 500 м. Сколько метров в минуту проезжала первая электричка, если вторая проезжала 1200 м в минуту?

Задача 4. Два охотника вышли навстречу друг другу из леса с двух сторон поляны и оказались на расстоянии 450 м друг от друга. Один шел со скоростью 70 м/мин, другой—со скоростью 80 м/мин. Собака одного из них побежала навстречу другому. Добежав до него, она вернулась к хозяину и, повернув, снова бросилась к его другу. Так она продолжала свой бег до встречи двух охотников. Найти расстояние, которое пробежала собака, если ее скорость равна 12 км/ч.

Задачи на движение можно решать с помощью уравнения, зная основные правила этих задач.

Задача 5. Из поселка одновременно отправились в противоположных направлениях велосипедист и мотоциклист. Через 2 часа расстояние между ними было 104 км. Определите скорость мотоциклиста, если она была в 3 раза больше скорости велосипедиста.

Решение. 1. Меньшую скорость—скорость велосипедиста—обозначим буквой х км/ч, тогда скорость мотоциклиста будет 3х км/ч.

2. Определим скорость удаления:

(х+3х)(км/ч).

3. Определим расстояние, пройденное скоростями за 2 часа:

(х+3х)∙2(км).

4. Составим и решим уравнение: (х+3х)∙2=104

4х∙2=104

8х=104

х=13(км/ч)

5. Найдем скорость мотоциклиста: 13∙3=39(км/ч)

Ответ. 13 км/ч и 39 км/ч.

Задача 6. От двух станций, расстояние между которыми 640 км, отошли одновременно навстречу друг другу два поезда. Скорость первого поезда 68 км/ч, скорость второго—на 8 км/ч меньше. Сколько километров прошел до встречи поезд с меньшей скоростью?

Задача 7. Два автомобиля вышли из одного города в противоположных направлениях. Скорость одного из них 66 км/ч, а другого—на 8 км/ч больше скорости другого. Каково будет расстояние между автомобилями через 4 часа после их выхода?

Задача 8. С одной станции одновременно в противоположных направлениях вышли два поезда. Скорость одного из них 62км/ч, а другого—на 8 км/ч больше. Через сколько часов расстояние между ними будет 1584 км?

Однонаправленное движение

Рассмотрим движение объектов в одном направлении. Если первоначальное расстояние между точками, из которых одна догоняет другую, равно S, то время, через которое вторая точка со скоростью v₂ догонит первую со скоростью v₁ равно t=S:(v₂-v₁), где v₂> v₁.

V ₂ V ₁

S

Здесь v₂-v₁ —скорость сближения ( я в таких случаях для лучшего запоминания называю «разница скоростей»).

В случае, если v₂-v₁, расстояние между ними увеличивается со скоростью v₂-v₁—со скоростью удаления.

Задача 9. Один пешеход идет со скоростью 5 км/ч, а другой вслед за ним со скоростью 7 км/ч. В начальный момент времени расстояние между ними равно 4 км. Через какое время второй пешеход догонит первого?

Решение. Скорость второго больше скорости первого на 7-5=2 (км/ч), т. е. их скорость сближения равна 2 км/ч. Тогда время, через которое он догонит первого пешехода, равно 8:2=4 (ч).

Ответ. 4 часа.

Задача 10. Из двух пунктов одновременно в одном направлении выехали автобус и легковая машина. Автобус едет со скоростью 70 км/ч, автомашина—со скоростью 85 км/ч. Через сколько часов автомашина догонит автобус, если расстояние между пунктами 45 км?

Задача 11. Со станции А в направлении станции В вышел поезд со скоростью 72 км/ч. Одновременно со станции В в том же направлении вышел другой поезд со скоростью 60 км/ч. Через сколько часов первый поезд догонит второй поезд, если расстояние между А и В равно 60 км?

Задача 12. Из двух городов, расстояние между которыми 168 км, одновременно и в одном направлении выехали грузовая и легковая автомашины. Скорость грузовой автомашины 40 км/ч. Вычислите скорость легковой автомашины, если она догнала грузовую через 6 часов.

Задача 13. Автобус и автомашина выехали из одного и того же пункта в одном направлении. Скорость автобуса 53 км/ч, скорость автомашины 41 км/ч. Через сколько часов автобус будет впереди автомашины на 48 км?

Задачи на движение по реке

В задачах на движение по реке есть своя особенность: приходится различать скорость движения по течению и скорость движения против течения.

Если тело движется по течению реки, то его скорость слагается из скорости в стоячей воде v и скорости течения реки u:

ω=v+u,

а если против течения реки, то его скорость равна:

ω=v-u.

Скорость в стоячей воде называется собственной скоростью.

Если в условии задачи речь идет о движении плотов, то этим хотят сказать, что тело движется со скоростью течения реки.

Задача 14. Катер проплыл 72 км между пристанями по течению реки за 2 часа, а против течения—за 3 часа. За сколько часов это расстояние проплывут плоты?

Решение. Найдем скорость катера по течению реки: 72:2=36 (км/ч). А скорость катера против течения реки получится72:3=24 (км/ч). Скорость течения реки получится (36-24):=6 (км/ч). Это и есть скорость движения плотов.

Ответ. 6 км/ч.

Собственная скорость является средним арифметическим между скоростями по течению и против течения.

Задача 15. Собственная скорость катера 24 км/ч, а скорость течения реки составляет 0,15 собственной скорости катера. Определите скорость катера по течению реки.

Решение. Найдем скорость течения реки:24∙0,15=3,6 (км/ч). Скорость катера по течению будет: 24+3,6=27,6 (км/ч).

Ответ.27,6 км/ч.

Задача 16. Скорость теплохода против течения реки 36 км/ч, а скорость течения реки составляет 0,12 скорости против течения реки. Определите собственную скорость теплохода.

Задача 17. Катер шел 3 часа вниз по реке со скоростью 16 км/ч. Обратный путь он прошел со скоростью 12 км/ч. Сколько времени затратил катер на обратный путь?

Задача 18.Теплоход прошел в 0,75 часа по течению реки 16,62 км, а против течения в 0,8 часа 14,4 км. Какова скорость теплохода в стоячей воде, скорость течения реки, скорость теплохода по течению и против течения?

Задача 19. Моторная лодка прошла 48.9 км по течению реки за 3часа. Скорость течения реки 1,3 км/ч. Сколько километров пройдет лодка против течения за 4ч?

Собственная скорость является средним арифметическим между скоростями по течению и против течения.

Задача 15. Собственная скорость катера 24 км/ч, а скорость течения реки составляет 0,15 собственной скорости катера. Определите скорость катера по течению реки.

Решение. Найдем скорость течения реки:24∙0,15=3,6 (км/ч). Скорость катера по течению будет: 24+3,6=27,6 (км/ч).

Ответ.27,6 км/ч.

Задача 16. Скорость теплохода против течения реки 36 км/ч, а скорость течения реки составляет 0,12 скорости против течения реки. Определите собственную скорость теплохода.

Задача 17. Катер шел 3 часа вниз по реке со скоростью 16 км/ч. Обратный путь он прошел со скоростью 12 км/ч. Сколько времени затратил катер на обратный путь?

Задача 18.Теплоход прошел в 0,75 часа по течению реки 16,62 км, а против течения в 0,8 часа 14,4 км. Какова скорость теплохода в стоячей воде, скорость течения реки, скорость теплохода по течению и против течения?

Задача 19. Моторная лодка прошла 48.9 км по течению реки за 3часа. Скорость течения реки 1,3 км/ч. Сколько километров пройдет лодка против течения за 4ч?

Заключение

Благодаря данной работе, я научилась лучше решать задачи на движение. В учебнике математики 5-6 классов теории по данной теме нет, поэтому я захотела рассмотреть методы решения таких задач. Сейчас у меня уже нет психологического страха перед такими задачами. Я знаю приемы и действия, которые нужно применять при решении задач на движение.

Ученик, который усвоит необходимый алгоритм решения задач, может воспользоваться полученными знаниями при решении других сложных задач. Ему уже не нужно затрачивать время для нахождения ответов частичных проблем, мыслительная деятельность будет направлена на решение других важных проблем.

Литература

Буланова Л.М., Дудницын Ю.П. и др., Проверочные задания по математике, «Просвещение»

Виленкин Н.Я., Жохов В.И. и др., Математика, учебник для 5 кл., «Мнемозина», 2007

Виленкин Н.Я., Жохов В.И. и др., Математика, учебник для 6 кл., «Мнемозина», 2007

Дорофеев Г.В., Шарыгин И.Ф. и др., Математика, 5 кл., «Просвещение», 2006

Дорофеев Г.В., Шарыгин И.Ф. и др., Математика, 6 кл., «Просвещение», 2006

Лурье М.И., Александров Б. И., Задачи на составление уравнений, «Наука», 1990

Совайленко В.К., Лебедева О.В., Сборник развивающих задач с решениями для учащихся 5-6 классов, «Легион», 2005

Шклярова Т.Ф., Сборник упражнений по математике, «Грамотей», 2008