БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ВОЛОГОДСКОЙ ОБЛАСТИ

«Череповецкий лесомеханический техникум им.В.П.Чкалова»

Конспект урока по математике.

Тема: « Исследование функций с помощью производной. Построение графиков»

(практическая работа)

Разработчик

Преподаватель математики

Захарова Светлана Витальевна

г. Череповец

2014 г.

Исследование функций с помощью производной. Построение графиков.

ЦЕЛИ И ЗАДАЧИ:

Обучающие:

• Обеспечить в ходе занятия педагогические условия для формирования умения с помощью производной исследовать функцию и строить ее график,

• Повторить схему исследования функции, ее свойства,

• Повторить физический и геометрический смысл производной,

• Повторить таблицу производных, правила дифференцирования.

Развивающие:

• Формирование умения пользоваться математическими инструментами,

• Формирование умения применять свои знания при построении графиков.

Воспитательные:

• Воспитание устойчивого интереса к математике,

• Воспитание математической культуры,

• Развитие самоорганизации учащихся,

• Эстетическое воспитание.

Тип урока. Урок формирования умений и навыков.

Время занятия 1час 30 минут (пара)

Ход урока:

• Организационный момент,

• Постановка целей занятия,

• Актуализация опорных знаний,

  1. Устный опрос,

  2. Тест,

  3. Проверка теста,

  4. Образец выполнения.

• Выполнение практической работы,

• Запись домашнего задания,

• Повторение,

• Итог урока.

Организационный момент.

Приветствие учащихся. Отметка отсутствующих и опоздавших.

Постановка целей занятия.

Сегодня на уроке мы должны:

1. Повторить основные свойства функции, схему исследования функции,

2. Выполнить практическую работу самостоятельно, предварительно разобрав пример у доски,

3. Ответить на вопросы практической работы,

4. Повторение правил дифференцирования, таблицы производных, физического и геометрического смысла производной.

Актуализация опорных знаний.

1. Проверка домашнего задания: повторение основных определений и понятий: (область определения и множество значений функции; четность нечетность функции; определение возрастающей и убывающей функции, экстремумов; теоремы о возрастании и убывании функции, условие точек максимума и минимума).

2. Тест

Приложение 1. (перейти по ссылке ctrl+щелчок мышью по надписи)

3. Проверка заданий теста (СМ. ПРЕЗЕНТАЦИЮ «Проверка теста»)

(С помощью мыши выберите вариант, а затем ответ на поставленный вопрос, если он правильный выйдет надпись ВЕРНО, в противном случае выйдет надпись НЕВЕРНО, щелкните мышкой на появившейся надписи и вы вернетесь к вопросу, либо перейдете на следующий)

4. Схема исследования. (СМ. ПРЕЗЕНТАЦИЮ «Схеме исследования»)

5. Образец выполнения. Исследуйте функцию по первой производной, постройте ее график. .

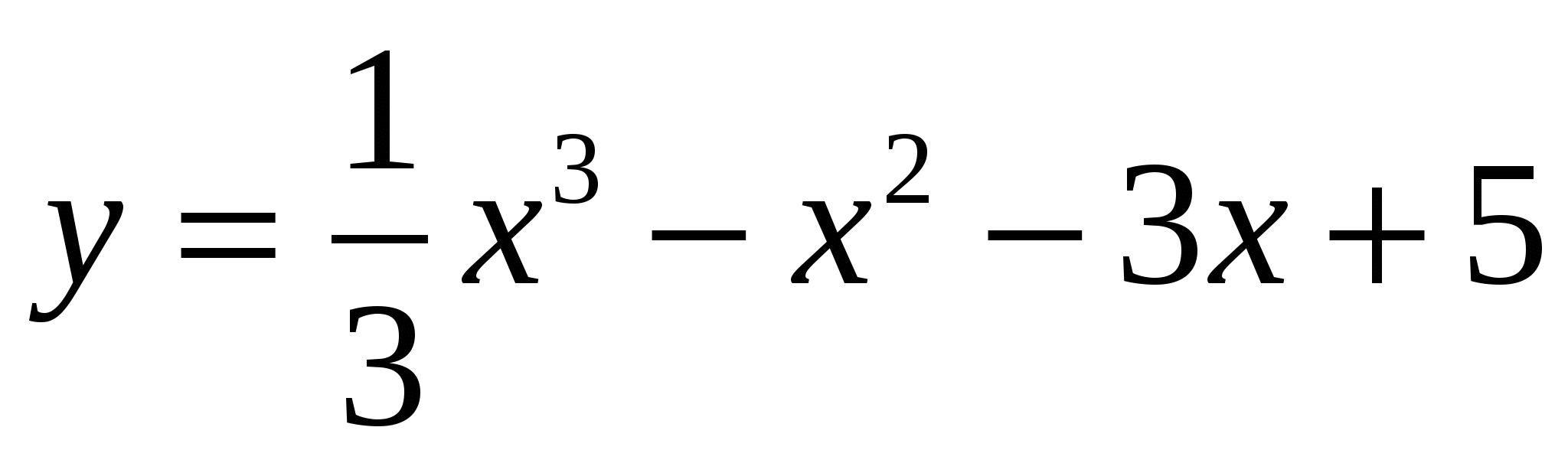РЕШЕНИЕ. Для решения поставленной задачи воспользуемся упрощенной схемой исследования.

• Точка пересечения с осью у, подставим в функцию х=0, имеем 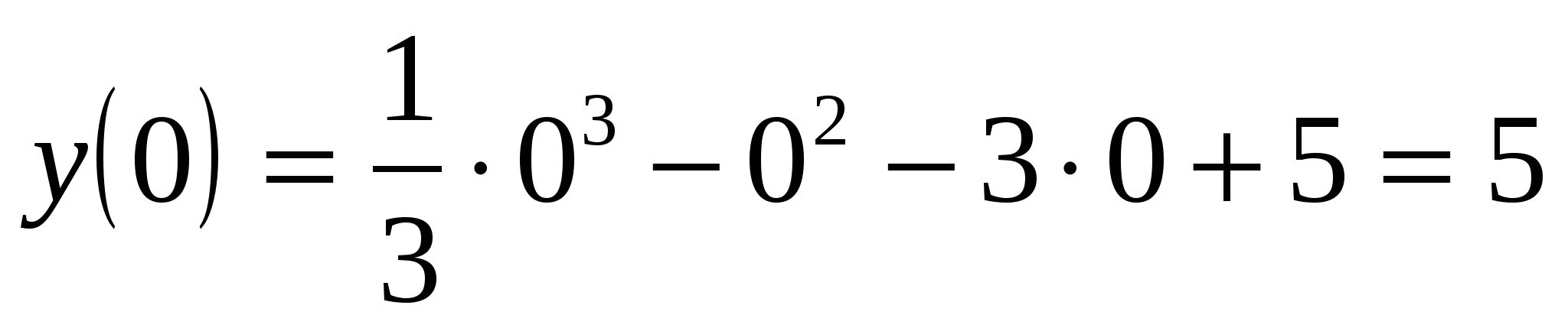(0,5)

• Найдем производную функции ,

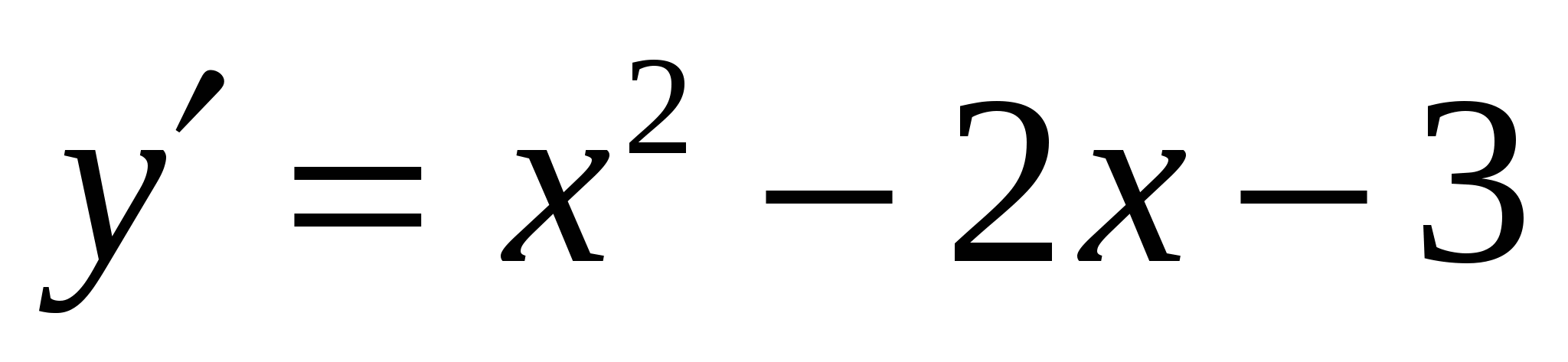• Приравняем производную к нулю, и решим полученное уравнение, 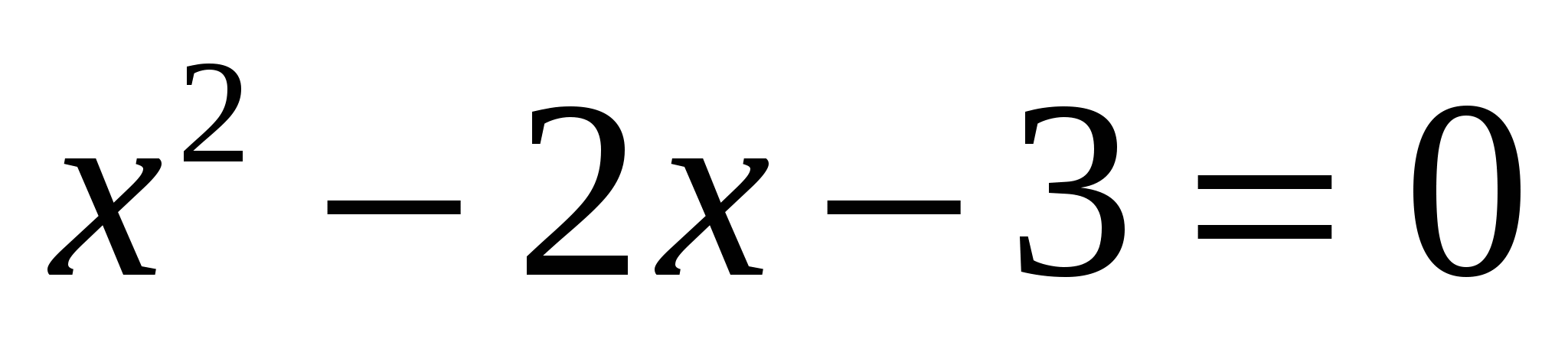, х =3, х = -1.

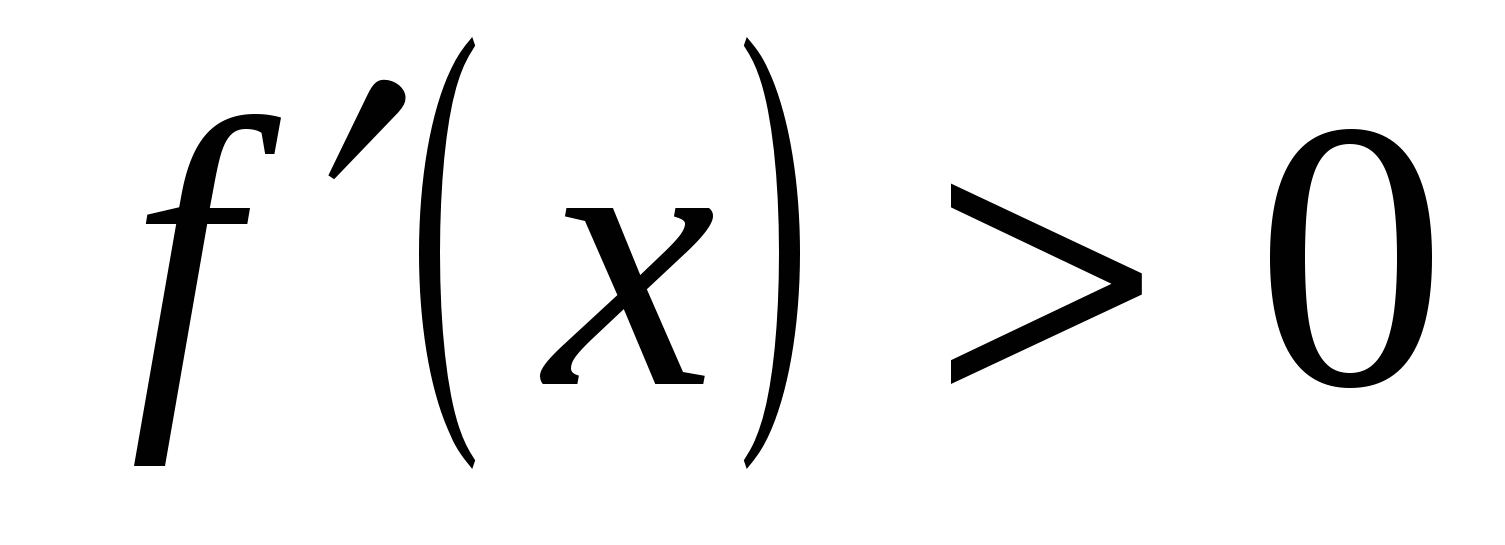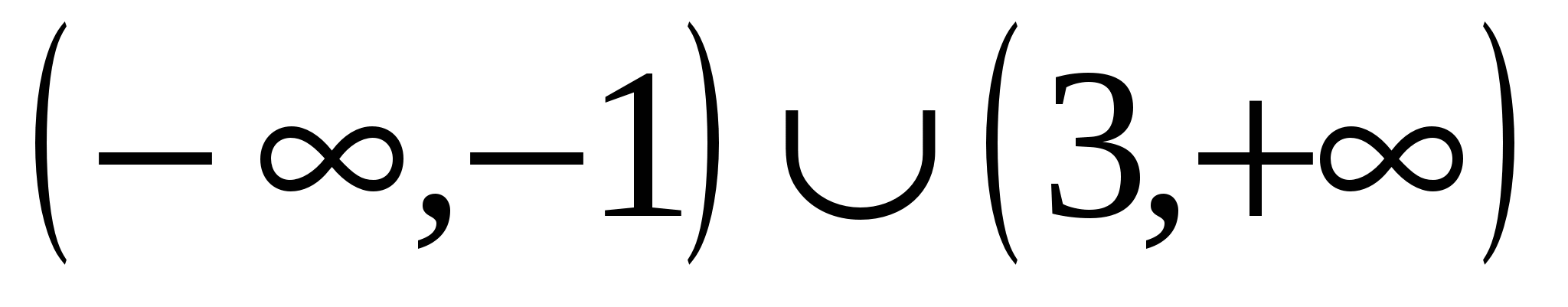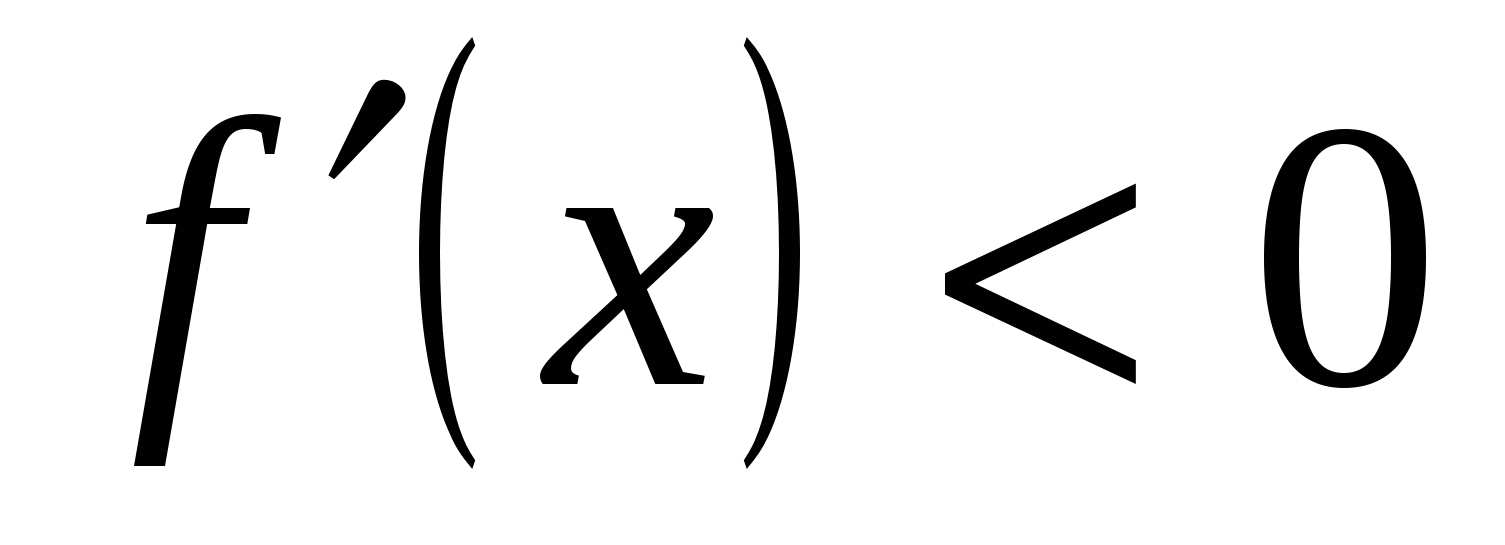• Найдем промежутки, на которых производная больше и меньше нуля, на , на .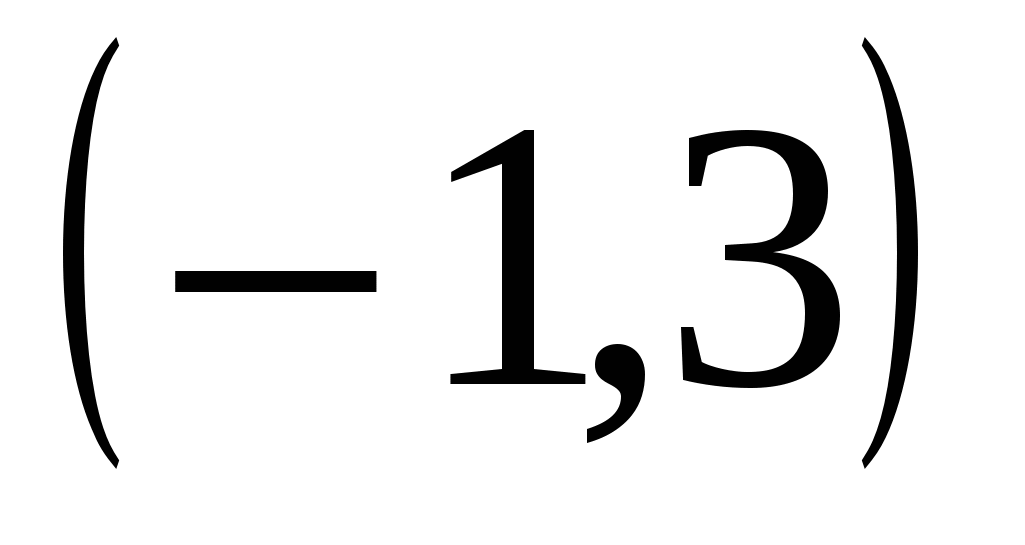

• Оформим дальше решение задачи в виде таблицы:

Х

-1

3

+

0

-

0

+

Max Min

• Найдем дополнительные точки

Х = -4,

Х=-3, у = -4,

Х=1, ,

Х=2, ,

Х=4,

Х=5 ,

Х=6 .

ГРАФИК.

Выполнение практической работы.

Работа выполняется по вариантам. Учащимся необходимо самостоятельно исследовать функцию и построить ее график. Приложение 2.

1 вариант.

2 вариант.

Проверка (СМ. ПРЕЗЕНТАЦИЮ «Проверка пр.раб»).

Повторение.

Вам сейчас будет предложено следующее задание: даны функции, каждой из которых соответствует имя героя из некоторого произведения, если вы правильно найдете производные указанных функций, то сможете каждому герою подобрать героиню. Затем, вычислив значение производной в точке х=0, сможете определить из какого произведения эти герои.

Герой

Имя героя

Функция

Герман

Евгений

Гирей

Алеко

Дон Гуан

Ибрагим

Героиня

Имя героини

Производная

Татьяна

Зарема

Дона Анна

Земфира

Маша Миронова

Лизавета Ивановна

Наташа

Параша

Произведения.

Название произведения

Ответ

Бахчисарайский фонтан

-2

Цыганы

18

Медный всадник

1

Арап Петра Великого

4

Пиковая дама

9

Каменный гость

7

Евгений Онегин

0

Капитанская дочка

3

Задание 2. Таблицу производных и правила дифференцирования мы повторили в предыдущем задании. Теперь повторим физический и геометрический смысл производной.

1. В чем заключается физический смысл производной. В частности чему равна производная пути, производная скорости, вторая производная от пути?

2. В чем заключается геометрический смысл производной, чему равен тангенс угла наклона касательной, проведенной к графику функции в точке х₀. Когда касательная параллельна оси х?

3. Вам предлагается следующее задание: Нужно разгадать зашифрованное слово. Решив задачи, и сопоставив ответ с соответствующей ему буквой, вы сможете отгадать зашифрованное слово.

Задачи.

1. Вычислите тангенс угла наклона касательной, проведенной к графику функции 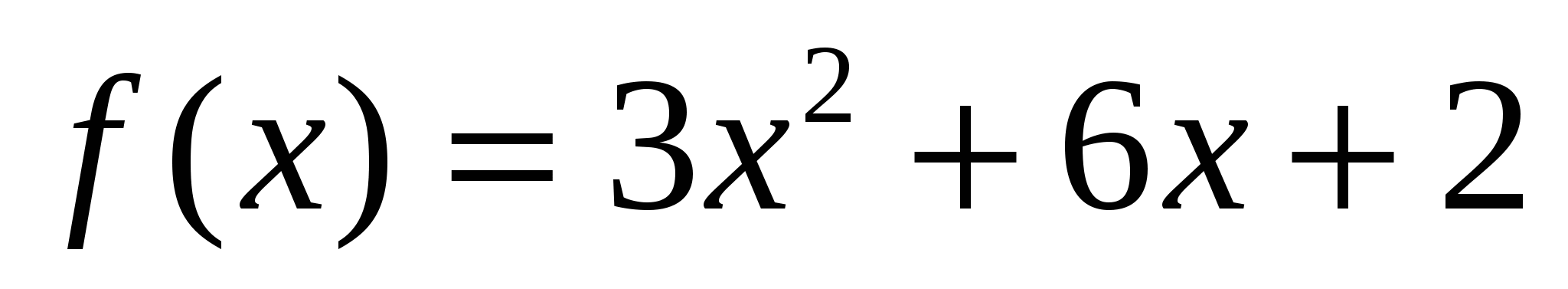, в точке х₀= - 0,5.

2. Найдите точку, в которой касательная, проведенная к графику функции 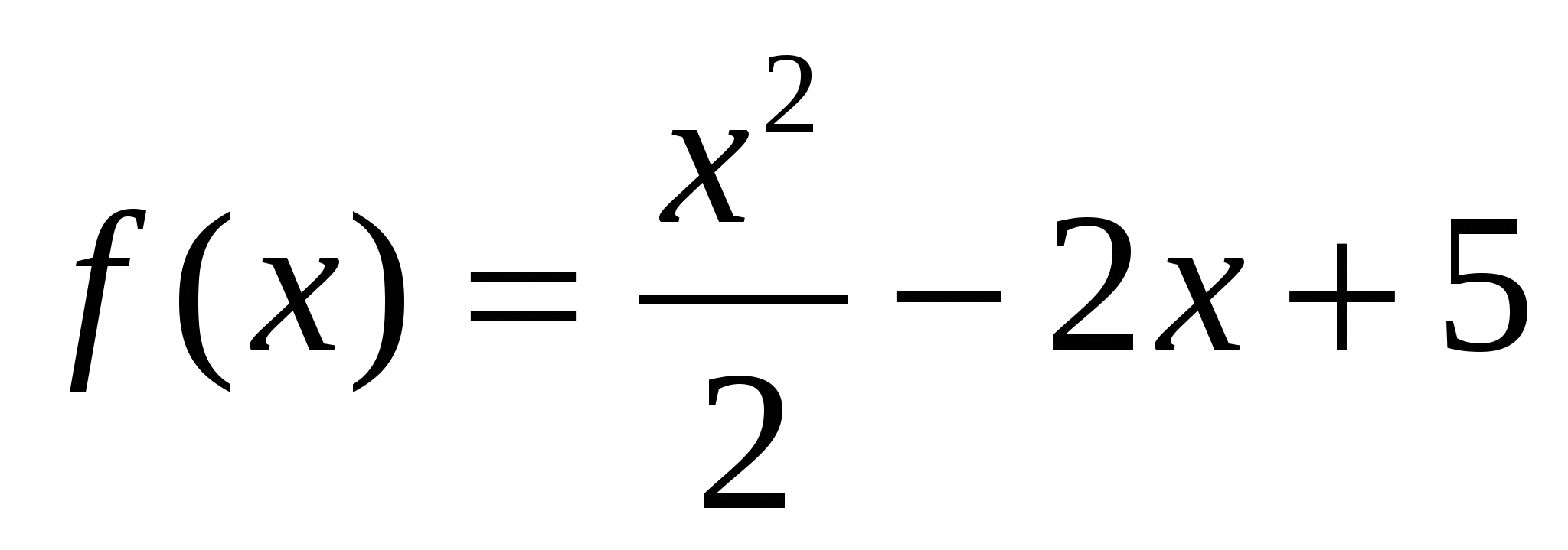, параллельна оси Х.

3. Тело движется по закону: , определите его скорость в момент времени t=1сек.

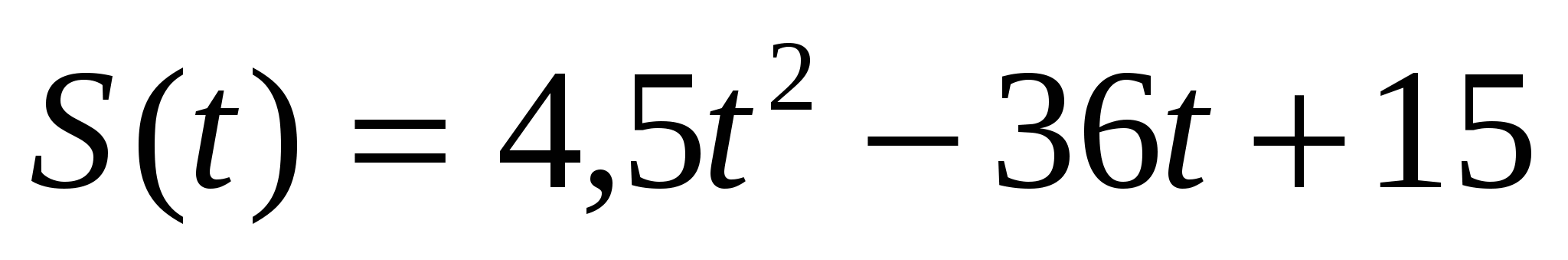4. Тело движется по закону: . Найдите момент времени, когда тело остановится.

5. Скорость материальной точки выражается формулой: 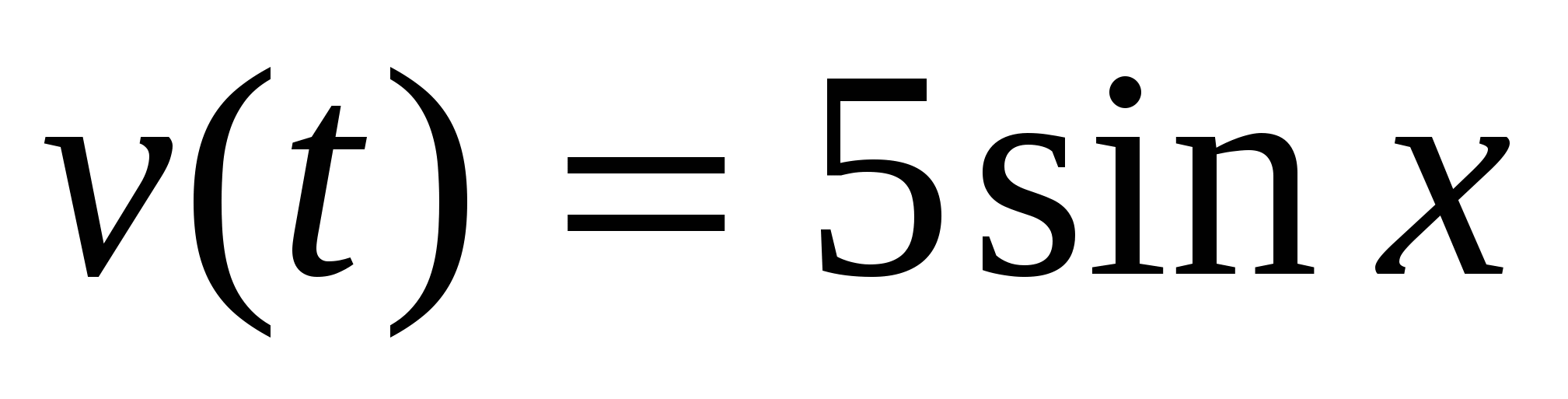. Найдите, ее ускорение в момент времени t=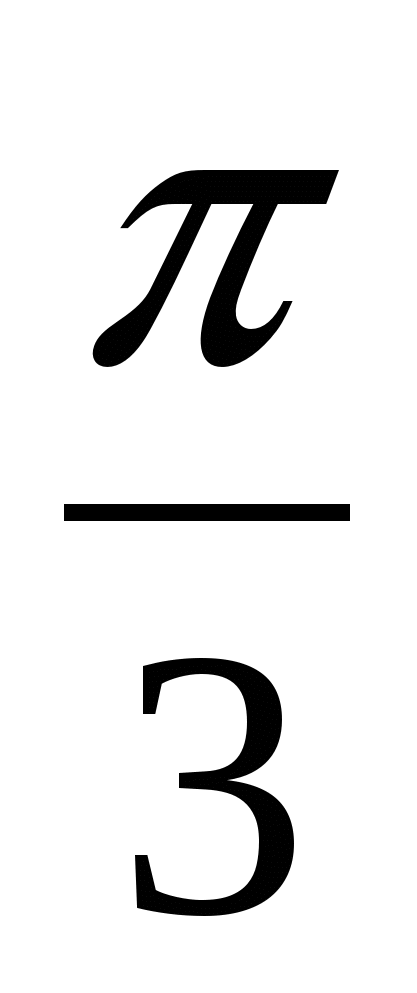с.

6. Зависимость пути от времени выражается формулой: 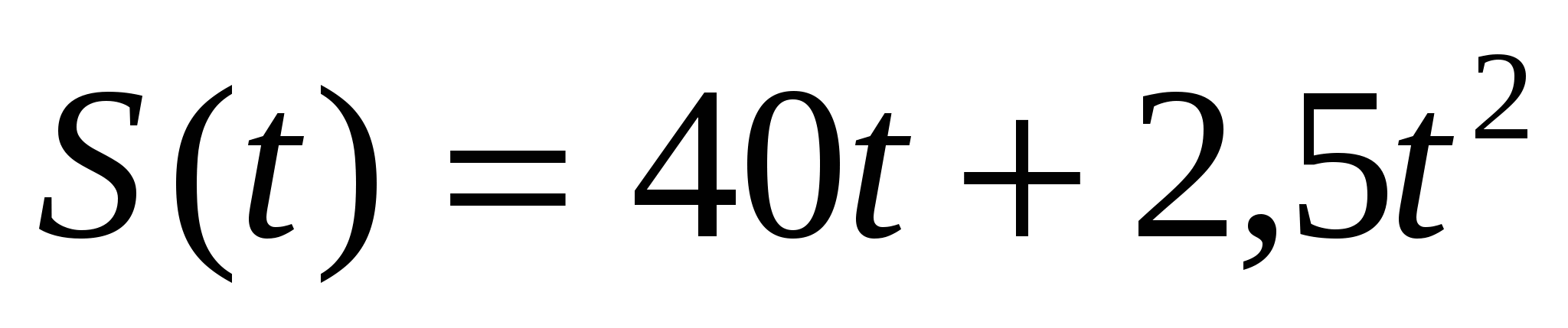. Найдите ее ускорение.

Ключ к шифрограмме.

У

К

Ц

Ф

О

М

Р

А

Н

П

Е

И

Т

2,5

-3

2

4,5

-1

4

5

1

-2

40

3

-5

Итог урока.

Используемая литература.

1. Дадаян А.А. Математика: Учебник для студентов образовательных учреждений СПО /А.А. Дадаян. – 2-е изд. – М.: Форум - Инфра-М, 2006. – 542,(1)с.: ил. – (Профессиональное образование).

Кол-во экз. -

2. Дадаян А.А. Сборник задач по математике: Учеб. пособие / А.А. Дадаян. – М.: Форум-Инфра-М, 2007 – 350с.: ил.

Приложение 1.

1 вариант.

1. Функция называется убывающей на промежутке (а;в), если на этом промежутке …

А) Большему значению аргумента, соответствует большее значение функции,

Б) ,

В) Меньшему значению аргумента соответствует меньшее значение функции,

Г) Большему значению аргумента соответствует меньшее значение функции.

2. Функция возрастает на промежутке (а;в), если на этом промежутке …

А) ,

Б) ,

В) ,

Г).

3. Если для любого х из промежутка (а,в) выполняется: 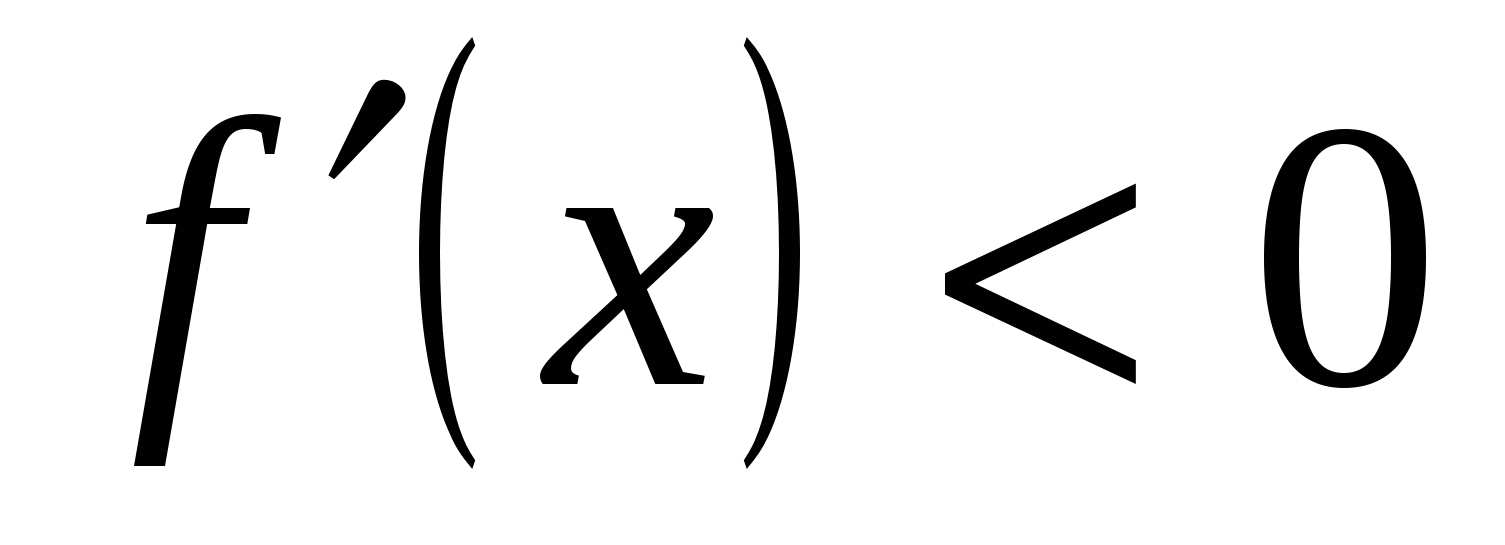, то на этом промежутке…

А) Убывание сменяется возрастанием,

Б) Функция убывает,

В) Функция возрастает,

Г) Имеет экстремум.

4. Точка х₀ является точкой минимума, если в ней …

А) ,

Б) Возрастание сменяется убыванием,

В) Убывание сменяется возрастанием,

Г) Нет верного ответа.

5. Минимум функции это –

А) Наименьшее значение функции,

Б) Минимально возможное значение функции,

В) Значение функции и точке минимума,

Г) Другой ответ

2 вариант.

1. Функция возрастает на промежутке (а,в) если на этом промежутке

А) Большему значению аргумента, соответствует большее значение функции,

Б) ,

В) Меньшему значению аргумента соответствует большее значение функции,

Г) Большему значению аргумента соответствует меньшее значение функции.

2. Функция убывает на промежутке (а;в), если на этом промежутке …

А) ,

Б) ,

В) ,

Г).

3. Если для любого х из промежутка (а,в) выполняется: 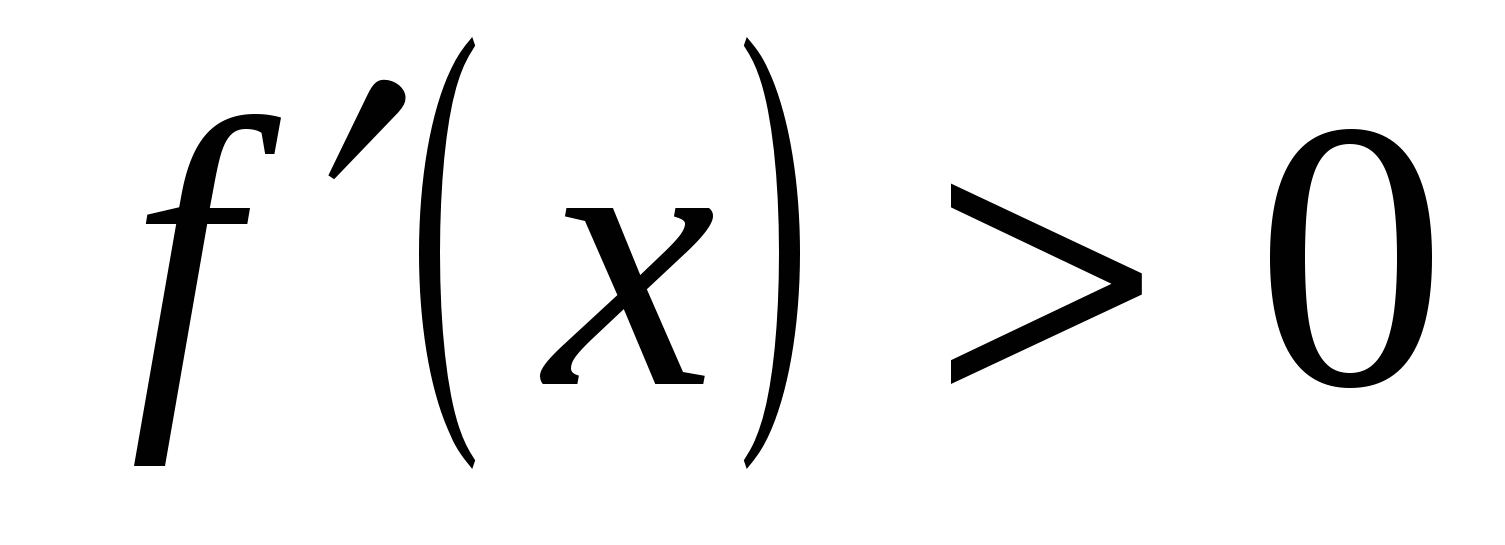, то на этом промежутке…

А) Функция возрастает,

Б) Функция убывает,

В) Возрастание сменяется убыванием,

Г) Имеет экстремум.

4. Точка х₀ является точкой максимума, если в ней …

А) ,

Б) Возрастание сменяется убыванием,

В) Убывание сменяется возрастанием,

Г) Нет верного ответа.

5. Максимум функции это –

А) Наибольшее значение функции,

Б) Максимально возможное значение функции,

В) Значение функции и точке максимума,

Г) Другой ответ.

Приложение 2.

ПРАКТИЧЕСКАЯ РАБОТА

ТЕМА: Исследование функции и построение графиков.

ЦЕЛЬ: Исследовать функцию по первой производной, построить ее график. Ответить на вопросы по графику.

1 вариант

Задача

1. Исследуйте функцию по первой производной и постройте ее график.

У=Х³ – 3Х – 1.

2. Ответьте по графику на вопросы.

   • Область определения функции?

   • Множество значений Функции?

   • Это четная или нечетная функция?

   • Это периодичная функция?

   • Нули функции?

   • Промежутки знакопостоянства?

   • Промежутки возрастания и убывания функции?

   • Точки максимума и минимума?

   • Максимум и минимум функции?

3. Домашнее задание. Дайте определения всех, вышеперечисленных понятий: Область определения, Множество значений, четная и нечетная функции, Периодичная функция, определение возрастающей и убывающей функций; Теоремы о возрастании и убывании функции на промежутке, Определение точек максимума и минимума, Максимум и минимум функции.

ПРАКТИЧЕСКАЯ РАБОТА

ТЕМА: Исследование функции и построение графиков.

ЦЕЛЬ: Исследовать функцию по первой производной, построить ее график. Ответить на вопросы по графику.

2 вариант

Задача

1. Исследуйте функцию по первой производной и постройте ее график.

У=2Х³ – 6Х + 2.

2. Ответьте по графику на вопросы.

• Область определения функции?

• Множество значений Функции?

• Это четная или нечетная функция?

• Это периодичная функция?

• Нули функции?

• Промежутки знакопостоянства?

• Промежутки возрастания и убывания функции?

• Точки максимума и минимума?

• Максимум и минимум функции?

3. Домашнее задание. Дайте определения всех, вышеперечисленных понятий: Область определения, Множество значений, четная и нечетная функции, Периодичная функция, определение возрастающей и убывающей функций; Теоремы о возрастании и убывании функции на промежутке, Определение точек максимума и минимума, Максимум и минимум функции.