Неравенства и уравнения, содержащие степень

Цель: провести систематизацию и обобщение знаний по вопросам решения уравнений и неравенств; рассмотреть и отработать решение более сложных уравнений и неравенств.

Ход урока:

1. Проверка домашнего задания.

1. Построить график функции

• 

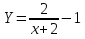
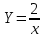
• Сдвиг графика функции 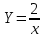на 2 единицы влево по оси Ох.

• Сдвиг графика функции 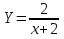на 1 единицу вниз по оси Оу.

2. Решить неравенство |3х-2|≥10

3х-2 ≤ -10 3х-2 ≥ 10

3х ≤ - 8 3х ≥ 12

х ≤ -2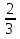 х ≥ 4

|5х-3| <7

-7 < 5х-3 < 7

-4 < 5х < 10

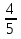- < х < 2

2. Повторение ранее изученного материала.

1. ах = в – линейное уравнение

• если а ≠ 0, х = 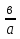- единственное решение;

• если а = 0, в ≠ 0, 0 · х = в – корней нет;

• если а = 0, в = 0, 0 · х = 0, х – любое число.

2. ах² + вх + с = 0, а ≠ 0

• (в² – 4·а·с) ≥ 0 – имеет корни;

• (в² – 4·а·с) < 0 – нет корней.

3. а^х = в – показательное уравнение

• х = log _а в, а > 0, в > 0, а ≠ 1.

4. а·х > в – линейное неравенство, решаем по свойствам числовых неравенств.

5. ах² + вх + с > 0, а ≠ 0

6. |х| > а, а ≥ 0

• х < -а; х > а

|х| < а, а ≥ 0

• -а < х < а.

3. Изучение нового материала.

1. х³ > 27

у = х³ – возрастает при любом значении х

х³ = 27

х =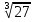

х = 3

х > 3.

х⁵ <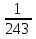

у = х⁵ – возрастает при любом значении х

х <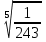

х < .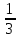

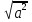2. = |а|

х² > 4

1 способ: х² > 4

при х ≥ 0, у = х² – возрастает

при х ≤ 0, у = х² – убывает

х² = 4

х_1,2 = ±2

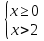
х > 2;

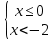
х < -2.

2 способ: х² > 4

|х| > 2

х > 2; х < -2.

3 способ (графический): х² > 4

у = х²

у = 4

график функции у = х² лежит выше графика функции у = 4, при

х > 2; х < -2.

3. Решение уравнения графически.

х³ = -х -2

у = х³ (о.о.ф. – множество R, функция является возрастающей на всей действительной оси, график симметричен относительно начала координат)

у = -х -2 (линейная функция, графиком является прямая, для построения достаточно двух точек)

х ≈ -1.

4. Решение иррациональных уравнений.

Иррациональное уравнение должно решаться либо с проверкой, либо нахождением области допустимых значений.

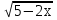= 1-х

5 – 2х = 1 – 2х + х²

х² = 4

х_1,2 = ±2

х = 2 – посторонний корень

х = -2.

4. Заключение. Выставление оценок. Домашнее задание