Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 15»

Конспект урока по теме:

«Правило умножения для комбинаторных задач »

Выполнила:

учитель математики

Галкина А.В.

Губаха 2010

Конспект урока составлен по учебнику: И.И. Зубарева, А.Г. Мордкович Математика 6

Цели:

1. Развивающая – развитие у учащихся умение самостоятельно формулировать правила, развитие логического мышления.

2. Обучающая – сформировать представление о комбинаторных задачах; научить строить дерево возможных вариантов.

3. Воспитательная – приучать учащихся к самостоятельной работе, воспитание взаимопомощи.

Задачи: формировать умения решать задачи по данной теме.

Оборудование: доска, мел, учебник, компьютер , проектор.

План урока:

1. Организационный момент

2. Подготовка к восприятию нового материала

3. Объяснение нового материала

4. Закрепление новых знаний

5. Домашнее задание

6. Итог урока

Ход

Урока

Деятельность

Учителя

Деятельность

Ученика

проектор

Доска

Организационный момент (0,5 мин)

-Здравствуйте! Настраиваемся на работу на уроке! Пожалуйста, садитесь!

Здравствуйте!

[садятся за парты]

1 слайд

22.12.10

Подготовка к восприятию нового материала (8 мин)

Начало нашего урока пройдет в несколько нестандартном виде. Вначале мы с вами побываем на уроке истории и узнаем о том, что за наука такая комбинаторика и откуда она к нам пришла.

Комбинаторика - ветвь математики, изучающая комбинации и перестановки предметов. Еще комбинаторику можно понимать как перебор возможных вариантов. Комбинаторика возникла в 17 веке. Долгое время она лежала вне основного русла развития математики.
С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов – во время битвы, инструментов - во время работы.
Комбинаторные навыки оказались полезными и в часы досуга. Нельзя точно сказать, когда наряду с состязаниями в беге, метании диска, прыжках появились игры, требовавшие, в первую очередь, умения рассчитывать, составлять планы и опровергать планы противника.
Со временем появились различные игры (нарды, карты, шашки, шахматы и т.д.). В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных. Не только азартные игры давали пищу для комбинаторных размышлений математиков. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв, заменах букв с использованием ключевых слов и т.д.
Комбинаторика как наука стала развиваться в 18 веке параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов. Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж.Кардано, Н.Тарталье (1499-1557), Г.Галилею (1564-1642) и французским ученым Б.Паскалю (1623-1662) и П.Ферма.
Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г.Лейбниц в своей работе “ Об искусстве комбинаторики ”, опубликованной в 1666 году. Он также впервые ввел термин “комбинаторика”. Значительный вклад в развитие комбинаторики внес Л.Эйлер. В современном обществе с развитием вычислительной техники комбинаторика “добилась” новых успехов.

[слушают учителя]

2 слайд

Объяснение нового материала (15 мин)

Ну вот мы и узнали о комбинаторике, но прежде чем приступить к решению задач по данной теме нам нужно познакомиться с некоторыми основными понятиями этой науки.

В задачах по комбинаторике часто применяется такое понятие как факториал (в переводе с английского “factor” - “множитель”).
Итак, произведение всех натуральных чисел от 1 до n включительно называют n-факториалом и пишут:

n!=1 2 3 … (n-1) n

Пример:
В комбинаторике решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. В зависимости от правил составления можно выделить три типа комбинаций:

1. Сочетания – сколько можно образовать сочетаний из n элементов по m.

2. Размещения – сколько можно образовать размещений из n элементов по m

3. Перестановки – это соединения, состоящие из одних и тех же элементов, отличающиеся только порядком расположения

Вот этих понятий нам будет достаточно для решения задач.

Ну а теперь можем смело приступать к решению комбинаторных задач.

На доске вы видите несколько табличек на которых написаны начальные буквы областей знаний, где применяется наука комбинаторика.

Разберем пару задач.

Первой решим задачу, которая скрывается под буквой М:

Как вы думаете какая область применения скрывается под этой буквой?

Светлана:

Правильно! Математика!

Вот условие:

Сколько трехзначных чисел можно составить из цифр 1, 3, 5, 7?
Используя каждую из них не более одного раза?

Решение:

(решаем)

Проведенный перебор вариантов проиллюстрирован на так называемом дереве возможных вариантов.

Ответ на поставленный в задаче вопрос мы нашли, используя комбинаторное правило умножения.

Ну что ж, молодцы давайте рассмотрим следующую карточку. Пусть это будет буква У:

Ваня, как ты думаешь какая здесь задача?

Это задача на управление, в данном случае в школе.

Условие задачи:

Из учащихся пяти 11 классов нужно выбрать двоих дежурных. Сколько пар дежурных можно составить (ученики в паре не должны быть из одного класса)?

Решаем:

[записывают в тетради]

[смотрят на доску]

Математика

(предполагает)

3 слайд

4 слайд

5 слайд

6 слайд

7 слайд

8 слайд

9 слайд

10 слайд

11 слайд

12 слайд

n!=1 2 3 …(n-1) n

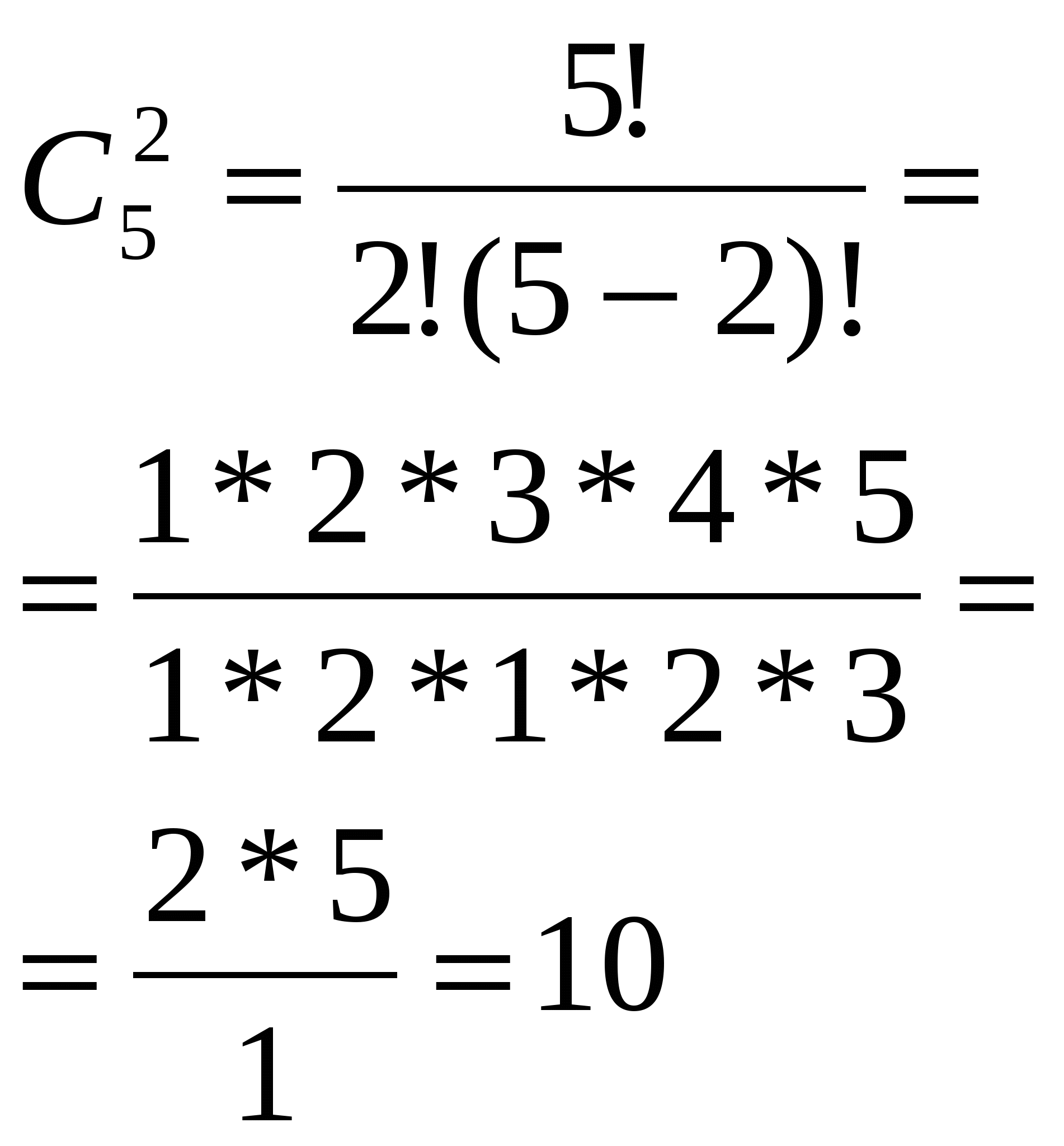
Закрепление новых

знаний (16 мин)

Ну а теперь вы сами попробуете решить любую задачу с моей помощью.

Даша к доске.

Какую букву выбираешь?

Как ты думаешь какую науку скрывает эта буква?

Молодец! Правильно!

Вот условие задачи:

Решаем 2 способами.

Спасибо! Молодец! Садись!

Ну что ж вы все сегодня хорошо поработали на уроке. (оценки)

(Даша идет к доске)

Даша выбирает букву Л

Я думаю логику

13 слайд

(Даша пишет решение)

Домашнее задание

(3 мин)

Итог урока (2 мин)

Откройте, пожалуйста, дневники, запишите домашнее задание.

Итак, что нового вы сегодня для себя открыли на нашем уроке?

Женя, Какие задачи называются комбинаторными?

правильно! Молодец!

Дима, что означает слово «комбинаторика»?

Правильно! Молодец!

Спасибо за урок! До свидания!

[открывают дневники и записывают домашнее задание]

[отвечают на вопрос]

Задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций, получили название комбинаторных.

Комбинаторика означает “соединять, сочетать”.

До свидания!

№ 497