Конспект урока по математике "Применение распределительного свойства умножения" 6 класс
Применение распределительного свойства умножения
Форма урока: Урок – путешествие. Тип урока: Урок обобщения и систематизации знаний. Цели урока:
Образовательная: систематизировать и обобщить известные учащимся сведения о распределительном свойстве умножения; выработать умения выполнять умножение дробных чисел, используя распределительное свойство умножения.
Развивающая: поддержать у учащихся интерес к изучаемому материалу на протяжении всего урока, активизируя работу учащихся за счёт использования на уроке различных форм работы. Развивать самостоятельность, внимание, математическое мышление.
Воспитательная: воспитание таких качеств личности как аккуратность в работе, трудолюбие, умение преодолевать трудности в процессе решения задач.
Методы обучения: фронтальная работа, самостоятельная работа, работа по вариантам. Оборудование: компьютер, проектор, экран, листочки с числами от 1 до 9, презентация, нарисованная карта.
ХОД УРОКА
I. Организационный момент. Постановка целей урока.
Здравствуйте, ребята, садитесь. Сегодня у нас необычный урок, урок-путешествие. А отправимся мы с вами к острову «Дробей». Но путешествие не обещает быть легким, ведь нам придется плыть по морю Сомнений, преодолев скалы Волнений, постараться не сесть на отмель Ошибок и не зацепить рифы Незнаний.
Давайте подумаем, чтобы путешествие было удачным, что нам надо взять с собой в дорогу, какие знания? (Ответы детей – правила умножения дробей, знание распределительного свойства умножения, и т. д.) Правильно, ребята, все это пригодится нам сегодня, мы повторим изученные правила и продолжим учиться применять их на практике.
II. Проверка домашнего задания.
Путешествие будет проходить на корабле (прикрепляется к карте к пункту «Старт»). Билетом на корабль послужит правильно выполненное домашнее задание. (Проверка ДЗ по ответам, дети в тетрадях ставят «+» за правильно выполненный номер, «-» - за неправильный.)
№553(г)
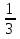 х +
х + 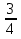 х -
х - 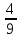 х =
х = 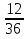 х +
х + 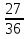 х -
х - 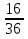 х =
х = 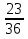 х
х
Если х=1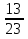 , то
, то 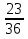 ·
·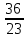 =1
=1
Если х=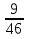 , то
, то 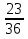 ·
·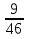 =
=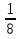
№555
1 ящ - 12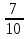 кг
кг
2 ящ - ?, в 2 раза больше; станет после добавления 2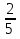 кг - ?
кг - ?
Решение:
12
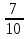 ·2=12·2+
·2=12·2+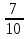 ·2=24+
·2=24+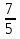 =25
=25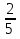 (кг) – во 2 ящ.
(кг) – во 2 ящ.25
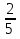 +2
+2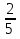 =27
=27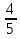 (кг) – станет во 2 ящ.
(кг) – станет во 2 ящ.
Ответ: 27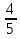 (кг)
(кг)
№560(а)
(3,75:1,25-0,75):1,5+0,75=(3-0,75):1,5+0,75=2,25:1,5+0,75=1,5+0,75=2,25.
Итак, команда сформирована, отправляемся в путь!
III. Актуализация знаний. Устный счет.
В начале путешествия нам надо выбрать капитана. Думаю, справедливо будет считать капитаном того, кто даст больше правильных ответов на задания «Устного счета» - первого этапа нашего плавания. Необходимо найти ошибки, исправить их, объяснить.
2
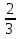 ·4=2·4+
·4=2·4+ 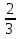 =8
=8 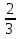
1
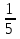 ·5=1+
·5=1+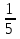 ·5=1+
·5=1+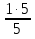 =1+1=2
=1+1=23
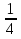 ·2
·2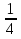 =3·2+
=3·2+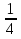 ·
·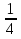 =6+
=6+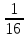 =6
=6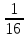
5
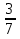 ·7=5·7+
·7=5·7+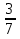 ·7=35+3=38
·7=35+3=38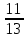 ·3=
·3=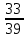
(
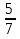 )²=
)²=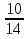
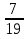 ·2=
·2=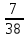
IV. Тренировочные упражнения. Решение задач.
Итак. скалы Волнений мы благополучно миновали, идем дальше (корабль «движется» по карте к пункту «1»). Зачем нам знания, которые мы получаем в школе? Правильно, чтобы в нужный момент их применить. Сейчас у вас замечательная возможность применить свои знания правил умножения дробей. Предлагаю каждому варианту решить по одной задаче, первому - №526, второму - №527, два человека решают задачу за доской, затем проверка с объяснением.
№526
Б – 150лет
С - ?, в 2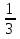 раза больше березы
раза больше березы
М - ?, в 5 раз дольше сосны
Решение:
150·2
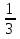 =300+50=350(л) – сосна
=300+50=350(л) – сосна350·5=1750(л) – мамонтово дерево
Ответ: 1750 лет
№527
Длина б.к. - 5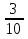 м
м
Ширина б.к. – 4м
Длина м.к. – 4 м
Ширина м.к. - 3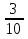 м
м
Разница площадей-?
Решение:
5
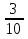 ·4=21
·4=21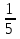 (м²)- площадь б.к.
(м²)- площадь б.к.4·3
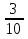 =13
=13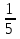 (м²) – площадь м.к.
(м²) – площадь м.к.21
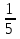 - 13
- 13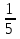 = 8(м²) разница площадей
= 8(м²) разница площадей
Ответ: 8 м²
Кто решил №527 другим способом? Обсудить.
V. Закрепление знаний изученных правил.
Правильно решив задачи, мы не сели на отмель Ошибок и движемся дальше! (Корабль в пункте «2») Предлагаю еще раз вспомнить правила действий с дробями. У вас на столах лежат листочки с цифрами от 1) до 9).
1)
2)
3)
4)
5)
6)
7)
8)
9)
Я зачитываю вопрос, если он верный то напротив соответствующего номера ставите “+”, если неверный, то “-”.
Тест
При сложении дробей с одинаковыми знаменателями знаменатель остается тем же, а числители складываются.(+)
Чтобы вычесть дроби с разными знаменателями, надо привести их к наибольшему общему знаменателю и выполнить вычитание дробей с одинаковыми знаменателями.(-)
При сложении целого числа и смешанного получается смешанное число.(+)
Чтобы выделить целую часть из неправильной дроби, надо числитель умножить на знаменатель.(-)
Если при сложении дробей получается неправильная дробь, то надо результат записать в виде смешанного числа.(+)
Произведение двух дробей есть дробь, в числителе которой произведение знаменателей, а в знаменателе – произведение числителей.(-)
Чтобы из единицы вычесть дробь, надо единицу записать в виде неправильной дроби со знаменателем, равным знаменателю дроби, которую вычитаем.(+)
При умножении двух смешанных дробей, надо перемножить целые части и сложить с произведением дробных частей.(-)
При умножении целого числа на дробь, надо целое число умножить на числитель, а знаменатель оставить прежним.(+)
Соедините знаки «+», расположенные по одной линии. Что получили? Каким образом полученный символ связан с математикой? Где он нам встречается? Правильно, это х – неизвестное в уравнении. И, конечно, нам не миновать решения уравнений, если мы хотим добраться до цели нашего путешествия. Наш корабль тем временем перемещается в пункт «3».
VI. Решение уравнений с использованием распределительного свойства умножения.
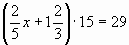 , 6x + 25 = 29, 6x = 29 – 25, 6x = 4, x =
, 6x + 25 = 29, 6x = 29 – 25, 6x = 4, x = 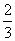 , Ответ:
, Ответ: 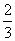 .
.
Дополнительные уравнения на карточках:
(
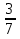 х + 2
х + 2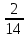 )·28=72 (х=1)
)·28=72 (х=1)(
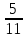 х - 1
х - 1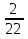 )·44 = 12 (х=3)
)·44 = 12 (х=3)(
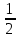 -
- 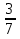 х)·14 = 6 (х=
х)·14 = 6 (х=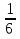 )
)28х·1
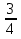 - 28х·
- 28х·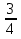 = 1 (х=
= 1 (х=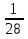 )
)
Вы замечательно справились и с этим испытанием, остался последний, самый опасный пункт – рифы Незнаний, желаю всем благополучно их преодолеть, выполнив задания самостоятельной работы, но перед этим предлагаю сделать небольшую паузу, послушать историческую справку.
Из истории дробей.
Дроби появились в глубокой древности. При разделе добычи, при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести дроби, так как результат измерений не всегда удавалось выразить натуральным числом, приходилось учитывать и части употребляемой меры.
Древние египтяне использовали дроби, у которых в числителе стояла 1 – так называемые основные дроби – ½, 1/3, 1/28 и т.д. Если египтянину нужно было использовать другие дроби, он представлял их в виде суммы основных дробей. Например, вместо 8/15 писали 1/3+1/5.
В древнем Вавилоне предпочитали наоборот, - постоянный знаменатель, равный 60-ти. Шестидесятеричными дробями, унаследованными от Вавилона, пользовались греческие и арабские математики и астрономы.
Знание дробей считалось очень важным, ещё в первом веке до нашей эры выдающийся римский оратор и писатель Цицерон говорил: “Без знания дробей никто не может признаваться знающим арифметику!”
Наше обозначение обыкновенных дробей при помощи числителя и знаменателя было принято в Индии еще в VIII веке до н.э. однако без дробной черты. Только там писали знаменатель сверху, а числитель – снизу.
А записывать дроби в точности, как сейчас, стали арабы.
VII. Самостоятельная работа.
Задания из дидактического сборника. 1 вариант – стр 39, №127, №129, 2 вариант – стр 67, №127, №129.
VIII. Подведение итогов. Домашнее задание.
Достигнув конечной точки нашего маршрута, давайте подведем итоги, насколько успешно мы разрешили встретившиеся на нашем пути проблемы? Кто с чем пришел к финишу?
Выставление оценок.
Задание на дом: №552(д,е), №559.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ