МИНИСТЕРСТВО ОБРАЗОВАНИЯ и НАУКИ РЕСПУБЛИКИ КАЗАХСТАН.

Открытый урок

По математике в 5 классе

НА ТЕМУ:

«Умножение обыкновенных дробей»

Разработала и провела урок

Учитель математики:

Ведяева А. Г.

.

2009-1010 учебный год.

Цели урока:

- сформировать понятие умножения дробей;

- способствовать формированию умений применять знания в новой ситуации, развитию математического кругозора, мышления и речи, внимания и памяти;

- содействовать воспитанию интереса к математике, активности творчества.

Оборудование:

- компьютеры,

- записи на доске,

- учебник «Математика-5» (Т.А. Алдамуратова, Е.С. Байшолан.),

Ход урока.

Время урока.

1. Мотивация. Сообщение темы, целей и плана урока.

3 мин

(Обратить внимание учащихся на эпиграф.)

«Не только в жизни богов и демонов
раскрывается могущество числа.»
Пифагор

Учитель: С 1-го класса вы изучаете числа и их свойства. Чисел так много, что невозможно назвать ни наибольшего, ни наименьшего из них. Однако все числа связаны между собой. Мы уже знакомы с натуральными числами, умеем выполнять сложение, вычитание, умножение и деление этих чисел. В этом году мы изучаем обыкновенные дроби и уже научились складывать и вычитать их. Впереди нас ждет знакомство еще с одним действием над обыкновенными дробями – умножением. Сегодня мы должны вспомнить и повторить все, что мы уже знаем об обыкновенных дробях.

На уроке каждый из вас должен получить оценку, которую сами будете конструировать за выполнение отдельных видов работ.

Вопрос:

1. Сколько половинок ( долей) содержится в целом круге?

2. Сколько четвертинок ( долей) содержится в целом круге?

ЖЕЛАЮ ВАМ ВСЕМ УСПЕХА!

Проверку выполнения домашнего задания провести до начала урока.

2. Для того, чтобы вы включились в урок, я прочитаю вам одну из научных сказок Феликса КРИВИНА “Простая дробь”, а вы должны ответить на вопрос: “О каком свойстве дробей в ней говорится?” .

8 мин

“У Числителя и Знаменателя – вечные дрязги. Никак не поймешь, кто из них прав. Числитель толкует одно, а Знаменатель перетолковывает по-своему.

Числитель говорит:

- У меня положение выше, почему же я меньше Знаменателя?

А Знаменатель своё:

- Я-то числом побольше, с какой стати мне ниже Числителя стоять?

Поди, рассуди их попробуй!

И ведь что вы думаете – была такая попытка. Целое Число, которому надоело это брюзжание, сказало им напрямик:

- Склочники несчастные, чего вы не поделили? В то время, когда у нас столько примеров, столько задач ….

-Тебе, Целому, хорошо, - проворчал Знаменатель, и Числитель (в первый раз) согласился с ним.

- Знаменательно! – воскликнул Числитель. – Знаменательно, что именно Целое Число делает нам замечание!

- А кто мешает вам стать Целым Числом? Сложитесь с какой-нибудь дробью.

- Ладно, обойдемся без ваших задач и примеров, - сказал Числитель, а Знаменатель, придвинувшись к Целому Числу, выразил эту мысль более категорически:

- Проваливай, пока цело!

Целое Число махнуло на них рукой и приступило к очередным задачам.

А Числитель и Знаменатель призадумались… Потом Числитель нагнулся, постучал в черточку:

- Послушайте, - говорит, - может, нам и впрямь с другой дробью сложиться?

- Э, шалишь, брат, - возразил Знаменатель, - хватит с меня и одного Числителя.

- Если уж на то пошло, - обиделся Числитель, - мне тоже одного Знаменателя предостаточно.

Ещё подумали.

Потом Знаменатель встал на цыпочки, постучал в черточку:

- Слышь, ты! А если нам стать Целым Числом, без другой дроби?

- Можно попробовать, - соглашается Числитель.

Стали они пробовать. Числитель умножился на два, и Знаменатель – не отставать же! – тоже на два. Числитель на три – и Знаменатель на столько же.

Умножались, умножались, совсем изнемогли, а толку никакого. Та же дробь, ни больше ни меньше прежней.

- Стой! – кричит Знаменатель. – Хватит умножаться. Делиться давай. Так оно вернее будет.

Стали делиться.

Знаменатель на два – и Числитель на два, Знаменатель на три – и Числитель на столько же. А дробь….?»

Ответ. Основное свойство дроби: ”Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.”

3. Фронтальное повторение теоретического материала.

3 мин

- Что называют сокращением дроби?

- Какую дробь называют несократимой?

- Как найти дополнительный множитель?

- Какая дробь называется правильной?

- Какая дробь называется неправильной?

- Как из неправильной дроби выделить целую часть?

- Как записать число в виде неправильной дроби?

4. Устный счет.

2мин

Задания.

Сократить дробь

Выделить целую часть числа

Записать число в виде неправильной дроби

Вычислить 1-

Найти сумму дробей

5. Объяснение нового материала.

15 мин

Работа с компьютером

Физкультминутка

Поднимает руки класс — это «раз».

Повернулась голова — это «два».

Руки вниз, вперед смотри — это «три».

Руки в стороны пошире развернули на «четыре»,

С силой их к плечам прижать - это «пять».

Всем ребятам надо сесть — это «шесть».

1 мин

8 мин

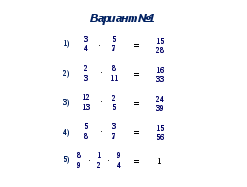
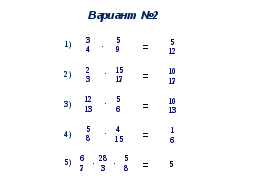
Задания соответствуют уровням сложности:

- уровень А

- уровень В

- уровень С

При быстром выполнении заданий сильные ученики проверяют свои умения с помощью программы «fraction»- Арифметические действия с обыкновенными дробями 2.1.

8. Итог урока. Выставление оценок.

3 мин

Д/З: №773 (1-4).

Учитель: Сегодня на уроке мы неплохо поработали. Благодарю всех. Закончить урок мне хочется словами Л.Н. Толстого:

«Человек есть дробь. Числитель - это сравнительно с другими - достоинства человека; знаменатель – это оценка человеком самого себя. Увеличить своего числителя – свои достоинства, не во власти человека, но всякий может уменьшить своего знаменателя – свое мнение о самом себе, и этим уменьшением приблизиться к совершенству.” Задумайтесь над этими словами.

2 мин