Бюджетное общеобразовательное учреждение

города Омска

«Средняя общеобразовательная школа № 107»

Квадратные уравнения

(Повторение)

подготовила

учитель математики

Муравьева Татьяна Алексеевна

г. Омск 2012

«Квадратные уравнения. Повторение».

с использованием парацентрической технологии обучения

(математика, 9 класс)

Технологическая карта темы «Уравнения. (Повторение)» по алгебре в 9 классе.

Логическая структура учебного процесса

Ц₁ Д₁ К₁ Ц₂ Д₂ К₂ Ц₃ Д ₃К₃ Ц₄ Д ₄К₄ К_п

1

2

3

4

5

6

7-8

1. Линейные уравнения (1час). Обобщение и систематизация.

3. Квадратные уравнения (2 часа). ПЦТО.

5. Дробно-рациональные уравнения (2 часа). ПЦТО.

6. Иррациональные уравнения (1 час). Обобщение и систематизация.

8. Письменный контроль (2 часа).

Линейные уравнения.

Целеполагание

Дата

Диагностика

Дата

Коррекция

Ц₁ Повторить понятие линейного уравнения, свойства уравнения, систематизировать и обобщить сведения о решении уравнения с одним неизвестным.

Уметь: решать уравнения, сводящиеся к линейным, исследовать вопрос о числе корней линейного уравнения.

Знать: определение линейного уравнения, свойства уравнений.

ВП: Арифметическая прогрессия. Показательные, логарифмические уравнения. Нахождение области определения функции.

МП: Физика (выразить одну величину через другую, составить и решить пропорцию).

Химия (уметь выражать одну переменную через другую, химические уравнения, расчеты по уравнениям).

ОУУН: Умение выделять, сравнивать, обобщать, систематизировать учебный материал. Осуществлять самоконтроль и давать самооценку своей учебной деятельности.

1 урок

Д₁

Самостоятельная работа 1.

Уровень А

1.Решить уравнение

3у-(5-у)=11.

2. При каких а уравнение ах=8 имеет корень х=0, х = -4?

3. Решите задачу, составив уравнение.

Поезд был задержан в пути на 1 час. Увеличив скорость на 30 км\ч, он через 3 часа прибыл на конечную станцию точно по расписанию. Чему была равна скорость поезда до остановки?

Уровень Б

1.Решить уравнение

(7х+1)-(6х+3)=3(2х+5).

2. При каких а уравнение ах=8 имеет положительный, отрицательный корень?

3. Решите задачу, составив уравнение.

Поезд прошел первый перегон за 2 часа, второй за 3 часа. Всего за это время он прошел 330 км . Найдите скорость поезда на каждом перегоне, если на втором она была на 10км\ч больше, чем на втором.

Самостоятельная работа 2. (Сборник заданий для проведения экзамена за 9 класс. Дрофа. 2005.)

Уровень А

Уровень Б

№339, 361, 380, 368.

№343, 362, 384, 378.

К₁

Затруднения и ошибки

1. Раскрытие скобок.

2. Перенос слагаемых.

3. Приведение подобных.

Способы устранения

1. Решить уравнение

- 8х=-24;

3х =;

- =.

2. Решить уравнения

3х+7=0;

7х-4=х-16;

3. Среди данных уравнений укажите те, которые не имеют корней:

3х+7=3х+11;

5-х=6-х;

│ х │=8;

│х │+1=0.

4. Выразите каждую из букв, входящих в формулу, через остальные: vt=s, mg=P, IR=U.

Квадратные уравнения.

Целеполагание

Дата

Диагностика

Дата

Коррекция

Ц ₂ Обобщить и систематизировать умения решать квадратные уравнения и уравнения, сводящиеся к ним.

Уметь: решать квадратные уравнения; уравнения, сводящиеся к квадратным и применять их к решению задач; исследовать на количество корней при различных значениях параметра.

ВП:Тригонометрические, показательные и логарифмические уравнения. Геометрическая прогрессия. Исследование функций. Производная и применение производной к исследованию функции.

МП: 10-11 кл. Кинематика. Колебания. Волны. Термодинамика. Электромагнетизм.

ОУУН: Умение выделять, сравнивать, обобщать, систематизировать учебный материал. Осуществлять самоконтроль и давать самооценку учебной деятельности.

2-3 уроки

Д ₂

Самостоятельная работа.

Уровень А

1.Каждое уравнение соотнеси с количеством корней

1) х²-5х+6=0;

2) 3х²+4=0;

3) х²+2х+1=0.

а) 1; б) 2; в) 0.

2. Приведи к квадратному уравнению

1) (х+3)(х-3)=2(х-0,5)4

2)

3.Составь квадратное уравнение, корни которого равны -3 и 2.

4. Найди корни квадратного трехчлена подбором и разложи его на множители

1) х²+5х+6;

2) х²+2х-15.

5.При каких значениях с уравнение х²+2х+с=0 имеет один корень?

6 .Деревенский домик длины 9м и ширины 7м обрамлен садом постоянной ширины (см. рис.). Сад без домика занимает площадь, равную 512м². Какова ширина сада?

7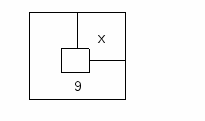

1) (х+7)(х+9)=512

2) (2х+7)(2х+9)=512

3) (х+7)(х+9) - 63=512

4) (2х+7)(2х+9) - 63=512

Уровень Б

1.Каждое уравнение соотнеси с количеством корней

1) (2х²+1)(х²+3х-4)=0;

2) (6х²-4)(9х²-12х+4)=0;

3) 8х²(х²+х+5)=0.

а) 1; б) 2; в) 3.

2. Приведи к квадратному уравнению

1) (3х+2)²-(2х-1)² =0;

2)

3 .Составь квадратное уравнение, корни которого равны -2 и -0,5 .

4 . Не вычисляя корней х₁ и х₂ уравнения х²-8х-15=0 найти

а) ; б) (х₁+х₂)².

5 .При каких значениях с уравнение х²+6х+с=0 не имеет корней?

6.Картина прямоугольной формы обрамлена рамкой ширины 3см (см.рис.). Одна сторона картины на 6см больше другой. Картина вместе с рамкой занимает площадь, равную 567см². Найдите параметры картины. Выберите уравнение, соответствующее условию задачи.

х

3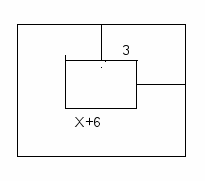

1) (х+3)(х+6)=567

2) (х+3)(х+9)=567

3) х(х+6)=567

4) (х+6)(х+12)=567

К ₂

Затруднения и ошибки

1. Формулы сокращенного умножения

2.Раскрытие скобок

3.Формула нахождения корней квадратного уравнения

Способы устранения

1. Корректирующие задания с пропусками

а) Заполни пустые клетки

х²-6х+ =(х- )²

х²+2 х+ =(х+5)² 4х²+8х+ =( + )²

б)Заполни пропуски так, чтобы данное уравнение было квадратом суммы или разности

х²-4х+ ; х²-7х+

х²- х+81

2. Заверши решение уравнение

х²+4х-12=0

а=1, в=4, с=-12

х_1,2==…

Дробно – рациональные уравнения.

Целеполагание

Дата

Диагностика

Дата

Коррекция

Ц₃:обобщить и систематизировать умения решать дробно-рациональные уравнения.

Знать: алгоритм решения дробно-рациональных уравнений.

Уметь: Решать дробно-рациональные уравнения и применять их к решению задач.

ВП: 10-11 кл. Логарифмические, показательные и тригонометрические уравнения. Производная. Исследование функции.

МП: 10 кл. Физика. Принцип суперпозиции электромагнитных полей.

ОУУН: Умение выделять, сравнивать, обобщать, систематизировать учебный материал. Осуществлять самоконтроль и давать самооценку учебной деятельности.

4-5 уроки

Д ₃

1⁰

Диктант

1.Решите уравнение

2.Решите уравнение

3.Переменная может принимать значения -3,1,2,4. При каких из этих значений х верно неравенство х-1.

4. При каких значениях переменной равны дроби

и .

5.Составьте уравнение по условию задачи.

На движение по реке от города А до города В и обратно катер Тратит 12 часов. Найти скорость катера в стоячей воде, если скорость течения реки 1 км\ч, а расстояние от А до В равно 70км.

2⁰

Тест

1. Определите корни данного уравнения .

а) 7; -2. б) 7. в)3,5. г)3,5;-2.

2. Решите уравнение

а)0;2. б) 0;-2. в)-2. г)2.

3. Решите уравнение

а) 2; 9. б) 4; 18. в)-4; -18. г)8; 36.

4. Произведение двух последовательных чисел равно 182. Найдите сумму этих чисел.

а)27. б)36. в)24. г)42

5. Моторная лодка прошла 10 км по озеру и 4 км против течения реки, затратив на весь путь 1 час. Найдите собственную скорость лодки, если скорость течения реки 3 км\ч.

а)15км\ч или 2 км\ч.

б) 15км\ч. в)30 км\ч.

г)правильного ответа нет.

К₃

Затруднения и ошибки :

1. Вычислительные навыки.

2. Приведение дробей к общему знаменателю.

3. включение в ответ посторонних корней.

Способы устранения:

1. Опорный конспект.

2. Конкретные задания

а) привести дроби к общему знаменателю:

; и .

и.

и.

и.

,

и.

б) при каких значениях х имеет смысл выражение.

в) проверьте, являются ли числа 3;-6;0 корнями уравнения.

Иррациональные уравнения

Целеполагание

Дата

Диагностика

Дата

Коррекция

Ц₄

Обобщить и систематизировать сведения об иррациональных уравнениях

Знать: алгоритм решения иррационального уравнения.

Уметь: рашать иррациональные уравнения, выбирать наиболее предпочтительные способы их решения.

ВП:10-11кл. Иррациональные уравнения и неравенства. Логарифмические и показательные уравнения. Производная. Исследование функции.

МП: Электромагнитные и механические колебания.

6 урок

Д₄

1⁰

Диктант

1. Указать номера уравнений, которые являются иррациональными:

а) х +=2; б) х;

в) у +

г) д) у²-3у=4

2. Является ли число х₀ корнем уравнения:

3. Не решая следующих уравнений, объясните, почему каждое из них не может иметь корней:

а)

б)

4. найдите область определения функции:

а) у =

б) у =

в)

2⁰

Самостоятельная работа

1. Решите уравнение:

а); а) ;

б); б) ;

в) в); в) ;

г) ;

;

д)

2. Выясните, при каких значениях х имеет место равенство

а) ;

б)

3⁰

Тест

1. Определите область допустимых значений неизвестного в уравнении

а) 0<х <3; б) -3

в) х

2. Решите уравнение

а) х=10; б) решений нет;

в) х₁=10; х₂=11.

3.Решите уравнение

а) х =1; б) х₁=1; х₂=-1;

в) х = -1; г) решений нет

К₄

1⁰

Затруднения и ошибки

1. Вычислительные навыки.

2. Формулы сокращенного умножения.

3. Включение в ответ постороннего корня.

Способы устранения

1. Опорный конспект.

2. Конкретные задания (корректирующие задания с пропусками):

а) заполни пропуск так, чтобы получился квадрат суммы или разности

с²+4с+

36 с²- +49х²

Р²- 0,5р+

х²-6ху+

б) представьте в виде многочлена:

(х-у)²; (2+х)²; (6а-4в)²; (0,2х+0,3у)²

3.Обратить внимание учащихся на необходимость проверки.

2⁰

Затруднения и ошибки

1. Вычислительные навыки.

2. Приведение подобных слагаемых.

3. Раскрытие скобок.

4. Включение в ответ постороннего корня.

Способы устранения

1. Раскройте скобки

а) (х-17)(х+1)

б) (х+8)(х-6)

в) (2х+1)(2х-3)

г) (2х-7)(3х-4)

2. Приведите подобные слагаемые

а) 3х²-18х+3-15х-х²+8;

б) –х²+3х³-4х+6х-18х²

Обратить внимание на необходимость проверки.

3⁰

Затруднения и ошибки

1. Формулы сокращенного умножения.

2. Алгоритм решения иррационального уравнения.

3. Включение в ответ постороннего корня.

Способы устранения.

1. Конкретные задания

а) Решить уравнения

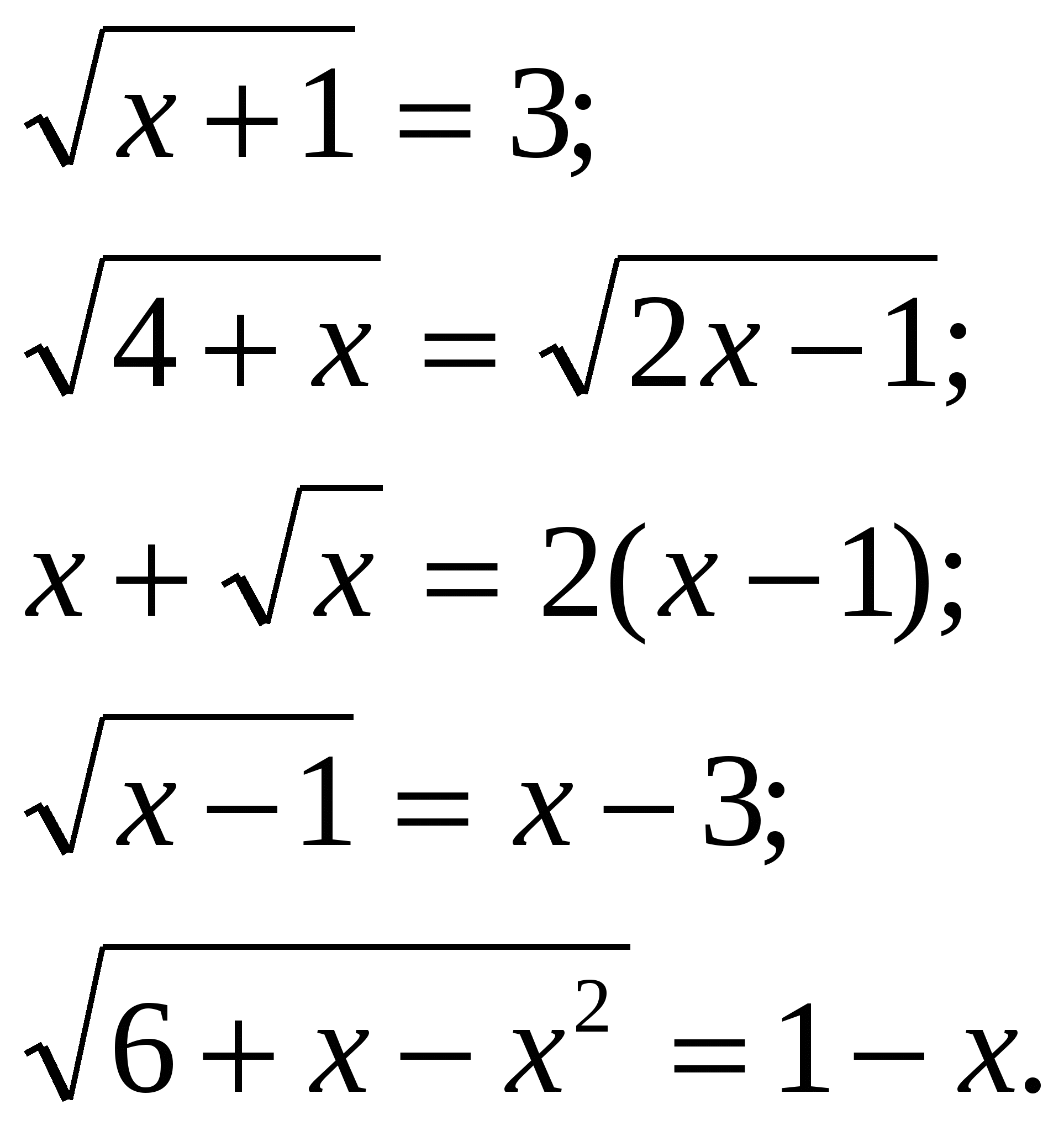
б) напомнить учащимся о необходимости проверки.

Письменный контроль уроки 7-8.

Урок алгебры в 9 классе по теме

«Квадратные уравнения (повторение)», разработанный

с использованием парацентрической технологии обучения.

Целеполагание (см технологическую карту).

Этапы урока

Деятельность учителя

Деятельность учащихся

1.ИВУ

9.55-10.05

(10 мин)

Здравствуйте, ребята! Тема нашего занятия «Квадратные уравнения».

Запишите число, тему урока.

Квадратным уравнением в школьном курсе математики придается большое значение; для них доказываются теоремы, выводятся формулы, безукоризненное знание которых требуется от каждого выпускника основной школы. И вы, я уверена, знаете почему. Умение решать квадратные уравнения применяется практически во всех темах алгебры, а также при решении многих геометрических задач, кроме этого при изучении отдельных тем курса физики, химии.

Когда речь заходит о квадратных уравнениях, на память приходят слова английского поэта Джефри Чосер:

Посредством уравнений теорем

Он уйму всяких разрешил проблем: И засуху предсказывал и ливни.

Поистине его познанья дивны.

Вы, ребята, тоже накопили опыт решения различных задач с помощью квадратных уравнений.

Сегодня вам предстоит разрешить пусть не уйму, но 5-6 проблем. Помощником нам послужит ПЦТО. Это означает обучение в парах со средством обучения при помощи методических инструкций и последующим выходом для собеседования с учителем. СО сегодня – это карточки, тексты, учебные пособия, сборники задач.

На столе у каждого из вас лежит лист контроля, в котором прописаны те знания и умения, которые сегодня вы должны повторить с помощью соответствующих средств обучения.

Далее учитель знакомит с целями, информационным листом, возможностями СО, алгоритмом работы по ПЦТО.

Воспринимают информацию.

2. ОВУ

10.05-10.15

(10 мин)

Корректирует индивидуальные маршруты учащихся.

Выбирают СО, заполняют верхнюю строчку листа контроля.

3. Работа со средствами обучения

10.15-10.40

10.50-11.10

(45 мин, перемена 10мин).

Наблюдает, консультирует, контролирует.

Работают со СО, консультируются с учителем, консультантом.

4. Обобщение и систематизация 11.10-11.20 (10мин)

Организует фронтальный диалог с учащимися по результатам работы:

• Что знаем о квадратных уравнениях? Что умеем?

• Где вы сегодня применяли эти знания и умения?

• При выполнении каких заданий возникали трудности?

• Как вы их преодолевали?

• Оценочная шкала (заранее написана на доске):

27 и больше баллов «5»

21-26 баллов «4»

15-20 баллов «3»

меньше 15 баллов «2»

Учащиеся отвечают.

5. Диагностика

11.20-11.35 (15мин)

Предлагает диагностику в форме самостоятельной работы.

Проверка ответы на доске, взаимопроверка. Тетради учащиеся сдают.

Выполняют работу, оценивают друг друга.

Предлагает домашнее задание (внеаудиторная самостоятельная деятельность учащихся):

Уровень образовательного стандарта

Уровень повышенной сложности

Высокий уровень

№73, 95 по сборнику задач для проведения экзамена ,

№603 по учебнику Алимова.

№77, 78,82,96, 97,99 по сборнику задач для проведения экзамена,

№ 621(2,4),

622(чет) по учебнику Алимову.

№777, 799 по учебнику Алимова

Информационный лист для учащихся

Шифр

Задание

Название

Кол-во баллов

Контроль

СО 1

Решить уравнение по алгоритму

Карточка №1

2

Самопроверка

СО 2

Уравнения, сводящиеся к квадратным (содержат скобки, числовой знаменатель)

Карточка №2

4

В паре + ответ

СО 3

Карточка №3

6

Промежуточные результаты + ответ

СО 4

Уравнения, сводящиеся к квадратным (биквадратные)

Схема №1,2

3

Ключ на столе учителя

СО 5

Карточка №4

6

Образец на столе учителя

СО 6

Разложение на множители квадратного трехчлена

Карточка №5

3

Самопроверка

СО 7

Задания с использованием теоремы Виета

Карточка №6

3

На столе учителя

СО 8

Карточка №7

5

У консультанта

СО 9

Текстовая задача

Текст №1

4

В паре

СО 10

Математика. Алгебра. Функции. Анализ данных.

8 класс. Г.В. Дорофеев .

5

С решебником учителя

СО 11

Задания с параметром

Карточка №8

4

Консультант

СО 12

Карточка №9

6

Учитель

СО 13

Уравнения, решаемые способом замены переменной

Карточка №10

6

Консультант

СО 14

Рурукин или письменно

6

Учитель

Лист учета результатов деятельности учащихся

СО

1

СО

2

СО

3

СО

4

СО

5

СО

6

СО

7

СО

8

СО

9

СО

10

СО

11

СО

12

СО

13

СО

14

Всего баллов

2

4

6

3

6

3

3

5

4

5

4

6

6

6

Знать и уметь:

1.Алгоритм решения кв.уравнений

●

2. Алгоритм решения уравнений, сводящихся к квадратным:

а) содержит скобки, числовой знаменатель;

б) уравнения, решаемые способом введения новой переменной

• биквадратные

• другая замена

●

●

●

●

●

●

Раскладывать на множители квадратный трехчлен

●

Применять теорему Виета

●

●

Составлять уравнения по условию задачи и решать его

●

●

Решать задачи с параметром

●

●

КАРТОЧКА №1

МИ 1. Запиши формулу для нахождения корней квадратного уравнения. Реши предложенные уравнения и соотнеси с множеством его корней. Сверь свой ответ с ответом на обратной стороне карточки.

СО 1.

1 вариант

1. 3х²+5х-8=0 а) нет корней

2. х²+5х+10=0 б) х=1

3. 7х²-14х+7=0 в) х₁=1, х₂= -2

4. 2х²-50=0 г) х₁=5, х₂= -5

2 вариант

1. 5х²+х-6=0 а) нет корней

2. 3х²+6х+3=0 б) х=1

3. х²+4х+5=0 в) х₁=1, х₂= -1

4. 3х²-48=0 г) х₁=4, х₂= -4

3 вариант

1. 2х²+7х-9=0 а) х₁=5, х₂= -5

2. 2х²-4х+2=0 б) х₁ =1, х₂= -4,5

3. х²-10х+30=0 в) нет корней

4. 5х²-125=0 г) х=1

ОТВЕТЫ

1 вариант 1) в

2) а

3) б

4) г

2 вариант 1) в

2) б

3) а

4) г

3 вариант 1) б

2)г

3) в

4) а

КАРТОЧКА №2

МИ 2. Реши предложенные уравнения по плану:

1 уравнение

1) раскрой скобки;

2) перенеси все члены уравнения в одну часть и приведи подобные члены;

3) реши полученное квадратное уравнение.

2 уравнение

Умножь каждый член уравнения на общий знаменатель и смотри пункты 1- 3

Предыдущего уравнения.

Сверь промежуточные результаты и ответы с напарником. В затруднительных случаях обратись за консультацией к учителю.

СО 2.

Уравнения, сводящиеся к квадратным.

1 вариант

1) (3х+4)²+ 3(х-2)=46;

2)

2 вариант

1) 2(1-1,5х)+2(х-2)²=1;

2)

3 вариант

1) (5х-3)(х+2)-(х+4)²=0;

2) .

4 вариант

1) х(11-6х)-20+(2х-5)²=0;

2)

ОТВЕТЫ.

1 вариант 2вариант 3 вариант 4 вариант

1) 1) х₁=4,5; х₂=1. 1) х₁=2; х₂=-1. 1) х₁=о,5; х₂= -5.

2) 1; -13. 2) х₁=2; х₂= 2) х₁=2; х₂=- 2) х₁=3; х₂= -

КАРТОЧКА №3

СО 3.

Вариант 1.

1. (х+1)(х-1)(х-2)-(х²+7х)(х-4)-2=2х;

2. 

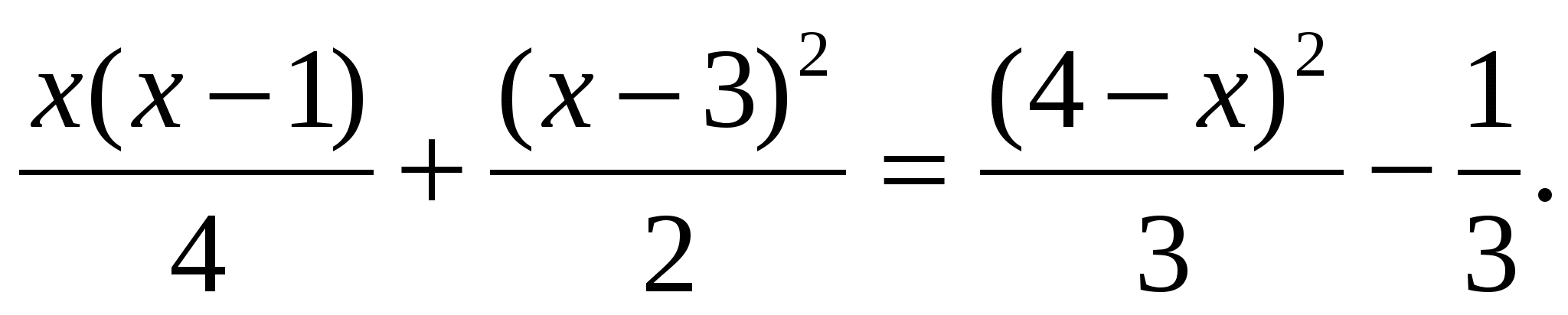
Вариант 2.

1. (х-7)(х+7)+(х-2)²=11х+30-(х+5)²;

2. 

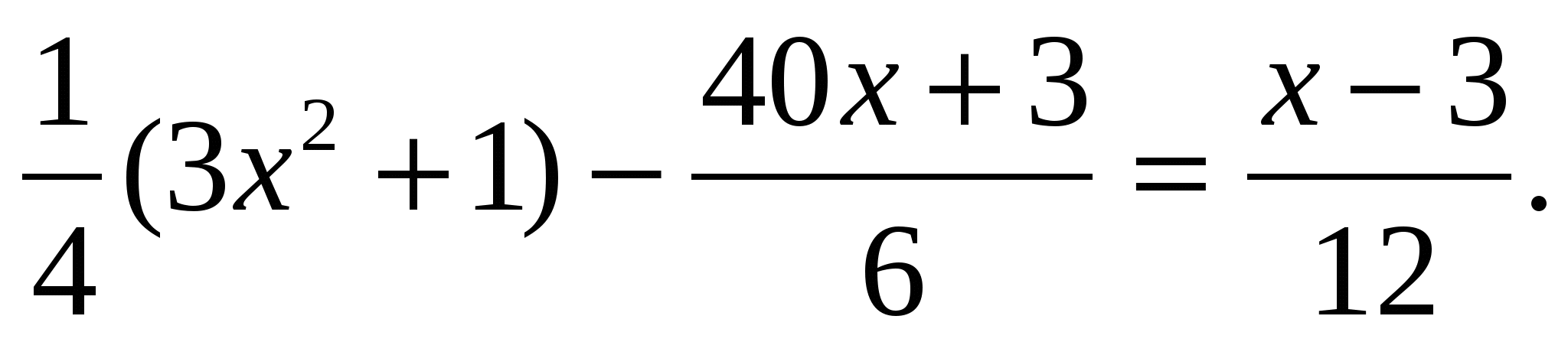
МИ 3.

Вариант 1.

Реши уравнения, сверяя промежуточные результаты и ответ

1) (х³-х-2х²+2)-(х³+7х²-4х²-28х)-2-2х=0;

х²-5х=0;

х₁=0, х₂=5.

2) 3х(х-1)+6(х²-6х+9)=4(16-8х+х²)-4;

5х²-7х-6=0;

х₁=2, х₂=

Вариант 2.

Реши уравнения, сверяя промежуточные результаты и ответ

1) х²-49+х²-4х+4=11х+30-х²-10х-25;

3х²-5х-50=0;

х₁=5, х₂=

2) 3(3х²+1)-2(40х+3)=х-3;

х²-9х=0;

х₁=0, х₂=9.

СХЕМА №1,2

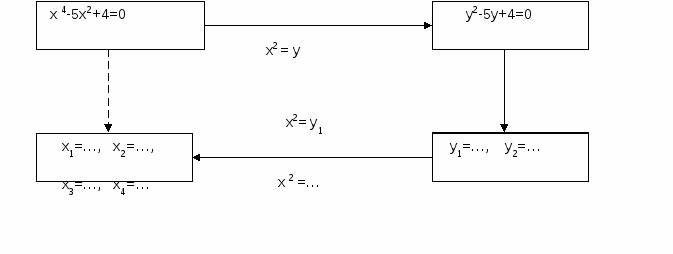
МИ 4. Заполни пропуски в схеме решения биквадратного уравнения. Ответь на предложенный вопрос и задай его напарнику. Проверьте друг у друга правильность заполнения схемы.

Вариант 1.

Сколько корней может иметь биквадратное уравнение?

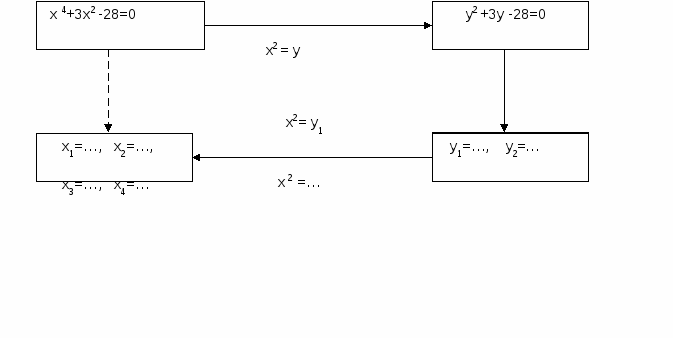
Вариант 2.

Сколько корней может иметь биквадратное уравнение?

КАРТОЧКА №4.

МИ 5.

Выполни задание, свое решение сверь с образцом на столе учителя.

СО 5.

Вариант 1.

Найди абсциссы точек пересечения графика функции у=х⁴-26х²+25 с осями координат.

Вариант 2.

Какому из указанных промежутков принадлежит сумма корней уравнения х⁴-29х²+100=0

а) (-10;-1]; б) [5;8]; в) (2;5); г) [0;1)?

КАРТОЧКА №5.

МИ 6.

К предложенному заданию даны 4 ответа, из которых только один верный. Выполни задания и запиши номер верного на твой взгляд ответа. Сверь с ключом на обратной стороне карточки.

СО 6.

Вариант 1.

Вариант 2.

Сократи дробь .

Сократи дробь

1.

1.

2.

2.

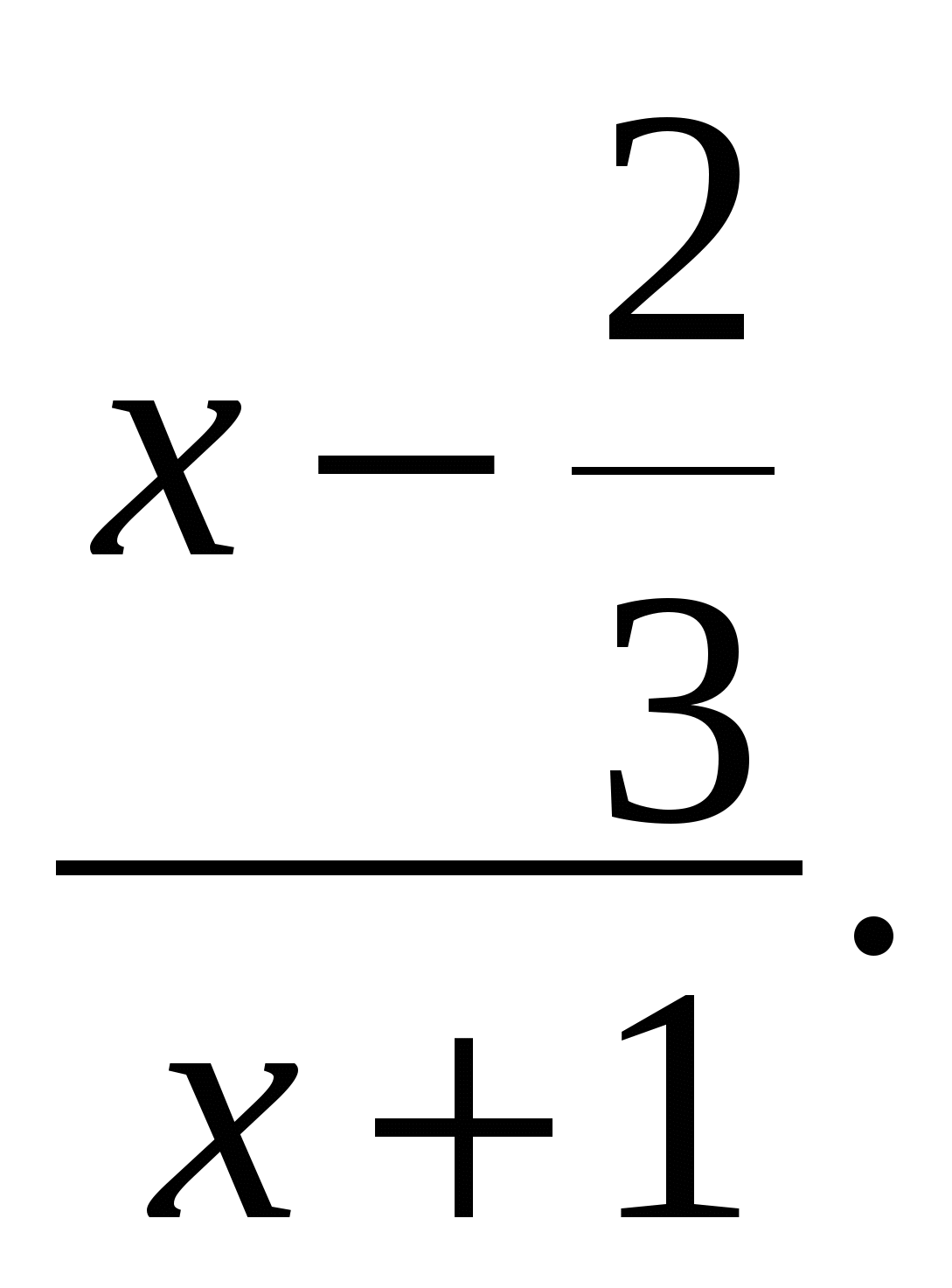
3.

3.

4.

4.

Ответы.

Вариант 1. 4.

Вариант 2. 4.

КАРТОЧКА №6.

МИ 7.

Вспомни и запиши теорему Виета. Заполни ячейки таблицы и пропуски в уравнениях. Правильность выполнения сверь с образцом на столе учителя.

Вариант 1. СО 7.

Уравнение

Сумма корней

Произведение корней

х ²-14х+6=0

х²+_х-2=0

5

х ²+21х+_=0

-6

х²+_х+_=0

-10

1

Вариант 2.

Уравнение

Сумма корней

Произведение корней

х²-5х+6=0

х²-3х+_=0

2

х²+_х+1=0

-3

х²+_х+_=0

5

-7

СО7.

МИ 7.

Вариант 3.

Вспомни и запиши теорему Виета. Отметь уравнения, корнями которых являются числа

3 и -2.

1. х²+х-6=0

2. х²- х-6=0

3. х²+х+6=0

4. х²-х+6=0

Вариант 3.

Вспомни и запиши теорему Виета. Отметь уравнения, корнями которых являются числа

4 и -5.

1. х ²-х-20=0

2. х²+х-20=0

3. х²-х+20=0

4. х²+х+20=0

КАРТОЧКА №7

МИ 8.

Используя теорему Виета выполни задание. Свое решение обсуди с консультантом.

СО 8.

Вариант 1.

Не решая уравнения х²-8х+2=0, проверить равенства (где а и в корни данного уравнения). Выбери правильное и исправь ошибочное.

1) 2) а²+в²=-60.

Вариант 2.

Не решая уравнения х²+9х-3=0, проверить равенства (где а и в корни данного уравнения). Выбери правильное и исправь ошибочное.

1) 2) а²+в²+75.

ТЕКСТ №1.

МИ 9.

Проработай текстовую задачу в паре: задайте поочередно вопросы друг другу и выполните задание, сверив ответы.

СО 9.

Периметр прямоугольника равен 10см. Найти его стороны, если известно, что площадь прямоугольника равна 24 см².

1) Для решения этой задачи составлено уравнение х(10-х)=24

Ответь на вопросы:

• Что приняли за х?

• Что выражается разностью 10-х?

• Что выражается произведением х(10-х)?

2) Составь и реши уравнение по условию задачи, запиши ответ.

КАРТОЧКА №10

МИ 10.

Открой учебник «Математика, 8 класс» под ред. Г.В. Дорофеева на стр. 140.Найди №454. Решение сверь с решебником учителя.

КАРТОЧКА №8.

МИ 11.

Выполни задание и свое решение расскажи консультанту.

СО 11.

Вариант 1.

Один из корней уравнения х²-9х-к=0 равен 4. Найди и отметь второй корень х и значение к.

• х = -5; к = -20;

• х =5; к =20;

• х =5; к =-20

Вариант 2.

Один из корней уравнения х²-7х+к=0 равен 3. Найди и отметь второй корень х и значение к.

• х =-4; к = -12;

• х =4; к =12;

• х =4; к =-12

Вариант3.

При каких значениях к уравнение 4х²+2х-к =0 имеет единственный корень?

Вариант 4.

При каких значениях с уравнение 3х²-4х+с=0 имеет единственный корень?

КАРТОЧКА №9.

МИ 12.

Уравнения с параметром. Решить уравнение с параметром означает следующее:

1. исследовать при каких значениях параметра уравнение имеет корни и сколько их при разных значениях параметра;

2. найти все выражения для корней и указать для каждого из них те значения параметра, при которых это выражение действительно определяет корень уравнения.

Ответ к задаче должен выглядеть следующим образом: уравнение при таких-то значениях параметра имеет корни …, при таких-то значениях параметра корни …, при остальных значениях параметра уравнение корней не имеет.

При затруднениях обратись за консультацией к учителю. Проверь свое решение с решебником учителя.

СО 12.

Вариант 1.

Решить уравнение с параметром (а-2)х²+2ах+а+1=0.

Вариант 2.

Решить уравнение с параметром (3+ а)х²-2х-(3-а)=0.

КАРТОЧКА №10.

МИ 13. Реши уравнение способом введения новой переменной и выполни задание. Из предложенных ответов выбери номер верного на твой взгляд ответа и сверь у консультанта.

СО 13.

Вариант 1.

При каких значениях х, принадлежащих числовому промежутку [-1; 2), верно равенство (х²+5)²-15│ х²+5│+54=0

1) 2) 3) 4 )

Вариант 1.

При каких значениях х, принадлежащих числовому промежутку [-4; 3), верно равенство

(х²-5)²-15(х²_-5)+44=0?

1) 2) 3) 4) таких значений нет.

Вариант 1.

Найдите произведение корней уравнения (х²-3х)2-2(х²-3х)-8=0.

1) -8; 2) 2; 3) -6; 4) 10.

КАРТОЧКА №14.

МИ 14. Реши уравнение, сводящееся к квадратному, способом замены переменной. Если ты забыл, как решаются такие уравнения, то

1. открой «Пособие для интенсивной подготовки к экзамену по математике», автор Рурукин А.Н. на стр.55, рассмотри решение аналогичного уравнения (пример 27). Если возникли вопросы, обратись к учителю.

2. Открой книгу Д.Т. П исьменный «Готовимся к экзамену по математике» на стр.98, рассмотри решение аналогичного уравнения. Если возникли вопросы, обратись к учителю.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ.

 

1.   Алгебра. Учебник для 8 класса. Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др, Москва, Просвещение, 2008

2.   Алгебра. Учебник для 9 класса. Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др, Москва, Просвещение, 2009

3. Математика, 8 класс под ред. Г.В. Дорофеева