Государственное автономное образовательное учреждение

Дополнительного профессионального образования

«Институт развития образования Республики Татарстан»

Структурное подразделение

Проектная работа

Методика подготовки учащихся к решению задач по темам «Задачи на движение» и «Задачи на смеси и сплавы», включенных в ЕГЭ по математике.

Выполнила :

Евстафьева Людмила Владимировна

Слушатель курсов повышения

квалификации учителей

по проблеме:

«Состояние преподавания математики в школе. Результаты ЕГЭ. Проектирование урока математики на основе требований современных

педагогических технологий»

Должность: учитель

Место работы: МОУ СОШ 161

Советского района города Казани

г. Казань - 2011г.

Содержание

1. Введение…………………………………………………………………….3

2. Алгоритмизация текстовых задач на движение и на смеси (сплавы)

как один из методов обучения учащихся решению текстовых задач……..6

3. Задачи на движение………………………………………………………..13

4. Задачи на смеси (сплавы)………………………………………………….16

4.1 Теоретические основы решения задач «на смеси, сплавы, растворы»……………………………………………………………………..16

4.2. Различные способы решения задач…….….…………………….….18

4.3 Задачи на понижение концентрации…………………………….…..20

4.4 Задачи на высушивание…………………………………….………...21

4.5 Задачи на смешивание растворов разных концентраций…..………22

4.6 Задачи на повышение концентрации…………….…………………..23

5. Задачи вариантов ЕГЭ……………………………………………………..24

5.1 Задачи на движение…………………………………………………...24

5.2 Задачи на смеси (сплавы)……………………………………………..29

5.3 Задачи,взятые из различных пробных, репетиционных, диагностических и тренировочных работ 2010-2011 гг…………………….31 6. Заключение……...……..……………………………………………………33

7. Литература…………………………………..……………………………...34

Введение

«Развивающему обществу нужны современные образованные, нравственные, предприимчивые люди, которые могут самостоятельно принимать ответственные решения в ситуации выбора, прогнозируя их возможные последствия, способные к сотрудничеству, отличающиеся мобильностью, динамизмом, конструктивностью, обладающие развитым чувством ответственности за судьбу страны» (Концепция модернизации российского образования).

Доминирующей идеей федерального компонента государственного образовательного стандарта по математике является интенсивное развитие логического мышления, пространственного воображения, алгоритмической культуры, критического мышления, овладения математическими знаниями и умениями на всех ступенях обучения, использование приобретенных знаний и умений в практической деятельности.

Компетентностный подход к образовательным результатам повлёк за собой изменения структуры и содержания независимой государственной экспертизы. Очень большой блок заданий связан с решением текстовых задач. В школьном курсе математики этот раздел не рассматривается единой темой, и у учащихся нет целостного представления о методах и способах их решения. Необходимость рассмотрения техники решения текстовых задач обусловлена тем, что умение решать задачу является высшим этапом в познании математики и развитии учащихся. Решение задач способствует развитию логического и образного мышления, повышает эффективность обучения математике и смежным  дисциплинам.

Актуальность темы: «Методика подготовки учащихся к решению задач по темам «Задачи на движение» и «Задачи на смеси и сплавы», включенных в ЕГЭ по математике» в настоящее время объясняется в необходимости систематизации материала по этому разделу. Потому что с помощью текстовой задачи формируются важные общеучебные умения, связанные с анализом текста, выделением главного в условии, составлением плана решения, проверкой полученного результата .  В ходе решения текстовой задачи формируется умение переводить ее условие на математический язык уравнений, неравенств, их систем, графических образов, т.е. составлять математическую модель.

Цель проекта:

• способствовать интеллектуальному развитию учащихся, формированию качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, развивать умение анализировать задачные ситуации, строить для общей социальной ориентации и решения практических проблем.

Задачи проекта:

• воспитывать логическую и эстетическую культуру, создавая благоприятный эмоциональный фон обучения, вызывая интерес к процессу поиска решения задач и к самому учебному предмету-математике.

• обогащать опыт мыслительной, культурно-исторической деятельности ученика, используя разнообразные исторические и современные задачи.

• раскрытие внутренних ресурсов личности ученика, выявление заложенных способностей

• снятие психологических барьеров и ограничений

• помочь ученику оценить свой потенциал с точки зрения образовательной перспективы.

Методы исследования: анализ и классификация типов текстовых задач, методической и учебной литературы,

Предполагаемые продукты

• Типология задач и методы их решения.

• Разработка методики решения текстовых задач, используемых в ГИА и ЕГЭ.

Конечный результат: успешная сдача ГИА и ЕГЭ

2. Алгоритмизация текстовых задач на движение и на смеси (сплавы)как один из методов обучения учащихся решению текстовых задач.

В школьном курсе математики решение текстовых задач считается одним из самых сложных для восприятия и усвоения учащимися разделов. Это объясняется в значительной степени тем, что если задачи другого рода требуют от своего решения формально-технического аппарата, применение которого алгоритмизировано, то решение текстовых сюжетных задач требует от учащихся еще и этапа составления уравнения или системы уравнений, понимания имеющихся в задаче условий и перевода их на математический язык; и этот этап в большей степени, чем все остальные носит эвристический характер. Чтобы облегчить данную работу следует рассматривать любую текстовую задачу как систему, в независимости от того, является ли она задачей на движение, на работу, на смеси или сплавы, на проценты и т.д.

Итак, для того, чтобы рассматривать задачу как систему, нам необходимо определить:

– элементы задачи;
– характер взаимосвязей между элементами.

Первый набор элементов, который необходимо определить в задаче как системе – это участники контекста задачи (машина и велосипед, поезда, амфибии и самолеты; рабочие и землеройки, станки и роботы; сплавы цинка и меди, раствор соли и спирта и т. д.)

Действие, производимое участником или с участником, в свою очередь также является системой. Эти действия определяются следующими элементами, которые называются компонентами:

– скорость V, время t, путь S – движения;
– производительность T, время t, объем работы V – работы;
– объем смеси V⁰, объем вещества в смеси V^в, объемная концентрация вещества в смеси cв, процентная, объемная концентрация вещества в смеси p^в% – смеси, сплава, раствора... ;
– и т.д.

По условиям задачи происходят различные изменения в значениях компонентов участников или накладываются на них какие-либо ограничения: увеличилась или уменьшилась скорость движения, известно время до встречи; вначале работали вместе, затем увеличилась производительность труда и т. д. Каждое такое изменение характеризует свою систему, состоящую из участников и соответствующих значений компонент. Назовем эти системы состояниями.

Тогда общую систему задачи можно представить в виде:

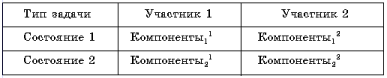
Структура системы определяется характером взаимосвязи между элементами. Таким образом, для полного раскрытия системы задачи нам необходимо определить взаимосвязи:

1. Между компонентами каждого участника в каждом состоянии.
Назовем их вертикальными взаимосвязями. Почему именно так, будет видно из ниже рассматриваемых задач.
2. Между компонентами участников в каждом состоянии.
Назовем их горизонтальными взаимосвязями или уравнивающими.
3. Между компонентами каждого участника в различных состояниях.
4. Между компонентами участников в различных состояниях.

Необходимость поиска взаимосвязи между компонентами участников в каждом состоянии требует ввести еще один элемент в систему задачи. Назовем его взаимосвязь (или общее).

Теперь наша таблица системы задачи будет выглядеть следующим образом:

В зависимости от типа задачи таблица, описывающая ее систему, примет соответствующий вид. Например, для задачи на движение:

Движение каждого участника описывает три компоненты. Для того, чтобы найти взаимосвязь между ними, нам необходимо знать значения двух компонент. В традиционном подходе к решению текстовых задач для реализации этого положения вводятся неизвестные величины – x, y и т. д. Мы используем следующий подход. Пусть, например, S₂¹ и S₂² (указываем какие-либо из компонент) как будто бы известны и дальше работаем над задачей, исходя из этого.

Рассмотрим применение предлагаемого метода анализа и решения текстовых задач на конкретных примерах.

Задачи на движение

Задача 1. Между домами Кролика и Лиса существовала прекрасная дорога в 50 км. Как-то так случилось, что они одновременно пошли друг к другу в гости. Они не пошли, а побежали. Через 5 часов, увлеченные воображаемым приятным времяпрепровождением в гостях, они пробежали мимо друг друга, рассеянно сказав: «Привет». Кролик, задумавшись над тем, неуловимо знакомым только что промелькнувшим мимо него, снизил свою скорость на 1 км/ч. Лис, почуяв что-то из того, что ему грезилось, увеличил скорость на 1 км/ч. Каково же было их разочарование, когда они не застали друг друга дома. У Лиса это разочарование наступило на 2 часа позже, чем у Кролика. С какой скоростью двигался Кролик?

Первым шагом анализа системы задачи мы определяем участников движения. Читаем текст задачи.

1. Сколько участников? – Два (Кролик и Лис).
Вторым шагом определяем состояния: сколько их и какие они.
2. Сколько состояний? – Два (до встречи, после встречи).
Третьим шагом изложим в таблице данные, необходимые для дальнейшего анализа системы задачи.

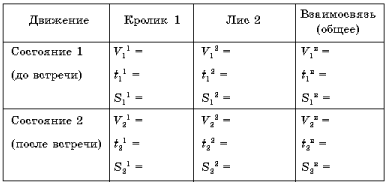
После построения таблицы еще раз читаем текст задачи (четвертый шаг) и заносим в нее данные значения компонентов.

Для удобства вашего восприятия при анализе этой задачи будем переходить от одной таблицы к другой, хотя в обычной ситуации весь анализ производится с помощью одной таблицы.

Для того, чтобы проанализировать первое состояние, нам необходимо ввести значения компонент, которые мы как бы знаем. Пусть это будет скорость кролика – V₁. Тогда имеем (в скобках цифрами мы проставляем последовательность наших рассуждений):

(4) и (5) получены из анализа взаимосвязи компонентов каждого участника в различных состояниях и условия задачи. (6) и (7) – из анализа взаимосвязи компонентов участников в различных состояниях. (8) и (9) – из анализа взаимосвязи компонентов каждого участника в состоянии 2. (10) – из условия задачи.

На основании (10) имеем уравнение

решив которое получаем: V₁ = 6 км/ч.

Ответ: 6 км/ч.

Можно отметить, что уравнения формируются из взаимосвязей между компонентами участников в состоянии. Поэтому мы и назвали их горизонтальными или уравнивающими.

На учащихся производит большое впечатление, если они понимают, что для анализа системы задачи нет особой разницы в том, какой или какие значения компонентов принять за как бы известные величины. Еще больше их интригует возможность по полностью восстановленной системе задачи составлять свои задачи, переходить от одной задачи к другой.

Рассмотрим теперь задачу на работу, произведя анализ в одной таблице, нумеруя последовательность рассуждений цифрами в скобках.

Задача 2. Два тролля раскопают спрятанные в горе сокровища за 12 дней, работая вместе. Если же они будут работать по принципу: ты сделай половину, а потом я сделаю свою половину, то им потребуется 25 дней. Сколько дней потребуется каждому из них, чтобы в одиночку добраться до сокровищ?

(1) Сколько участников работы? – Два.
(2) Сколько возможных состояний в работе? – Три: а) совместная (параллельная) работа; б) поровну произведенная работа (последовательная работа); в) каждый сам за себя (индивидуальная работа).
(3) Значения величин, которые как будто бы даны T₁ и T₂.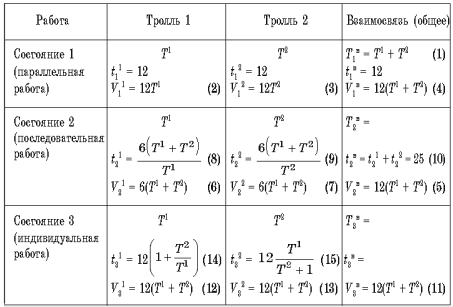

Из рассуждения (10) с учетом (14) и (15) имеем:

Пусть тогда

 

Таким образом,

Ответ: 20, 30.

Рассмотрим задачу на сплавы и смеси.

Задача 3. Алиса, будучи в Зазеркалье, нашла две плошки смеси божьего дара с яичницей. Одна из них содержала a% божьего дара, а вторая – b%. В каком отношении Алиса должна взять эти смеси, чтобы при перемешивании получить новую смесь с массовым процентным содержанием божьего дара в g%?

Так как нас будет интересовать божий дар, то мы обозначим его – бд.

1. Сколько участников (сколько смесей участвует в задаче их названия)? – Три: смесь – 1, смесь – 2, новая смесь – 3.
2. Сколько состояний? – Одно.
3. Компоненты значения, которых как бы известны – масса первой m₁⁰ и второй m₂⁰ смеси, взятые для получения смеси с массовым процентным содержанием божьего дара в g%.

Из (10), (9), (11) имеем:

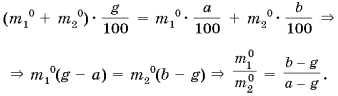
Таким образом, на рассмотренных задачах видно как использовать метод анализа системы задачи, строить уравнения, которые приводят к решению текстовых задач.

Необходимо отметить, что данная методика обучения расширяет возможности учителя по развитию творческого мышления учащихся, позволяет развивать у них целостное и системное понимание математических закономерностей и взаимосвязей.

3. Задачи на движение.
1.Движение тел по течению и против течения реки. 2.Равномерное и равноускоренное движения тел по прямой линии в одном направлении и навстречу друг другу. 3.Движение тел по окружности в одном направлении и навстречу друг другу. При решении задач на движение следует знать формулы зависимости расстояния, пройденного телом, от скорости, ускорения и времени в различных видах движения. Уметь построить графики движения в прямоугольной системе координат и прочитать графики движения, применить их для решения текстовых задач. Обратить внимание на особенности выбора переменных .Большое значение имеет правильное составление таблицы данных задачи на движение.

При решении этих задач принимать следующие допущения и правила:

1) Если нет специальных оговорок, то движение считать равномерным.

2) Скорость считать величиной положительной.

3) Повороты движущихся тел, переходы на новый режим движения

считать происходящими мгновенно.

4) Все данные сразу переводить в одни и те же единицы измерения.

Задача 1. На 60 км пути велосипедист тратит на 4 ч больше времени, чем мотоциклист. Если же он увеличит скорость на 3 км/ч, то он на тот же путь потратит в 4 раза больше времени, чем мотоциклист. Найдите скорость велосипедиста.

Анализ. Данная задача описывает движение двух объектов: велосипедиста и мотоциклиста. Вспомним, что равномерное прямолинейное движение задается формулой S = V • t , где S - путь, V - скорость, t - время, взятые в соответствующих единицах. Имеет смысл составить два уравнения.

Решение: Пусть х км/ч - скорость велосипедиста, у км/ч - скорость мотоциклиста. Тогда — 60/x - время велосипедиста, и —60 /у - время у мотоциклиста, соответствующие первой части условия.

В предполагаемом варианте скорость велосипедиста будет (х+3) км/ч и
его время 60: (x+3)ч. Получим 60 : (х+3)=4·( 60/у)

Рассмотрим систему уравнений.

Заметим, что в задаче спрашивается скорость велосипедиста, поэтому можно перейти к уравнению относительно х :

Решаем II уравнение: 60 : (х + 3) = 4 · (60 : х – 4)

15 : (х + 3) = 60 : х – 4

4х² -33х-180=0

х_I =12

х₂ = - не удовл.. условию задачи.

Ответ: 12 км/ч.

Во время экзамена за неимением времени можем использовать таблицы, в которые заносятся данные величины, а также выражения, возникающие по ходу рассуждений.

Субъект

Скорость

Время

Путь

км/ ч

T ,ч

S, км

Фактический

велосипедист

X

60/х

60

60/х-60/у=4

мотоциклист

у

60/у

60

велосипедист

х+3

60/ (x+3)

60

Предполагаем.ыйый

60 / (х+3) = 4( 60/у)

мотоциклист

мотоциклист

у

60/у

60

Задача 2. Из пункта А в пункт В выехал автобус со скоростью 40 км/ч. После того, как автобус проехал 30 км, из пункта А со скоростью 60 км/ч

выехал автомобиль, который прибыл в пункт В на ч позже автобуса. Найдите расстояние между пунктами.

Решение: Совместное движение началось в момент выхода автомобиля из пункта А. К этому времени автобус прошел 30 км со скоростью 40 км/ч за

- это 1 участок пути автобуса.

Второй участок пути автобус прошел за t ч. Так как скорость движения 40 км/ч, то это расстояние равно 40t км, а в общей сложности автобус прошел (30 + 40 t) км . За t часов автомобиль со скоростью 60 км/ч прошел 60 t км и до пункта В ему осталось пройти 60. Таким образом, расстояние от пункта

А до пункта В равно (60t + 5) км. Составим уравнение:

30 + 40 t = 60 t+5, откуда t = . Тогда расстояние между пунктами равно 30+(км)

Ответ:

4. Задачи на смеси (сплавы).

4.1.Теоретические основы решения задач «на смеси, сплавы, растворы»

Задачи на смеси и сплавы имеют практическое значение, являются хорошим средством развития мышления учащихся. Они расширяют базовый курс математики и позволяют учащимся осознать практическую ценность математики. Задачи на растворы, смеси и сплавы обладают диагностической и прогностической ценностью, то есть с их помощью можно проверить знания основных разделов школьной математики, уровень математического и логического мышления, первоначальные навыки исследовательской деятельности, то есть лишний раз проверить и оценить свои способности к математике. При решении задач на растворы, смеси и сплавы очевидны межпредметные связи с химией, физикой и экономикой, знание этого повышает учебную мотивацию учащихся по всем предметам.

Трудности при решении этих задач могут возникнуть на различных этапах:

• составления математической модели ( уравнения, системы уравнений, неравенства)

• решения полученной модели;

• анализа математической модели ( по причине кажущейся ее неполноты: не хватает уравнений в системе или слишком много неизвестных и пр.)

Тип задач на составление уравнений и систем уравнений – задачи на сплавы и смеси, решение которых связано с понятиями «концентрация», «процентное содержание», «проба», «влажность».

При решении задач данного типа использу­ются следующие допущения:

1. Всегда выполняется «Закон сохранения объема или массы»:
если два раствора (сплава) соединяют в «новый» раствор (сплав),
то выполняются равенства:

V = V₁ + V₂ - сохраняется объем;

т =m₁+ т₂~ закон сохранения массы.

2. Данный закон выполняется и для отдельных составляющих частей

(компонентов) сплава (раствора).

3. При соединении растворов и сплавов не учитываются хими­ческие взаимодействия их отдельных компонентов.

Концентрация - это число, показывающее, сколько процентов от всей смеси составляет растворимое вещество. Если масса смеси т кг, масса растворимого вещества а кг, концентрация р %, то между этими величинами существует следующая зависимость: ; 100*а = т*р.

Пример работы над задачами с понятием концентрации:

Масса смеси

т ( кг)

Масса растворимого вещества

а ( кг)

Концентрация р %

10

1

= 10%

5

2

= 0,4 = 40%

4

0,5

0,5:4 =0,125=12,5%

m_c

т_в

т_в / m_c = к

После получения этой формулы задачи на растворы будут осознанно решаться учащимися на основе соотношения:

т_в =k*m_c; m_c = т_в:к; .

Процентное содержание вещества в растворе, иногда называют %-м раствором, например, 15%-й раствор соли.

4.2 Различные способы решения задач

Одну и ту же задачу можно использовать в 5-м или 6-м классе при изучении темы, а потом ее включить при повторении в 9-м или 11-м классе. В процессе решения задач учащиеся повторяют как найти часть от числа и число по его части, прямую и обратную пропорциональные зависимости, способы решения уравнений и другое.

1. Сколько нужно взяты 10%-го и 30%-го растворов марганцовки, чтобы получить 200 г 16%-го раствора марганцовки?

Решение. Способ I. (5 класс) Пусть масса первого раствора — х г. Заполним таблицу по условию задачи:

марганцовка

раствор(г)

марганцовка(г)

1-й раствор

10 % или 0,1

Х

0,1х

2-й раствор

30% или 0,3

200-х

0,3(200-х)

3-й раствор

16 % или 0,16

200

0,16*200

Составим и решим уравнение: 0,Iх + 0,3(200 — х) = 0,16 *200, 0,2х = 28, откуда

х = 140.

Ответ: 140 г 10%-го и 60 г 30%-го.

Способ II. (7 класс) Пусть масса первого раствора — х г, а масса второго раствора — у г. Заполним таблицу по условию задачи:

марганцовка

раствор (г)

марганцовка(г)

1-й раствор

10 % или 0,1

Х

0,1х

2-й раствор

30% или 0,3

y

0,3y

3-й раствор

16 % или 0,16

200

0,16*200=32

Составим и решим систему уравнений:

х+у=200, х=200—у, х=140,

0,1х+0,3у=32; 0,1(200—у)+0,зу=32; у=б0.

Ответ: 140 г 10%-го и 60 г 30%-го.

Способ III. Решим эту задачу старинным способом по правилу

«креста».

Составим схему:

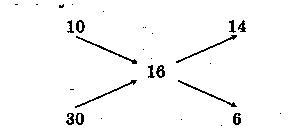
В левой колонке схемы записаны процентные содержания марганцовки в имеющихся растворах. Посередине — процентное содержание марганцовки в полученной смеси. В правой — разности процентных содержаний имеющихся растворов и полученной смеси (вычитаем из большего числа меньшее и записываем разность на ту диагональ, где находятся, соответственно, уменьшаемое и вычитаемое).

Исходя из схемы делаем вывод: в 200 г смеси содержится 14 частей 10%-го раствора и 6 частей 30%-го раствора. Найдем их массы:

200:(14+6)14=140г; 200 : (14 + 6) .6 = 60 г.

Ответ: 140 г 10%-го и 60 г 30%-го.

В старших классах можно показать, как выводится правило «креста». Пусть смешали два раствора: первый — массой m₁ г и концентрацией a₁ и второй — массой m₂ г и концентрацией а₂, получили раствор массой (m₁ + m₂) г и концентрацией а, причем а₁ < а₃ < а₂.

Найдем зависимость масс исходных растворов от их концентраций.

Масса основного вещества в первом растворе равна a₁m₁, во втором растворе —, а₂ m₂г, а в смеси a₃ (m₁ + m₂) г.

Составим равенство a₁m₁+ а₂m₂ = a₃(m₁ + m₂) и из него получим:

a₁m₁ - а₃ m₁ = a₃m₂ - а₂m₂

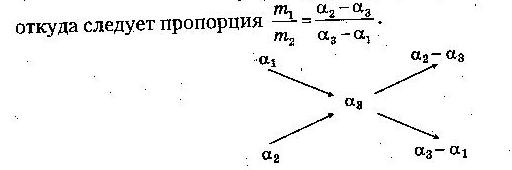
4.3 Задачи на понижение концентрации

1.(5 класс) Сироп содержит 18% сахара. Сколько килограммов воды нужно добавить к 40 кг сиропа, чтобы содержание сахара составило 15%?

Решение. Пусть надо добавить х кг воды. Заполним таблицу по условию задачи.

сахар

Сироп(раствор)(г)

сахар(г)

Было

18% или 0,18

40

0,18*40=7,2

стало

15% или 0,15

40+х

0,15*(40+х)

Так как масса сахара не изменилась, то составим и решим уравнение:

0,15(40 + х) = 7,2, О,15х = 1,2, откуда х = 8.

Ответ: 8 кг

2. (6 класс) Сколько килограммов 5%-го раствора соли надо добавить к 15 кг 10%-го раствора той же соли, чтобы получить ее 8%-ный раствор?

Решение. Пусть добавили х кг 5%-го раствора соли. Заполним таблицу по условию задачи:

Раствор

Соль(%)

раствор(кг)

соль(кг)

10%-ный

10%или 0,1

15

0,1*15=1,5

5%-ный

5% или 0,05

Х

0,05х

8%-ный

8% или 0,08

15+х

1,5+0,05х

Составим и решим уравнение: 1,5 + 0,05х = 0,08 (15 + х), 0,ОЗх= 0,3,

откуда х= 10.

Ответ: 10 кг.

4.4 Задачи на «высушивание»

При решении этих задач надо объяснить учащимся , что все тела, вещества, продукты содержат в себе воду, которая частично испаряется. Поэтому при решении этих задач мы каждый раз разделяем данное нам вещество на воду и «сухой остаток», масса которого не меняется в условиях задачи.

1. (5 класс) Трава при высыхании теряет около 28% своей массы. Сколько было накошено травы, если из нее было получено 1,44 т сена?

Решение. Заполним таблицу по условию задачи:

Масса в тоннах

Содержание в %

Трава

Х

100

сено

1,44

100-28=72

Зависимость прямо пропорциональная. Составим и решим пропорцию х1,44 = 10072, откуда х = 1,44∙10072 =2 т Ответ: 2 т.

2. (6 класс) Имеется 0,5 т целлюлозной массы, содержащей 85% воды. После выпаривания получили массу, содержащую 25% целлюлозы. Сколько килограммов воды было выпарено?

Решение. Пусть выпарили х кг воды. Заполним таблицу по условию задачи:

Целлюлоза %

целлюлозная масса кг

Целлюлоза

кг

Было

100-85=15%=0,15

500

500 ∙0,15

стало

25%=0,25

500-х

(500-х) ∙ 0,25

Составим и решим уравнение: 500*0,15 = (500 — х)0,25, 0,25х = 50, откуда х = 200.

Ответ: 200 кг.

3. (6 класс) Из 60%-го водного раствора спирта испарилась половина воды и 23 спирта. Каково процентное содержание спирта в получившемся растворе?

Решение. 60%-й раствор спирта содержит 60% спирта и 100—60=40% воды. Если масса раствора была х г, то спирта в нем было 0,6х г, а воды — 0,4х г. В результате испарения в растворе осталось:

1) спирта 1- 2 3= 13, или 13 ∙ О,6х=О,2х г;

2) воды 1- 12= 12, или 12 ∙∙ 0,4х=0,2х г.

Рассчитаем концентрацию получившегося раствора:

∝=mM=0,2х0,2х+0,2х = 0,2х0,4х = 12 = 50%

Ответ: 50%.

4.5 Задачи на смешивание растворов разных концентраций

1. .(6класс) При смешивании 5%-го и 40%-го растворов кислоты получили 140 г 30%-го раствора кислоты. Сколько грамм каждого раствора было взято?

Решение. Пусть взяли х г 5%-го раствора кислоты. Заполним таблицу по условию задачи:

Кислота %

Раствор( г)

Кислота( г)

5%-ный

0,05

Х

0,05х

40%-ный

0,4

140-х

0,4 (140-х)

смесь

0,3

140

0,3 ∙ 140=42

Составим и решим уравнение:

0,05х + 0,4(140 — х) =42, 0,35х = 14, х = 40.

Ответ: 40 г 5%-го и 100 г 40%-го.

4.6 Задачи на повышение концентрации

1. (6 класс) Сплав массой 36 кг содержит 45% меди. Сколько меди нужно добавить, чтобы новый сплав содержал 60% меди?

Решение. 45% — это 0,45, 360,45 = 16,2 кг меди содержится в данном сплаве.

Пусть масса меди, которую надо добавить в сплав, равна х кг, тогда (36 + х) кг — масса сплава после добавления меди, а масса меди в новом сплаве (16,2 + +х) кг. Зная, что медь в новом сплаве составила 60%, составим и решим уравнение: 16,2 + х = (36 + х) Х Х 0,6, 0,4х= 5,4, откуда х = 13,5.

Ответ: 13,5 кг.

2. (8 класс) В сплаве олова и меди содержалось 11 кг меди. После того как в сплав добавили 7,5 кг олова, концентрация олова повысилось на 33%. Какова первоначальная масса сплава?

Решение. Пусть первоначальная масса сплава х кг, в нем содержалось 11 кг меди и (х —11) кг олова. Заполним таблицу по условию задачи:

Сплав( кг)

Олово( кг)

Олово( %)

Было

Х

Х-11

х-11х ∙ 100

стало

Х+7,5

Х-11+7,5=х-3,5

х-3,5х+7,5 ∙ 100

Составим и решим уравнение:

х-3,5х+7,5 ∙ 100 – х-11х ∙ 100 = 33

IООх (х — 3,5) — 100(х + 7,5)(х — 11) = ЗЗх (х + 7,5),

22х²+165х—5500=0. D =27225+484000=511 225.

Х_{1,2 =-165±71544}; х₁ = -165+17544 = 12,5;

Х₂ <0, что не удовлетворяет условию задачи (х >0). Значит, первоначальная масса сплава 12,5 кг.

Ответ: 12,5 кг.

5. Задачи вариантов ЕГЭ.

5.1. Задачи на движение.

Решение задания B12 №40117

Пристани A и B расположены на озере, расстояние между ними 288 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 7 км/ч больше прежней, сделав по пути остановку на 14 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.

Решение:
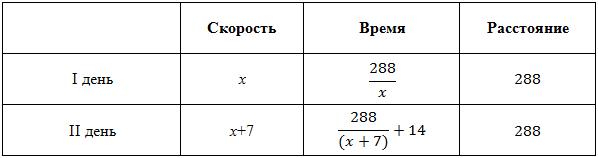
Пусть скорость баржи в первый день - x. Составим таблицу для каждого дня:

Приравняем время, потраченное на дорогу в первый и во второй день, так как он затратил на обратный путь столько же времени, сколько на путь из А в В.

















х₁ не удовлетворяет условию задачи.

Ответ: 9 км/ч.

Решение задания B12 №5615

Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.

Решение:
Пусть скорость первого автомобиля - x, а расстояние между A и B примем за 1. Составим таблицу для каждого автомобилис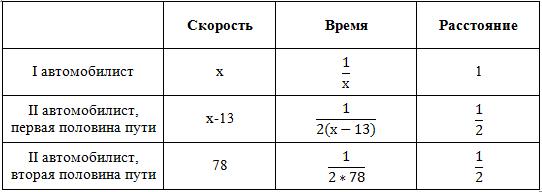та:

Приравняем время, потраченное на дорогу первым и вторым автомобилистами, так как они потратили одинаковое время.














х₁ не удовлетворяет условию задачи.

Ответ: 52 км/ч.

Решение задания B12 №5715

Моторная лодка прошла против течения реки 55 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 8 км/ч. Ответ дайте в км/ч.

Решение:
Пусть скорость течения реки - x. Составим таблицу для каждого направления: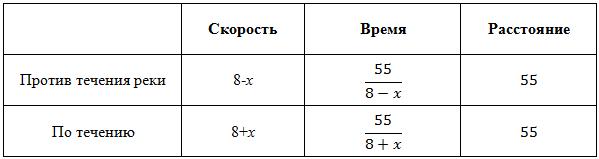

Мы знаем, что на путь по течению лодка затратила на 6 часов меньше.















х₁ не удовлетворяет условию задачи.

Ответ: 3 км/ч.

Решение задания B12 №5629

Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 108 км. На следующий день он отправился обратно со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.

Решение:

Пусть скорость велосипедиста в первый день - x. Составим таблицу для каждого дня: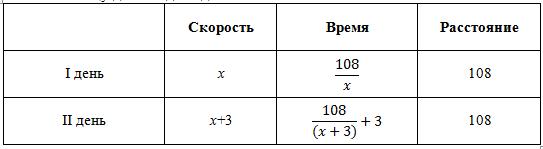

Приравняем время, потраченное на дорогу в первый и во второй день, так как он затратил на обратный путь столько же времени, сколько на путь из А в В.

х₁ не удовлетворяет условию задачи.

Ответ: 9 км/ч.

Решение задания B12 №5723

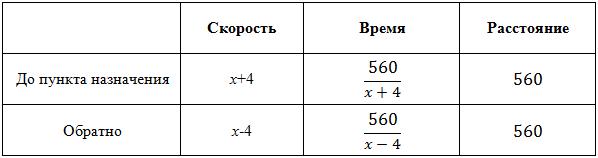
Теплоход проходит по течению реки до пункта назначения 560 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 56 часов после отплытия из него. Ответ дайте в км/ч.

Решение:
Пусть скорость теплохода - x. Составим таблицу для каждого направления:

Мы знаем, что на весь путь теплоход затратил 56 часов, включая стоянку.

х₁ не удовлетворяет условию задачи.

Ответ: 24 км/ч.

5.2 Задачи на смеси (сплавы).

№1

Смешали 30%-ный раствор соляной кислоты с 10%-ным и получили 600г 15%-ного раствора. Сколько граммов каждого раствора было взято?

Решение: 30%=0,3; 10%=0,1: 15%=0,15

600 Х 0,15=90(г) кислоты в полученной смеси

30%-ный раствор

10%-ный раствор

15%-ный раствор

Раствор(г)

Х

У

600

соляная кислота (г)

0,3Х

0,1У

90

х+у=6000,3х+0,1у=90 ; х+у=6003х+у=900

Х=150, у=600-150=450.

Ответ: 150г., 450г.

№2

Имеется кусок сплава меди с оловом массой 15 кг, содержащий 40% меди. Сколько чистого олова надо прибавить к этому куску, чтобы получившийся новый сплав содержал 30% меди?

Решение: 40%=0,4,

30%=0,3

величины

Дано

добавлено

всего

Общая масса(кг)

15

х

15+х

Процент меди

40%=0,4

0

30%=0,3

Медь в кг

15х0,4=6

0

0,3(х+15)

0,3(х+15)=6; 0,3х=6-4,5: 0,3х=1,5; х=5.

Ответ: 5кг.

№3

Сколько чистой воды нужно добавить к 100г 60%-го раствора кислоты, чтобы получить 30%-ный раствор?

Решение:

величины

Дано

добавлено

всего

Общая масса (г)

100

х

100+х

Процент кислоты

60%=0,6

0

30%=0,3

Кислота (г)

0,6х100=60

0

0,3(100+х)

0,3(100+х)=60; 30+0,3х=60; 0,3х=30; х=100

Ответ: 100г.

№4

К раствору, содержащему 40г соли, добавили 200г воды, после чего массовая доля растворенной соли уменьшилась на 10%. Сколько воды содержал раствор и какова была в нем массовая доля соли?

Решение:

величины

дано

добавлено

Всего

Общая масса (г)

х

200

Х+200

Процент соли

(40*100):х=4000/х

0

4000/(х+200)

Соль (г)

40

0

40

4000 х - 4000х(х+200)=10; 80000х(х+200)=10

Х=200 или х=-400 (не удовлетворяет условию задачи)

1. 200-40=160(г) воды; 2) 4000:200=20(%) соли.

Ответ: 160г, 20%.

№5

Первый сплав состоит из цинка и меди, входящих в него в отношении 1:2, а другой сплав содержит те же металлы в отношении 2:3. Из скольких частей обоих сплавов можно получить третий сплав, содержащий те же металлы в отношении 17:27?

Решение:

сплавы

Цинк (кг)

Медь (кг)

Возьмем для нового сплава (кг)

1 сплав

х

2х

А=3х

2 сплав

2у

3у

В=5у

Новый

Х+2у

2х+3у

Х+2у2х+3у = 1727, или 27х+54у = 34х+51у; 3у=7х, то АВ=3х5у=21х35у=9у35у=935

Ответ: сплав нужно взять в соотношении 9:35.

6. Задачи, взятые из различных пробных, репетиционных, диагностических и тренировочных работ 2010-2011 гг.

1. Смешали некоторое количество 15 процентного раствора некоторого вещества с таким же количеством 19 процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

2. Смешали 30%-вьй раствор соляной кислоты с 10%-ным и получили 6ООг 15%-го раствора Сколько граммов 1 0%-го раствора было взято?

3. Имеется два сплава. Первый содержит 5% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава меньше массы второго?

4. Имеется два сплава с разным содержанием золота. В первом сплаве содержится 35% золота, а во втором — 60%. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?

5. При смешивании первого раствора кислоты, концентрация которого 20%. и второго раствора этой ж кислоты концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый второй растворы?

6. Смешали З литра 40-процентного водного раствора некоторого вещества с 12 литрами 35-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

7. Смешали 8 литров 15-процентного водного раствора некоторого вещества с 12 литрами 40-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

8. Смешали некоторое количество 17-процентного раствора некоторого вещества со втрое большим количеством 9-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

9. Смешали некоторое количество 14-процентного раствора некоторого вещества со вдвое большим количеством 8-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Заключение

Задачи выбраны по справочникам и учебным пособиям, по экзаменационным материалам, в том числе и вариантам ЕГЭ. Собранный материал можно использовать на уроках и для самоподготовки учащихся. Для большей наглядности обучения используется разное оформление решений и заполнения таблиц.

Литература:

1.Далингер В.А. Все для обеспечения успеха на выпускных и вступительных экзаменах по математике. Вып. 2. Текстовые задачи, решаемые методом составления уравнений: Учеб. Пособие. Омск. Изд-во ОмГПУ, 1996

2.Далингер В.А. Обучение учащихся решению текстовых задач методом составления уравнений: Пособие для учителей.Омск: изд-во ОИУУ,1991

3.Ковалева Г.И. Математика. Тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов. Издание 2-е, исправленное. Волгоград. Изд-во «Учитель», 2011г.

4.Копылова Н.П. Решебник «Задачи на смеси и сплавы» 2005г. г.Шелехов.

Под редакцией Лысенко Ф.Ф. «Тематические тесты» Издательство «Легион-М»,2010

5.Мальцев Д.А., Мальцева Л.И. «Математика. Все для ЕГЭ 2011» 2010г. г.Москва

6.Прокопенко Н.И. «Задачи на смеси и сплавы» 2010г. г. Москва

7.Семенова А.Л., Ященко И.В. 3000 задач с ответами по математике. Банк заданий ЕГЭ. Издание 2-ое, стереотипное.Изд-во «Экзамен», Москва, 2011г.

8.ЕГЭ Математика 2011 г. ФИПИ-М…Интеллект-Центр,2011.-144с.

9.http://www.fipi.ru