Волгоградская государственная академия повышения квалификации и переподготовки работников образования

Кафедра теории и методики обучения математике

Тема: Обучение решению текстовых задач как средство повышения математического образования

Квалификационная работа соискателя

высшей квалификационной категории:

Полусмаковой Ирины Васильевны, учителя математики

МОУ гимназии №10 Кировского района г. Волгограда

Волгоград, 2013

В современном мире значение образования как важнейшего фактора формирования нового качества экономики и общества увеличивается вместе с ростом влияния человеческого капитала. Немаловажную роль в качественной подготовке квалифицированных специалистов играет школа, по отношению к которой предъявляется все большее число требований повышения качества знаний учащихся, улучшения их подготовки к самостоятельной жизни. Появляется потребность полноценного математического образования для каждого школьника, необходимость достижения всеми выпускниками средней школы гарантированного уровня подготовки по предмету, что поможет им в дальнейшей жизни. За последнее время отмечается, что качество математических знаний многих школьников не соответствует требованиям современной жизни.  Причины такого состояния математической подготовки школьников кроются во многом, и   как показывают наблюдения за учебным процессом, одна из наиболее значимых причин заключается в том, что многие учащиеся на каждом этапе в школе не достигают уровня подготовки по предмету, обеспечивающего дальнейшее успешное его изучение.  

К числу качеств полноценных знаний учащегося относят полноту и глубину, оперативность и гибкость, конкретность и обобщенность, систематичность и системность, осознанность и прочность. Между всеми качествами знаний имеется определенная связь. Каждое качество придает знаниям специфические черты, дополняющие друг друга. Так, на оперативность знаний влияет глубина и полнота, так как чем больше знаний и связей между ними усвоит человек, тем больше ситуаций, к которым он может эти знания применить.

Одним из средств повышения качества знаний учащихся является решение текстовых задач. С начала и до конца обучения в школе математическая задача неизменно помогает ученику правильно формировать математические понятия, глубже выяснять различные взаимосвязи в окружающей его жизни, дает возможность применять на практике изучаемые теоретические положения. В тоже время решение задач способствует развитию логического мышления, памяти и внимания школьников.

Математические задачи, в которых есть хотя бы один объект, являющийся реальным предметом, принято называть текстовыми (сюжетными, практическими). Перечисленные названия берут начало от способа записи (задача представлена в виде текста), сюжета (описываются реальные объекты, явления, события), характера математических выкладок (устанавливаются количественные отношения между значениями некоторых величин, связанные чаще всего с вычислениями). В последнее время наиболее распространённым является термин «текстовая задача» [1].

Особенности текста задачи могут определить ход мыслительного процесса при ее решении. При решении текстовых задач учащиеся выполняют различные мыслительные операции: анализ и синтез, сравнение, абстрагирование и конкретизация, обобщение, применение индукции и дедукции. Умение решать текстовые задачи является одним из основных показателей уровня математического развития, глубины усвоения учебного материала.

Текстовой задачей будем называть описание некоторой ситуации (явления, процесса) на естественном и (или) математическом языке с требованием либо дать количественную характеристику какого–то компонента этой ситуации, либо установить наличие или отсутствие некоторого отношения между её компонентами или определить вид этого отношения, либо найти последовательность требуемых действий [2].

В соответствии со структурой задачи и процессом её решения можно рассматривать следующие составляющие общего умения решать задачи [4]:

• читать текст задачи;

• выделять вопрос и условие задачи;

• оформлять краткую запись текста задачи или чертёж по тексту задачи;

• выделять данные и искомые, устанавливать связи между ними;

• переводить словесный текст задачи на математический язык;

• устанавливать полноту постановки задачи;

• актуализировать теоретические знания, необходимые для решения задачи;

• давать оценку результатам решения;

• составлять новые задачи и т.д.

Демидовой Т.Е, Тонких А.П. [1] выделены этапы организации деятельности по решению текстовых задач. Деятельность по решению задачи включает следующие этапы независимо от выбранного метода решения:

1. Анализ содержания задачи.

2. Поиск пути решения задачи и составление плана ее решения.

3. Осуществление плана решения задачи.

4. Проверка решения задачи.

Рассмотрим каждый этап решения задачи.

1. Анализ задачи.

Основное назначение этапа – осмыслить ситуацию, отражённую в задаче; выделить условия и требования, назвать данные и искомые, выделить величины и зависимости между ними (явные и неявные).

2. Поиск пути решения задачи и составление плана её решения.

Назначение этапа – завершить выделение величин, входящих в задачу, данные и искомые чисел; установление связей между данными и искомыми величинами и указать последовательность использования этих связей.

3. Осуществление плана решения задачи.

Назначение этапа – найти ответ на требование задачи по составленному ранее плану. Немаловажную роль при решении задач играет запись найденного решения. При записи именованных чисел, выраженных в метрических мерах, используются наименования, принятые в международной системе единиц.

4.Проверка решения задачи.

Назначение этапа – установить, правильно ли понята задача, и выяснить, не противоречит ли полученный ответ всем другим условиям задачи. Этот этап является обязательным при решении задач. Следует помнить, что логичные рассуждения на других этапах решения задачи не гарантируют правильности её решения.

Рассмотрим, как можно организовать деятельность учащихся по решению текстовой задачи в соответствии с указанными этапами.

Задача. По плану бригада должна была выполнить заказ за 10 дней. Но фактически она перевыполняла норму на 27 деталей в день и за 7 дней работы не только выполняла предусмотренные планом задание, но и изготовила сверх плана 54 детали. Сколько деталей в день должна была изготовить бригада по плану?

Анализ текста задачи. После прочтения текста задачи анализ может быть проведен посредством рассмотрения следующих вопросов (самими учащимися или с помощью учителя):

• За сколько дней бригада должна выполнить заказ по плану?

• За сколько дней бригада фактически выполнила заказ?

• Почему бригада выполнила заказ раньше намеченного срока?

• Сколько деталей изготовила бригада сверх плана?

• Какие величины содержатся в задаче?

• Как связаны между собой производительность труда, время и объем выполняемой работы? (Учитель может конкретизировать этот вопрос, исходя из возможностей учащихся.)

• Сколько различных ситуаций можно выделить в задаче?

• Какие величины, входящие в условие и вопрос задачи, неизвестны?

• Решалась ли раньше задача, похожая на эту?

В итоге первого этапа работы над задачей с учетом основного отношения выполняется запись текста задачи.

Величины

Ситуация

По плану

Фактически

Производительность бригады, дет. в день

?

<

?

Время работы, дн.

10

7

Объем выполненной работы, дет.

?

<

?

На 27

54

Для выяснения связи между значениями одной и той же величины перед учащимися ставятся соответствующие вопросы, например: в каком случае производительность труда бригады была выше? На сколько деталей в день перевыполняла норму?

Правильный ответ на первый вопрос позволяет поставить в таблице соответствующий знак неравенства между неизвестными значениями одноименной величины. Ответ на второй вопрос позволяет записать: «На 27» (в указанном в таблице месте). Полученная запись позволяет учащимся актуализировать часть условия задачи: производительность бригады, предусмотренная планом, на 27 деталей в день меньше фактической. Аналогично поступают при выяснении связи между неизвестными значениями другой величины. В данном случае сравнивается плановый и фактический объем выполненной работы.

Поиск способа решения задачи. На этом этапе обсуждается стратегия решения задачи. Затем вводится обозначение искомой или другой неизвестной величины в зависимости от выбранной учителем совместно с учащимися стратегии. Далее, пользуясь установленными зависимостями между значениями одноименных величин и основным отношением, реализованным в задаче (т.е. зависимостью между величинами), на основе табличной записи текста заполняется таблица поиска решения задачи:

Величины

Ситуация

По плану

Фактически

Производительность бригады, дет. в день

х

<

х+27

Время работы, дн.

10

7

Объем выполненной работы, дет.

10х

<

(х+27)•7

На 27

На 54

Исходя из модели поиска решения, выписывается неравенство 10х<(х+27)•7 на 54, с помощью которого составляется уравнение 10х+54=(х+27)•7 или уравнение 10х=(х+27)•7–54.

Осуществление плана решения задачи. Отсюда естественно вытекает план решения задачи, который включает в себя поиск решения (способ получения уравнения) и решение полученного уравнения.

Имеем уравнение: 10х+54=(х+27)•7. Решим его:

10х+54=7х+189,

3х=135,

х=45.

Данное уравнение имеет один корень – число 45.

Проверка решения задачи.

Необходимо проверить, удовлетворяет ли полученный корень уравнения условию и требованию задачи. В связи с этим необходимо сделать проверку корня уравнения по смыслу задачи.

Проверка состоит в том, что по найденному значению х по порядку вычисляются значения входящих в задачу величин. При этом проверяется, удовлетворяют ли эти величины смысловым ограничениям. Если все найденные значения величин им удовлетворяют, то корень уравнения дает решение задачи.

С этой целью пользуемся моделью поиска решения задачи. По смыслу данной задачи все входящие в нее величины должны принимать положительные значения. Проверяем, выполняется ли это для найденного значения х=45:

х=45 положительное число.

х+27=45+25=72 положительное число.

(х+27)•7=72•7=504 положительное число.

10х=10•45=450 положительное число.

504–504=54 положительное число, являющееся данным.

Следовательно, значение х=45 удовлетворяет условию задачи, т.е. является ее решением.

Ответ: бригада должна изготовить в день по плану 45 деталей.

Важным этапом формирования умения решать текстовые задачи является обучение школьников построению различных вспомогательных моделей для конкретных задач. Приведём примеры.

Пример 1. В первом бидоне краски в 2 раза больше, чем во втором. Если из первого бидона взять 2 л краски, а во второй добавить 5 л краски, то в обоих бидонах краски станет поровну. Сколько краски было в каждом бидоне первоначально?

В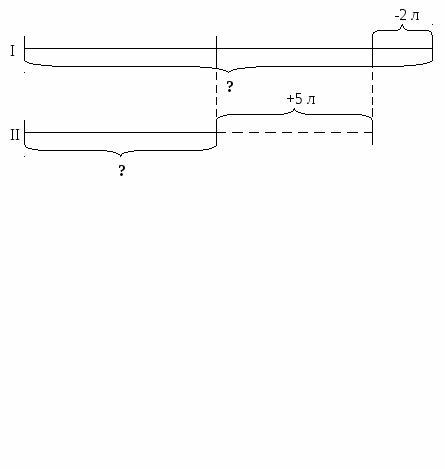спомогательная модель задачи (в виде схематического чертежа) показана на рисунке.

Пример 2. В первую неделю типография получила с фабрики шесть рулонов бумаги одного сорта и заплатила за них 204 р. Сколько рублей должна заплатить типография за месяц, если она получила 10 таких же рулонов бумаги того же сорта?

Вспомогательная модель задачи (в виде таблицы) показана на таблице.

Число рулонов(шт.)

Стоимость (р.)

Цена (р.)

6

204

Одинаковая

10

?

Пример 3. Смешали 30%–ный раствор соляной кислоты с 10%–ным и получим 600 г 15%–ного раствора. Сколько граммов каждого раствора было взято?

В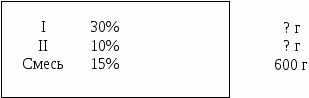спомогательная модель задачи (в виде краткой записи) показана в таблице.

Вспомогательные модели являются действенным средством поиска решения задачи и составления плана её решения.

Рассмотрим способы организации диалога с классом на примере решения задачи:

Задача. Две машины выехали одновременно из одного пункта и едут в одном направлении. Первая машина идет со скоростью 50 км/ч, а вторая – 40 км/ч. Спустя полчаса из этого же пункта и в том же направлении выехала третья машина, которая обогнала первую на полтора часа позже, чем вторую. Какова скорость третьей машины?

После прочтения условия учитель начинает диалог с классом со следующих вопросов:

1. «Какой процесс рассматривается в задаче?»

«Движение»

2. «Сколько объектов движутся и какие они?»

«В задаче речь идет о трех объектах, о машинах»

3. «Даем ли мы в математике определения этим объектам, изучаем ли их свойства?»

«Конечно, нет»

Таким образом, все вместе устанавливаем, что перед нами задача, которую, пока нельзя назвать математической. Она просто не сформулирована на математическом языке. «Что же в ней лишнее и чего не недостает для того, чтобы считать задачу математической?» На этот вопрос учащимся сразу ответить трудно и они высказывают разные точки зрения и критикуют друг друга. В конце концов, добираются до вывода, что математике все равно какие именно объекты движутся, их можно даже не называть, отличая, допустим, только по номерам (объект №1, объект №2 и объект №3). Математический язык начинается тогда, когда появляются уравнения, связывающие величины, о которых идет речь. Так созревает следующий вопрос учителя:

–– Так, о каких величинах мы должны говорить, решая задачу на движение?

–– Мы должны говорить о времени движения, скорости движения и о пути, пройденном с одной и той же скоростью».

–– Давайте попробуем увидеть, сколько же значений принимают эти три величины.

Ребята пытаются ответить: «Сначала два объекта одновременно выезжают в одном направлении, а вот потом...»

Здесь учитель прерывает учащихся и просит их обратить внимание на то, что они самым естественным образом разделили условие задачи на две части, говоря про «сначала» и про «потом». Эти две части будем называть ситуациями.

Диалог продолжается:

–– Так сколько же ситуаций описано в задаче?

–– Две

–– Каковы же эти ситуации?

–– Спустя полчаса из этого же пункта и в том же направлении выехала третья машина, которая обогнала первую на полтора часа позже, чем вторую.

–– Что же требуется, чтобы изложить эту ситуацию на математическом языке?

–– Нужно составить уравнение, а для этого надо обозначить неизвестную величину. Обозначим ее через х.

Здесь учащиеся останавливаются. От обилия неизвестных у них, что называется, «разбегаются глаза», но большинство предлагают обозначить через х расстояние между А и В. Учитель замечает, что объект №3 находится в соотношении и с объектом №1 и с объектом №2. Поэтому выгоднее обозначить через х км/ч не путь, а скорость третьей машины. Еще следует заметить, что эта задача, является задачей с переменной структурой, т.е. имеет несколько способов построения решения.

Далее разговор переходит на сравнение скоростей.

Учитель замечает, что математический язык не знает таких слов как «позже», «раньше», «быстрее», и т.д. он владеет только тремя словами, обозначающими связи между величинами. Это слова: больше, меньше, равно.

«…выехала третья машина, которая обогнала первую на полтора часа позже, чем вторую», это значит, что третья машина сначала догонит вторую машину, а потом первую.

Итак, обозначили через х км/ч скорость третьей машины. При этом заметим, что третья машина вышла только через полчаса после выхода первой и второй машин, которые двигались со скоростями соответственно 50 и 40 км/ч. Значит, чтобы догнать их, третья машина должна сократить расстояние между собой и машинами – соответственно 25 и 20 километров.

Ход рассуждений полезно представить в виде таблицы:

Величины

Ситуация

1-я

2-я

№3 догоняет №2

№3 догоняет №1

Прирост скорости, км/ч

х–40

>

х–50

Время, ч

20/(х–40)

<

25/(х–50)

Расстояние, км

20

25

На ?

На 3/2

Уравнение: .

З

На 1/2

адача. Расстояние от пункта А до пункта В равно 116 км. Из А в В одновременно отправляются велосипедист и мотоциклист. Скорость велосипедиста 12 км/ч, скорость мотоциклиста – 32 км/ч. Через сколько часов велосипедисту останется проехать в четыре раза больший путь, чем мотоциклисту?

Решение:

1. Анализ задачи.

В задаче идет речь о велосипедисте и мотоциклисте, которые отправляются одновременно в одном направлении из пункта А в В. Известно, что расстояние от А до В равно 116 км, скорость велосипедиста — 12 км/ч, скорость мотоциклиста — 32 км/ч. Требуется узнать, через сколько часов велосипедисту останется проехать в четыре раза больший путь, чем мотоциклисту.

Краткая запись задачи (в виде схематического чертежа) показана на рисунке 4, а.

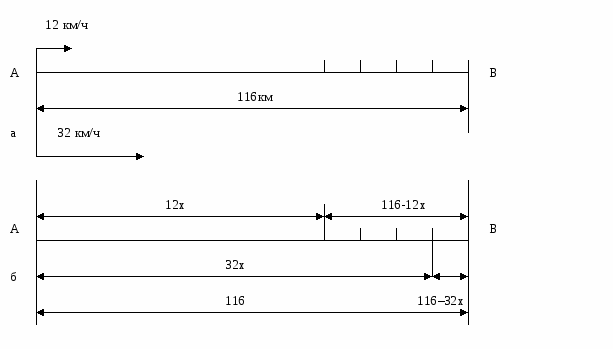
Рис. 4

2. Поиск пути решения задачи и составление плана ее решения.

Обозначим искомое число часов через х. Зная скорость мотоциклиста, можем узнать, какое расстояние он проедет за х ч, а затем, зная расстояние между пунктами A и B, найдем, какое расстояние останется проехать мотоциклисту до пункта В.

Зная скорость велосипедиста, можем узнать, какое расстояние он проедет за х ч, а затем найдем, какое расстояние ему останется проехать до пункта В.

По условию велосипедисту останется проделать путь, в четыре раза больший, чем мотоциклисту. Следовательно, мы можем составить уравнение, приравняв между собой путь, который осталось проехать велосипедисту, и путь, в четыре раза больший пути, который осталось проехать мотоциклисту.

Решив это уравнение, найдем, через сколько часов велосипедисту останется проделать путь, в четыре раза больший, чем мотоциклисту.

3. Осуществление плана решения задачи.

Пусть через х ч велосипедисту останется проделать в четыре раза больший путь, чем мотоциклисту. За это время мотоциклист проедет 32х км, значит, ему останется проехать до пункта В (116 – 32.x) км. Велосипедист за х ч проедет 12х км, значит, ему останется проехать до пункта В (116–12х) км (рис. 4б). По условию это расстояние в четыре раза больше, чем расстояние, которое останется проехать мотоциклисту. Следовательно, получаем уравнение

(116–32х)∙4=116–12х.

После несложных преобразований будем иметь:

464–128х=116–12х→116х=348→х=3.

Итак, искомое время равно 3ч.

4. Проверка решения задачи.

Через 3 ч мотоциклист проедет 32∙3=96 (км), останется 116–96=20 (км). Через 3 ч велосипедист проедет 12∙3=36 (км), останется до конца 116–36=80 (км). Найдем, во сколько раз велосипедисту останется сделать больший путь, чем мотоциклисту: 80:20=4 (раза). Расхождения с условием задачи нет. Задача решена правильно.

Ответ: через 3 ч велосипедисту останется сделать в 4 раза больший путь, чем мотоциклисту.

Также перед учащимися на этом этапе ставятся следующие вопросы:

• Какова главная идея решения данной задачи?

• Нельзя ли указать другие способы решения данной задачи?

• Почему рассмотренный способ решения является рациональным?

Таким образом, решение текстовых задач способствует развитию логического мышления учащихся, более глубокому усвоению идеи функциональной зависимости, повышению вычислительной культуры, более качественному и целостному восприятию школьной программы. Применение текстовых задач в процессе обучения способствует формированию у учащихся умений и навыков моделирования реальных объектов и явлений, что дает возможность приобретения новых знаний, необходимых в современном обществе.

Литература

1. Демидова Т.Е., Тонких А.П. Теория и практика решения текстовых задач. – М.: «ACADEMA», 2002

2. Дорофеев Г.В., Тараканова О.В. Постановка текстовых задач как один из способов повышения интереса учащихся к математике // Математика в школе-№5-1988-с.25

3. Лебедев В. Анализ и решение текстовых задач. Алгоритмизация/газ. Первое сентября – приложение. Математика, 2000, №41

4. Матушкина З. П. Задания, формирующие умение решать задачи/газ. Первое сентября – приложение. Математика, 1999, №42, ноябрь

5. Сафонова Л.А. О действиях, составляющих умение решать текстовые задачи.// Математика в школе-№8-2000-с.34