Формирование метапредметных умений (логических)

на примере решения текстовых задач на уроках математики в 5-8 классах.

Авторы:

Шелкова Татьяна Валерьевна,

учитель математики МКОУ СОШ № 1

г. Дубовки Дубовского муниципального

района, Волгоградской области,

Тютнева Татьяна Александровна,

учитель математики МКОУ

Горнобалыклейской СОШ Дубовского муниципального района Волгоградской области,

Подшибякина Наталья Евгеньевна,

учитель математики МКОУ

Горноводяновской СОШ Дубовского муниципального района Волгоградской области

СОДЕРЖАНИЕ

Введение.

Теоретические аспекты проблемы формирования логических умений на уроках математики.

Практическое применение методов формирования логических умений на уроках математики.

Заключение.

Список литературы.

ВВЕДЕНИЕ

Современные тенденции развития общества существенно повысили требования к уровню ожидаемых результатов образования. В настоящее время все больше требуются специалисты, отличающиеся мобильностью, самостоятельностью, изобретательностью, умеющие творчески подходить к решению проблем, принимать рациональное решение в ситуации выбора, способные к сотрудничеству.

Для решения жизненных задач человеку, помимо способностей и личностных качеств, необходимы различные умения, которые развивает учитель, работая с учениками на определенном предметном содержании. Но в жизни мы нечасто сталкиваемся с задачами, аналогичными предметным. Чаще всего жизненные задачи требуют метапредметных умений, которые в школьной практике называются общеучебными умениями. Как же формировать подобные умения? Это можно делать на отдельных предметах, последовательно развивая каждую группу умений (организационные, интеллектуальные, оценочные, коммуникативные). Но наибольшего эффекта мы достигнем, реализуя в школьном обучении межпредметные связи и интеграцию различных дисциплин, направленных на формирование общеучебных умений и навыков.

Математика в отличие от большинства других преподаваемых в школе дисциплин имеет предметом своего изучения количественные отношения и простран­ственные формы окружающего нас мира. Но для познания окружающего мира недостаточно лишь заметить связь между явлениями, необходимо установить, что эта связь является общим свойством вещей. На этой обобщенной основе человек решает конкретные познавательные задачи. Ответ на вопросы, которые нельзя разрешить путем непосредственного, чувственного отражения дает логическое мышление. Логическое мышление – характеризуется умением выводить следствия из данных предпосылок, умение теоретически предсказать конкретные результаты, обобщать полученные выводы. Благодаря развитию индивидуальных качеств мышления, человек правильно ориентируется в окружающем мире, используя ранее полученные обобщения в новой, конкретной обстановке.

Поэтому одной из важнейших задач, стоящих перед учителем, является развитие всех качеств и видов мышления, которые позволили бы детям строить умозаключения, делать выводы, обосновывая свои суждения, и, в конечном итоге, самостоятельно приобретать знания и решать возникающие проблемы.

1. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ПРОБЛЕМЫ ФОРМИРОВАНИЯ ЛОГИЧЕСКИХ УМЕНИЙ НА УРОКАХ МАТЕМАТИКИ.

Универсальные учебные действия классифицируются в три группы: управленческие, информационные и логические умения. Мы рассмотрим развитие логических умений обучающихся. В соответствии с типом задач, которые решаются в процессе мыслительной деятельности, принято условно выделять три основных вида мышления, которые тесно связаны между собой:

• наглядно-действенное (предметно-действенное) мышление – это процесс решения задач, в котором преобладают практические действия с реальными материальными предметами (например, приготовление кулинарного блюда, ремонт автомобиля).

• наглядно-образное мышление – это решение задач, в котором на первый план выступают действия с образами (например, создание модели свадебного платья, разработка архитектурного проекта, написание стихотворения).

• логическое (словесно-логическое, абстрактно-логическое, понятийное) мышление – это решение задач, которое сначала и до конца осуществляется на основе готовых знаний, выраженных в понятиях, суждениях и умозаключениях (например, решение физической задачи, доказательство теоремы).

По мнению психологов, эти виды умений формируются у человека в период с 2 до 10 лет, и развиваются всю последующую жизнь

Развитию логических умений, умению правильно рассуждать, делать выводы способствует решение текстовых задач в курсе математики, так как это упражнения, развивающие мышление; они способствуют воспитанию терпения, настойчивости, воли, пробуждению интереса к самому процессу поиска решения, дают возможность испытать глубокое удовлетворение, связанное с удачным решением, то есть формируют и мотивационную сферу.

Вообще, решение текстовых задач способствует достижению многих целей учебно-воспитательной работы с учащимися. В задачах заложены большие возможности для повышения общего и математического образования учащихся: развития смекалки, начал исследовательской работы, логического мышления.

В своей работе с учащимися 5-6 классов мы столкнулись с проблемой: при решении текстовых задач учащиеся видят только числа и стараются, как можно быстрее произвести различные математические действия с данными числами, не задумываясь над вопросами: «что дано в задаче?», «что надо найти?», «как это найти?» и так далее. Поэтому каждый раз при наборе нового 5 класса перед нами ставится цель: научить учащихся логически рассуждать, формулировать вопросы и строить цепочку рассуждений при решении различных текстовых задач. Решение задач выступает и как цель, и как средство обучения. Умение формулировать и решать задачи является одним из основных показателей уровня развития учащихся, открывает им пути овладения новыми знаниями.

Текстовая задача имеет образовательное, практическое ,развивающее и воспитательное значения

Образовательное значение текстовых задач: при их решении ученик знакомится с новой ситуацией, описанной в задаче, с применением математической теории к ее решению, познает новый метод решения и т.д. То есть приобретает математические знания, повышает свое математическое образование.

Практическое значение: при решении математических задач ученик обучается применять математические знания к практическим нуждам, готовится к практической деятельности в будущем, к решению задач, выдвигаемых жизнью. Поэтому мы стараемся предлагать учащимся задачи, практического содержания и задачи, связанные со смежными дисциплинами.

Значение в развитии мышления: решение задач приучает выделять посылки и заключения, данные и искомые, находить общее, и особенно в данных, сопоставлять и противопоставлять факты. Решение задачи должно быть полностью аргументированным. У учащихся формируется особый стиль мышления: соблюдение формально-логической схемы рассуждений, лаконичное выражение мыслей, четкая расчлененность хода мышления, точность символики.

Воспитательное значение: задача воспитывает и своим содержанием. При решении задач формируются: усидчивость, внимательность, сосредоточенность. Решение трудных задач требует от ученика проявления настойчивости в преодолении трудностей, упорства в достижении цели, аккуратности.

   Цель работы над задачами состоит в том, чтобы обеспечить лучшее усвоение включённых в программу вопросов теории, научить детей применять приобретённые теоретические знания на практике. При этом надо сформировать некоторые общие умения, необходимые для самостоятельного решения несложных жизненных задач, поддающихся «переводу» на язык математики. Необходимо развивать у учащихся умение рассуждать, основанное на способности отделить известное от неизвестного, установить существующие между ними связи, перевести эти связи с конкретного языка текстовой задачи на язык математических отношений и зависимостей. При решении текстовой задачи важно осознание учени­ком предстоящей деятельности с точки зре­ния ее учебного смысла. Школьник должен задуматься о значении, о цели, что он дела­ет, понять, зачем это необходимо. Поэтому уже первые шаги в решении задачи позво­ляют развивать такое регулятивное дейст­вие, как определение цели предстоящей де­ятельности. В процессе решения задач у ребят формируются умения и навыки моделирования объектов и явлений, развивается логическое мышление.

2. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ МЕТОДОВ ФОРМИРОВАНИЯ ЛОГИЧЕСКИХ УМЕНИЙ НА УРОКАХ МАТЕМАТИКИ.

Чтобы развить у учащихся логическое мышление, способность правильно и верно рассуждать, и как следствие, правильно решить любую задачу, учащимся надо усвоить основные этапы её решения.

Каждая задача – это единство условия и цели. Если нет одного из этих компонентов, то нет и задачи. Это очень важно иметь в виду, чтобы проводить анализ текста задачи с соблюдением такого единства. Это означает, что анализ условия задачи необходимо соотносить с вопросом задачи и, наоборот, вопрос задачи анализировать направленно с условием. Их нельзя разрывать, так как они составляют одно целое. Математическая задача – это связанный лаконический рассказ, в котором введены значения некоторых величин и предлагается отыскать другие неизвестные значения величин, зависимые от данных и связанные с ними определенными соотношениями, указанными в условии.

Любая текстовая задача состоит из двух частей: условия и требования (вопроса). В условии соблюдаются сведения об объектах и некоторых величинах характеризующих данные объекта, об известных и неизвестных значениях этих величин, об отношениях между ними. Требования задачи – это указание того, что нужно найти. Оно может быть выражено предложением в повелительной или вопросительной форме («Найти площадь треугольника» или «Чему равна площадь прямоугольника?»).

Решение любой задачи можно разбить на несколько этапов. Последовательное рассмотрение каждого, позволит учащимся без особых затруднений решать не только стандартные задачи, но и задачи повышенной трудности. В соответствии с каждым этапом учащиеся определяют цель своей деятельности:

1. Прочитать задачу, выделить условие и вопрос (требование).

2. Найти в условии данные и искомые.

3. Построить модель задачи.

4. Обдумать план решения задачи.

5. Записать решение.

6. Проверить решение задачи.

7. Написать ответ.

Ученик должен понять задачу. Но не только понять; он должен хотеть решить её. Прежде всего, должна быть понята словесная формулировка задачи. Ученик должен быть в состоянии указать главные элементы задачи - неизвестное, данное, условие. Таким образом, на первом этапе не обойтись без вопросов: Что неизвестно? Что дано? В чём состоит условие?

Ученик должен многократно, с разных сторон рассмотреть главные элементы задачи. Если с задачей связана какая-либо геометрическая фигура, он должен сделать чертёж и указать на нём неизвестное и данные.

Наблюдения показывают, что основная причина всех допускаемых детьми ошибок кроется в неправильной организации первичного восприятия задачи и её анализа без должного уяснения жизненной ситуации, отраженной в задаче, и без её графического моделирования. Поэтому в своей работе мы стараемся, чтобы каждый ученик умел не только записывать кратко условие задачи, но и иллюстрировать условие с помощью рисунка, схемы или чертежа.

Способ узнавания задачи среди других текстов является одним из приёмов, помогающих понять задачу. Другой приём – представление жизненной ситуации. Представлять ситуацию можно во время чтения и слушания задачи, а можно и после этих действий. Пониманию некоторых задач помогает представление себя участником ситуации, описанной в задаче. Сначала учитель «рисует мысленную картину», затем помогает кому-то из учеников, которые овладели приёмом, до тех пор, пока каждый самостоятельно не сможет представить и рассказать задачу товарищу. При этом выясняет с ребятами, что в данной «картине» существенно, важно с точки зрения математики, а что несущественно, значит, можно опустить.

Ещё один приём, помогающий понять задачу, - разбиение задачи на смысловые части и анализ каждой части. В каждой смысловой части выделяют: о чём говорится; что об этом говорится; сколько.

Приёмы переформулировки и моделирования - построение различных графических схем (чертежей, условных рисунков), которые отражают ситуацию, но не дают ответа на вопрос, а только помогают выбрать путь для его нахождения, также помогают понять задачу.

Приёмы работы над пониманием текста задачи способствуют развитию воображения, устной речи, осмыслению действий, помогают формированию умений определять понятия, анализировать, конкретизировать, выделять главное, существенное и несущественное с точки зрения математики. Рассмотрим пример, иллюстрирующий зависимость внимания от использования наглядного материала: «Скорость велосипедиста на 4 км/ч больше, чем скорость всадника. Через 2 ч расстояние между ними стало равным 54 км. Найти скорости велосипедиста и всадника, если первоначальное расстояние между ними равно 220 км».

В качестве наглядного материала может выступать изображение велосипедиста и всадника. Какова же при этом будет деятельность учеников? Очевидно, что они будут просто рассматривать изображенные фигуры. Но эта деятельность совершенно не связана с той, которая достигает цели обучения: в данном случае выделение общего способа решения задач «движение навстречу друг другу». Поэтому такой наглядный материал не только не помогает осуществлению цели обучения, а мешает этому. В этом случае лучше использовать схему:

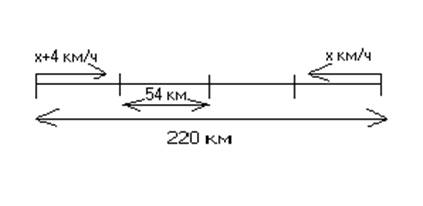
Чтобы каждый ученик на первом этапе понял задачу, уяснил, о чём эта задача, что в ней известно, что надо узнать, как связаны между собой данные, каковы отношения между данными и искомыми и так далее, необходимо использовать моделирование ситуации, отраженной в задаче.

Что же понимается под моделированием задачи? Моделирование в широком смысле слова - это замена действий с обычными предметами действиями с их уменьшенными образцами, моделями, муляжами, макетами, а также с их графическими изображениями: условными знаками, рисунками, схемами, чертежами. Наглядность, особенно графическая, нужна на всём протяжении обучения как важное средство развития более сложных форм конкретного мышления и формирования математических понятий, побуждает активно мыслить, рассуждать, искать другие пути решения.

Рассмотрим приемы вспомогательных моделей, которые могут быть представлены в виде схематического чертежа, чертежа, таблицы и краткой записи.

Пример. В первом бидоне краски в 2 раза больше, чем во втором. Если из первого бидона взять 2 л краски, а во второй добавить 5 л краски, то в обоих бидонах станет поровну. Сколько краски было в каждом бидоне первоначально?

Вспомогательная модель задачи (в виде схематического чертежа) показана на рисунке.

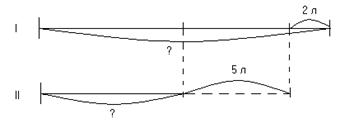
Пример. В первую неделю типография получила с фабрики шесть рулонов бумаги одного сорта и заплатила за них 204 р. Сколько рублей должна заплатить типография за месяц, если она получила 10 таких же рулонов бумаги того же сорта?

Число рулонов

Стоимость

Цена (руб)

6 шт

204 руб.

Одинаковая

10 шт

?

Пример: «Ваня, Петя и Серёжа пошли на рыбалку и поймали вместе 51 рыбку. Ваня поймал в 2 раза больше, чем Петя, а Сережа на 3 рыбки больше, чем Петя. Сколько рыбок поймал каждый мальчик?»

Вопросы, задаваемые учителем, по условию задачи: Что дано в задаче? Что неизвестно в задаче? Что известно о количестве рыб, пойманных Ваней? Что известно о количестве рыб, пойманных Сережей? В итоге диалога, учащиеся должны записать краткое условие задачи и ее графическое изображение:

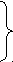Петя - ?

Ваня -?, в 2 раза больше 51 рыба

Серёжа -?, на 3 больше

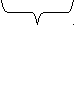
в 2 раза больше на 3 больше

Петя Ваня Серёжа

51 рыба

Следующий пример: «С одного участка собрали 1440 ц пшеницы, а с другого, площадь которого на 12 га меньше, - 1080 ц. Найти площадь первого участка, если известно, что на первом участке собирали пшеницы с каждого гектара на 2 ц больше, чем на втором».

Анализ задачи показывает, что в ней рассматривается сбор урожая пшеницы с двух участков, при этом этот сбор характеризуется тремя величинами: массой собранной пшеницы, площадью участка и урожаем с одного гектара. Исходя из этого, составим таблицу для схематической записи условий и требований задачи. Неизвестные величины, встречающиеся в задаче, запишем в таблице буквами, притом искомое обозначим буквой х:

Участки

Масса собранной пшеницы

Урожай с 1 га,

ц

Площадь участка, га

I

1440 ц

y+2

x

II

1080 ц

y

x-2

В этой схематической записи выделены все условия, их объекты и характеристики. Указано и требование задачи: найти площадь первого участка. В то же время эта запись очень компактная, наглядная и полностью заменяет саму формулировку задачи.

На следующем этапе процесса решения задачи важным моментом является выяснение стратегии решения задачи. Главный шаг на пути к решению задачи состоит в том, чтобы выработать идею плана. Сначала учащиеся строят план в виде вопросов, которые помогают им понять важность последовательных, осознанных действий и способствуют формированию умения последовательно анализировать данные и составлять план решения. Методика задавания вопросов заключается в следующем: начинать с общего вопроса или совета; затем, если это необходимо, нужно постепенно переходить к более частным и конкретным вопросам и советам. Советы должны быть общими, применимыми не только к данной задаче, но и к любым другим всевозможным задачам, если они имеют цель развить способности учащегося, а не просто частный технический навык решения задач.

Если ученик сам пришёл к идее решения задачи, постепенно шаг за шагом приходил к конечному результату, он не забудет ход своих мыслей. Основная задача учителя состоит в том, чтобы учащийся проверял правильность каждого своего шага, задавая каждый раз вопрос: «На основании, какого правила, свойства мы сделали тот или иной шаг?»

После определения требования задачи, составления плана ее решения, записи ре­шения наступает этап проверки. Оглядываясь назад на полученное решение, вновь рассматривая и анализируя результат и путь, которым они к нему пришли, ученики могут сделать свои знания более глубокими и прочными и закрепить навыки решения задач. Даже если учащиеся уверены в правильности полученного ответа, необходимо всегда осуществлять проверку своего решения. Это помогает контролировать и оценивать свою учебную дея­тельность и деятельность одноклассников. Формирование таких действий особенно эффективно при решении задач несколькими способами.

Одна из первых и главных обязанностей учителя состоит в том, чтобы не создавать у учащихся впечатления, что математические задачи мало связаны одна с другой и не связаны вообще больше ни с чем. Нужно представить учащимся возможность исследовать, как связана наша задача с другими, когда мы оглядываемся назад на её решение. Очень важно поощрять ребят придумывать случаи и задачи, к которым можно применить полученный метод или результат.

Следует отметить, что решение задач различными способами позволяет убедиться в правильности решения задачи, даёт возможность глубже раскрыть зависимости между величинами, рассмотренными в задаче.

При решении задач различными способами ученик привлекает дополнительную информацию, поскольку он непроизвольно выполняет в большем числе выборы суждений, хода мысли из нескольких возможных; рассматривается один и тот же вопрос с разных точек зрения. При этом полнее используется активность учащихся, прочнее и сознательнее запоминается материал.

При конструировании нового способа решения текстовых задач:

- организуем работу с учащимися таким образом, чтобы способ был сначала сконструирован словесно;

- затем учащиеся фиксируют его в виде модели (графической, знаковой);

- стараемся рассмотреть все версии учащихся;

- представить способ решения задачи в виде алгоритма.

В качестве основных способов решения текстовых задач в математике различают арифметический и алгебраический способы. При арифметическом способе ответ на вопрос задачи находится в результате выполнения арифметических действий над числами. Арифметические способы решения задач отличаются друг от друга одним или несколькими действиями или количеством действий, а также отношениями между данными, данными и неизвестным, положенными в основу выбора арифметических действий, или последовательностью использования этих отношений при выборе действий.

При алгебраическом способе ответ на вопрос задачи находится в результате составления и решения уравнения. В зависимости от выбора неизвестного для обозначения буквой, от хода рассуждений можно составить различные уравнения по одной и той же задаче. В этом случае можно говорить о различных алгебраических решениях этой задачи.

Нельзя забывать и про графический способ решения задач, который даёт возможность более тесно установить связь между арифметическим и геометрическим материалами, развить функциональное мышление детей.

Решение задач различными способами – дело непростое, требующее глубоких математических знаний, умения отыскивать наиболее рациональные решения.

При решении текстовых задач ученикам приходится самостоятельно ориентироваться в имеющихся знаниях, ставя перед собой вопрос: «Владею ли я теми знаниями, которые необходимы для решения задачи? Необходимы ли мне новые знания и уме­ния?»

Таким образом, в процессе обучения решению текстовых задач можно форми­ровать такие виды универсальных учебных действий: целеполагание, планирование, прогнозирова­ние, контроль, коррекцию, оценку и воле­вую саморегуляцию.

Можно сделать вывод, что, овладев этими учебными действиями на уроках математики, учащиеся перенесут их и на другие предме­ты: на уроках русского языка легко опреде­ляют цель задания, при написании изложе­ния — составляют точный план, при работе с деформированным текстом — контроли­руют и оценивают свою деятельность.

Недописанная фраза, незавершенная задача, недосказанное слово стимулирует работу учащихся. Ребята всех возрастов любят, когда уроки оживленны задачами - шутками, заданиями на внимание, старинными задачами. Язык, которым изложен текст старинных задач, смысловая нагрузка пробуждает любопытство, обостряет внимание. Ребятам нравится, когда учитель дает задание на исправление преднамеренных ошибок в решении, на восстановление частично стертых записей. Поэтому очень часто в качестве устной работы используем следующие задания:

- найти ошибки и исправить их;

- объяснить, незнание какого материала их повлекло;

- как можно избежать таких ошибок.

Для преодоления трудностей, возникающих по ходу решения задач, ребенку может быть предложен ряд упражнений, направленных на формирование необходимых вычислительных навыков. Особое внимание следует обратить приемам устного счета.

Пример устных задач в 5 классе по теме «Натуральные числа. Сложение и вычитание натуральных чисел»:

1. В магазине потратили 95 рублей; это на 20 руб. меньше, чем осталось. Сколько рублей осталось?

2. Рост Алеши 134 см., он на 3 см. выше Бори. Каков рост Бори?

3. Расстояние от дома до школы 300 м., от дома до кинотеатра 500 м. На сколько метров кинотеатр дальше от дома, чем школа?

4. В 100-литровую бочку налили 56 литров бензина, а потом еще 18 литров. Сколько литров бензина можно еще влить в бочку7

5. Сеня наклеивал марки в альбом. На первую страницу он поместил 18 марок. Из них 5 марок были польские, а остальные российские. На вторую страницу он наклеил 7 болгарских, а на третью - несколько словацких марок. Болгарских и словацких марок оказалось столько же, сколько российских. Сколько словацких марок наклеил Сеня?

6. Улитка ползет по столбу, высота которого 10 м. вверх, а ночью соскальзывает на 3 м. вниз. Через сколько дней доползет улитка до конца столба?

Пример устных задач по теме «Буквенные выражения»: В одном бидоне х л, а в другом – у л молока.

1. Расшифруйте выражения:

а) х + у

б) x + 3

в) y – 2

г) x – у

2. Расшифруйте равенства:

а) х + у = 90

б) x + 5 = y

в) 3x = y

г) x – 15 = y + 25.

Приведем пример работы над задачей в 6 классе:

Площадь участка поля 80 га, первый тракторист вспахал 40% этого участка, а второй 60% оставшейся части. Кто из них вспахал больше и на сколько га?

Работа над текстом задачи.

Интерес к решению задачи поднимется если разыграть ее в классе.

Вопросы на понимание содержания:

О чем говориться в задаче?

Что известно в задаче?

Можно ли сделать предположение кто вспахал больше и если отвечаем да, то сделайте его?

Известна ли площадь поля?

Что такое 1%? Как находиться?

За сколько процентов принимаем все поле?

Больше или меньше половины вспахал 1 тракторист?

Можем ли ответить на предыдущий вопрос про второго тракториста?

Как находиться оставшаяся часть поля?

Что будем сравнивать, отвечая на вопрос, кто из них вспахал больше?

Какой способ выберем для решения задачи?

Перевод текста на математический язык, установление соотношений между данными и вопросом.

Все поле изображаем прямоугольником

Это 100%. Разделим его на 2 части.

Первый тракторист вспахал 40% от всего поля. Сколько будут это в га обозначим знаком вопроса.

Вторая часть прямоугольника это остаток. Обязательно под ней написать слово остаток и поставить знак вопроса. Во второй части прямоугольника записываем 60% к слову остаток.

Сколько вспахал 2 тракторист обозначим знаком вопроса.

План решения.

Найти сколько вспахал первый тракторист.

Найти сколько осталось вспахать после первого тракториста.

Найти сколько вспахал второй тракторист.

Найти на сколько один тракторист вспахал больше другого?

Учащиеся записывают решение задачи.

По окончанию решения рефлексия и оценка решения задачи:

Понравилась ли задача?

Кто оказался прав в предположении?

Есть ли другой способ решения?

Придумайте 1-2 похожих на эту задачу, например, про работу на пришкольном участке, в летнем лагере.

Решение текстовых задач даёт возможность формировать у учащихся умение записывать реальные жизненные ситуации на математическом языке, что способствует развитию логического мышления, овладение операциями мышления - анализом, синтезом, обобщением, воспитывает такие качества личности, как самостоятельность, настойчивость и творчество.

При решении текстовых задач учащиеся получают опыт работы с величинами, постигают взаимосвязи между ними, получают опыт применения математики к решению практических задач. Использование арифметических способов решения задач развивает смекалку и сообразительность, умение ставить вопросы, отвечать на них, то есть развивает естественный язык, готовит школьников к дальнейшему обучению. Использование исторических задач и разнообразных старинных (арифметических) способов их решения не только обогащает опыт мыслительной деятельности учащихся, но и позволяет им осваивать важный культурно-исторический пласт истории человечества, связанный с поиском решения задач. Это важный внутренний (связанный с предметом), а не внешний (связанный с отметками, поощрениями и т.п.) стимул к поиску решения задач и изучению математики. Решение текстовых задач дает положительный результат при условии, что решаются они на каждом уроке, и используются разные способы решения, если среди учащихся проводятся различные конкурсы, блиц-турниры и другие формы поддержки интереса к решению текстовых задач.

ЗАКЛЮЧЕНИЕ.

Интеллект человека, в первую очередь определяется не суммой накопленных им знаний, а высоким уровнем логического мышления. Поэтому необходимо научить детей анализировать, сравнивать и обобщать информацию, полученную в результате взаимодействия с объектами не только действительности, но и абстрактного мира.

Метапредметный урок нельзя построить по жесткому плану. На таком уроке учителю надо всегда быть готовым к тому, что здесь всегда есть место импровизации. Такой урок гибок и во многом зависит от взаимодействия учителя с учащимися.

Пытаясь найти решение задачи, дети должны научиться с нашей помощью поменять свой взгляд на задачу, думать о математике как о предмете, где каждому есть возможность выразиться.

Математику любят в основном те ученики, которые умеют решать задачи. Следовательно, научить детей владеть умением решения задачи, мы окажем существенное влияние на их интерес к предмету и на развитие логического мышления.

Решение задачи – это упражнение, развивающее мышление; оно способствует воспитанию терпения, настойчивости, воли, пробуждению интереса к самому процессу поиска решения, даёт возможность испытать глубокое удовлетворение, связанное с удачным решением, то есть формирует мотивационную сферу. Решение задач – одно из средств, помогающих формированию у детей таких важнейших качеств личности, как любовь к труду и потребность трудиться.

ЛИТЕРАТУРА

1. Бантова М.А. Решение текстовых арифметических задач.//-М.: Просвещение,1989.

2. Баринова О.В. Дифференцированное обучение решению математических задач. // М.: Просвещение, 1999.

3. Василевский А. Б. Обучение решению задач по математике. Минск, 1988.

4. Вялова С. Как составить и решить задачу. // М.: Просвещение, 1998.

5. Воровщиков С.Г. Как эффективно развивать логическое мышление младших школьников / С.Г. Воровщиков, Е.В. Орлова, Г.П. Каюда, Н.В. Гладик и др.: 2-е изд. М., 2009.

6. Шевкин, А.В. Текстовые задачи в школьном курсе математики [Текст] / А.В. Шевкин // Математика (приложение к газете "1 сентября"). - 2005. - № 11, 17, 19

7. И. Володарская, Н. Салмина. Общий прием решения математических задач [Текст] / И. Володарская, Н. Салмина // Математика (приложение к газете "1 сентября"). - 2005.

8. Газарян Р. Задача, как обучающая модель // Г. Математика. – 2003. - №11.

22