Муниципальное автономное общеобразовательное учреждение

«Гимназия №8»

Пермский край

Конспект урока по геометрии

в 8 классе
«Подобие треугольников»

подготовила

учитель математики

Коньшина Елена Викторовна

г. Пермь
2014

Тема урока «Подобные треугольники»

Тип урока: урок изучения нового материала.

Цели урока:

• формирование понятия подобия треугольников;

• развитие пространственных представлений и изобразительных умений;

• развитие умения поиска нужной информации для решения математической проблемы и представления ее в понятной форме;

• формирование у учащихся практических навыков определения высоты объектов.

Задачи урока:

• образовательные (формирование познавательных УУД):

научить в процессе реальной ситуации использовать подобие треугольников для нахождения высоты объекта;

• воспитательные (формирование коммуникативных и личностных УУД):

формировать умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность;

• развивающие (формирование регулятивных УУД):

формировать умение обрабатывать информацию и ранжировать ее по указанным основаниям; представлять информацию в табличной форме; выбирать способы решения задач в зависимости от конкретных условий; научить контролю и оценке процесса и результатов деятельности.

Краткое описание хода урока:

В начале урока класс делится на группы. Каждая группа получает кейс. Дальнейшая работа ведется в группах. Учащиеся читают текст и отвечают на вопросы к нему. В конце урока группы представляют информацию в доступной форме. Учитель подводит итоги и оценивает работу групп.

В результате изучения нового материала ученики должны:

• знать определение пропорциональных отрезков, подобных треугольников;

• уметь выполнять чертежи; приводить примеры объектов реального мира, моделями которых являются геометрические понятия; соотносить объекты с их описаниями, чертежами;

• владеть навыком нахождения высоты объекта c использованием подобия треугольников.

Ход урока

1.Организационный момент (2 мин.).

После приветствия учитель предлагает ученикам поделиться на группы по четыре человека. Раздать на каждую парту кейс.

2.Мотивация к деятельности и актуализация знаний учащихся (3 мин.).

Одинаковые по форме, но разные по величине фигуры называются подобными. Подобие фигур издавна применялось на практике, например при землемерных работах. Фалес Милетский - человек, который обрел славу одного из «семи мудрецов» древности. Это древнегреческий философ, который отличился успехами в области астрономии, а также математики и физики. Фалес Милетский смог определить высоту пирамиды по ее тени, чем очень удивил фараона. Прочитайте текст и ответьте на вопросы.

3. Работа в группах (20 мин.).

В процессе работы учащиеся решают проблему. Далее идет выработка общей позиции, оформляется текст выступления от группы.

4. Заключительная презентация результатов аналитической работы (15мин).

5. Обобщающее выступление учителя – анализ ситуации; оценивание учителем учащихся (5мин.).

Кейс «Подобие треугольников»

Вид кейса: печатный.

Тип кейса: практический.

В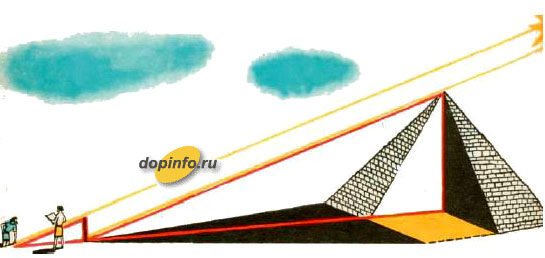еликая Пирамида Хеопса (около 2590-2568 годы до н. э.), одно из семи чудес света, является фантастическим шедевром инженерного искусства. С пирамидой связано много таинственных историй и легенд.

В

Рис. 1. Измерение высоты пирамиды Фалесом

один из солнечных дней Фалес вместе с главным жрецом храма Изиды прогуливался мимо пирамиды Хеопса.

– Знает ли кто-либо, какова её высота? – спросил он.

– Нет, сын мой, – ответил ему жрец, – древние папирусы не сохранили нам этого.

– Но ведь определить высоту пирамиды можно совсем точно и прямо сейчас! – воскликнул Фалес.

– Вот смотрите, – продолжал Фалес, – именно в это время, какой бы мы предмет не взяли тень от него, если поставить его вертикально, точно равна высоте предмета.

Вопросы:

1. Используя рис.2, объясните, какие измерения сделал Фалес, чтобы определить высоту пирамиды?

2.Найдите высоту пирамиды, если длина тени пирамиды от основания равна 68 локтей, сторона основания равна 500 локтей, а высота шеста и длина его тени 3 локтя (у египтян было три единицы длины: локоть (466 мм), равнявшийся семи ладоням (66,5 мм), которая, в свою очередь, равнялась четырем пальцам (16,6 мм)).

3. В чем вы видите плюсы и минусы такого способа определения высоты.

4.Объясните, пользуясь, рис. 2 и 3, как еще можно измерить высоту объекта?

Рис. 2. Измерение высоты равнобедренным треугольником

Рис. 3.Измерение высоты с помощью зеркала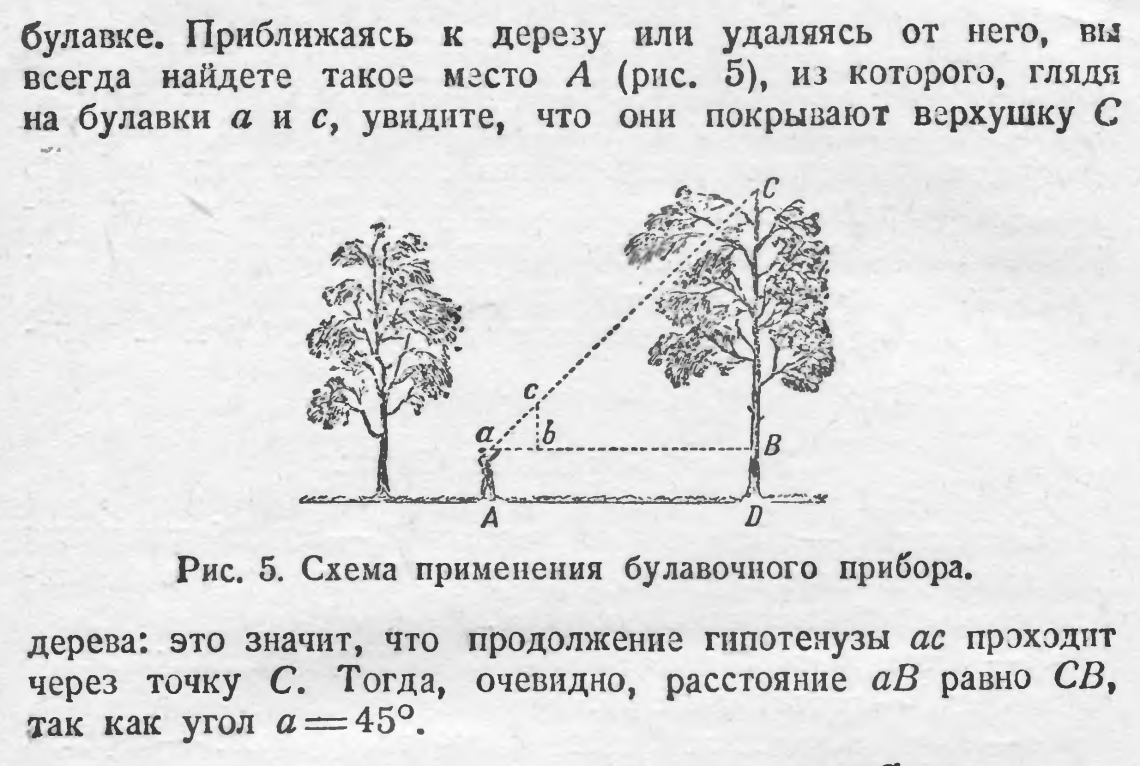

5. Сделайте в тетради чертеж по рис. 3. Как называются данные треугольники? Запишите определение. Найдите и запишите сходственные стороны треугольников. Составьте отношения сходственных сторон.

6. Предложите свой способ измерения высоты объекта.

7. Домашнее задание.

Проведите по схеме исследование:

• Выберите для исследования объект: дерево, дом, фонарный столб.

• Определите высоту объекта двумя способами.

• Добавьте и исследуйте свой объект.

Результаты запишите в таблицу по форме:

Объект

Высота при помощи зеркала

Высота при помощи равнобедренного треугольника

Свой способ

дерево

свой объект

Сделайте выводы (выполните по плану):

• Есть ли сходство в способах?

• Какие теоретические сведения из геометрии применяются при определении высоты объекта?

• Какой способ вам понравился? Почему?

• Cлучается, что почему-либо неудобно подойти вплотную к основанию измеряемого объекта. Можно ли в таком случае определить его высоту?

Информационный материал

Еще в Древнем Египте при строительстве пирамид использовались математические знания в области пропорций. В толковом словаре можно найти следующее определение этого термина пропорция (лат. proportio – «соотношение») – это отношение между несколькими (двумя и более) соразмерными величинами [3].

Данный термин используется не только в математике, но и медицине, искусстве, архитектуре и других областях научной и культурной деятельности.

Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских и египетских памятниках. В сохранившейся погребальной камере отца Фараона Рамсеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров. Учение о подобии фигур на основе теории отношений и пропорции было создано в Древней Греции в V—IV вв. до н. э. Оно изложено в VI книге «Начал» Евклида(III век до нашей эры), начинающиеся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны»[1, 282].

Геометрия, 7 – 9: учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 18-е изд. – М.: Просвещение, 2010.

Примерные ответы

1.Фалес измерил высоту шеста, длину тени шеста и пирамиды.

2.Высота пирамиды 318 локтей=148188 мм.

3.К плюсам можно отнести простоту вычисления, к минусам- наличие тени.

4.По рис.2 из подобия треугольников получаем . По рис.3 из подобия треугольников получаем .

5.Сходственные стороны AB и ЕD, AC и CE, ВС и CD.

6. Например, с помощью шарика с гелием, с помощью фотографии объекта.

7. Если основание предмета недоступно, то можно поступить так: на прямой, проходящей через основание Н предмета, отметим две точки В и С на определенном расстоянии а друг от друга и измерим углы АВН и АСВ: АВН = , АСВ = , ВАС = – . Эти данные позволяют определить все элементы треугольника АВС; по теореме синусов находим АВ:

Из прямоугольного треугольника АВН находим высоту АН предмета:

АН = АВ sin . Тогда . Это один из возможных способов. Учащиеся могут привести свои. Главное, что измерения ведутся из двух точек.

Список использованной литературы

1. Глейзер Г.И. История математики в школе. – М.:Издательство «Просвещение», 1964.

2.Перельман Я. И. Занимательная геометрия.– М.:Государственное издательство технико-теоретической литературы, 1950.

Использованные материалы и Интернет-ресурсы

1. Общий толковый словарь русского языка [Электронный ресурс]. – Режим доступа: http://tolkslovar.ru/p22702.html

2. Рисунок 1 [Электронный ресурс]. – Режим доступа: http://www.dopinfo.ru

3. Рисунки 2 и 3. – Перельман Я. И. Занимательная геометрия.– М.:Государственное издательство технико-теоретической литературы, 1950