Муниципальное бюджетное образовательное учреждение

«Средняя общеобразовательная школа №19»»

г. Северодвинска Архангельской области

Развитие мотивационной сферы учащихся на уроках математики

(обобщение опыта работы)

подготовила

учитель математики

Прелова Лариса Викторовна

г. Северодвинск

2014

«Сделать учебную работу насколько возможно интересной для ребенка и не превратить ее в забаву - эта одна из труднейших и важнейших задач дидактики».

К.Д. Ушинский

Актуальность, новизна.

Развитие мотивационной сферы-одна из важнейших задач современного учителя. В настоящее время, когда учащимся доступен Интернет, современные информационные технологии, мобильная связь, заинтересовать ребенка на уроке очень сложно. Учитель должен не только донести важную и полезную информацию до учащегося, но и уметь представить ее так, чтобы это привлекло внимание, заставило задуматься.

Учитель в современной школе выступает не столько «информатором», сколько руководителем, наставником, направляющим учащихся к новым знаниям. Китайская мудрость гласит: «Скажи мне, и я забуду, покажи мне, и я запомню, дай мне сделать самому и я пойму».

Для развития мотивационной сферы существует множество приемов. Эти приемы используются в зависимости от возраста ребят, учебного материала, особенностей класса. Разнообразные работы активизируют учебную деятельность школьников, воспитывая у них активность, самостоятельность мышления, умение применять знания в процессе обучения. Положительный эффект в обучении дают различные дидактические игры, творческие задания, практические работы, занимательные задачи…Новизна данной темы заключается в том, что известные всем приемы и методы современный учитель может применять в новой интерпретации с использованием новейших информационных технологий.

Цель, возможность использования данного опыта в работе.

Цель: обобщение опыта работы при обучении математике учащихся общеобразовательных классов в вопросах развития мотивационной сферы и познавательной активности. Данный опыт возможно использовать на уроках математики, алгебры, геометрии; при индивидуальной работе с учащимися. Представленные компоненты системы работы возможно адаптировать для классов с различным уровнем успеваемости.

Используемые методы, на мой взгляд, позволяют учителю решать следующие задачи в учебном процессе:

1. Мотивируют учащихся на самостоятельную работу.

2. Развивают творческое мышление.

3. Формируют навыки практической и исследовательской деятельности.

4. Систематизируют знания по предмету.

Перечень компонентов системы работы

1. Одной из основных и первоначальных задач при обучении математике является выработка у обучающихся навыков хорошего счета. Однако, однообразие заданий в виде примеров на вычисление притупляет интерес как к счету, так и к урокам вообще. Поэтому учителю необходимо иметь в запасе арсенал различных приемов, направленных на выработку вычислительных навыков учащихся и в то же время не злоупотребляющих вниманием ребят. Здесь можно использовать различные игры: «математическое домино», круговые примеры, эстафеты, игру «Рыбалка» (из нескольких предложенных примеров ученики 1 варианта «вылавливают» примеры с ответом 5, а ученики 2 варианта- с ответом 6). Математическое домино, круговые примеры позволяют ребятам осуществлять самоконтроль, а учителю облегчают проверку. Математическая эстафета вызывает дух соревнования. Большой интерес у ребят вызывают задания на исправление преднамеренно сделанных ошибок в решении, на восстановление частично стертых записей, на заполнение «форточек» (пример: закрыть «форточки», чтобы равенство получилось верным 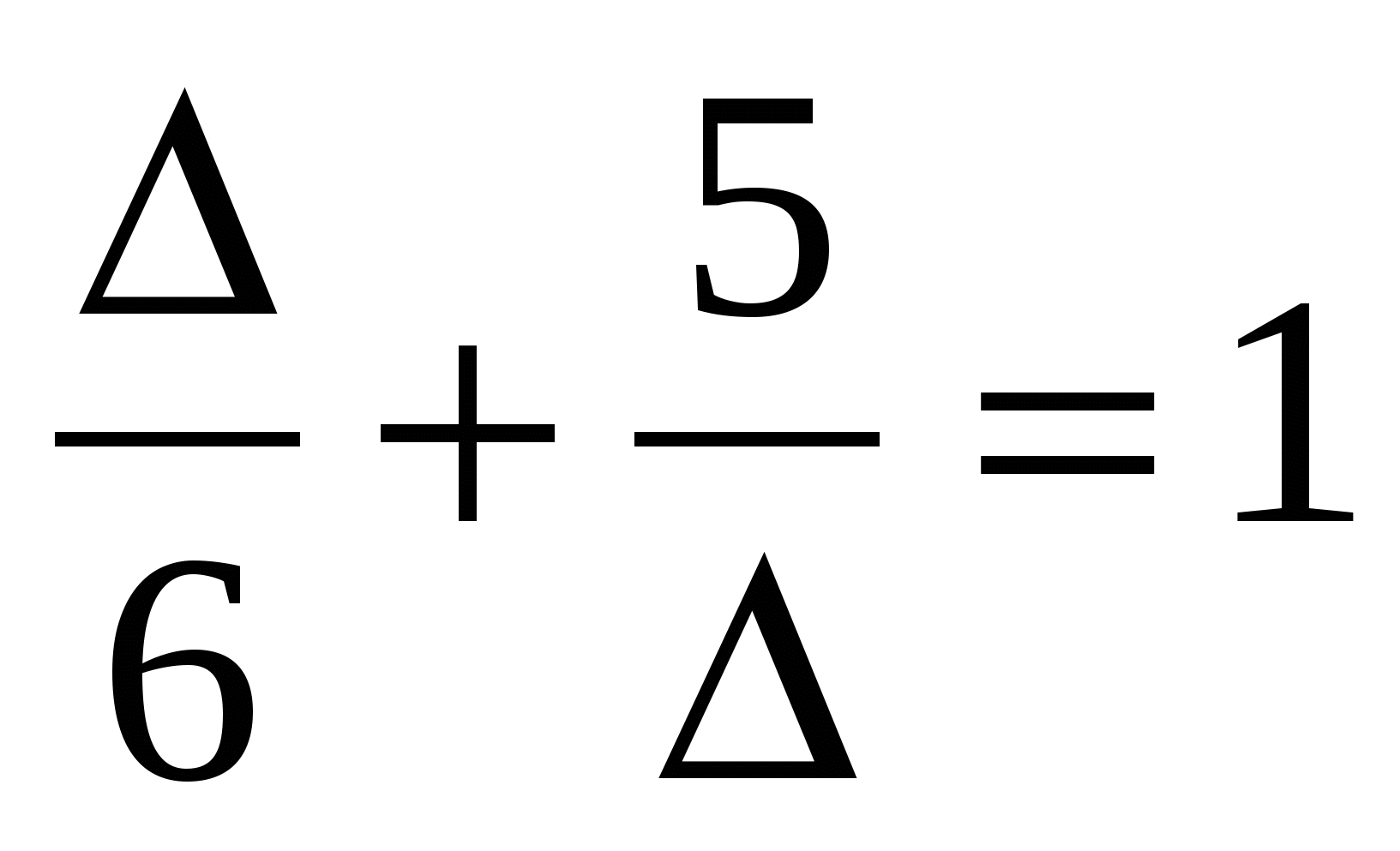). Игровой компонент, соревнование, дух творчества должны присутствовать органически на всех уроках, тогда занятие вызовет интерес, желание работать и знать предмет. Использование современного мультимедийного оборудования позволяет проводить данную работу быстро, давая учителю возможность оперативно представлять правильные ответы, контролировать полученные у учеников результаты.

2. -3

   -2

   -1

   9

   
   

   1

   
   

   -8

   -1

   4

   8

   16

   32

   64

   128

   256

   512

   
   

   Важной составляющей всех уроков математики являются задания на тренировку математической памяти и «зоркости». Большинство таких заданий основаны на нахождении закономерностей (пример: найти закономерность и вставить недостающее значение

Учащимся можно предлагать как готовые закономерности, так и возможность составлять их самостоятельно. Данный подход позволит активизировать творческое направление работы, внести дифференцированный компонент в задания.

3. Огромную роль при мотивации учащихся к деятельности играют практические задания. Склеивание из бумаги треугольной призмы, параллелепипеда, пирамиды позволяют школьникам усвоить понятие пространственной фигуры. Я в своей работе предлагаю пошаговый алгоритм для выполнения данных заданий, где каждый этап представлен для учащихся на интерактивной доске. Такой подход позволяет большинству ребят справиться с работой, исправить ошибки, ориентируясь на пошаговые модели, представленные на доске.

Благодатной почвой для формирования практических навыков является работа с транспортиром: измерение углов, вырезание углов определенной градусной меры, деление угла на два равных. Интерактивная модель транспортира позволяет учителю наглядно продемонстрировать алгоритм пользования этим инструментом, представить механизмы построения острых, тупых, прямых углов. (Приложение 1)

4. Огромный интерес у школьников 5-7 классов вызывают уроки-сказки, уроки-путешествия (Приложение 2) Данные формы занятий вызывают не только интерес к математике, но и способствуют созданию положительной эмоциональной обстановки на уроке. Нестандартные формы урока ценны тем, что наряду с формированием интереса к предмету, способствуют накоплению учебных знаний, навыков и умений. Для развития мотивационной сферы учащихся очень полезны интегрированные уроки (математика-физика, математика-биология, математика-химия). Данный подход позволяет учителю не только активизировать познавательную деятельность, но и продемонстрировать межпредметные связи, что является неотъемлемой задачей обучения.

Уроки-путешествия я часто использую при изучении темы «Задачи на движение» (Приложение 3).Смоделированная ситуация позволяет учащимся в игровой форме усвоить понятия расстояния, скорости и времени, что необходимо для составления математической модели при решении задачи.

Уроки-сказки особенно актуальны в 5-6 классах при решении сюжетных задач. Данная форма занятия не только делает учебный процесс увлекательным, но и снимает эмоциональное напряжение, страх учащихся перед задачей.

5. Очень важным для развития мотивационной сферы является наличие на уроке нестандартных заданий: задач-шуток, задач-фокусов.

Задачи-шутки:

1. Что легче: 1 кг гвоздей или 1 кг ваты?

2. Одно яйцо варят 4 минуты. Сколько минут варят 5 яиц?

3. Бежала тройка лошадей. Каждая лошадь пробежала 5 км. Сколько км проехал ямщик?

Задачи-шутки заставляют ученика не относиться к решению формально, зачастую не понимая его сути, а искать подвох, внимательно вчитываться в условие, моделировать ситуацию.

Задачи-фокусы:

1. Задумайте число, умножьте его на 4; результат умножьте на 0,25. Назовите ответ, я назову задуманное вами число. Объясните, почему я смогла это сделать.

2. Задумайте трехзначное число и припишите к нему точно такое же число. Получившееся шестизначное число умножьте на 2, а результат разделите сначала на 7, а потом, что получится на 11 и, наконец, на 13. Спросите, какой получится ответ, и вы назовете задуманное число, разделив названный ответ на 2.

Подобные задачи очень интересны для ребят всех возрастов. Они пробуждают естественное любопытство и заставляют искать объяснение фокусу. Полезны такие задания и для формирования вычислительных навыков. Учитель, расширяя мотивационную сферу школьников, не только решает дидактические задачи, но и дает возможность почувствовать красоту предмета, его многопрофильность, разнообразие. Математика перестает быть пугающим своей сложностью предметом, становиться интересной, занимательной, жизненно необходимой.

6. Современный учитель должен использовать при обучении математике естественное любопытство и желание разобраться в интересующем вопросе. Для учащихся старших классов предпочтительно постановка проблемы при изучение конкретной темы, которую ребята захотят решить с помощью математических знаний. Так при изучении арифметической прогрессии я вспоминаю рассказ К. Гаусса о том, как он устно сосчитал сумму 1+2+…100. Ставлю перед ребятами вопрос: как сделать это моментально? При введении понятий синуса и косинуса ставлю перед учениками проблему взлете самолета, не задев верхушек деревьев. При изучении задания плоскости, спрашиваю, почему различные измерительные приборы ставят на треногу? Изучая формулы площадей поверхностей, решаем вопрос о количестве необходимой краски для покраски деталей, имеющих различную геометрическую форму…

Используемый мной метод проблемного обучения составляет органическую часть системы проблемного обучения. Основой метода является создание проблемных ситуаций, формулировка проблем, подведение учащихся к проблеме. Проблемная ситуация включает эмоциональную, поисковую и волевую сторону. Её задача - направить деятельность учащихся на максимальное овладение изучаемым материалом, обеспечить мотивационную сторону деятельности, вызвать интерес к ней.

Активная мыслительная деятельность всегда связана с решением определённого задания. Мыслить человек начинает, если у него возникла потребность что-то понять, что-то осуществить. Мышление начинается с проблемы или вопроса, противоречия. Проблемной ситуацией определяется привлечение личности к мыслительному процессу, который всегда направлен на решение некоторой задачи.

7. Учитель в современной школе всегда должен идти в ногу со временем, проводить параллели своего предмета с событиями, проходящими в городе и стране. Это позволяет ребенку понимать связь изучаемых предметов с жизненными ситуациями, формирует его жизненный опыт и тем самым способствует расширению мотивационной сферы. Накануне олимпийских игр, проводимых в Сочи в 2014 году, считаю возможным предлагать учащимся задачи с олимпийской тематикой, например,

Задача 1: Олимпийский огонь зажгут в Олимпии (Греция) за несколько месяцев до открытия Игр и доставят в город Сочи. Факел XXII Олимпийских игр, корпус которого выполнен методом литья из алюминиевого сплава, преодолеет более 65 тысяч километров в руках спортсменов, на автомобилях, поездах, самолётах, а также на русской тройке и оленьих упряжках.

• Найдите значение выражения (22 · 2014 – 44290) : 10, и вы узнаете, сколько весит (кг) факел XXII Олимпийских игр.

• Найдите значение выражения (14193 - 2014 · 7) : 100, и вы узнаете высоту факела (м).

• Составьте самое маленькое трёхзначное число из цифр 3, 1, 2

(цифры не должны повторяться) и вы узнаете, сколько дней будет длиться Эстафета Олимпийского огня «Сочи 2014» (начало эстафеты - 7 октября 2013 года, окончание – 7 февраля 2014 года).

• Найдите чётное двузначное число, сумма цифр которого равна 12, а при делении цифры десятков на цифру единиц получается 2, и вы узнаете, сколько городов, включая город Сочи, озарит Олимпийский огонь.

Задача 2: Пятнадцать зимних спортивных дисциплин, объединённых в семь олимпийских видов спорта, включены в программу зимних Олимпийских игр 2014 года. Сосчитайте, какое количество комплектов медалей будет разыграно на Олимпиаде в Сочи.

1. Биатлон – 11

2. Бобслей: бобслей – 3; скелетон – 2

3. Кёрлинг – 2

4. Коньковые виды спорта:

скоростной бег – 12; фигурное катание – 5; шорт-трек – 8

5. Лыжные виды спорта:

горнолыжный спорт – 10; лыжное двоеборье – 3; лыжные гонки – 12; прыжки с

трамплина – 4; сноубординг – 10; фристайл – 10

6. Санный спорт – 4

7. Хоккей – 2

Приложение 1

Приложение 2

Фрагмент урока-сказки по теме «Масштаб» (с использованием сказки П. Ершова «Конек-горбунок»)

Предложены задачи на применение действий с дробями, нахождение среднего арифметического, определение масштаба и построение треугольника.

За горами, за лесами,
За широкими морями,
Не на небе - на земле
Жил старик в одном селе.
У старинушки три сына:
Старший умный был детина,
Средний сын и так и сяк,
Младший вовсе был дурак.
Братья сеяли пшеницу
Да возили в град-столицу:
Знать, столица та была
Недалече от села.

Задача 1.

Узнать расстояние от села до столицы, если известно, что на карте расстояние между этими пунктами 3 см, а масштаб карты 1:5000

Там пшеницу продавали,
Деньги счётом принимали
И с набитою сумой
Возвращалися домой.

Задача 2.

Определить среднюю урожайность пшеницы, которую снимал с полей крестьянин с сыновьями, если с первого поля сняли 2,1ц; со второго поля-1,9ц; с третьего поля-1,8ц; с четвертого поля-2,2ц.

Задача 3.

Сколько выручено денег, если цена одного центнера зерна составляла 1000 рублей?

«Что, Иванушка, невесел?
Что головушку повесил?» -
Говорит ему конёк.
«Помоги мне, горбунок!
Видишь, вздумал царь жениться,
Знашь, на тоненькой царице,
Так и шлёт на окиян, -
Говорит коньку Иван.

…
Тут конёк: «Сказать по дружбе,
Это - службишка, не служба;
Служба всё, брат, впереди!
Ты теперя спать поди;
А назавтра, утром рано,
Мы поедем к окияну».

Задача 4.

Начертить маршрут по которому ехал Иванушка, если известно, что перстень находится в городе М, терем с Солнцем и Месяцем в городе К, а сам царь живет в городе В. Известно, что МВ=5,3; КМ=2,5; угол М равен 115 градусов.

Приложение 3

Фрагмент урока-путешествия «Задачи на движение. Действия с десятичными дробями»

1 этап

Путешествие будет проходить по воде на катерах. Выберем капитанов каждого катера. Задание для капитанов: собственная скорость катера 15км/ч, а скорость течения 3,5км/ч. Найти скорость катера по течению и против течения.

2 этап

Покупаем билеты в кассе. Каждый вариант решает по цепочке примеры своего столбика: 36+9,1= 8,2+4=

18+2,7= 15+3,6=

29-13,4 30-2,4=

3 этап

Занимаем свои места и начинаем движение. Капитаны докладывают, с какой скоростью двигаются катера. Все пассажиры должны принять участие в движении катеров. Для этого необходимо подбросить горючего. Каждый правильный ответ к заданию - это капелька горючего.

Округлить: а) до десятых 6,713; 2,754; 40,076

б) до сотых 0,534; 32,743; 1,507

4 этап

Катера сели на мель. Решив уравнение, исправьте ситуацию:

Х+2,8=3,72+0,38

5 этап

Завершая путешествие, каждая команда должна решить задачу: какой путь вы прошли, если двигались 2 часа по течению реки и 3 часа против течения реки?

Список использованной литературы

1. Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка, М.:Просвещение 1988

2. Журнал «Математика в школе» 2009

3. Возлинская М.В. Задачник. Нестандартная математика в школе, М.:Лайда 1993

4. Журнал «Квант» 1990

5. Гальперин Г.А., Толпыго А.К. Московские математические олимпиады, М.:Просвещение 1988

Использованные материалы и Интернет-ресурсы

1. http://gorinalw.3dn.ru/SERII/Olimp-SOCHI/Stend-1.pdf