по Математике 2
Содержание
1.Введение в анализ и дифференциальное исчисление функции одного переменного
Вычислить предел
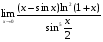
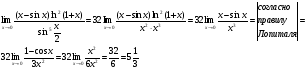
Найти асимптоты функции
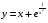
Отметим, что данная функция не существует при 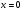 .
.
Исследуем прямую 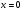 на вертикальную асимптотичность:
на вертикальную асимптотичность:
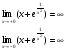
Отсюда следует, что прямая 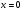 является вертикальной асимптотой.
является вертикальной асимптотой.
Проверим функцию на существование горизонтальных асимптот:
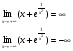
Отсюда следует, что горизонтальные асимптоты отсутствуют.
Проверим функцию на существование наклонной асимптоты:
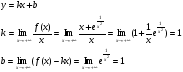
Отсюда следует, что функция имеет наклонную асимптоту 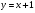
Таким образом, данная функция имеет вертикальную асимптоту 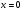 и наклонную асимптоту
и наклонную асимптоту 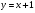
Определить глобальные экстремумы
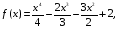 при х[-2,0]
при х[-2,0]
Для определения глобальных экстремумов, вычислим производную 1-го порядка для данной функции:
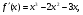
Найдем значения аргумента, при которых данная производная будет равна 0:
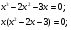
Отсюда имеем 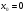 ;
;
Продолжая решение: 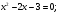
По теореме Виета, получим:
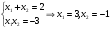
По условию задания глобальные экстремумы определяются на отрезке х[-2,0]. Таким образом, имеем, что на отрезке [-2, -1] значение производной отрицательно, на отрезке
[-1, 0] – положительно. Таким образом, при 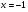 , функция принимает минимальное значение на заданном отрезке:
, функция принимает минимальное значение на заданном отрезке: 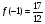
Исследуем значения функции на концах заданного отрезка: 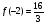 ,
, 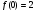
Таким образом, при 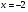 функция принимает максимальное значение на заданном отрезке.
функция принимает максимальное значение на заданном отрезке.
Ответ: 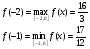
Исследовать на монотонность, найти локальные экстремумы и построить эскиз графика функции
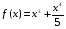
Для исследования функции на монотонность, найдем производную 1-го порядка:
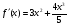 , Определим значения аргумента, при которых производная равна 0
, Определим значения аргумента, при которых производная равна 0
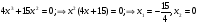
На промежутке 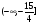 - функция монотонно убывает
- функция монотонно убывает
На промежутке 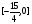 - функция монотонно убывает
- функция монотонно убывает
На промежутке 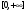 - функция монотонно возрастает
- функция монотонно возрастает
То есть при х=0, функция принимает минимальное значение у=0
Таким образом, эскиз графика функции, выполненный по условию задания, выглядит следующим образом:
Х
Y
Найти промежутки выпуклости и точки перегиба функции
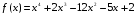
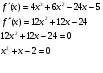
По теореме Виета:
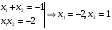
Далее определим промежутки выпуклости функции
На промежутке 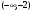
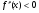 ; - выпуклость вверх
; - выпуклость вверх
На промежутке 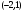
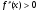 ; - выпуклость вниз
; - выпуклость вниз
На промежутке 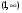
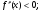 - выпуклость вверх
- выпуклость вверх
Значения функции в точках перегиба: 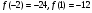
Тогда точки перегиба функции: 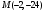 и N
и N 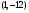
2. Дифференциальное исчисление функций и его приложение
Провести полное исследование свойств и построить эскиз графика функции
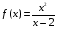
Функция
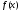 не является четной, не является нечетной. Функция не периодична.
не является четной, не является нечетной. Функция не периодична.Функция
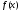 не существует при
не существует при 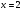 . Проверим гипотезу об асимптоте
. Проверим гипотезу об асимптоте 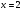 :
: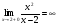
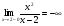
Таким образом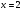 является вертикальной асимптотой данной функции
является вертикальной асимптотой данной функции Проверим гипотезу о существовании горизонтальной асимптоты:
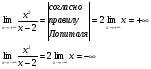
Отсюда следует, что горизонтальные асимптоты отсутствуют.Проверим гипотезу о существовании наклонной асимптоты:
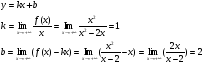
аналогично при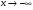
Таким образом, наклонная асимптота имеет вид: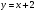
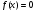 единственно при
единственно при 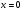 , и не существует при
, и не существует при 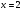 Исследуем знаки постоянства функции:
Исследуем знаки постоянства функции:
на промежутке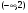
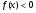
на промежутке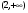
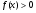
Исследуем функцию на монотонность:
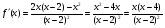 ;
;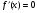 при
при 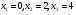
На интервале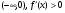 - функция возрастает
- функция возрастает
На интервале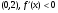 - функция убывает
- функция убывает
На интервале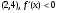 - функция убывает
- функция убывает
На интервале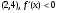 - функция убывает
- функция убывает
На интервале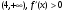 -функция возрастает
-функция возрастает
Точки экстремума: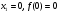 - локальный максимум
- локальный максимум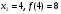 - локальный минимум
- локальный минимумИсследуем функцию на выпуклость:
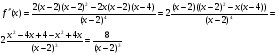
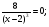 данное уравнение корней не имеет;
данное уравнение корней не имеет;
Производная второго порядка не существует при 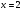
На промежутке 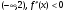 - функция выпукла вверх
- функция выпукла вверх
На промежутке 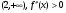 - функция выпукла вниз
- функция выпукла вниз
Таким образом, учитывая все вышеуказанное, эскиз графика функции будет выглядеть следующим образом:
y=x+2
x=2
0
4
8
y = f(x)
y = f(x)
X
Y
Найти локальные экстремумы функции
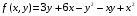
Найдем первые производные: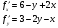
Составим систему:
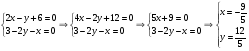
Найдем вторые производные:
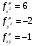
Поскольку производные 2-го порядка для данной функции не существуют, то вопрос о локальных экстремумах остается открытым.
Определить экстремумы функции
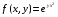 , если у2+2х2=12, х>0, у>0
, если у2+2х2=12, х>0, у>0
Составляем функцию Лагранжа:
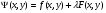
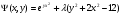
Найдем первые частные производные функции Лагранжа:
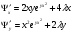
Составим систему уравнений:
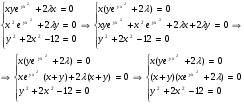
По условию: х>0, у>0
Таким образом: х = у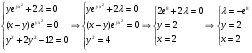
Определи вторые производные функции Лагранжа:
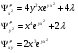
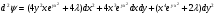
Учитывая значения переменных, полученные в п.3, имеем:
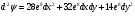
Найдем производные условной функции:
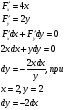
Таким образом:
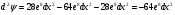
Видим, что в точке (2,2) исходная функция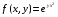 при условии у2+2х2=12, х>0, у>0, будет иметь строгий условный максимум, при этом
при условии у2+2х2=12, х>0, у>0, будет иметь строгий условный максимум, при этом 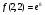
3. Интегральное исчисление функции одного переменного
1-3 Найти неопределенный интеграл:
а. 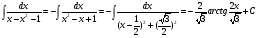
б. 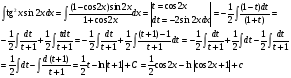
в. 
4 Вычислить 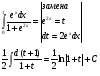
Таким образом: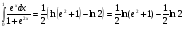
5. Определить площадь плоской фигуры, ограниченной кривыми
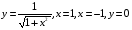
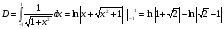

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ