Производная в задачах ЕГЭ. Задача В9, 11 класс
МОУ "Гимназия "Дмитров""
Московская область
г. Дмитров
Конспект урока по математике в 11 классе
"Производная в задачах ЕГЭ. Задача В9"
подготовила учитель математики
Сергеева Ирина Анатольевна
Дмитров, 2013
ЦЕЛИ УРОКА:
Учебные:
Повторить теоретические сведения по теме, необходимые для решения рассматриваемых задач.
Обобщить, закрепить и углубить имеющиеся знания по теме «Производная».
Научить применять полученные теоретические знания при решении различного типа математических задач.
Подготовка к ЕГЭ. Разработка рекомендаций к системе подготовки по решению задач типа В9.
Воспитательные:
Обучение навыкам: планирования деятельности, работы в оптимальном темпе, работы в группах, подведения итогов.
Развитие умения оценивать свои способности, свое положение в паре, умение контактировать с товарищами.
Воспитывать чувства ответственности и сопереживания.
Способствовать воспитанию умения работать в команде; умения критически относиться к мнению одноклассников.
Развивающие:
Развивать у учащихся умение находить нужную справочную литературу, самостоятельно добывать знания, учить самодиагностике.
Учить формированию ключевых понятий изучаемой темы.
Развитие исследовательских навыков. Развитие умения анализировать, систематизировать, интерпретировать полученные результаты.
Тип урока: комбинированный: обобщение, закрепление навыков применения свойств элементарных функций, применение уже сформированных знаний, умений и навыков применения производной в нестандартных ситуациях.
Оборудование: компьютер, проектор, экран, раздаточный материал.
Ход Урока:
1. Вступительное слово учителя: (3 мин)
«Помимо проблемы итоговой аттестации (решение задач В9, В15) возникают вопросы и сомнения, в какой мере приобретаемые в этой области знания могут и будут востребованы в дальнейшем».
Зачем нужна производная? Где мы встречаемся с производной и используем её? Можно ли без нее обойтись в математике и не только?
Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д., так как механический смысл производной - это мгновенная скорость.
При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Её решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления. Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И. Ньютона и Г.В. Лейбница, который использовал понятие бесконечно малой. Ньютон пришёл к открытию дифференциального исчисления при решении задач о скорости движения материальной точки в данный момент времени (мгновенной скорости).
2.Основная часть
Презентации учащихся
1 группа: "Геометрический смысл производной" (3 мин)
Работа в парах. (10 мин)
Решение задач 1 части раздаточного материала «Геометрический смысл производной», с дальнейшей самопроверкой.
1 часть. Геометрический смысл производной
1.

2.
3.

4.
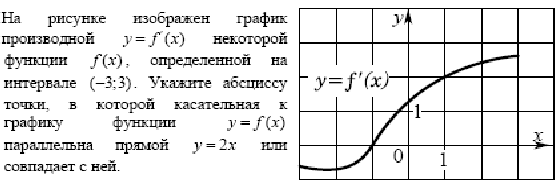
5.
6.
7.
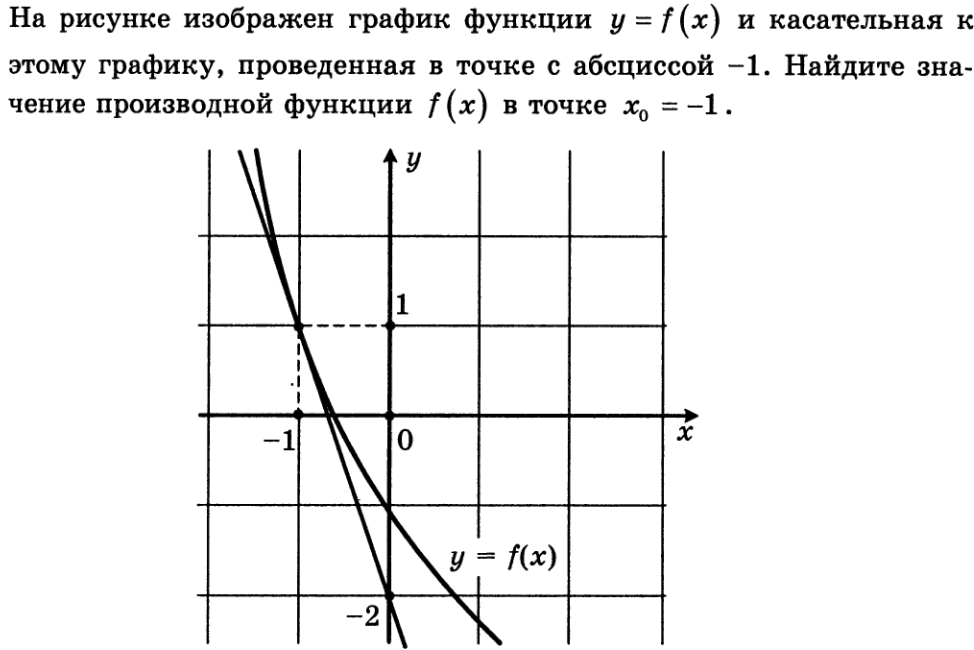
8.
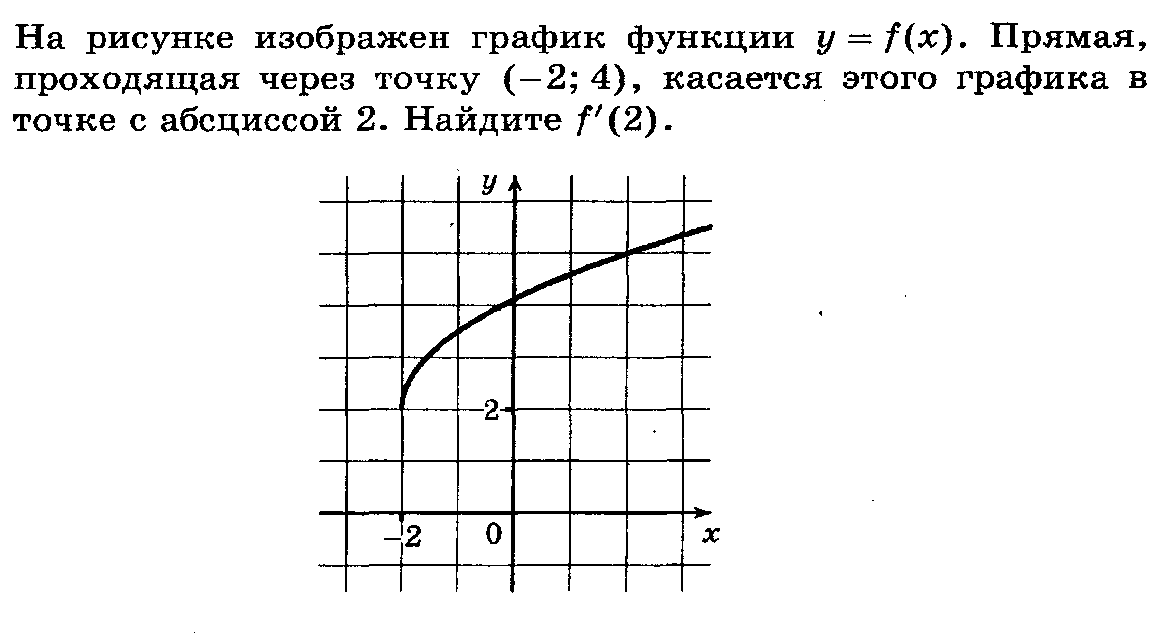
Зарядка для глаз (1 мин)
2 группа: "Применение производной к исследованию функции" (3 мин)
Решение задач 2 части раздаточного материала «Применение производной к исследованию функции», с дальнейшей самопроверкой. (15 мин)
2 часть. Применение производной к исследованию функций
1.

2.
3.
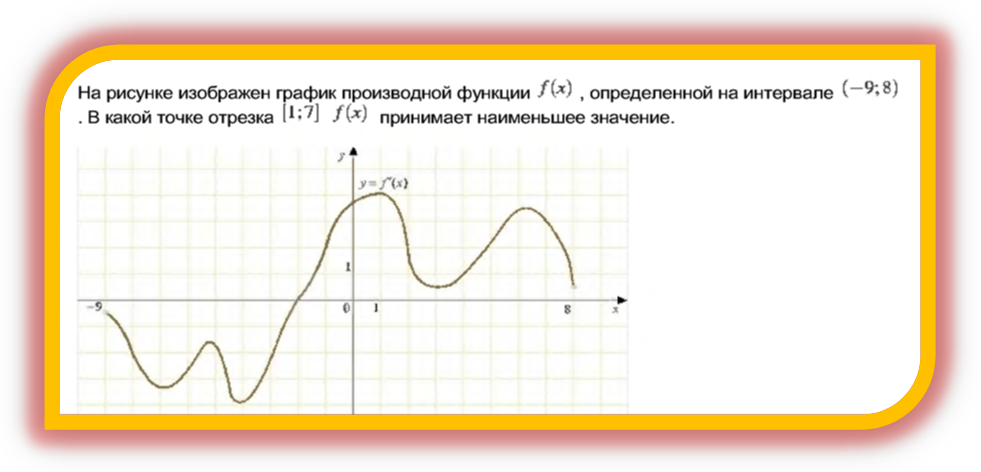
4.
5.
6.
7.
8.
3 группа: "Физический смысл производной" (3 мин)
Решение задач 3 части раздаточного материала «Физический смысл производной», с дальнейшей самопроверкой. (3 мин)
3 часть. Физический смысл производной
№1. Ребенок на санках в первые 4 с движения с горки проезжал расстояние, заданное формулой
![]() . Найдите его ускорение в момент времени t = 3 с.
. Найдите его ускорение в момент времени t = 3 с.
4 часть. (Рефлексия)
От каждой группы разработать и предоставить на уроке рекомендации (алгоритмы) к решения заданий типа В9, для создания сборника "В помощь выпускнику при сдаче ЕГЭ по математике".
1. На рисунке изображен график производной![]()
![]() . Что необходимо сделать, чтобы найти абсциссу точки, в которой касательная к графику функции
. Что необходимо сделать, чтобы найти абсциссу точки, в которой касательная к графику функции ![]() параллельна прямой y=kx+b (№1, геометрический смысл производной)
параллельна прямой y=kx+b (№1, геометрический смысл производной)
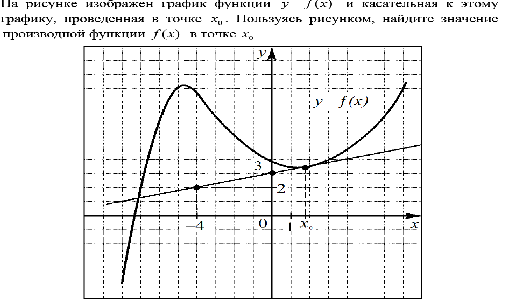
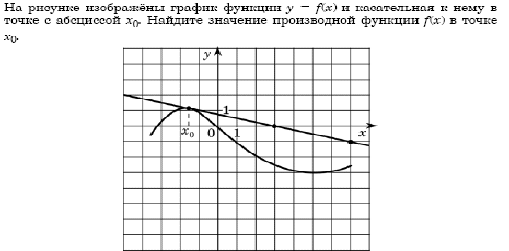
2. На рисунке изображен график функции ![]() и касательная к нему, в точке с абсциссой xо. Что необходимо сделать, чтобы найти значение производно функции
и касательная к нему, в точке с абсциссой xо. Что необходимо сделать, чтобы найти значение производно функции ![]() в точке xо. (№2, геометрический смысл производной)
в точке xо. (№2, геометрический смысл производной)
3. Дана функция ![]() и прямая y=kx+b, параллельная касательной к графику функции. Что необходимо сделать, чтобы не выполняя построений, найти абсциссу точки касания (№1, применение производной)
и прямая y=kx+b, параллельная касательной к графику функции. Что необходимо сделать, чтобы не выполняя построений, найти абсциссу точки касания (№1, применение производной)
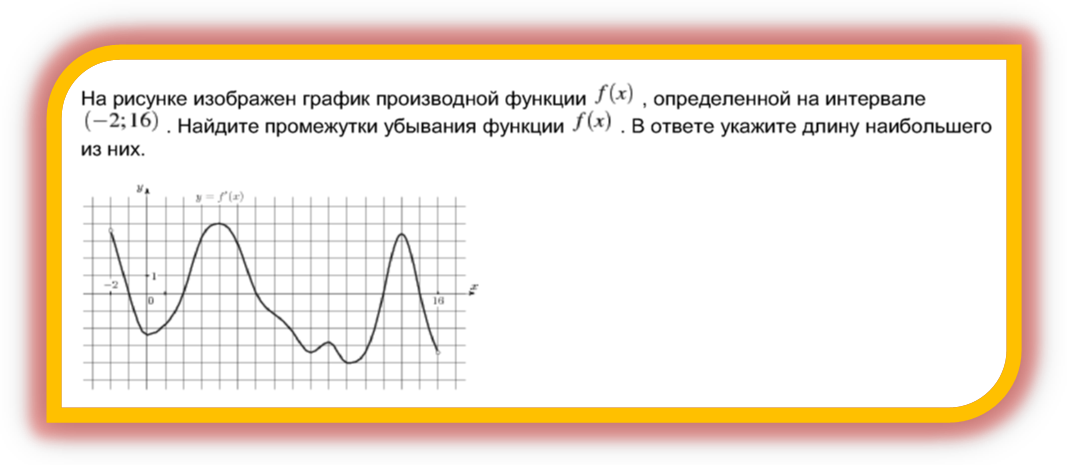
4. На рисунке изображен график производной ![]() . Сто необходимо сделать, чтобы найти промежутки убывания функции
. Сто необходимо сделать, чтобы найти промежутки убывания функции ![]() и в ответе указать длину наибольшего из них. (№3, применение производной)
и в ответе указать длину наибольшего из них. (№3, применение производной)
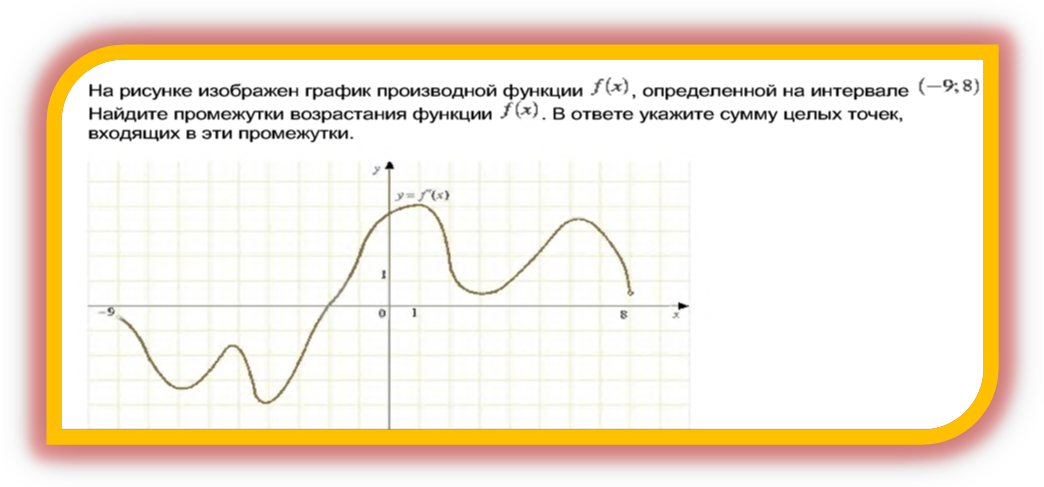
5. На рисунке изображен график производной ![]() . Что необходимо сделать, чтобы найти промежутки возрастания функции
. Что необходимо сделать, чтобы найти промежутки возрастания функции ![]() и в ответе указать сумму целых точек, входящих в эти промежутки (№4, применение производной)
и в ответе указать сумму целых точек, входящих в эти промежутки (№4, применение производной)
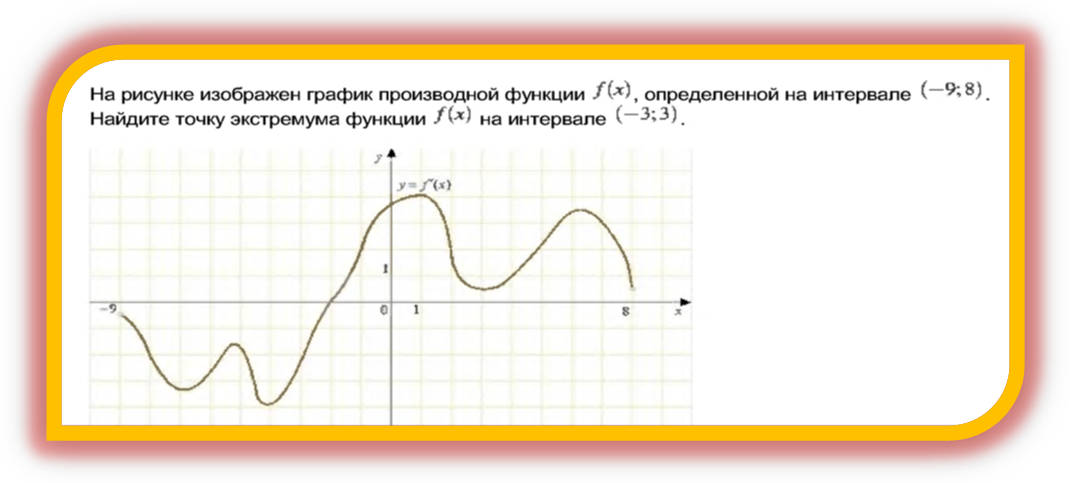
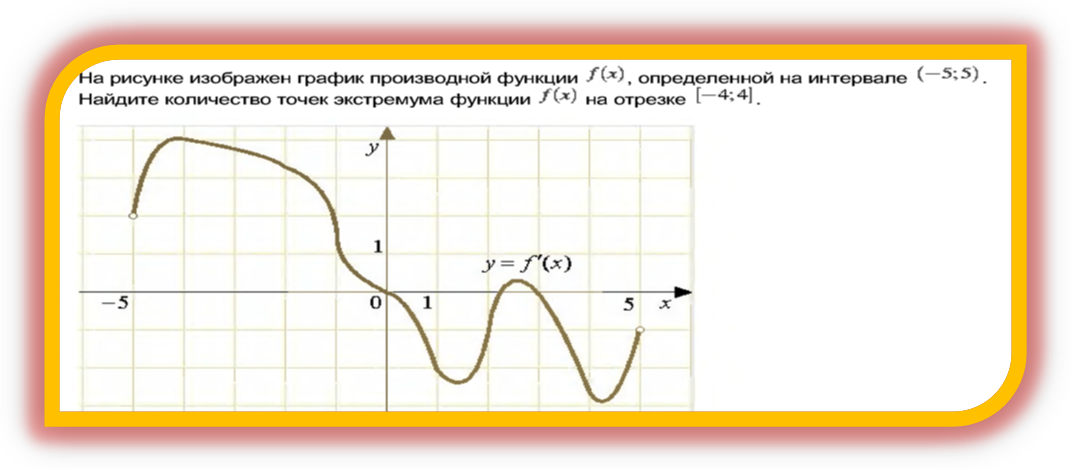
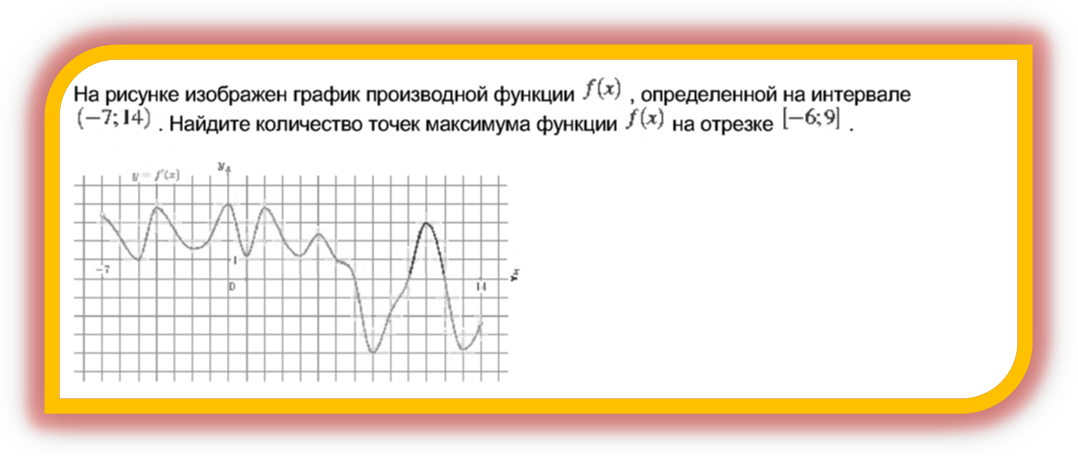
6. . На рисунке изображен график производной ![]() . Что необходимо сделать, чтобы найти точки экстремума и распознать их характер (№5, применение производной)
. Что необходимо сделать, чтобы найти точки экстремума и распознать их характер (№5, применение производной)
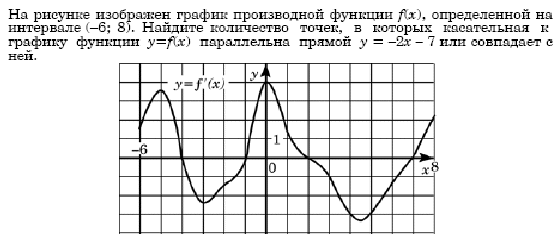
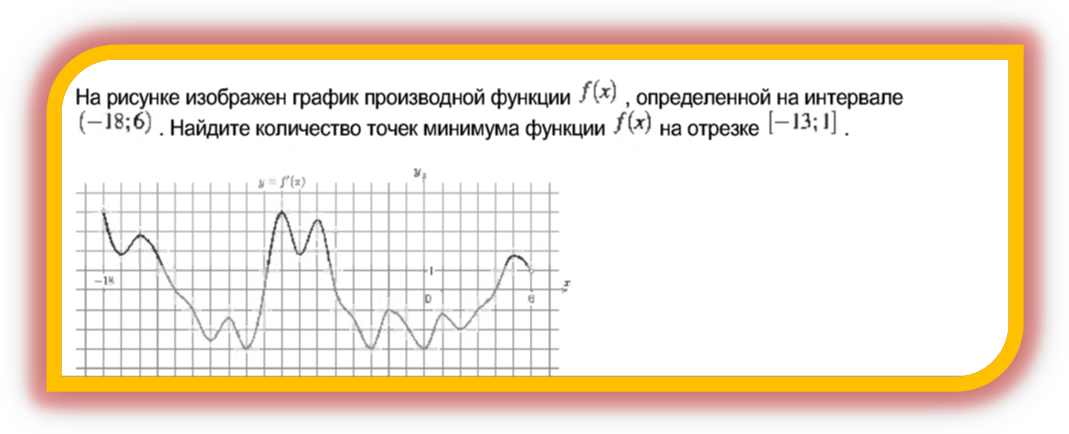
7. На рисунке изображен график производной ![]() . Что необходимо сделать, чтобы найти количество точек минимума (№7, применение производной)
. Что необходимо сделать, чтобы найти количество точек минимума (№7, применение производной)
8. На рисунке изображен график функции ![]() . Что необходимо сделать, чтобы определить количество целых точек, в которых производная
. Что необходимо сделать, чтобы определить количество целых точек, в которых производная ![]() отрицательна. (№9, применение производной)
отрицательна. (№9, применение производной)
9. Движение материальной точки задается формулой S(t). Что необходимо сделать, чтобы найти скорость материальной точки в момент времени t0. (№1, физический смысл производной)
10. Движение материальной точки задается формулой S(t). Что необходимо сделать, чтобы найти, в какой момент времени ускорение будет равно a0 . ((№1, физический смысл производной)
3. Решение задачи повышенного уровня сложности (если останется время)
Задача:
Найдите площадь треугольника, две вершины которого лежат на графике функции ![]() и имеют абсциссы 21 и -21, а третья вершинная является пересечением касательных, проведённых к графику данной функции в двух первых вершинах треугольника.
и имеют абсциссы 21 и -21, а третья вершинная является пересечением касательных, проведённых к графику данной функции в двух первых вершинах треугольника.
Решение:
1.Область определения функции задаётся неравенством ![]() , откуда получаем
, откуда получаем ![]() или
или ![]() .
.
2. При ![]() , функция принимает вид
, функция принимает вид ![]() ; найдём её производную
; найдём её производную ![]() , а также значения функции и производной в точке
, а также значения функции и производной в точке ![]() :
: ![]()
![]()
![]() . Используя полученные результаты, составим уравнение касательной
. Используя полученные результаты, составим уравнение касательной ![]() ;
;![]() .
.
3. При ![]() , функция принимает вид
, функция принимает вид ![]() ; найдём её производную
; найдём её производную ![]() , а также значения функции и производной в точке
, а также значения функции и производной в точке ![]() :
: ![]()
![]()
![]() . Уравнение касательной имеет вид
. Уравнение касательной имеет вид![]() .
.
4. Найдём абсциссу точки пересечения касательных. Для этого решим уравнение ![]() . Следовательно, ордината точки пересечения:
. Следовательно, ордината точки пересечения:![]() .
.
Таким образом, координаты вершин треугольника: A(-21;-24);
В(21;-24) и С(0;-8,25). Ординаты точек А и В равны, значит, сторона АВ параллельна оси абсцисс ОХ. Следовательно, высота треугольника, проведённая из вершины С: h=![]() . Тогда искомая площадь треугольника АВС:
. Тогда искомая площадь треугольника АВС: ![]()
4. Домашнее задание: Сборник Лысенко, стр. 211
№ 287,288,310
Используемая литература:
- Лысенко Ф.Ф Математика. Подготовка к ЕГЭ-2013 - Ростов-на-Дону, 2012
-Открытый банк задач ЕГЭ по математике

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ