Муниципальное казенное общеобразовательное учреждение средняя общеобразовательная школа с. Селезениха Кирово-Чепецкого района Кировской области

Рабочая образовательная программа

Курса по выбору

« Текстовые задачи на экзамене по математике »

(для учащихся 9 класса.)

Составила

Погонец Наталия Сергеевна

учитель математики

первой квалификационной категории

с.Селезениха - 2013

Пояснительная записка.

Умение решать задачи - практическое искусство, подобное плаванию, или катанию на коньках, или игре на фортепьяно: научиться этому можно, лишь подражая избранным образцам и постоянно тренируясь»...

Д. Пойа.

Курс по выбору для подготовки учащихся 9 классов к ГИА ,посвящен одной из самых трудных для ученика тем – решению текстовых задач.

В школьном курсе алгебры решению текстовых задач уделено катастрофически мало учебных часов. В то же время на выпускном экзамене в 9 классе предлагаются текстовые задачи различных уровней сложности и различных типов: на совместную работу, на движение, на планирование, на проценты, на зависимости между компонентами арифметических действий, и другие виды. Не малое место занимают текстовые задачи на вступительных экзаменах в ВУЗы, в ЕГЭ по математике, об этом следует помнить и готовиться к таким испытаниям заранее.

Текстовые задачи являются важным средством обучения математике. С их помощью учащиеся получают опыт работы с величинами, постигают взаимосвязи между ними, получают опыт применения математики к решению практических задач. Использование арифметических способов решения задач развивает смекалку и сообразительность, умение ставить вопросы, отвечать на них, то есть развивает естественный язык, готовит школьников к дальнейшему обучению. Арифметические способы решения текстовых задач позволяют развивать умение анализировать задачные ситуации, строить план решения с учетом взаимосвязей между известными и неизвестными величинами, истолковывать результат каждого действия в рамках условия задачи. Решение текстовых задач приучают детей к первым абстракциям, позволяют воспитывать логическую культуру, вызывая интерес сначала к процессу поиска решения задачи, а потом и к изучаемому предмету.

Текстовые алгебраические задачи представляют собой традиционный раздел элементарной математики. По своему содержанию текстовые задачи, как правило, тесно связаны с практической деятельностью человека и описывают некоторые реальные ситуации. Для решения обычно используется общая стандартная схема:

1. Анализ условий и выбор неизвестных величин, составление таблиц;

2. Составление уравнений и, возможно, неравенств;

3. Решение полученной системы, содержащей соотношения с искомыми неизвестными.

Данный курс способствует подготовке учащихся к продолжению обучения в профильном классе с математическим уклоном. Он расширяет базовый курс по математике, познакомит ребят с нестандартными, интересными подходами при решении текстовых задач, научит применять теорию на практике. Каждое занятие предлагаемого курса, а также все они в целом направлены на то, чтобы развить интерес школьников к предмету, познакомить их с общими идеями и методами, расширить представление об изучаемом в основном курсе материале, а главное - решать интересные задачи.

Умение решать ту или иную задачу зависит от многих факторов. Однако, прежде всего, необходимо научиться различать основные типы задач и уметь решать простейшие из них. В связи с этим целесообразно рассмотреть типовые задачи и их решения различными методами (с помощью уравнений, с помощью систем уравнений, логически и т. д.).

Программа курса рассчитана на 16 часов

Целью данного курса является подготовка к успешной сдаче экзамена и систематизации знаний учащихся с 5-9 класс

Курс призван

1. Систематизировать знания по решению текстовых задач;

2. Формировать независимость, гибкость и критичность мышления;

3. Развивать навыки по анализу текста, выделению главного, составлению плана и т.д.

Задачи курса:

• Познакомить учащихся с различными видами задач на «проценты», «движение», «работу», «числа», «сплавы», «смеси», с решением нестандартных задач.

• Выработать умения и навыки при решении текстовых задач и освоить каждый способ решения доведением до качеств, характеризуемых быстротой, легкостью, автоматизмом.

• Научить выполнять перенос математических идей и знаний на новые ситуации, на решение нестандартных задач; научить методам рассуждений - сравнения и аналогии, анализа и синтеза.

Занятия проводятся в форме обзорных лекций, на которых сообщаются теоретические факты, семинаров и практикумов по решению задач.

Виды организации работы: групповая, фронтальная, индивидуальная.

Требования к уровню подготовки обучающихся.

Учащиеся должны знать: алгоритм решения уравнений, формулу корней квадратного уравнения, дробно-рациональные уравнения, способы решения систем уравнений, пропорции и их свойства, приёмы рационального счета.

Учащиеся должны уметь: строить таблицы для каждого вида задач и уметь вносить в них данные задачи, решать линейные, квадратные, дробно-рациональные уравнения; системы уравнений первой и второй степени; выражать одно неизвестное через другое; заменять проценты дробью и наоборот; находить неизвестный член пропорции; выполнять действия с десятичными и обыкновенными дробями.

В результате изучения курса учащиеся должны:

Знать:

- виды текстовых задач;

- способы решения текстовых задач.

Уметь:

- исследовать текстовые задачи;

- записывать краткое условие задачи или строить таблицу по заданному условию;

- выбирать подходящее решение для данной текстовой задачи;

- решать простейшие текстовые задачи;

Содержание элективного курса.

Тема 1. Задачи на движение.

На первом занятии сообщаются цели и задачи курса, систематизируются знания учащихся об уравнениях и системах уравнений, о способах их решений.

В начале занятия рассмотреть:

• основные компоненты этого типа задач (время, скорость, расстояние);

• зависимость между этими величинами в формулах;

• план решения задач на движение (заполнение таблицы);

• обратить внимание на особенности при различных видах движения.

Затем рассматриваем решение задач этого типа.

Тема 2. Задачи на проценты.

Следует заметить, что задачи этого раздела входят как составная часть в решение других типовых задач. Заменяя проценты соответствующим количеством сотых долей числа, легко свести данную задачу на проценты к задаче на части. При решении задач данного типа предполагается использование калькулятора – всюду, где это целесообразно. Применение калькулятора снимает непринципиальные технические трудности, позволяет разобрать больше задач. Кроме того в ряде случаев необходимо считать устно. Для этого полезно знать некоторые факты, например: чтобы увеличить величину на 50%, достаточно прибавить ее половину; чтобы найти 20% величины, надо найти ее пятую часть; что 40% некоторой величины в 4 раза больше, чем ее 10%; что треть величины – это примерно 33% и т. д.

Важно, чтобы каждый ученик смог самостоятельно выбрать свой способ решения, наиболее ему удобный и понятный.

Тема 3. Задачи на смеси и сплавы.

Задачи, в которых идет речь о составлении сплавов, растворов или смесей двух или нескольких веществ. Все получающиеся сплавы или смеси однородны и при слиянии двух растворов объемы V₁иV₂,получается смесь, объем которой равен V₁+ V₂. Заметим, что такое допущение не всегда выполняется в действительности.

Тема 4. Задачи на совместную работу.

Основными компонентами задач этого типа являются:

а) работа А(выполненная, выполняемая или планируема к выполнению);

б) время Т (затраченное, используемое или необходимое для выполнения работы);

в) производительность труда N, т.е.работа, выполненная в единицу времени(фактическая или предполагаемая).

Указанные компоненты связаны между собой равенством N.

К задачам на работу относятся и задачи на «бассейны», в которых основными компонентами являются:

а) объем V бассейна;

б) время Т, необходимое для заполнения (или опорожнения) бассейна;

в) скорость Х наполнения бассейна.

Указанные компоненты связаны между собой равенством Х.

Тема 5. Решение нестандартных текстовых задач.

Исключение невозможных значений, подбор ответа, рекомендации по решению нестандартных задач, задачи на «числа»..

Тема 6. Разные задачи. Учащимся предлагаются для решения различные задачи.

Учебно-тематическое планирование элективного курса

№ п/п

Тема занятия

Количество часов

Форма проведения

1.

Задачи на движение.

3

Лекция, практика

2.

Задачи на проценты

2

Лекция, практика

3.

Задачи на смеси и сплавы

2

Лекция, практика

4.

 Промежуточный зачет.

1

Практикум

5.

Задачи на «работу».

2

Лекция, практика

6.

Решение нестандартных текстовых задач.

3

Лекция, практика

7.

Разные задачи

2

Урок-практикум

8.

Итоговая зачетная работа

1

Всего

16

Методические рекомендации

Занятие 1-3. Задачи на движение.

Широко известны серьезные трудности, которые испытывают учащиеся при решении задач.

Первая трудность состоит в составлении математической модели. Для того, чтобы перевести содержание задачи на математический язык, необходимо изучить и правильно истолковать его, формализовать вопрос задачи, выразив искомые величины через известные величины и введённые переменные.

Вторая трудность – составление уравнений и неравенств, связывающих данные величины и переменные, которые вводит учащийся.

Третья трудность состоит в том, чтобы составить функцию (отношение), применительно к которой формулируется вопрос задачи.

Четвертая трудность – решение полученного уравнения, системы уравнений или неравенств желательно наиболее рациональным методом.

Задача 1. Из пункта А в пункт В со скоростью 80 км/ч выехал первый автомобиль, а через некоторое врем с постоянной скоростью второй. После остановки на 20 мин в пункте В второй автомобиль поехал с той же скоростью назад. Через 48 км он встретил первый автомобиль, шедший навстречу, и был на расстоянии 120 км от В в тот момент, когда в пункт В прибыл первый автомобиль. Найти расстояние от А до места первой встречи автомобилей, если АВ=480 км.

Самое важное- это понять, что первая встреча автомобилей произошла в тот момент, когда второй автомобиль обгонял первый.

Если обозначить расстояние от А до места первой встречи через S км, а скорость второго автомобиля через V км/ч, то из условия задачи видно, что расстояние в 72 км (120-48=72) второй автомобиль пройдет за то же время, которое понадобится первому автомобилю, чтобы преодолеть 48 км. Следовательно, , откуда V = 120 км/ч

От места первой встречи до пункта В первому автомобилю оставалось пройти (480- S) км со скоростью 80 км/ч. На это он затратил (480- S)/80 ч. За это же время второй автомобиль прошел от места первой встречи до пунктаВ, потратил 1/3 ч на стоянку в пункте В и еще 120/ Vч на то, чтобы отъехать от В на 120 км. Таким образом, можно составить еще одно уравнение

.

Из него, зная, что V=120, находим S=160.

Задача 2. Перемещение двух тел по окружности в разных направлениях можно уподобить движению навстречу друг другу по прямой, даже если тела стартовали из одной точки вроде бы сразу разошлись, а не сблизились.

Два тела, двигаясь по окружности в одном и том же направлении, встречаются каждые 56 мин. Если бы они двигались с теми же скоростями в противоположных направлениях, то встречались бы каждые 8 мин.. Если при движении в противоположных направлениях в некоторый момент времени расстояние по окружности между телами 40м, то через 24с оно будет 26м. (в течение этих 24 с тела не встретятся). Найдите скорости тел и длину окружности.

Пусть с - длина окружности, х м/мин - скорость 1-го тела, у м/мин- скорость 2-го, х >у. При движении в одном направлении первое тело догоняет второе со скоростью (х – у)м/мин. После одного из обгонов следующий обгон имеет место через столько минут, сколько понадобится , чтобы преодолеть с метров со скоростью (х – у)м/мин, т.е. через 56 мин.

(1)

При движении в разных направлениях тела сближаются со скоростью (х + у)м/мин, причем с метров они вместе проходят за 8 минут.

(2)

Если первоначальное расстояние было равно 40 м, а осталось пройти до встречи 26м, то общий пройденный путь составляет 40м-26м=14м. Он был преодолен со скоростью (х+у) м/мин за 24с, т.е. за 2/5 мин.

(3)

Разделив уравнение 2 на 1,получим

,

Подставляя в уравнение 3 находим х=20, у=15, а из уравнения 2 получаем с=280.

Задачи для решения.

1. Пароход, отчалив от пристани А, спустился вниз по течению реки на 60 км до устья впадающего в нее притока и поднялся вверх по притоку (против течения) на 20 км до пристани В, Весь путь от А до В пароход прошел за 7 часов. Скорость течения реки и скорость течения притока равны 1 км/ч. Найти собственную скорость парохода (собственная скорость— скорость в неподвижной воде).

Ответ.11км/ч.

2. В соревнованиях по бегу на дистанцию 120 м участвуют три бегуна. Скорость первого из них на 1 м/с больше скорости второго, а скорость второго бегуна равна полусумме скоростей первого и третьего. Определить скорость третьего бегуна, если известно, что первый бегун пробежал дистанцию на 3 с быстрее третьего.

Ответ.8м/с.

3. Из пункта А в пункт В вышел пешеход. Одновременно с ним из пункта В в пункт А выехал велосипедист, который встретил пешехода через 50 мин после своего выезда из В. Сколько времени потребовалось бы пешеходу, для того чтобы пройти весь путь из Л в В, если известно, что велосипедист проделал бы тот же путь на 4 часа быстрее пешехода?
Ответ.5часов.

4. От пристани А к пристани В против течения реки отошел катер, собственная скорость которого В стоячей воде в 7 раз больше скорости течения реки. Одновременно навстречу ему от пристани В, расстояние которой до А по реке равно 20 км, отошла лодка. На каком расстоянии от В произошла встреча катера. с лодкой, если известно, что через полчаса посла начала движения лодке оставалось проплыть 4 км до'; встречи и что катер затратил на весь путь до Е;стречи с лодкой на 20 мин больше, чем на путь от места встречи до пункта В?
Ответ.8км.

5. В гору ехал автомобиль. В первую секунду после достижения пункта А он проехал 30 м, а в каждую следующую секунду он проезжал на 2 м меньше, чем в предыдущую. Через 9 с после того, как автомобиль достиг пункта А, навстречу ему выехал автобус из пункта В, находящегося на расстоянии 258 м от пункта А. В первую секунду автобус проехал 2 м, а в каждую следующую секунду он проезжал на I м больше, чем в предыдущую. Какое расстояние проехал автобус до встречи с автомобилем?

Ответ.20м.

6. Станции А, В и С находятся на одной и той же железной дороге, причем расстояние от В до С равно 200 км. Известно, что скорый поезд, вышедший из Л, и пассажирский поезд, вышедший одновременно с ним из С, встретились на станции В. Найти расстояние между станциями А и С, если оно меньше 300 км, а скорый поезд идет в 1,5 раза быстрее, чем пассажирский.

Ответ.100км.

7. Два лыжника стартовали на дистанции 10 км друг за другом с интервалом в 6 мин. Второй лыжник догнал первого в двух километрах от точки старта. Дойдя до поворота на отметке 5 км, второй лыжник повернул обратно и встретил первого на расстоянии 1 км от точки поворота. Найти скорость первого лыжника.

Ответ.10км/ч.
8. Лодка плывет вчетверо медленнее катера, при этом 16км катер проплывает быстрее лодки на 3 часа. Найдите скорость лодки.

Ответ.4км/ч.

9.Петя вышел из школы и пошел домой со скоростью 4,5 км/ч. Через 20 мин по той же дороге из школы выехал Вася на велосипеде со скоростью 12км/ч. На каком расстоянии от школы Вася догонит Петю.

Ответ.2,4км.

Занятие 4-5. Задачи на проценты.

Проценты употребляются для сравнения однородных положительных количеств. Один процент это одна сотая: 1%=1/100, соответственно р% = р/100.

Один процент от количества А- это одна сотая часть количества А: 1% от А равен 1/100 А, р% от А равен А*р/100. Процентом р задается коэффициент к=р/100.

Вычисление количеств по процентам. Дано количество А и некоторый процент р. Требуется найти количество, которое этот процент выражает: Ар/100

Вычисление процентов по количеству. Сколько процентов составляет А от В: (А/В)*100%

Каково количество, р% от которого есть А: (100/р)*А

Каково количество, большее чем А на р%: (1+ р/100)*А

Каково количество, меньшее чем А на р%: (1- р/100)*А

На сколько процентов А больше чем В : .

Задача 1. Находясь в гостях у кролика, Вини-Пух за первые 3 часа съел 40% всего запаса меда кролика. Пятачок и кролик вместе, за это же время, съели 300 граммов меда. За следующие 3 часа Вини-Пух съел 2/3 оставшегося меда, а пятачок и кролик съели 100г меда на двоих, после чего у кролика осталось 1,6 кг меда. Сколько меда было у кролика до визита Вини-Пуха?

Пусть первоначально у кролика было х кг меда. Вини-Пух съел 1 раз 0,4х кг, а Пятачок и кролик съели 300г мёда. У кролика осталось х-0,4х-0,3=0,6х-0,3

Вини-Пух съел второй раз 2/3(0,6х-0,3)=0,4х-0,2, а Пятачок и кролик 100г. У кролика осталось 0,6х-0,3-0,4х+0,2-0,1=0,2х-0,2.Зная, что осталось 1,6кг ,составим уравнение: 0,2х-0,2=1,6 х=9

Задача 2. Длина дистанции трех дневной велогонки была 480 км. В первый день велогонщики проехали 25% всего пути, а во второй день 55% оставшегося пути . Сколько километров проехали велогонщики в третий день пути?

В 1-ый день проехали км

Оставшийся путь составил 480-120=360 км. Тогда во второй день велогонщики проехали км. В третий день велогонщики проехали 360-198=162км.

Задача 3. В одном городе Канады 70% жителей знают французский язык и 80%- английский язык. Сколько процентов жителей этого города знают оба языка.

Исходим из того, что каждый житель города знает хотя бы один из двух языков. Пусть х жителей знают только английский язык, у- только французский, с- оба языка.

, .

Сложив оба эти равенства получим : .

Задача 4. Капитал в 1300 рублей отдан в рост на 2,5 года по 6%. Сколько прибыли (процентных денег) получено с капитала?

1. 6%- это годовые проценты, найдем срочные проценты, т.е. проценты за 2,5 года. Срочные проценты равны 6%* 2,5=15%

15% прибыли составляют 15/100 части капитала. С капитала в 1300 рублей прибыли за 2,5 года будет получено: 1300 * 15/100=195 руб.

2. 2. То, что капитал был в обороте по 6%, значит что 6коп. процентных денег получено будет в 1 год с 1 рубля капитала. Найдем процентные деньги с 1рубля за 2,5 года. 6 *2,5 =15 коп. С капитала 1300 руб. процентных денег получено будет: 15 * 1300=195 руб.

Задачи для решения.

1.В начале года в сберкассу на книжку было положено 1640 руб. и в конце года было взято обратно 882 руб. Еще через год на книжке снова оказалось 882 руб. Сколько процентов начисляет сберкасса в год?
Ответ. 5%.

2.По оценке социологов за период в 24 года — с 1966 г. по 1989 г. включительно — в городе N должно было быть заключено 3150 браков. Фактически в 1966 г. состоялось ЮО.браков. Каждый последующий год заключалось на 5 браков больше, чем в предыдущий, пока не была досрочно, причем за целое число лет, достигнута предварительная оценка — 3150 браков. После этого, вплоть до конца 1989 г., годовое число вступлений в брак сократилось на 11 по сравнению с годом достижения оценки. На сколько процентов реальное число браков за 24 года превысило предварительную оценку?
Ответ. На 18%. 98

3. В сообщении о реконструкции цеха указано, что в результате реконструкции процент высвободившихся рабочих заключен в пределах от 1,7 до 2,3%. Определить минимально возможное число рабочих, первоначально занятых в цехе. Ответ.44.

4.Какой процент ежегодного дохода давал банк, если положив на счет 13000 рублей, вкладчик через 2 года получил 15730 рублей?

Ответ.10%

5.Денежный вклад в банк за год увеличивается на 11 %. Вкладчик внес в банк 7000 рублей. В конце первого года он решил увеличить сумму вклада и продлить срок действия договора еще на год, чтобы в конце второго года иметь на счету не менее 10000 рублей. Какую наименьшую сумму необходимо дополнительно положить на счет по окончании первого года, чтобы при той же процентной ставке (11 %) реализовать этот план? (Ответ округлите до целых.)

Ответ.1240

6. В осеннее – зимний период цена на фрукты возрастала трижды: на 10%, на 20%, и на 25%. На сколько процентов возросла зимняя цена по сравнению с летней?

Ответ.65%

7.Хлебопекарня увеличила выпуск продукции на 50%. На сколько процентов увеличится прибыль пекарни, если отпускная цена ее продукции возросла не 10%, а ее себестоимость для пекарни, которая до этого составляла ¾ отпускной цены, увеличилась на 20%.

Ответ.20%

8. На первом поле 65% площади занято овсом. На втором поле овсом занято 45% площади. Известно, что на первом и втором полях вместе под овсом занято 53% общей площади. Какую часть всей засеянной площади составляет первое поле?

Ответ.2/5

9. Число 51,2 трижды увеличили на одно и то же число процентов, а затем трижды уменьшили на то же самое число процентов, в результате получили число 21,6. На сколько процентов увеличивали, а затем уменьшали это число?

Ответ.10%

Занятие 6-7. Задачи на смеси и сплавы

Задачи на смеси и сплавы вызывают наибольшие затруднения у школьников. В процессе решения каждой такой задачи целесообразно действовать по следующей схеме.

1. Изучение условия задачи. Выбор неизвестных величин (их обозначаем буквами х, у и т.д.), относительно которых составляем пропорции. Выбирая неизвестные параметры, мы создаем математическую модель ситуации, описанной в условии задачи.

2. Поиск плана решения. Используя условия задачи, определяем все взаимосвязи между данными величинами.

3. Осуществление плана, т.е. оформление найденного решения – переход от словесной формулировки к составлению математической модели.

4. Изучение полученного решения, критический анализ результата.

При решении задач на смеси часто путают проценты и доли, раствор и растворенное вещество. Необходимо помнить, что массовая доля находится делением значения процентной концентрации на 100%, а масса растворенного вещества m(в-ва) равна произведению массы раствора m(р-ра) на массовую долю:

m(в-ва) = m(р-ра)•.

В большинстве случаев задачи на смеси и сплавы становятся нагляднее, если при их решении использовать схемы, иллюстративные рисунки или вспомогательные таблицы.

Задача 1. В каких пропорциях нужно смешать а%-й и b%-й растворы кислоты (a < b), чтобы получить с%-й раствор?

Возьмем х г а%-го раствора и у г b%-го раствора кислоты. Составим таблицу:

Kонцентрация раствора,
%

Масса раствора,
г

Масса кислоты,
г

a

х

0,01ax

b

у

0,01by

c (смесь)

x + y

0,01c(x + y)

Составим и решим уравнение:

0,01ах + 0,01by = 0,01c(x + y),

(b – с)у = (с – а)х,

x : у = (b – с) : (с – а).

Воспользуемся диагональной схемой:

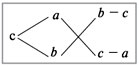
В этой схеме а и b – концентрации исходных растворов, с – требуемая концентрация кислоты в процентах, а «крест-накрест» – записаны их разности (b – с) и (с – а), соответствующие отношению масс растворов а и b.

Задача 2. Сколько по массе 90%-го и 60%-го растворов фосфорной кислоты надо взять, чтобы получить 5,4 кг 80%-го раствора фосфорной кислоты?

Решение: Составим диагональную схему:

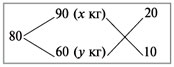
Получаем:

х : у = 20 : 10 = 2 : 1.

Значит, 90%-го раствора фосфорной кислоты надо взять в 2 раза больше, чем 60%-го, т.е. х = 2y.

Составим уравнение: 2y + y = 5,4.

Отсюда y = 1,8 кг.

Ответ. 3,6 кг 90%-го и 1,8 кг 60%-го растворов фосфорной кислоты.

Задача 3. Сплавили два слитка серебра: 75 г 600-й и 150 г 864-й пробы. Определить пробу сплава.

Решение: Пусть проба сплава равна х.

Составим диагональную схему:

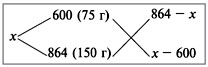
Получаем:

(864 – х) : (х – 600) = 75 : 150 = 1 : 2;

1728 – 2х = х – 600; х = 776.

Ответ. Получили сплав 776-й пробы.

Задача 4. Смешали некоторые количества 72%-го и 58%-го растворов кислоты, в результате получили 62%-й раствор той же кислоты. Если бы каждого раствора было взято на 15 л больше, то получился бы 63,25%-й раствор. Сколько литров каждого раствора было взято первоначально для составления первой смеси?

Решение: Дважды используем диагональную схему:

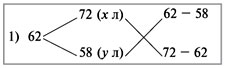
Получаем: х : у = 4 : 10 = 2 : 5.

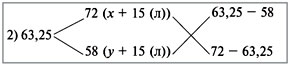
Получаем: (х + 15) : (y + 15) = 5,25 : 8,75 = 3 : 5.

Составим систему уравнений и решим ее:

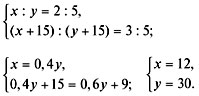
Ответ. В первой смеси было 12 л 72%-го раствора и 30 л 58%-го раствора.

Задача 5. Сколько граммов 9%-го раствора спирта можно получить из 200 г 70%-го раствора спирта?

Решение: 9%-й раствор спирта получают из 70%-го, разбавляя его водой. В воде 0% спирта. Применим диагональную схему:

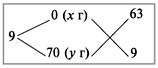
Получаем: х : у = 63 : 9 = 7 : 1.

Значит, 1 часть 70%-го раствора спирта надо разбавить 7 частями воды. Поэтому 200 г 70%-го раствора спирта надо разбавить 200•7 = 1400 г воды.

Всего получим: 200 + 1400 = 1600 г 9%-го раствора спирта.

Ответ. Из 200 г 70%-го раствора спирта можно
получить 1 кг 600 г 9%-го раствора спирта.

Задачи для решения.

1. Сплавляя два одинаковых по весу куска чугуна с разным содержанием хрома, получили сплав, в котором содержалось 12 кг хрома. Если бы первый кусок был в два раза тяжелее, то в сплаве содержалось бы 16 кг хрома. Известно, что процентное содержание хрома в первом куске на 5% меньше, чем во втором. Найти процентное содержание хрома в каждом куске чугуна.

2. Смешали 300 г 60%-ного раствора серной кислоты и 200 г 80%-ного раствора серной кислоты. Сколько процентов серной кислоты в получившемся растворе?

3. Имеется два сплава. Один содержит 2,8 кг золота и 1,2 кг примесей, другой — 2,7 кг золота и 0,3 кг примесей. Отрезав по куску от каждого сплава и сплавив их, получили 2 кг сплава с процентным содержанием золота 85%. Сколько килограммов металла отрезали от второго сплава?

4. Отношение массы олова к массе свинца в куске сплава равно 2:3. Этот кусок сплавили с куском олова весом 3 кг и получили новый сплав с процентным содержанием свинца 10%. Найдите массу олова в новом сплаве.

5. Имеются два слитка сплава олова медью. Первый слиток содержит 230 г олова и 20 г меди, а второй слиток — 240 г олова и 60 г меди. От каждого слитка отрубили по куску, сплавили их и получили 300 г сплава. Сколько граммов отрубили от первого слитка, если в полученном сплаве было 84% олова?

6. В двух одинаковых сосудах находятся растворы серной кислоты концентрации 28,7% и 37,3%. Растворы сливают. Какова концентрация полученного раствора кислоты?

7. У ювелира два одинаковых по массе слитка, в одном из которых 36% золота, а в другом 64%. Сколько процентов золота содержится в сплаве, полученном из этих слитков?

8. У кузнеца имеется два одинаковых по массе бронзовых бруска. В одном олово состав­ляет 43% массы, а в другом медь составляет 43% массы. Сколько процентов олова будет содержать сплав, полученный при переплавке этих брусков?

9. Для размножения водорослей вода в аквариуме должна содержать 2% морской соли. Сколько литров пресной воды нужно добавить к 80 л морской воды с 5%-ым содержанием соли, чтобы получить воду, пригодную для заполнения аквариума?

Занятие 8. Промежуточный зачет

Смысл профильного курса заключается в предоставлении каждому ученику «индивидуальной зоны потенциального развития», поэтому – нельзя требовать от каждого ученика твердого усвоения каждой темы. Специальный зачет или экзамен по курсу не предусмотрен, но предлагаются некоторые варианты выполнения учениками зачетных заданий:

1. Решение учеником в качестве индивидуального домашнего задания предложенных учителем задач из того списка, что завершает каждый модуль. Подбор индивидуальных заданий осуществляется с учетом уровневой дифференциации, причем выбор делают сами ученики, оценивая свои возможности и планируя перспективу развития.

2. Решение группой учащихся в качестве домашнего задания предложенных учителем задач из того же раздела. Работа в группе способствует проявлению интереса к учению как деятельности.

Занятие 9-10. Задачи на «работу».

Основными компонентами задач этого типа являются:

а) работа А(выполненная, выполняемая или планируема к выполнению);

б) время Т(затраченное, используемое или необходимое для выполнения работы);

в) производительность труда N, т.е.работа, выполненная в единицу времени(фактическая или предполагаемая).

Указанные компоненты связаны между собой равенством N.

К задачам на работу относятся и задачи на «бассейны», в которых основными компонентами являются:

а) объем V бассейна;

б) время Т, необходимое для заполнения (или опорожнения) бассейна;

в) скорость Х наполнения бассейна.

Указанные компоненты связаны между собой равенством Х.

Задача 1. По плану тракторная бригада должна была вспахать поле за 14дней. Бригада вспахивала ежедневно на 5 га больше, чем намечалось по плану, и потому закончила пахоту за 12 дней. Сколько гектаров было вспахано? Найдите площадь поля.

Речь идет о процессе работы.

Величины

процессы

по плану

фактически

А га

Апл-?

Аф-?

N га/день

Nпл

Nф на 5 га/день больше, чем Nпл.

Т дни

14

12

х- производительность бригады по плану,

(х+5)- фактическая производительность бригады

Апл=х * 14 (га), Аф=(х+5) * 12 (га). По условию площадь поля в обоих случаях одинакова.

14х=12(х+5), 2х=60, х=30

Производительность бригады по плану- 30 га/день. Площадь поля 14 * 30 =420 га.

Задачи для решения.

1.В бассейн проведены две трубы, подающая и отводящая, причем через первую бассейн наполняется на 2 часа дольше, чем через вторую опорожняется. При заполненном на 1/3 бассейне были открыты обе трубы, и бассейн оказался пустым спустя 8 часов. За сколько часов, действуя отдельно, первая труба наполнит, а вторая опорожнит бассейн?

2. К двум бассейнам подведены две трубы разного диаметра (к каждому бассейну своя труба). Через первую трубу налили в первый бассейн определенный объем воды и сразу после этого во второй бассейн через вторую трубу налили такой же объем воды, причем на все это вместе ушло 16 часов. Если бы через первую трубу вода текла столько времени, сколько через вторую, а через вторую трубу — столько времени, сколько через первую, то через первую трубу налилось бы воды на 320 м3 меньше, чем через вторую. Если бы через первую трубу проходило на 10 м3/ч меньше, а через вторую — на 10 м3/ч больше воды, то, чтобы налить в бассейн (сначала в первый, а потом во второй) первоначальные объемы воды, ушло бы 20 часов. Сколько времени лилась вода через каждую из труб?

Ответ.10часов,6часов.

3. В бассейн проведены четыре трубы. Когда открыты первая, вторая и третья, бассейн наполняется за 12 мин; когда открыты вторая и четвертая трубы - за 15 мин; когда открыты только первая, третья и четвертая трубы - за 20 мин. За какое время наполнится бассейн, если открыты все четыре трубы?

4. При одновременной работе двух насосов пруд был очищен за 2 ч 55 мин. За сколько времени мог бы очистить пруд каждый насос, работая отдельно, если один из них может эту работу выполнить на 2 ч быстрее другого?

5. Два рабочих выполнили всю работу за 10 дней, причем последние два дня первый из них не работал. За сколько дней первый рабочий выполнил бы всю работу, если известно, что за первые семь дней они вместе выполнили 80% всей работы?

6. В бассейн проведены три трубы. Одна первая труба наполняет бассейн в 2,6 раза быстрее, чем одна вторая труба, а одна вторая труба наполняет бассейн на 3 ч медленнее, чем одна третья труба. За сколько часов одна третья труба наполняет бассейн, если все три трубы, работая одновременно, наполняют бассейн за 3 ч 45 мин.

Ответ.15часов.

7.Две машинистки могут перепечатать рукопись за 6 ч. После 5 часов совместной работы вторая машинистка продолжила работу самостоятельно и завершила ее за 3 часа. За какое время каждая машинистка сможет перепечатать рукопись?

Ответ.9, 18 часов

8. Две бригады землекопов вырыли по одинаковому котловану, вторая бригада работала на полчаса больше первой. Если бы в первой бригаде было на 5 человек больше, то она могла бы закончить работу на 2ч раньше. Определить число землекопов в каждой бригаде, если производительность у всех одинакова.

Ответ: 25, 24

Занятие 11-13. Решение нестандартных задач.

Под нестандартной задачей мы будем понимать задачу, алгоритм решения которой учащемуся не известен, нужен самостоятельный поиск ключевой идеи. Познакомить учащихся методом полного перебора, исключением невозможных.

Задача 1.На шахматной доске 8х8 стоит 31 пешка. Доказать, что найдется уголок из трех клеток, на котором не стоит пешка.

Доска очень большая. Уменьшим её до размеров 2х2 и прикинем сколько там должно быть пешек, чтобы задача имела решение. Сформулирована похожая задача: На шахматной доске 2х2 стоит 1 пешка. Доказать, что найдется уголок из трех клеток, на котором не стоит пешка. Доказательство сводится к перебору 4-х вариантов. Попробуем найти на большой доске маленькую доску. Для этого разобьём большую доску на кусочки 2х2. Таких кусочков будет 16, но всего пешек 31. Если в каждый квадрат мы будем ставить по 2 пешки, то их не хватит. В один из таких квадратиков придется поставить 1 пешку, это обеспечит существование искомого варианта.

Задача 2. Существует ли десятизначное число, делящееся на 11, в записи которого использованы все цифры от 0 до 9?

Число делится на 11, если разность суммы цифр, стоящих на нечетных местах и суммы цифр, стоящих на четных местах, делится на 11.

Запишем цифры по убыванию, тогда у полученного числа 9876543210 эта разность равна пяти. Поменяем местами 5 и 8.Первая сумма увеличится на 3, а вторая уменьшится на 3. Их разность станет равна 11. Число 9576843210 делится на 11.

Задача 3. Можно ли в центры клеток шахматной доски 8х8 вбить 16 гвоздей так, чтобы никакие три гвоздя не лежали на одной прямой.

1. Да. Возможный вариант:

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

Задачи для решения.

1. Расставьте по кругу четыре нуля, три единицы и три двойки так, чтобы сумма любых трех подряд идущих чисел не делилась на три.

2. 4 черные коровы и 3 рыжие дают за 5 дней столько молока, сколько 3 черные коровы и 5 рыжих дают за 4 дня. У каких коров удои больше: у черных или у рыжих?

Ответ. у рыжих коров удои больше.

3. Найдите последнюю цифру числа 8^2003

Ответ. Так как 2003= 500 * 4 +3, то 8^2003 оканчивается той же цифрой, что и 8^3, то есть 2

3. Докажите, что если в числе 12008 между нулями вставить любое количество троек, то получится число, делящееся на 19.

5. На столе лежат в ряд четыре фигуры: треугольник, круг, прямоугольник и ромб. Они окрашены в разные цвета: красный, синий, желтый, зеленый. Известно, что красная фигура лежит между синей и зеленой; справа от желтой фигуры лежит ромб. Круг лежит правее и треугольника и ромба; треугольник лежит не с краю; синяя и желтая фигуры лежат не рядом. Определите, в каком порядке лежат фигуры и какого они цвета.

Ответ. Прямоугольник желтый, ромб зеленый, треугольник красный, квадрат синий.

6. У Пети есть полная 12-ти литровая канистра бензина и две пустые: 8- литровая и 5-литровая. Как ему разделить бензин на 2 равные части?

7. Человек в лодке начал грести против течеввя быстрой реки. Однако через 4 мин лодка оказалась на 80 м шже по течению. Развернув ее, он перестал грести, иг пока он отдыхал, лодку снесло на 40 м. Затем он принялся грести по течению, причем лодка двигалась относительно воды с той же скоростью, как и в первые 4 мин, и прошла еще 40 м. В целом после разворота лодки прошло 100 секунд. Какова скорость течения реки?

Ответ. 40 м/мин.

8. В классе присутствуют учитель и несколько учеников. Найти число учеников, если известно, что возраст учителя на 24 года больше среднего возраста учеников и на 20 лет больше среднего возраста всех присутствующих в классе.

Ответ. 5

9. Когда четырехзначное число удвоили и к результату прибавили 5, то получилось число, обратное данному. Что это за число?

Ответ. 1993

Занятие 14-15. Разные задачи

Урок-практикум – своеобразная самостоятельная работа; вариант, объем заданий учащиеся выбирают сами, исходя из уровня усвоения материала, мотивации развития, норм оценок. Каждому ученику предоставляется право проверить правильность решения каждого задания, получить консультацию учителя. Учитель выступает как субъект педагогической деятельности, помощник, а не контролер.

1. Из пункта А в пункт В едет трактор. Радиус переднего колеса трактора меньше радиуса заднего колеса. На пути из Л в В переднее колесо сделало на 200 оборотов больше, чем заднее. Если бы длина окружности переднего колеса была бы в 5/4 раза больше, то на пути из Л в В оно сделало бы на 80 оборотов больше, чем заднее колесо. Найти длины окружностей переднего и заднего колес трактора, если длина окружности заднего колеса на 1 м больше длины окружности переднего колеса.

Ответ.2:3м.

2. Известно, что 0,5 кг лука, 3 кг картофеля и 1 кг огурцов стоят вместе 2 руб. 38 коп., а 2 кг лука и 4 кг огурцов стоят 8 руб. 20 коп. Сколько стоят 1 кг лука, 2 кг картофеля и 2 кг огурцов вместе?
Ответ. 4 руб. 32 коп.

3. Кооперативу садоводов предлагается указать длину и ширину земельного участка прямоугольной формы, одна из сторон которого должна прилегать к шоссе. Нужно, чтобы площадь участка равнялась 150 га. Участок придется огородить забором, причем 1 м забора, прилегающего к шоссе, стоит 10руб., а 1 м забора на трех оставшихся сторонах — 5 руб. Какими должны быть стороны участка, чтобы стоимость забора была минимальной?
Ответ. 1000 м вдоль шоссе; 1500 м — перпендикулярно ему.

4. Поезд метро состоит из нескольких вагонов, причем в каждом вагоне находится одинаковое число пассажиров. Количество пассажиров в одном вагоне превосходит число вагонов на 9. Когда на станции во 2-й вагон вошло 10 человек, а из остальных вагонов вышло по 10 человек, то число пассажиров во втором вагоне оказалось равным числу пассажиров, оставшихся во всех остальных вагонах. Сколько пассажиров было первоначально в каждом вагоне?
Ответ.15.

5. Мелиораторы провели работы по осушению заболоченного прямоугольного участка площадью 2,7 га. Нужно было по двум наиболее коротким сторонам прокопать траншеи, а по двум другим — каналы. Сечение канала составляет 4 м2, траншеи — 2 ма. Определить длины сторон участка, если за время работ было вынуто 2760м3 грунта.
Ответ. 300 и 90 м.

6. В академическом собрании сочинений, включающем менее 20 томов, число томов с художественными произведениями кратно числу томов с письмами, которых в свою очередь в три раза меньше, чем томов с публицистикой. Если число томов с художественными произведениями увеличить в два раза, то их станет на 14 больше, чем томов с письмами. Сколько томов с публицистикой содержит собрание сочинений?
Ответ.6.

7. В магазин привезли 100 кг клюквы, состоящей на 99% из воды. После длительного хранения и усушки содержание воды в клюкве уменьшилось до 98%. Каким стал новый вес клюквы?

Ответ.50кг

8. Если идти шагом вверх по поднимающемуся эскалатору, то можно подняться на 10 с раньше, чем стоя на нем. Если же не идти, а бежать вверх, то можно выиграть еще 5 с. Пассажир, стоя на эскалаторе, поднялся на половину высоты эскалатора, после чего последний остановился. Вторую половину подъема пассажир прошел шагом. Сколько времени занял у него весь подъем, если известно, что человек бегает в два раза быстрее, чем ходит?
Ответ.45с.

9. Общий вес снаряжения туристской группы равен 202 кг. Если распределить его так, чтобы каждому юноше пришлось нести по 16 кг, а каждой девушке — по 9 кг, то 4 кг останутся нераспределенными. Поэтому юноши берут себе еще по 2 кг, в результате чего удается облегчить рюкзак каждой девушки на 1 кг, а одну из них освободить вовсе. При этом все снаряжение оказывается распределенным. Сколько юношей и девушек в туристской группе?

Ответ.9;6.

10. Два стрелка сделали по 30 выстрелов каждый; при этом было 44 попадания, остальные — промахи. Сколько раз попал каждый, если известно, что у пер- вого стрелка на каждый промах приходилось в два раза больше попаданий, чем у второго?

Ответ.24;20.

11. Смешав по 2 см3 трех веществ, получили 16 г смеси. Известно, что 4 г второго вещества занимает объем на 0,5 см3 больший, чем 4 г третьего вещества. Найти плотность третьего вещества, если известно, что масса второго вещества в смеси вдвое больше массы первого вещества.

Ответ.4г/см3.

12. Смесь равных объемов двух веществ имеет массу 62/13 г. Масса второго вещества в смеси равна массе 52/7 см3 первого вещества, а плотность второго вещества равна 1 г/см3. Найти объем каждого вещества в смеси.

Ответ.4см3.

13. Группу людей попытались построить в колонну по 8 человек в ряд, но один ряд оказался неполным. Тогда ту же группу людей перестроили по 7 человек в ряд: все ряды оказались полными, а число рядов оказалось на 2 больше. Если бы тех же людей попытались построить по 5 человек в ряд, то рядов было бы еще на 7 больше, причем один ряд был бы неполным. Сколько людей было в группе?

Ответ.119человек.

14. Имеется некоторое количество проволоки. Если ее намотать на катушки, на которые умещается по 800 м проволоки, то одна катушка будет намотана не полностью. То же самое произойдет, если пользоваться только катушками, на которые умещается по 900 м проволоки, причем таких катушек понадобится на 3 меньше. Если же проволоку наматывать только на катушки, на которые умещается по 1100 м, то таких катушек понадобится еще на 6 меньше, но при этом все такие катушки будут намотаны полностью. Сколько метров проволоки было?

Ответ.52900м.

Занятие 16. Итоговая зачетная работа.

Решение учеником в качестве индивидуального задания предложенных учителем задач из того списка, что завершает каждый модуль.

Учащимся, ориентированным на выполнение заданий более высокого уровня сложности, предлагается:

Самостоятельное изучение некоторых вопросов курса с последующей презентацией (программные продукты Microsoft Power Point).

Самостоятельное решение предложенных задач с последующим разбором вариантов решений.

Самостоятельное построение метода, позволяющего решить предложенную задачу.

Самостоятельный подбор задач на изучаемую тему курса из дополнительной математической литературы.

Итоговое занятие предлагается провести в форме круглого стола с презентациями каждого модуля курса.

Список литературы.

1. Кузнецова Л.В.«Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. - М.: ДРОФА, 2010.

2. Журналы «Математика в школе» №4/2010 №9/2013, №8/2013, №5/2013, №8/2012, №5/2012.