Разработка дидактических материалов по теме "Решение задач с параметрами"
Муниципальное образование город Краснодар
муниципальное бюджетное общеобразовательное учреждение
муниципального образования город Краснодар
средняя общеобразовательная школа № 47 г. Краснодар
РАЗРАБОТКА ДИДАКТИЧЕСКИХ МАТЕРИАЛОВ ПО ТЕМЕ
«РЕШЕНИЕ ЗАДАЧ С ПАРАМЕТРАМИ»
подготовила
учитель математики
Чепрасова Анна Валериевна
г. Краснодар
2014
Под задачами с параметрами понимаются задачи, в которых ход решения и форма результата зависят от входящих в условие величин, численные значения которых не заданы конкретно, но считаются известными; эти величины называются параметрами. Задачи такого типа для школьников являются наиболее сложными. Поэтому прежде, чем приступать к решению задач с параметрами, важно, чтобы учащиеся видели, что является параметром в том или ином случае. Для этого целесообразно сначала решить следующие задания:
1) Дано уравнение
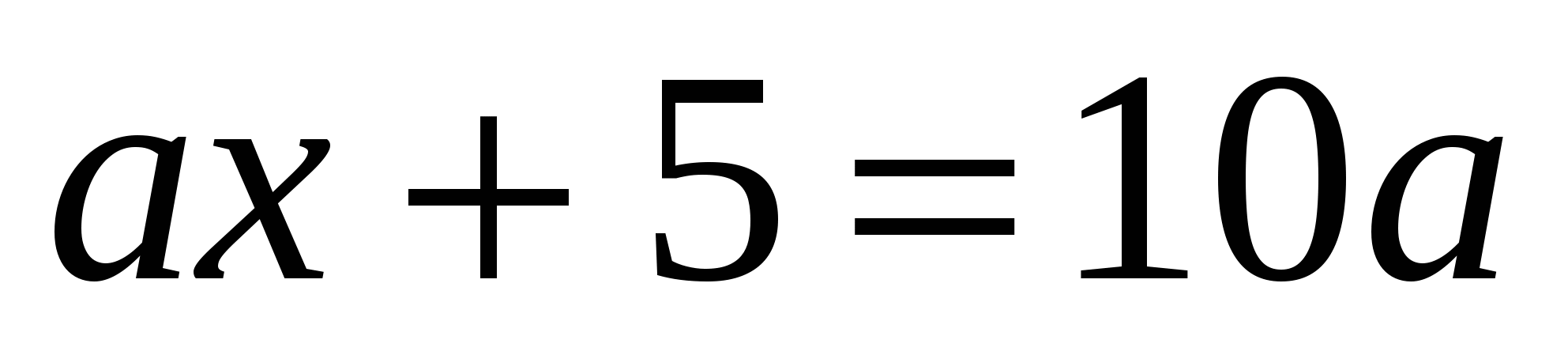 с параметром a. Напишите уравнение, которое получится при:
с параметром a. Напишите уравнение, которое получится при:
а) a = 2; б) a = – 4; в) a = 0; г) a = ![]() ; д) a =
; д) a = ![]() .
.
2) Дано уравнение ![]() с параметром x. Напишите уравнение, которое получится при:
с параметром x. Напишите уравнение, которое получится при:
а) x = 3; б) x = - 1,5; в) x = ![]() ; г) x = 0; д) x = - 20.
; г) x = 0; д) x = - 20.
1) Является ли линейным относительно x уравнение
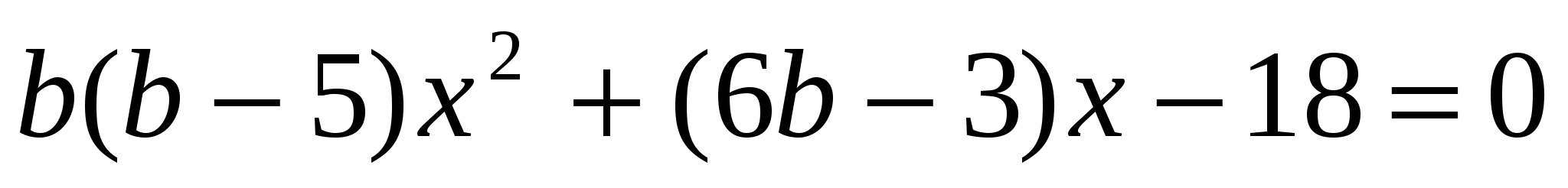 при:
при:
а) b = 6; б) b = 0; в) b = 0,5; г) b = 5?
2) В каких из указанных случаев уравнение ![]() не является линейным относительно y:
не является линейным относительно y:
а) при m = 6; б) при m = 0; в) при m = 5; г) при m = - 0,5.
Какие случаи следует выделить при решении уравнения с параметром c:
а) ![]() ; б)
; б) ![]() ?
?
Решите уравнение относительно x:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
При каких значениях параметра d уравнение
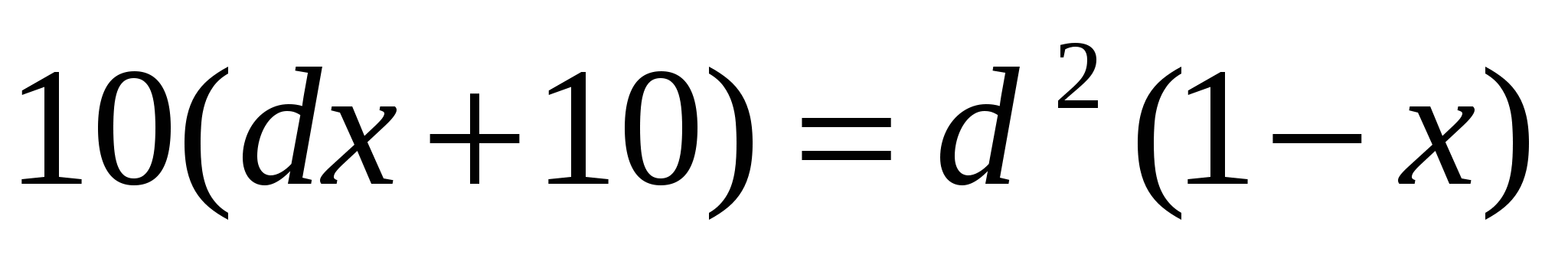 :
:
а) имеет единственный корень; б) не имеет корней;
в) имеет бесконечное множество корней?
С понятием параметра, по существу, встречаются уже в седьмом классе при изучении линейных уравнений и линейной функции. А значит, и знакомить учащихся с параметрами полезно при изучении линейных уравнений. Это надо делать для того, чтобы ученики привыкли к понятию «параметр» и в старших классах при более детальном изучении задач с параметрами испытывали меньше затруднений. Кроме того, задачи с параметрами хорошо развивают логическое мышление, тренируют память и внимание.
При изучении линейных уравнений можно предложить следующие задания:
Решите уравнение относительно x:
ВАРИАНТ 1. ВАРИАНТ 2.
а) ax = 1; а) ![]() ;
;
б) 3cx = 4; б) ![]() ;
;
в) b + 5x = - 7; в) ![]() ;
;
г) - 0,6m – 0,2x = 0; г) ![]() ;
;
д) ![]() ; д)
; д) ![]() ;
;
е) 2(b + 3)x = 9; е) ![]() ;
;
ж) ![]() ; ж)
; ж) ![]() ;
;
з) ![]() ; з)
; з) ![]() ;
;
и) ![]() ; и)
; и) ![]() ;
;
к) ![]() ; к)
; к) ![]() ;
;
л) ![]() ; л)
; л) ![]() ;
;
м) ![]() ; м)
; м) ![]() ;
;
н) ![]() ; н)
; н) ![]() ;
;
о) ![]() ; о)
; о) ![]() .
.
При каких значениях параметра b уравнение не имеет корней:
ВАРИАНТ 1. ВАРИАНТ 2.
а) ![]() ; а)
; а) ![]() ;
;
б) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; в)
; в) ![]() ;
;
г) ![]() . г)
. г) ![]() .
.
Указать, при каких значениях параметра уравнения имеют бесконечно много корней:
ВАРИАНТ 1. ВАРИАНТ 2.
а) ![]() ; а)
; а) ![]() ;
;
б) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; в)
; в) ![]() ;
;
г) ![]() . г)
. г) ![]() .
.
1) При каком значении параметра a уравнение
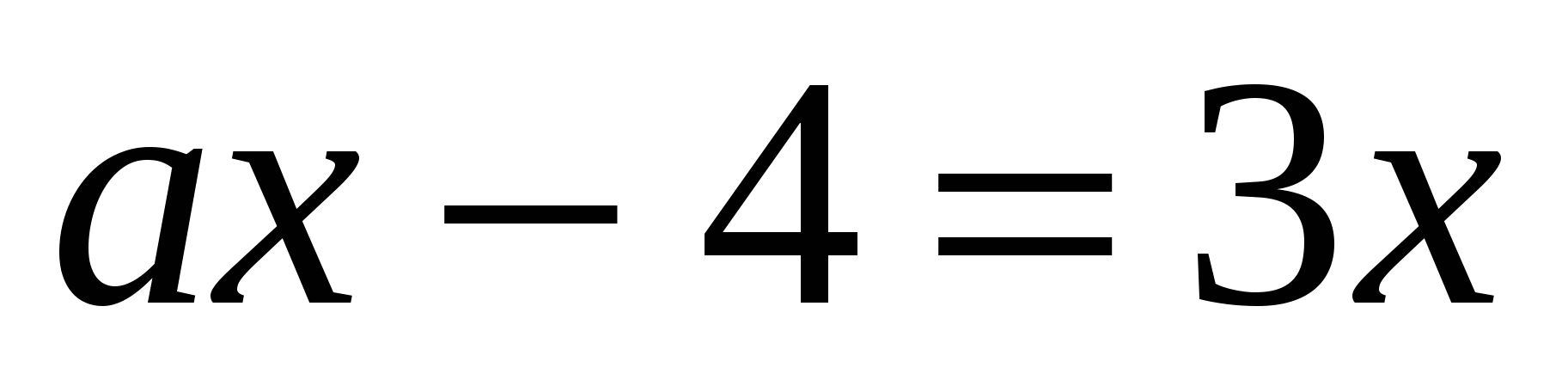 имеет корень, равный 8?
имеет корень, равный 8?
2) При каком значении параметра b уравнение ![]() имеет корень, рав-
имеет корень, рав-
ный 12?
1) При каком значении параметра с уравнения
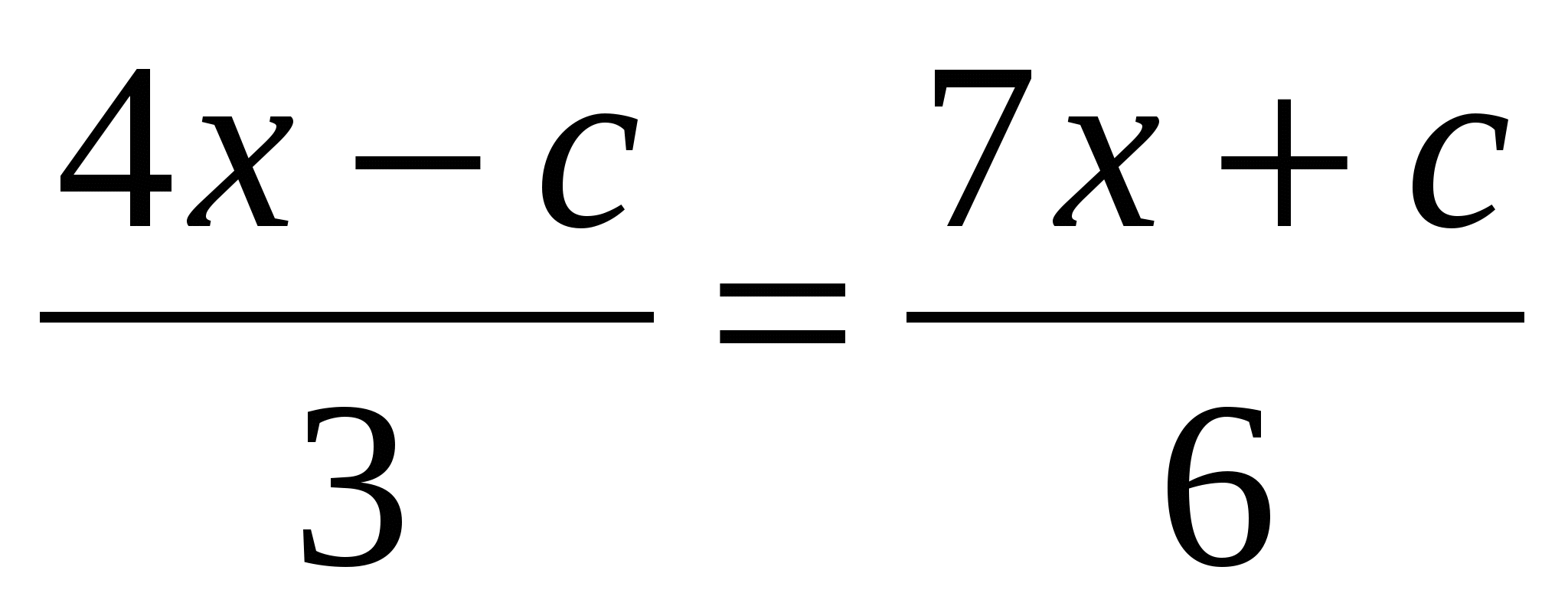 и
и 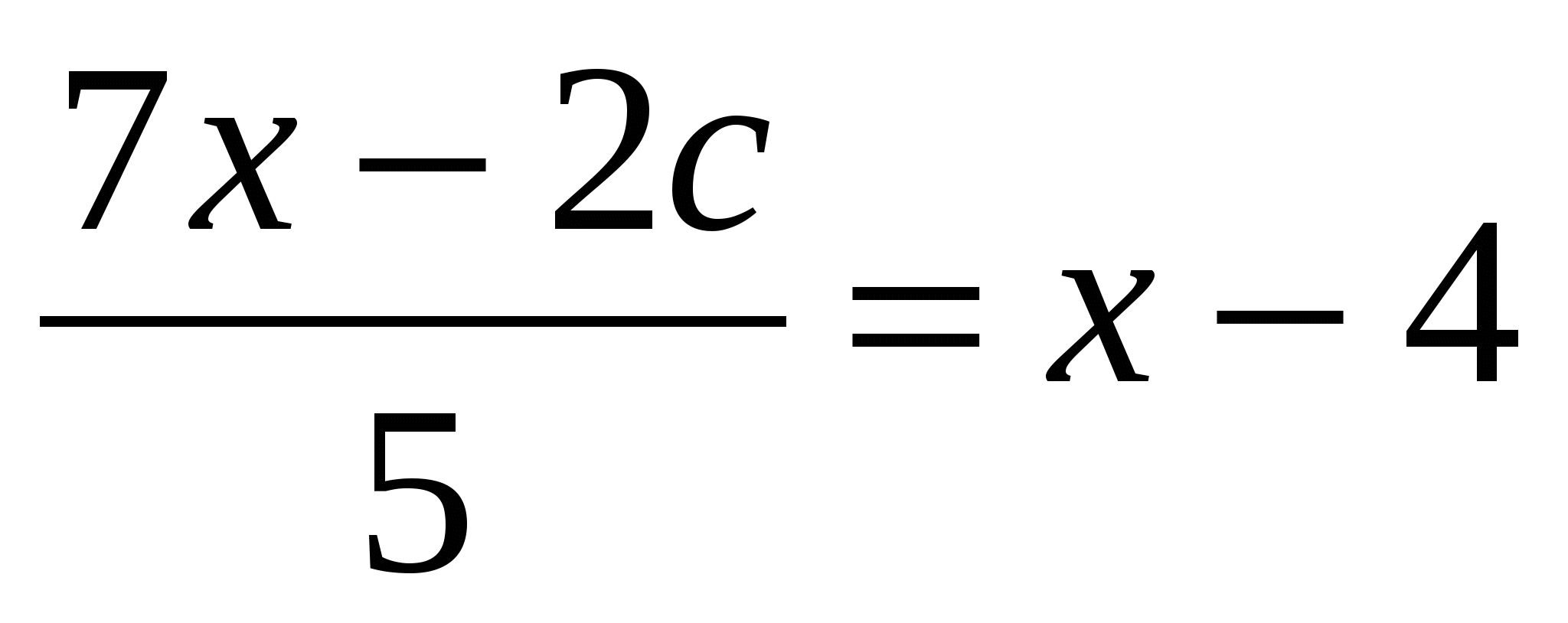 имеют равные корни?
имеют равные корни?
2) При каком значении параметра b уравнения ![]() и
и ![]() имеют равные корни?
имеют равные корни?
При изучении темы «Линейная функция и ее график» также можно рассмотреть задания, содержащие параметры.
1) При каком значении параметра c прямая
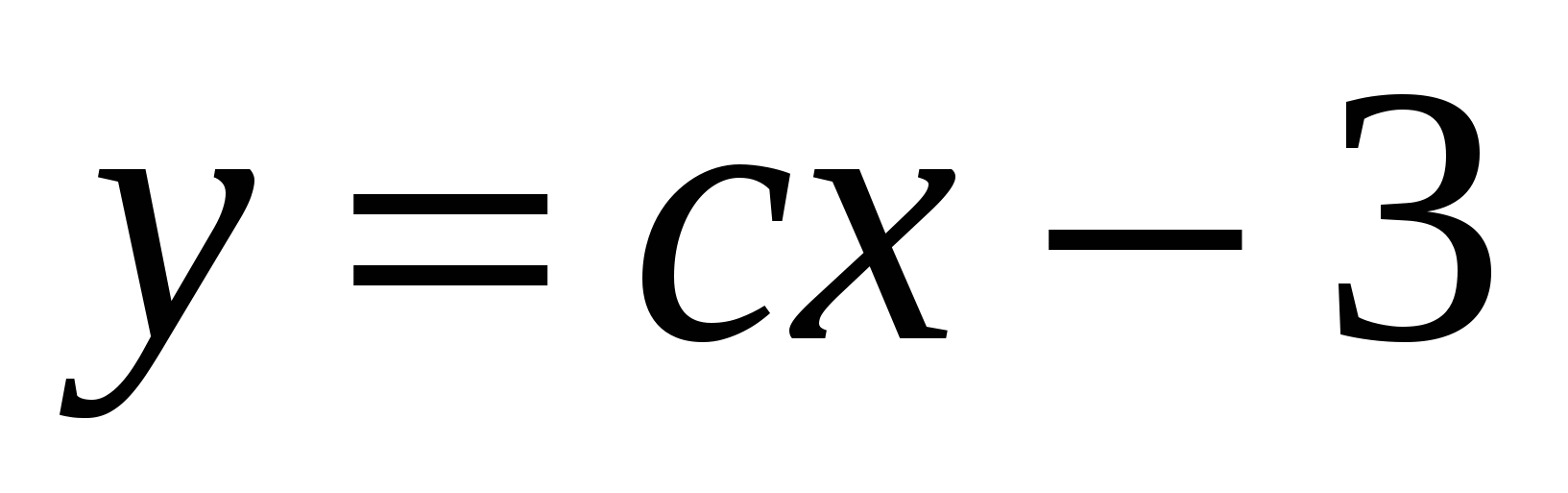 проходит через точку A(-2; 9)?
проходит через точку A(-2; 9)?
2) При каком значении параметра d прямая ![]() проходит через точку B(5; - 6)?
проходит через точку B(5; - 6)?
1) При каком значении параметра n прямая
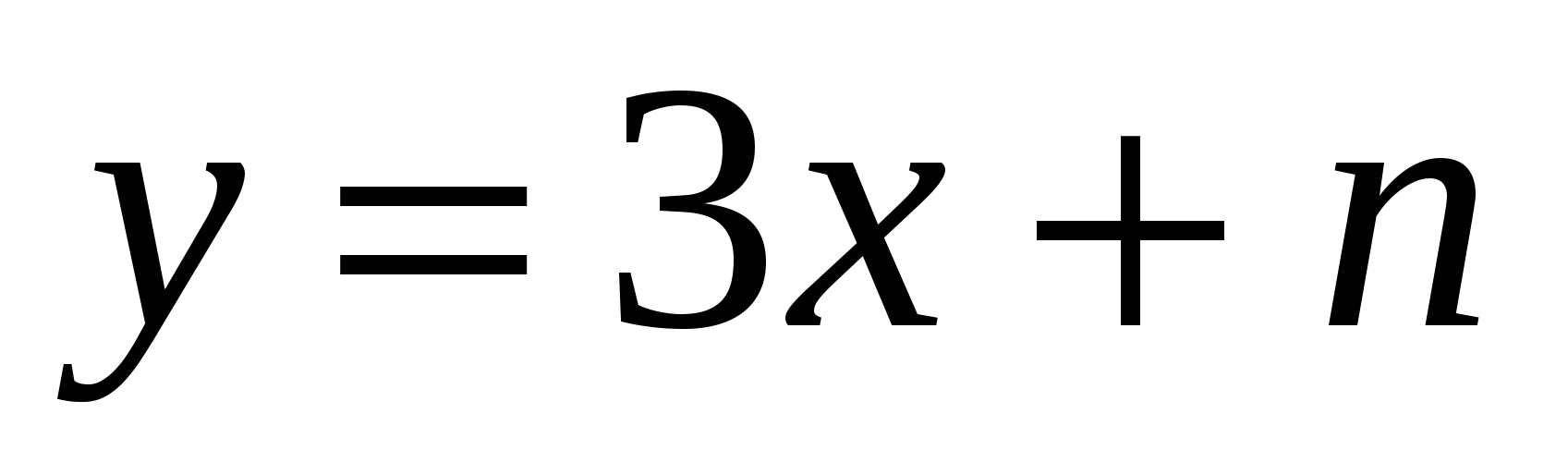 проходит через точку C(-1; 5)?
проходит через точку C(-1; 5)?
2) При каком значении параметра b прямая ![]() проходит через точку M(-4; 1)?
проходит через точку M(-4; 1)?
1) При каком значении параметра a прямые
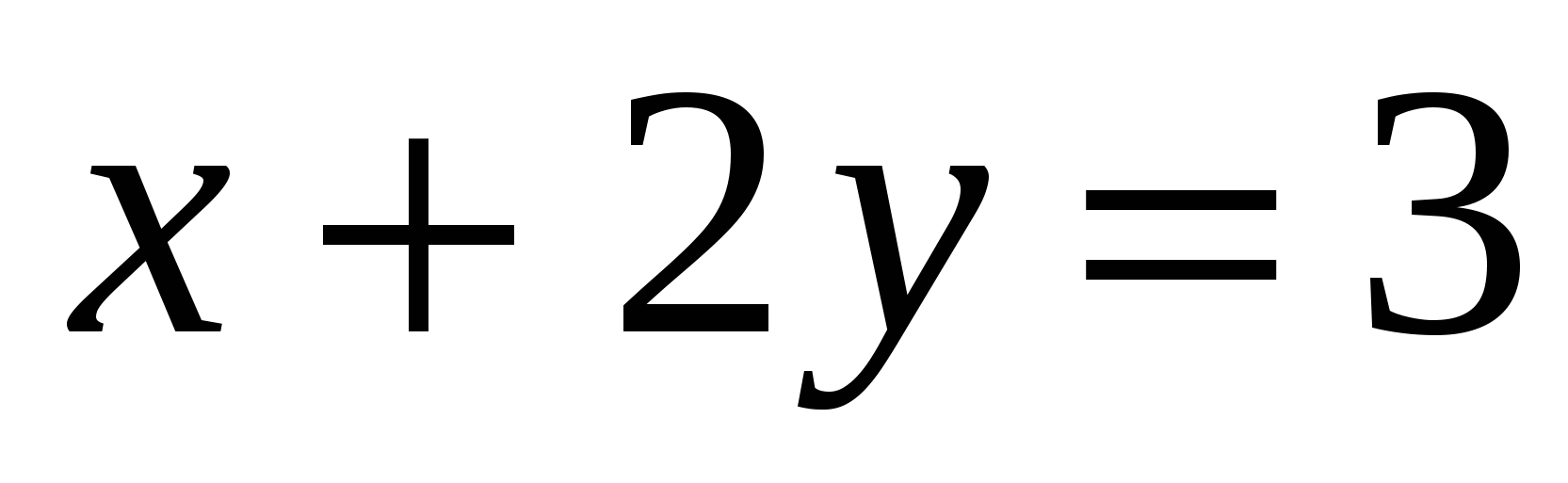 и
и 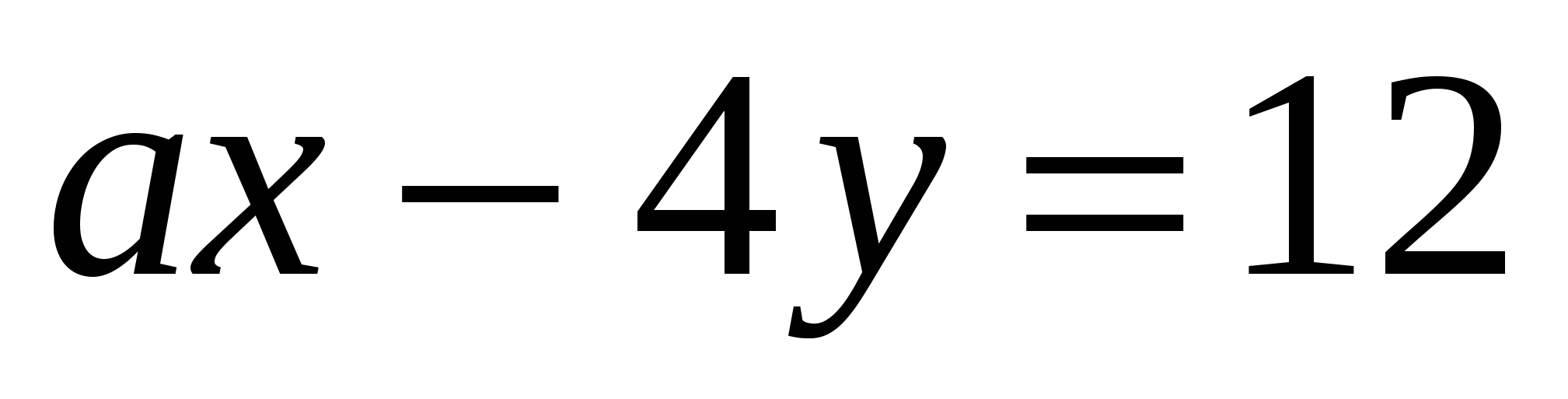 пересекаются в точке, принадлежащей оси абсцисс?
пересекаются в точке, принадлежащей оси абсцисс?
2) При каком значении параметра b прямые ![]() и
и ![]() пересекаются в точке, принадлежащей оси ординат?
пересекаются в точке, принадлежащей оси ординат?
1) Графики функций
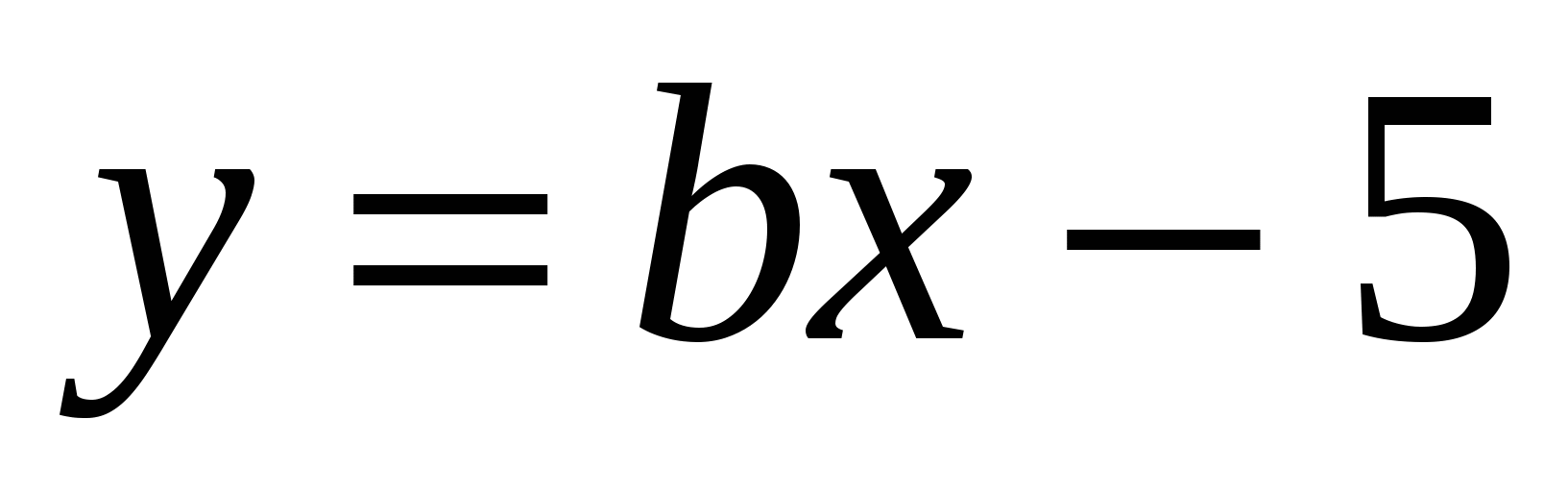 и
и 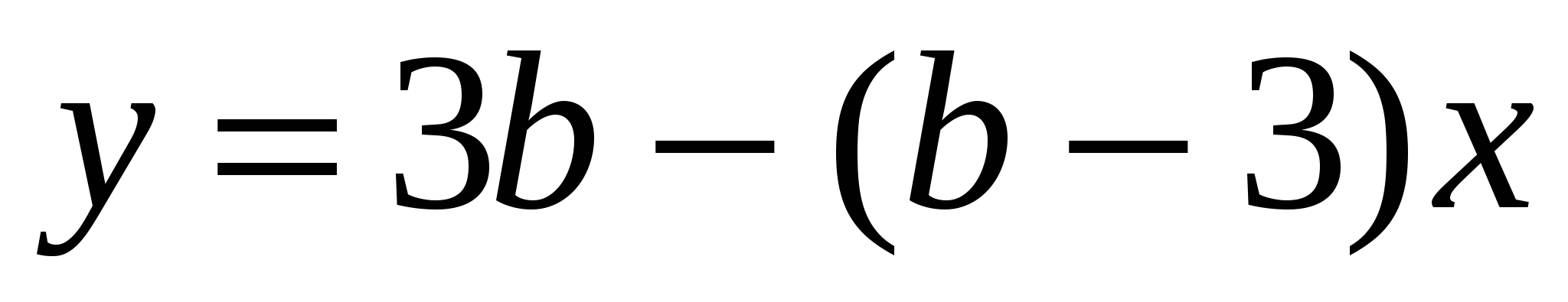 пересекаются в точке с абсциссой, равной –8 . Найдите ординату точки пересечения.
пересекаются в точке с абсциссой, равной –8 . Найдите ординату точки пересечения.
2) Графики функций ![]() и
и ![]() пересекаются в точке с абсциссой, равной –2. Найдите ординату точки пересечения.
пересекаются в точке с абсциссой, равной –2. Найдите ординату точки пересечения.
1) Графики функций
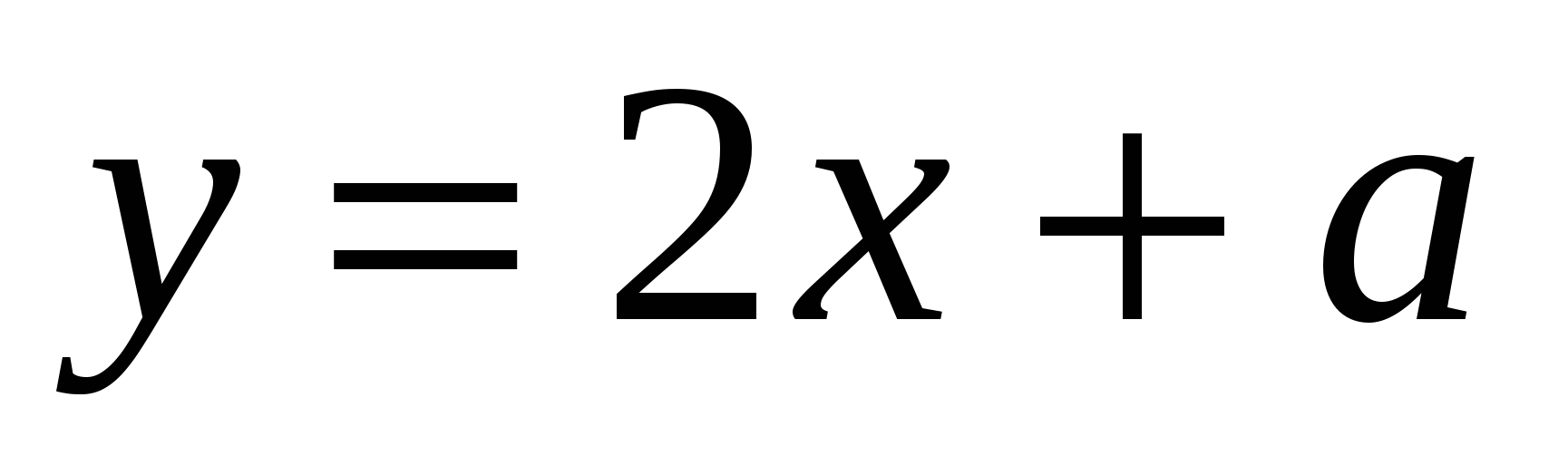 и
и 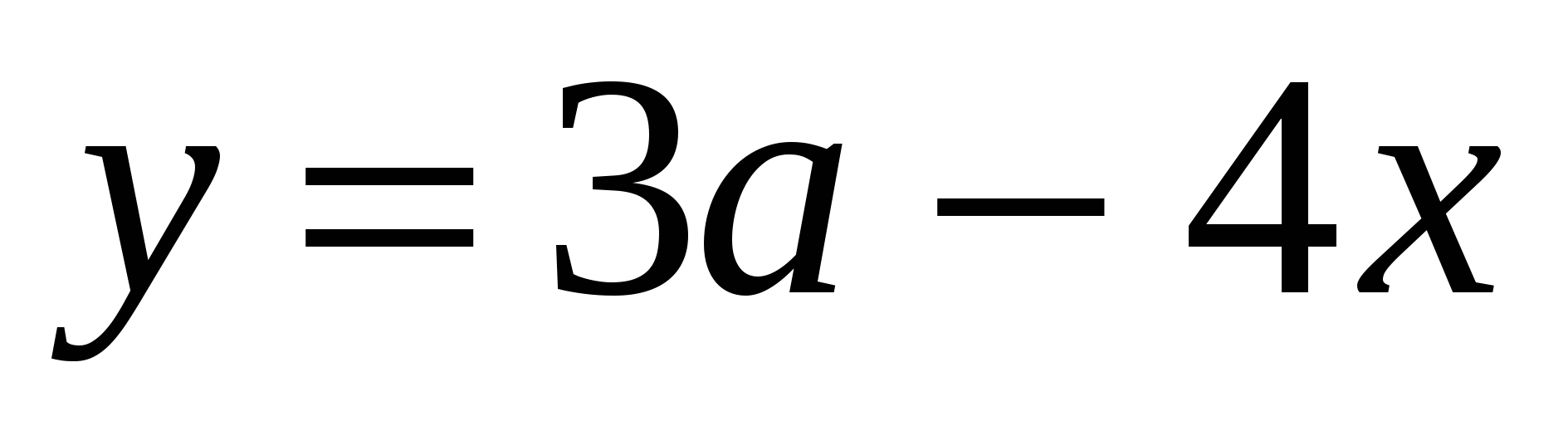 пересекаются в точке с ординатой, равной 4. Найдите абсциссу точки пересечения.
пересекаются в точке с ординатой, равной 4. Найдите абсциссу точки пересечения.
2) Графики функций ![]()
![]() пересекаются в точке с ординатой,
пересекаются в точке с ординатой,
равной 13. Найдите абсциссу точки пересечения.
1) Графики функций
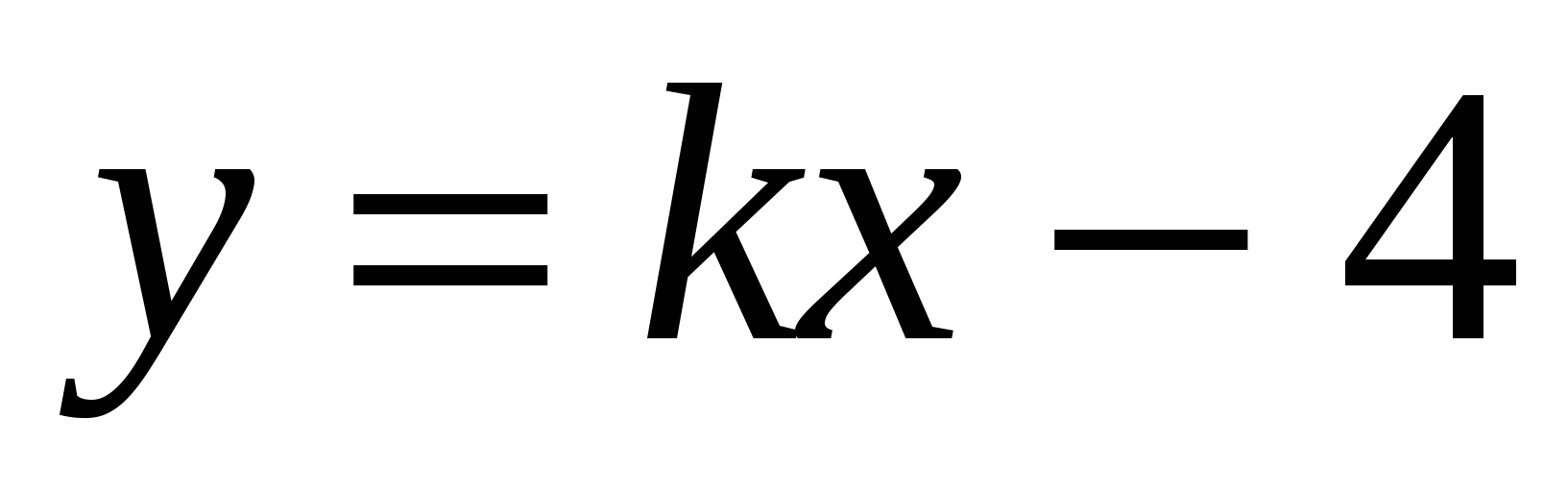 и
и 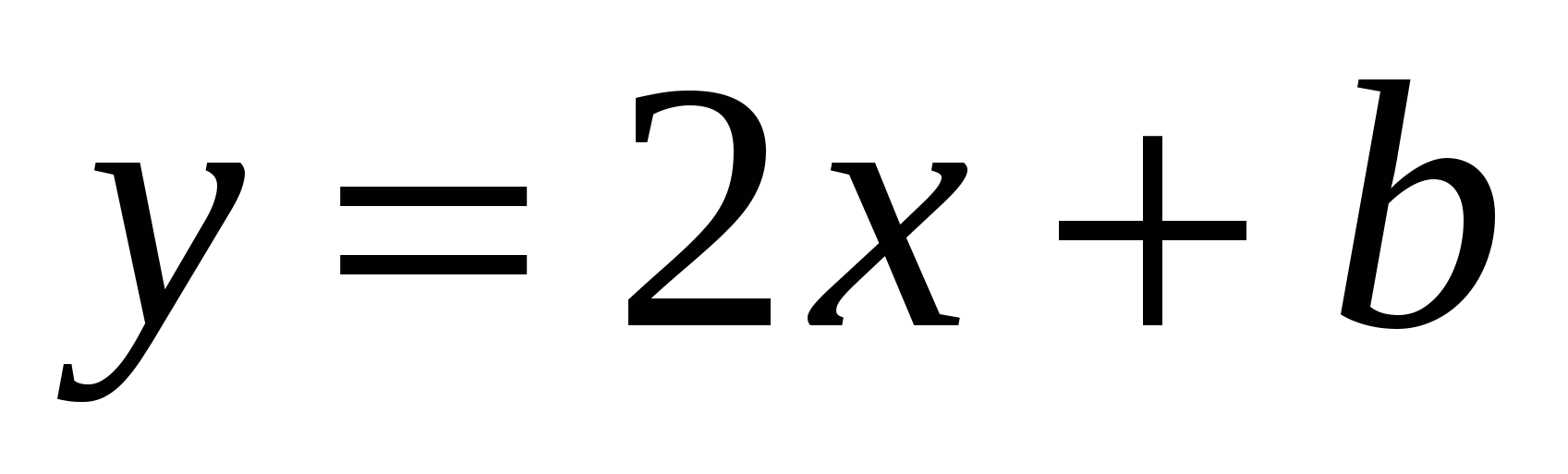 симметричны относительно оси абсцисс.
симметричны относительно оси абсцисс.
а) Найдите b и k.
б) Найдите точку пересечения этих графиков.
2) Графики функций ![]() и
и ![]() симметричны относительно оси
симметричны относительно оси
ординат.
а) Найдите b и k.
б) Найдите точку пересечения этих графиков.
Задания, содержащие параметры, можно предложить и при решении систем линейных уравнений.
1) При каких значениях параметра a система
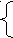
![]() ,
,
![]() :
:
а) имеет бесконечное множество решений;
б) имеет единственное решение?
2) При каких значениях параметра система
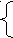
![]() ,
,
![]() :
:
а) имеет бесконечное множество решений;
б) имеет единственное решение.
П
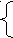
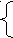 ри каких значениях параметра a системы не имеют решений?
ри каких значениях параметра a системы не имеют решений?
а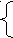 )
) ![]() , б)
, б) ![]() , в)
, в) ![]() ,
,
![]() ;
; ![]() ;
; ![]() ;
;
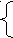
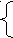 г)
г) ![]() , д)
, д) ![]() ,
,
![]() ;
; ![]() .
.
При каких значениях параметра a системы имеют бесконечно много решений?
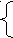
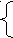
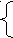 а)
а) ![]() , б)
, б) ![]() , в)
, в) ![]() ,
,
![]() ;
; ![]() ;
; ![]() ;
;
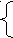
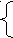 г)
г) ![]() , д)
, д) ![]() ,
,
![]() ;
; ![]() .
.
Р
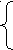
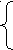
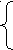
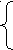 ешите систему уравнений относительно x и y:
ешите систему уравнений относительно x и y:
а) ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]() ,
,
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
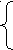
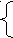
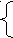
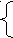 д)
д) ![]() , е)
, е) ![]() , ж)
, ж) ![]() , з)
, з) ![]() ,
,
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
 и)
и) ![]() , к)
, к) ![]() , л)
, л) ![]() ,
,
![]() ;
; ![]() ;
; ![]() .
.
Продолжить рассмотрение задач с параметрами следует при изучении квадратного трехчлена ![]() , т. е. при решении квадратных и дробно-рациональных уравнений и текстовых задач, в ходе решения которых составляются такие уравнения. При этом очень важно хорошо знать не только формулы корней квадратного трехчлена, но и теорему Виета: корни
, т. е. при решении квадратных и дробно-рациональных уравнений и текстовых задач, в ходе решения которых составляются такие уравнения. При этом очень важно хорошо знать не только формулы корней квадратного трехчлена, но и теорему Виета: корни ![]() и
и ![]() квадратного трехчлена
квадратного трехчлена ![]() удовлетворяют соотношениям:
удовлетворяют соотношениям:
![]() ,
,
![]() .
.
Если ![]() – единственный корень, то в теореме Виета следует положить
– единственный корень, то в теореме Виета следует положить ![]() . Тогда
. Тогда ![]() ,
, ![]() . Верно и обратное утверждение: если числа
. Верно и обратное утверждение: если числа ![]() таковы, что выполнены написанные выше соотношения, то
таковы, что выполнены написанные выше соотношения, то ![]() и
и ![]() являются корнями квадратного трехчлена
являются корнями квадратного трехчлена ![]() . Очень важны при решении задач следствия из теоремы Виета.
. Очень важны при решении задач следствия из теоремы Виета.
СЛЕДСТВИЕ 1. Для того, чтобы квадратный трехчлен имел корни одного знака, необходимо и достаточно, чтобы были выполнены условия D > 0, ![]() > 0.
> 0.
При этом оба корня положительны, если дополнительно выполнено условие ![]() < 0, и отрицательны, если
< 0, и отрицательны, если ![]() < 0.
< 0.
СЛЕДСТВИЕ 2. Для того чтобы квадратный трехчлен имел два корня разных знаков, необходимо и достаточно выполнение условий D > 0, ![]() < 0.
< 0.
При каких значениях c уравнения
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д)![]() ; е)
; е) ![]() ;
;
ж)![]()
не имеют корней? (Для ответа на вопрос задачи достаточно решить неравенство D < 0 относительно c).
При каких значениях параметра d уравнения имеют один корень?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е)![]() ; ж)
; ж)![]() .
.
(Для ответа на вопрос задачи достаточно решить уравнение D = 0 относительно d).
При каких значениях параметра a уравнения имеют два различных корня?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е)![]() .
.
(Для ответа на вопрос задачи достаточно решить неравенство D >0 относительно a).
При каких значениях параметра k оба корня квадратного уравнения
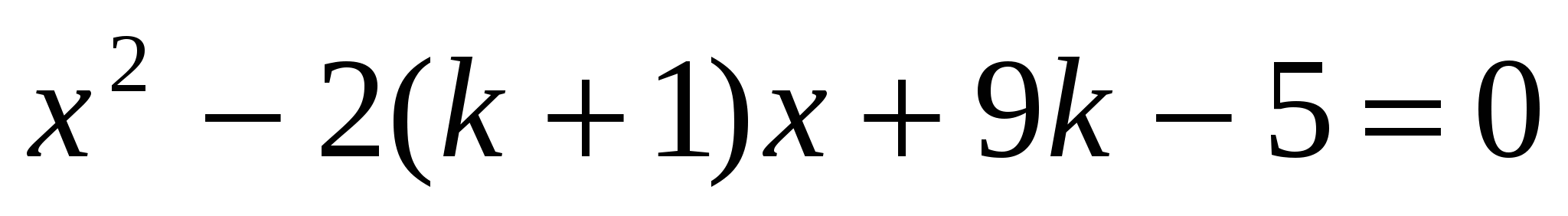 положительны?
положительны?Определите значение параметра n, при котором оба корня уравнения
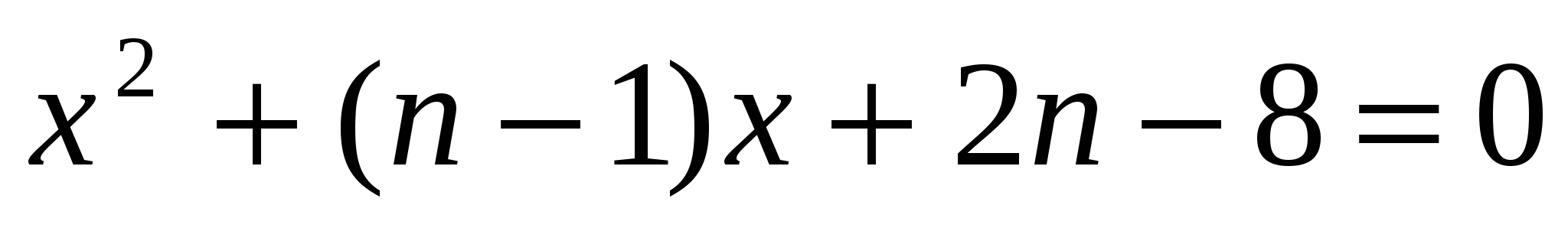 отрицательны?
отрицательны?Решите относительно x уравнения:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() .
.
Решите относительно y уравнения:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д)![]() .
.
При решении задач с параметрами возникают различные уравнения, но в этих случаях приходится учитывать допустимые значения параметра, определяемые смыслом задачи. Иногда границы, в которых заключены значения параметра, приходится устанавливать, проводя дополнительные исследования. Следующие задачи решить в целых числах.
За два дня вспахано 80 га, причем в первый день вспахано на a га больше, чем во второй день. Сколько гектаров земли вспахано во второй день?
Проволоку длиной 135 м разрезали на две части так, что одна из них короче другой в n раз. Найти длину каждой части, зная, что их длины выражаются целым числом метров. (45м и 90м; 27м и 108м; 15м и 120м; 9м и 126м; 5м и 130м; 3м и 132м; 1м и 134м).
Катер прошел расстояние между пристанями по течению реки за 2 ч, а обратно против течения – за 3 ч. Найти собственную скорость катера, если скорость течения реки m км/ч. (5m км/ч).
Купили n м ткани двух сортов по цене 2 р. за метр и 3 р. за метр. За всю покупку заплатили 22р. Сколько метров ткани каждого сорта купили, если
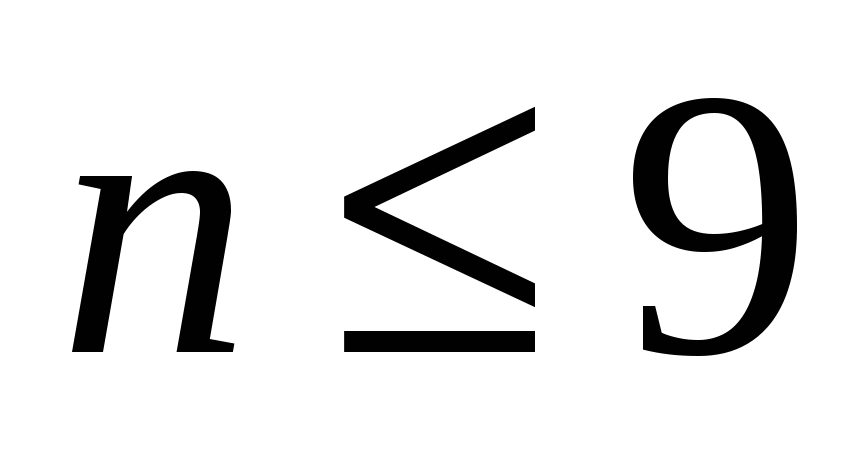 ?
?
(5 м и 4м).
Двое рабочих изготовили вместе 74 детали. Первый изготовлял в день на s деталей больше второго и работал 7 дней, а второй – 8 дней. Сколько деталей в день изготовлял каждый рабочий? (6 деталей и 4 детали).
В трех корзинах 54 кг яблок. В первой корзине на 12 кг яблок меньше, чем во второй, а в третьей – в n раз больше, чем в первой. Сколько килограммов яблок в каждой корзине? (1, 13, 40; 2, 14, 38; 3, 15, 36; 6, 18, 30; 7, 19, 28).
Гипотенуза прямоугольного треугольника равна 13 см. Один из катетов на k см больше другого. Найти катеты прямоугольного треугольника. (5см и 12см).
Турист прошел 3 км по шоссе и s км – по проселочной дороге, затратив на весь путь 2ч. По шоссе он шел со скоростью на 2 км/ч большей, чем по проселку. С какой скоростью шел турист по проселку? (1 км/ч; 4 км/ч).
О Т В Е Т Ы.
Понятие параметра. 1. 1) а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() .
.
2) а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
2.1) а) нет; б) да; в)нет; г) да.
в случаях а) и б).
3. а) c = 0; c 0; б) c = 0; c = 4; c 0 и c 4.
4. а) ![]() , a 0; корней нет, a = 0; б) x = 1, a 0; бесконечно много
, a 0; корней нет, a = 0; б) x = 1, a 0; бесконечно много
корней, a = 0; в) x = 3, a 0; бесконечно много корней, a = 0.
а) при d 0 и d - 10; б) при d = 0; в) d = - 10.
Решение линейных ВАРИАНТ 1.
уравнений. 1. а) ![]() a 0; ж)
a 0; ж) ![]() ;
;
корней нет, a = 0; з) ![]() , a 0;
, a 0;
б) ![]() , c 0; корней нет, a = 0;
, c 0; корней нет, a = 0;
корней нет, c = 0; и) ![]() , a -1;
, a -1;
в) ![]() ; корней нет, a = - 1;
; корней нет, a = - 1;
г) ![]() ; к)
; к) ![]() , d 8;
, d 8;
д) ![]() , a 0; корней нет, d = 8;
, a 0; корней нет, d = 8;
корней нет, a = 0; л) ![]() , a 0;
, a 0;
е) ![]() , b - 3; корней нет, a = 0, b 0;
, b - 3; корней нет, a = 0, b 0;
корней нет, b = - 3; бесконечно много корней, a = 0; b = 0;
м) ![]() , b 0;
, b 0;
корней нет, b = 0, a 1;
бесконечно много корней, b = 0, a = 1;
н) ![]() , b 0;
, b 0;
корней нет, b = 0, a 3;
бесконечно много корней, b = 0, a = 3;
о) ![]() .
.
2. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г) нет.
; г) нет.
4. 1) при a = 3,5; 2) при b = 4,5.
5.1) при с = -2,5; 2) при b = ![]() .
.
Линейная функция 1. 1) –6; 2) –2. 2. 1) 8; 2) 29. 3. 1) 4; 2) – 4.
и ее график. 4. 1) - 13; 2) – 2. 5. 1) 0,8; 2) 1. 6. 1) b = 4, k = 2. 2) b = -6, k = - 4.
Решение систем 1. 1) а) 4; б) при a 4. 2) а) – 2; б) при b - 2. 2. а) 0; б) – 12;
линейных уравнений. в) –3 и 2; г) –2 и – 4; д) –1 и 1. 3. а) 1; б) 3; в) 3; г) –3; д) 0.
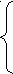 4. а)
4. а) ![]() , б) a
, б) a ![]()
![]() , при a
, при a ![]()
![]() ;
; ![]() ; корней нет;
; корней нет;
в) ![]()
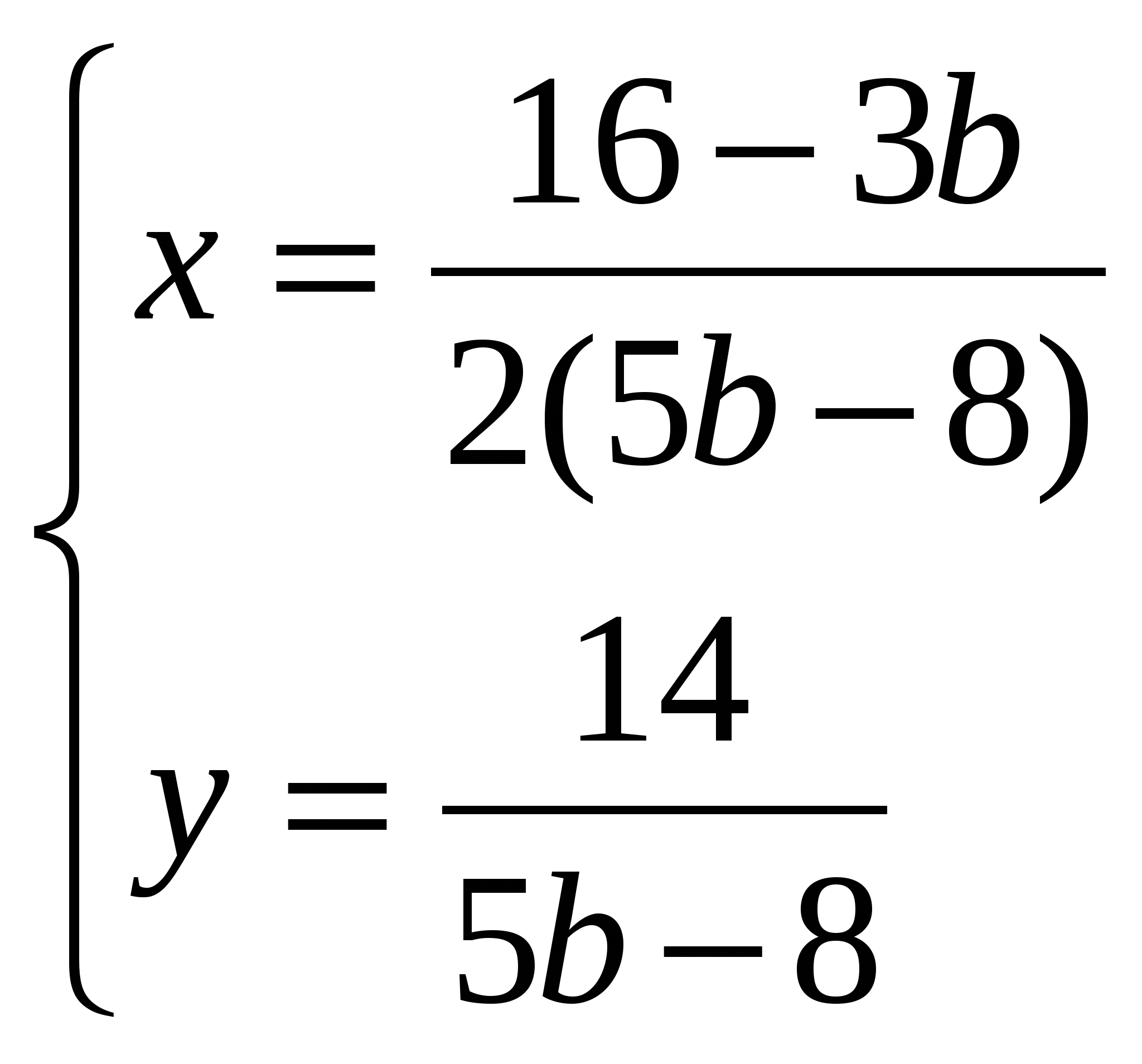 ; при b = 1,6 корней нет.
; при b = 1,6 корней нет.
Список использованной литературы.
Сборник развивающих задач с решениями по математике для 5-6 классов. / В.К. Совайленко, О.В. Лебедева. – Ростов-на-Дону:Легион, 2005. 256с.
Текстовые задачи: Пособие для учащихся. / А.В. Шевкин. – М.: Просвещение, 1997. – 112с.
Уроки математики с применением информационных технологий. 5-10 классы. Методическое пособие с электронным приложением / Л.И. Горохова и др. – М.: Издательство «Глобус», 2009. – 266 с.
Алгебра. Тесты для промежуточной аттестации. 7-8 класс. Издание третье, переработанное и дополненное. Под редакцией Ф. Ф. Лысенко. Ростов-на-Дону: Легион, 2008. – 224 с.
Чулков П. В. и др. Алгебра. Тесты. 7-9 класс – М.: «Издат-Школа», 1998. – 192 с.
Алгебра. 7 – 9 классы. Тесты для учащихся общеобразовательных учреждений / А. Г. Мордкович, Е. Е. Тульчинская ; под ред. А. Г. Мордковича. – 8-е изд., стер. – М. : Мнемозина, 2009. – 119 с. : ил.
Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре и геометрии для 9 класса.-М.:Илекса, - 2005, - 192 с.
Математика. 9 класс. Тематические тесты для подготовки к ГИА- 2012. Алгебра, геометрия, теория вероятностей и статистика: учебно-методическое пособие/Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова. – Ростов н/Д: Легион-М, 2011. – 314 с. – (ГИА-9)
Математика. Приложение к газете «Первое сентября».

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ