Реализация требований ФГОС ООО при обучении учащихся 9 класса теме: “Элементы комбинаторики”

Реализация требований ФГОС ООО

при обучении учащихся 9 класса теме:

“Элементы комбинаторики”

Учитель математики МАОУ г.о. Балашиха «Земская гимназия»

Синюкова Елена Николаевна

2013

ВВЕДЕНИЕ

Актуальность

Цель работы: Реализация требований ФГОС ООО при изучении темы: «Элементы комбинаторики»

Для достижения поставленной цели необходимо решение следующих задач.

Задачи исследования:

1. Выявить теоретические основы обучения теме, связанные с реализацией ФГОС ООО.

2. Выполнить отбор средств обучения теме, в том числе средства ИКТ

3. Разработать таблицу целей и карту обучения теме.

4. «Тематическое планирование образовательных результатов освоения математики по теме «Элементы комбинаторики»

5. Разработать методические рекомендации обучения теме и применить их в учебном процессе (фрагмента урока, иллюстрирующего развитие и формирование УУД при обучении данной теме школьного курса математики).

Решение поставленных задач потребовало использования следующих методов исследования: анализ психолого- педагогической, математической и методической литературы по проблеме исследования, учебников и учебных пособий по математике; беседы с учителями.

ГЛАВА 1. Теоретические основы обучения теме «Элементы комбинаторики»

§ 1 Концепция духовно-нравственного развития и воспитания личности гражданина России

Изучив необходимые документы и с учётом темы проекта: «Элементы комбинаторики. Множества. Элементы логики» по УМК Алгебра 9 класс, Ю.Н. Макарычев и др. Москва. «Просвещение», 2011 год, можно выделить следующие основные моменты.

Концепция духовно-нравственного развития и воспитания личности гражданина России является методологической основой разработки и реализации федерального государственного образовательного стандарта общего образования.

Современный национальный воспитательный идеал — это высоконравственный, творческий, компетентный гражданин России, принимающий судьбу Отечества как свою личную, осознающий ответственность за настоящее и будущее своей страны, укоренённый в духовных и культурных традициях многонационального народа Российской Федерации. Поэтому развитие и воспитание обучающихся должно происходить по трём основным направлениям:

в сфере личностного развития
в сфере общественных отношений
в сфере государственных отношений

Организация социально открытого пространства духовно-нравственного развития и воспитания личности гражданина России, нравственного уклада жизни обучающихся осуществляется на основе: нравственного примера педагога; социально-педагогического партнёрства; индивидуально-личностного развития; интегративности программ духовно-нравственного воспитания; социальной востребованности воспитания.

Федеральный государственный образовательный стандарт основного общего образования устанавливает требования к результатам освоения обучающимися основной образовательной программы основного общего образования: личностные, метапредметные, предметные. Концепция духовно-нравственного развития и воспитания личности гражданина России отражается в личностных результатах освоения основной образовательной программы основного общего образования.

В требованиях к структуре основной образовательной программы основного общего образования указано, что должна содержать три раздела: целевой, содержательный и организационный. В содержательном разделе подробно описаны требования к Программе развития универсальных учебных действий (программа формирования общеучебных умений и навыков) на ступени основного общего образования. УУД обеспечивают способность учащегося к саморазвитию и самосовершенствованию посредством сознательного и активного присвоения социального опыта.

В целях реализации ФГОС ООО раздел «Элементы комбинаторики и теории вероятностей» сравнительно недавно появился в УМК. Предметные результаты освоения основной образовательной программы основного общего образования с учётом общих требований Стандарта и специфики изучаемых предметов, входящих в состав предметных областей, должны обеспечивать успешное обучение на следующей ступени общего образования:

Математика. Алгебра. Геометрия. Информатика:

1) формирование представлений о математике как о методе познания действительности, позволяющем описывать и изучать реальные процессы и явления;

2) развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования, доказательства математических утверждений;

8) овладение простейшими способами представления и анализа статистических данных; формирование представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о простейших вероятностных моделях; развитие умений извлекать информацию, представленную в таблицах, на диаграммах, графиках, описывать и анализировать массивы числовых данных с помощью подходящих статистических характеристик, использовать понимание вероятностных свойств окружающих явлений при принятии решений;

9) развитие умений применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, компьютера, пользоваться оценкой и прикидкой при практических расчётах;

14) формирование навыков и умений безопасного и целесообразного поведения при работе с компьютерными программами и в Интернете, умения соблюдать нормы информационной этики и права.

§ 2 Логико- дидактический анализ темы «Элементы комбинаторики»

Логико-дидактический анализ содержания раздела «Элементы комбинаторики» по учебнику Алгебра 9 класс, Ю.Н. Макарычев и др. Москва. «Просвещение», 2011 год

Глава 5 Элементы комбинаторики и теории вероятностей

§11 Элементы комбинаторики

30.Примеры комбинаторных задач

31. Перестановки

32. Размещения

33. Сочетания

§12. Начальные сведения из теории вероятностей

34. Относительная частота случайного события

35. Вероятность равновозможных событий

Для тех, кто хочет знать больше

36. Сложение и умножение вероятностей

Задачи простого уровня сложности на прямое использование формул комбинаторики, или на перебор возможных вариантов: №714-717, №№726-728, №№732-736, №№754-759, №№768-771, №№831-835.

Второй уровень подразумевает выполнение двух и более действий при решении задачи: №№718-725, №№737-743, №№746-750, №№760-764, №772, №776, №779, №780, №836, №838, №839, №№841-844, №846, №849, №852.

Третий уровень- обратная задача, прикладные задачи №781, №782, №837, №840, №845, №847, №848, №850, №851, №853, №854, №855.

ГЛАВА 2 Организация обучения теме «Элементы комбинаторики»

§ 3 Перечень познавательных УУД при обучении теме: «Элементы комбинаторики»

1.1 познавательные общеучебные действия:

1.1.0 принятие и сохранение учебной задачи

1.1.2 поиск необходимой информации и её понимания

1.1.4 выполнение знаково-символических действий

1.1.6 Построение речевых высказываний

1.2 познавательные логические учебные действия:

1.2. подведение под понятие

1.2.3 анализ объектов

1.2.8 построение логической цепи рассуждения

§ 4 Краткий конспект темы «Элементы комбинаторки»

Элементы комбинаторики. Размещения, перестановки, сочетания.

Актуализация знаний: Представьте, что у вас чемодан с кодовым замком и вы забыли код. Сколько максимально возможных вариантов вы должны будете перебрать, чтобы угадать код из четырёх цифр?

Точно ответить на этот вопрос мы сможем в конце урока.

В науке и на практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций, такие задачи получили название комбинаторных задач, а раздел математики, в котором рассматриваются подобные задачи, называют комбинаторикой.

При решении задач комбинаторики используют следующие правила:

Правило суммы.

Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

Правило произведения.

Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m*n способами.

Определение. Факториалом натурального числа n называется произведение всех чисел от 1 до n:

Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.

Определение. Размещениями из n элементов по k элементов называются группы, составленные из данных n элементов, содержащие в каждой по k элементов и отличающиеся одна от другой либо самими элементами, либо их порядком.

кол-во размещений из n элементов по k элементов

Определение. Перестановками из n элементов называются группы, составленные из данных n элементов, содержащие в каждой по n элементов и отличающиеся одна от другой только порядком элементов.

кол-во перестановок из n элементов

Определение. Сочетаниями из n элементов по k элементов называются группы, составленные из данных n элементов, содержащие в каждой по k элементов и отличающиеся одна от другой только самими элементами.

кол-во сочетаний из n элементов по k элементов

З а м е ч а н и е. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n₁ элементов одного вида, n₂ элементов другого вида и т.д., то число перестановок с повторениями

P_n (n₁, n₂, ...) = n! / (n₁! n₂! ... ), где n₁ + n₂ + ... = n.

§ 5 Карта изучения темы «Элементы комбинаторики»

1

2

3

4

5

6

7

8

Ц 1,5

Ц 1 -3

Ц 1 -3

Ц 1- 3

Ц 1- 3

Ц 2 -4

Ц 2-5

Ц 2,3,4,5

П. 30

П. 31

П. 31-32

П. 31-32

П. 33

П.31-33

П. 31-33 обобщ.урок

С.Р

II. Блок актуализации знаний учащихся

Знать: Знать факториал числа, формулы перестановок, сочетаний, размещений, правила суммы и произведения, план решения комбинаторной задачи Уметь: находить факториал числа, выполнять преобразования дробей с факториалами, вычислять по формулам перестановки, размещения, сочетания, используя правило суммы и произведения.

III. Предметные результаты (Ц 2, 3 таблицы целей): уметь решать комбинаторные задачи, используя понятия: число комбинаций (число способов), способы рассуждений (перебор возможных вариантов)

YI. Образцы заданий итоговой контрольной работы (Ц 5)

Y. Средства обучения теме

1 уровень

Баллы

2 уровень

Баллы

3 уровень

Баллы

Задача.1. Сколько можно записать четырехзначных чисел, используя без повторения все 10 цифр?

Задача.2. Пусть имеется множество, содержащие 4 буквы: {А,В,С,Д}. Записать все возможные сочетания из указанных букв по три

Задача.3. Сколькими способами можно расставить 9 различных книг на полке, чтобы определенные 4 книги стояли рядом?

Задача.4. Нужно выбрать в подарок 4 из 10 имеющихся книг. Сколькими способами это можно сделать?

1

1

1

1

Задача.1. Имеется 10 белых и 5 черных шаров. Сколькими способами можно выбрать 7 шаров, чтобы среди них были 3 черных.

Задача.2. Сколькими способами можно группу из 12 человек разбить на 2 подгруппы, в одной из которых должно быть не более 5, а во второй – не более 9 человек.

Задача.3. Десять команд участвуют в разыгрывание первенства по футболу, лучшие из которых занимают 1-е, 2-е и 3-е места. Две команды, занявшие последние места не будут участвовать в следующем таком же первенстве. Сколько разных вариантов результата первенства может будут учитывать, если только положение первых трех и последних 2-х команд?

1

2

2

Задача.1. Сколько существует вариантов опроса 11 учащихся на одном занятии, если ни один из них не будет вызван дважды и на занятии может будет опрошено любое количество учащихся, порядок опроса не важен.

Задача 2. Трое юношей и две девушки решили после окончания школы поступить на работу в своём родном городе. В городе имеется 3 завода, на которые набирают только мужчин, два, где нужны только женщины, и два, которые принимают на работу и мужчин и женщин. Сколькими способами пять выпускников могут распределиться на работу?

Задача 3. Сколько пятизначных чисел можно образовать из цифр 1,2 и 3, если допускается повторение этих цифр?

Задача 4. На вечер пришли десять одиннадцатиклассников, девять десятиклассников и восемь десятиклассников. Сколькими способами из них можно составить команду из шести человек (по 2 человека от каждого класса)?

2

2

1

2

1) план решения комбинаторной задачи 2) приём составления задач: cоставление математической модели данной прикладной задачи ([3] стр.186)

YI. Задания для внеаудиторной самостоятельной работы (Ц 2, 3, 5)

1 уровень (обязательный уровень стандарта): №717, №728, №736, №759, № 771, № 835

2 уровень: №№725, 743, 750, 764, 780, 836, 83, 844

3 уровень: №№773, 744, 745, 774, 775, 777, 778

4 уровень: №№ (со звёздочкой ) 781, 782, 837, 840, 845, 84, 848, 850, 851, 853, 854, 855

YII. Темы индивидуальных заданий (Ц 5)

1)История развития теории вероятностей. 2)Комбинаторика: история и современность. 3) Олимпиадные задачи на перебор возможных вариантов. 4) Самостоятельно выбранная тема.

YIII. Метапредметные результаты: перечень учебных действий (умений) для освоения темы (Ц 1 - 5)

Познавательные УУД

Регулятивные УУД

Коммуникативные УУД

Личностные УУД

Обобщение, конкретизация, анализ;

постановка и решение проблемы при составлении задачи

Выбор и принятие целей, составление плана, самоконтроль, самооценка, соотнесение своих знаний с той учебной информацией, которую нужно усвоить;

приёмы саморегуляции

Взаимоконтроль, взаимопроверка, распределение обязанностей в группе, умение слушать, выступать, рецензировать, писать текст выступлений

Рефлексия собственной деятельности

§ 6 Таблица целей обучения теме «Элементы комбинаторики»

Формулировки обобщённых целей

Формулировки учебных задач, с помощью которых достигается обобщённая цель

Средства помощи

цель считается достигнутой, если Вы на уровнях:

первом

втором

третьем

Ц 1: приобретение УИ, формирование логических ПУД

а) сравниваете решение однотипных задач б) решаете задачи перебором возможных вариантов б) делаете выбор формулы используя помощь;

а) обобщаете решение задач одного типа; б) составляете приёмы их решения с помощью подсказки

а) составляете приёмы решения типов задач самостоятельно или по плану; б) выполняете анализ и выявляете формулы, нужные для решения комбинаторной задачи, в) комбинируете формулы для решения задачи г) составляете приёмы решения с помощью указаний

а) карточки- информаторы; б) подсказки (план решения задачи); в) образцы записей решений задач в учебнике и тетради

Ц 2: кон-троль усвоения теории при работе с классами и типами задач

первом

втором

третьем

знаете а) определения: 1) факториала числа; 2) перестановки; 3) размещения 4) сочетания; 5) правила суммы; 6) правила произведения; б) приводите примеры в соответствии с определениями; 3) используете предписания для решения задач

знаете определения; понимаете какой формулой необходимо воспользоваться при прочтении задачи и как отобрать нужные комбинации; приводите примеры в соответствии с определениями;

знаете 1) приём отбора нужной формулы; 2) понимаете значение комбинаторных задач в разных областях науки

Ц 3: применение знаний и умений при решении задач

первом

втором

третьем

умеете: использовать основные формулы для решения простейших комбинаторных задач

умеете: а) использовать формулы комбинаторики для для решения задач 2-го уровня сложности;

умеете а) использовать основные формулы комбинаторики и их комбинации для решения задач 3-го уровня сложности; б) решать задачи 3-го уровня сложности; в) использовать формулы для решения прикладных задач

Ц 4: формирование КУД

Ц 4: а) работаете в группе, оказываете взаимопомощь, рецензируете ответы товарищей; б) организуете взаимоконтроль, взаимопроверку и др. на всех этапах учебно-познавательной деятельности (УПД) по выполненным заданиям предыдущих уровней с обоснованием; в) оказываете помощь, работающим на предыдущих уровнях; г) осуществляете поиск информации для подготовки письменного сообщения и устного выступления в соответствии с изучаемой темой, используя правила коммуникативного взаимодействия

приёмы контроля, решения задачи, рецензирования, оценки; таблица коммуникативной компетентности

Ц 5: формирование общих ПУД и РУД

Ц 5: а) выбираете уровни достижения целей и формулируете цели своей учебной деятельности; б) выбираете задачи и решает их; в) осуществляете самопроверку с использованием образцов, приёмов; г) составляете контрольную работу для своего уровня усвоения; д) оцениваете свою итоговую деятельность по данным объективным критериям; по собственным критериям, сравнивая их с объективными критериями; е) делаете выводы о дальнейших действиях, планируете коррекцию учебно-познавательной деятельности

Приёмы выбора и рефлексии достижения целей, саморегуляции (диагностики и коррекции) УПД

§ 7 Тематический план темы: «Элементы комбинаторики»

№ уро-

ков

Раздел, тема урока

Форма урока; форма обучения

Предметные и метапредметные результаты

Ц 1 (ПЛ УУД), Ц 2 (ПО УУД, РУУД), Ц 3 , Ц 4 (КсУУД, КРУУД), Ц 5 (ПОУУД, РУУД)

1 - 8

Название темы

Элементы комбинаторики

Средства обучения

1)план решения комбинаторной задачи; 2) приём составления задач: cоставление математической модели данной прикладной задачи ([3] стр.186) ;

4) Карта темы

Уроки: лекция, практикум.

Фронтальная, индивидуальная

групповая

формы обучения

Ц 1: приобретение учебной информации и развитие интеллектуальных умений при изучении: а) понятий; б) типов задач

Ц 2: контроль усвоения теоретических знаний: а) математических понятий; в) типов и классов задач

Ц 3: применение знаний и интеллектуальных умений при решении математических и учебных задач

Ц 4: развитие коммуникативных умений через: включение в групповую работу; взаимопомощь, рецензирование ответов; организацию взаимоконтроля и взаимопроверки на всех этапах УПД

Ц 5: развитие организационных умений (целеполагание, планирование, реализация плана, саморегуляция УПД

Примеры комбинаторных задач

П.30

Инструктивная лекция

Урок смешанного типа

Фронтально-индивидуальная

Ц 5: Введение в тему, постановка и формулирование целей своей учебной деятельности;

Ц 1: Развитие познавательных логических УУД

Перестановки

П.30,31

Урок смешанного типа

Фронтально-индивидуальная

Ц 1: Развитие познавательных логических УУД

Ц 2: 1) понимает разницу между размещениями и сочетаниями, 2) выбирает для решения нужную формулу (комбинацию формул) переходит от одной модели к другой; 3) выполняет преобразования

Ц 3:

Перестановки. Размещения

П.31, 32

Урок смешанного типа

Фронтально-индивидуальная

Ц 1: Развитие познавательных логических УУД

Ц 2: контроль усвоения изученного материала в процессе чтения лекции

Ц 3:

Перестановки. Размещения

П.31, 32

Практикум:

Фронтальная и парная формы

Постановка и решение проблемы (познавательные УУД)

Ц 1: составление плана и схем решения задачи; составление предписаний;

Ц 3

Сочетания

П.33

Урок смешанного типа

Фронтально-индивидуальная

Ц1

Ц 2: находит ошибки в решении задач своего уровня сложности; решает задачи своего уровня сложности;

Ц 3:

Решение задач

П. 31-33

Практикум

Фронтально-индивидуальная, индивидуальная или парная

Ц 2, 3: использует предписания для решения типов задач своего уровня сложности, составляет задачи, аналогичные данным, обратные задачи и решает их;

Ц 4: в соответствии таблицей целей;

Обобщающий урок

Ц 2 - 5

Решение разных задач по теме: С.Р.

Практикум.

Индивидуальная

Ц 2, 3, 4, 5: выбирает задачи своего уровня сложности , решает их, осуществляет самопроверку; делает выводы о качестве собственных знаний, необходимых для выполнения контрольной работы

Внеурочная самостоятельная деятельность:

I. Тематика для подготовки рефератов(по итогам изучения темы) 1)Предмет теории вероятностей. 2) История развития теории вероятностей. 3) Комбинаторика: история и современность. 4) Комбинаторные задачи 5) История комбинаторики 6) Олимпиадные задачи на перебор возможных вариантов. 7) Самостоятельно выбранная тема.

§ 8 Средства обучения теме «элементы комбинаторики»

План решения комбинаторной задачи (подсказка 1 уровня):

Определить, можно ли сразу посчитать комбинации, или необходимо произвести отбор.
Определить: составляется пребор вариантов (перестановки) или подмножества данного множества (размещения, сочетания)
Определить порядок следования элементов важен (размещения) или неважен (сочетания).

формулы комбинаторики, правила суммы и произведения, образцы записей решений задач в учебнике.

§ 9 Фрагмент урока «Комбинаторные задачи»

ТЕМА: Комбинаторные задачи

ЦЕЛИ: Расширение понятийной базы. Формирование умения самостоятельно строить и применять новое знание

ФОРМА УРОКА: Урок усвоения новой учебной информации

СРЕДСТВА ОБУЧЕНИЯ:

Приём составления задач: cоставление математической модели данной прикладной задачи ([3] стр.186), план решения комбинаторной задачи (подсказка 1 уровня), формулы комбинаторики, правила суммы и произведения, образцы записей решений задач в учебнике.

ХОД УРОКА.

Мотивация учебной деятельности (Познавательные общеучебные УУД: 1.1.0 принятие и сохранение учебной задачи, Коммуникативные УУД 2.1.1 планирование учебного сотрудничества с учителем и сверстниками )

2. Этап актуализации и пробного учебного действия

Цель: подготовка мышления учащихся и осознание ими потребности к выявлению причин затруднений в собственной деятельности.

организация повторения и знаковая фиксация способов действий, запланированных для рефлексивного анализа учащимися, - определений, алгоритмов;
активизация соответствующих мыслительных операций и познавательных процессов (внимание, память);

Основные элементы комбинаторики. СЛАЙД 1-2.

Размещение

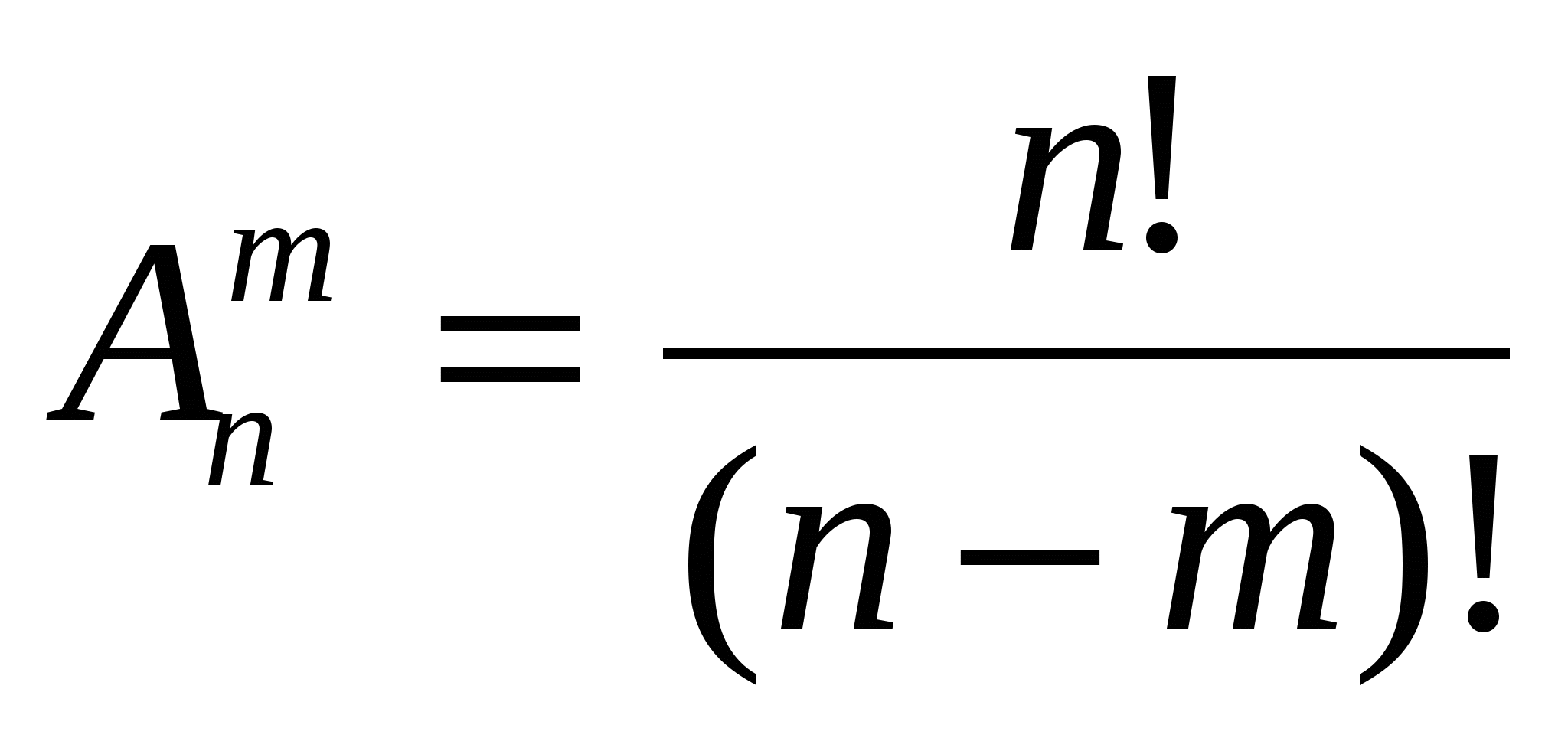
Это любое упорядоченное подмножество m из элементов множества n.

Перестановки (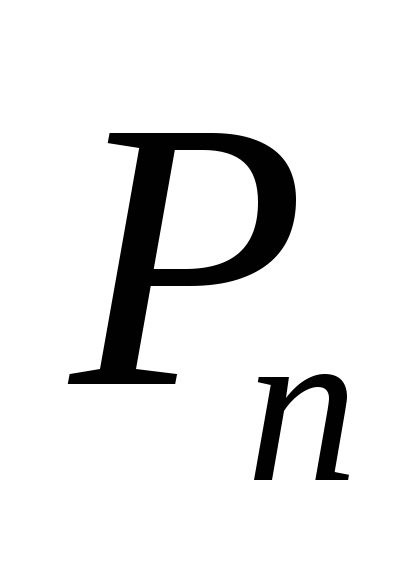). Если m = n, то эти размещения называются перестановками.

Сочетания (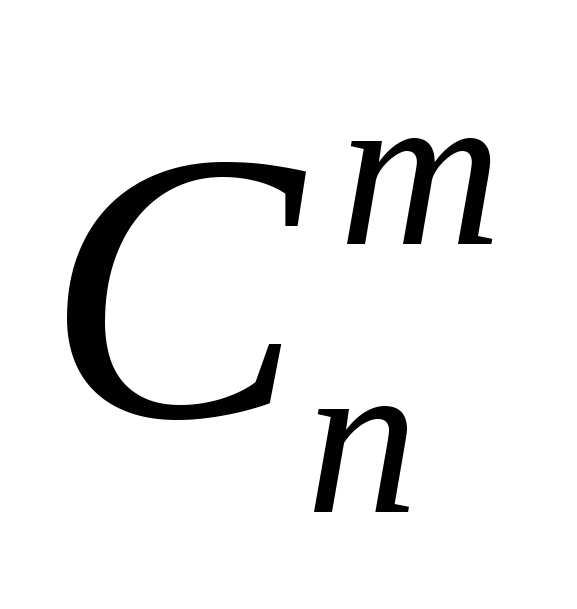) – это любое подмножество из m – элементов, которые принадлежат множеству, состоящему из n – различных элементов.

Следствие. Число сочетаний из n элементов по n – m равно число сочетаний из n элементов по m, т.е. .

3. Организация мотивирования («хочу» - «надо» - «могу») и выполнение учащимися работы на применение способов действий, запланированных для рефлексивного анализа;

(Познавательные общеучебные УУД 1.1.5 выбор эффективных способов решения задач в зависимости от конкретных условий, Познавательные логические УУД 1.2.8 построение логической цепи рассуждения, Коммуникативные УУД 2.2.1 строить монологические высказывания в устной форме, 2.2.6 взаимоконтроль, взаимооценка УПД, Регулятивные УУД 3.3 соотнесение выявленной учебной информации с собственными ЗиУ; принятие решения об использовании помощи, 3.7 самодиагностика и коррекция собственных учебных действий)

План решения комбинаторной задачи (подсказки 1 уровня):

Определить можно ли сразу посчитать комбинации, или необходимо произвести отбор.
Определить: составляется пребор вариантов (перестановки) или подмножества данного множества (размещения, сочетания)
Определить порядок следования элементов важен (размещения) или неважен (сочетания).

В размещении учитывается порядок элементов при выборе, а в сочетаниях – не учитывается.

Практическая работа.

Задача.1. Сколько можно записать четырехзначных чисел, используя без повторения все 10 цифр?

Решение:

1) .

2) т.к. есть среди чисел 0, который не может стоять впереди, поэтому надо еще найти .

3) .

Задача.2. Пусть имеется множество, содержащие 4 буквы: {А,В,С,Д}. Записать все возможные сочетания из указанных букв по три.

Решение: Таких сочетаний будет 4: АВС; АСД; АВД; BCД. Здесь в число сочетаний не включены, например АВС, ВСА, т.к. у нас уже есть АВС, потому что порядок элементов в сочетании не учитываются.

Задача.3. Сколькими способами можно расставить 9 различных книг на полке, чтобы определенные 4 книги стояли рядом?

Решение: если обозначить 4 определенные книги как одно целое, то получается 6 книг, которые можно переставлять.

переставляются, 4 определенные книги можно переставлять . Тогда всего перестановок по правилу умножения будет

Задача.4. Нужно выбрать в подарок 4 из 10 имеющихся книг. Сколькими способами это можно сделать?

Решение:

Задача.5. Имеется 10 белых и 5 черных шаров. Сколькими способами можно выбрать 7 шаров, чтобы среди них были 3 черных.

Решение: .

Белые шары

Черных шаров

Тогда

Организация самопроверки учащимися своих работ по готовому образцу с фиксацией полученных результатов (без исправления ошибок) (Регулятивние УУД: волевая саморегуляция).

Задача.6. Сколькими способами можно группу из 12 человек разбить на 2 подгруппы, в одной из которых должно быть не более 5, а во второй – не более 9 человек.

Решение:

Первая подгруппа может состоять либо из 3, либо из 4, либо из 5 человек.

, , , .

Задача.7. Десять команд участвуют в разыгрывание первенства по футболу, лучшие из которых занимают 1-е, 2-е и 3-е места. Две команды, занявшие последние места не будут участвовать в следующем таком же первенстве. Сколько разных вариантов результата первенства может будут учитывать, если только положение первых трех и последних 2-х команд?

Решение: 1-е три места может будут распределены: способов.

Остается 7 команд, две из которых выбывают из следующего первенства т.к. порядок выбывших команд не учитывается => способом.

Тогда число возможных результатов = .

Задача.8. Сколько существует вариантов опроса 11 учащихся на одном занятии, если ни один из них не будет вызван дважды и на занятии может будет опрошено любое количество учащихся, порядок опроса не важен.

Решение:

может не спросить ни одного, т.е. ,
если только 1, то ,

если только 2-х то и т.д.

Тогда он всего опросит

СПИСОК ЛИТЕРАТУРЫ

Программа (фрагмент) М.В. Васильева
Алгебра 9. Учебник для общеобразовательных учреждений Ю.Н. Макарычев и др.(под редакцией С.А.Теляковского) М. «Просвещение» 2011
Л.И.Боженкова Методика формирования универсальных учебных действий при обучении геометрии, М. БИНОМ. Лаборатория знаний, 2013
Лекции КПК «Актуальные проблемы развития профессиональной компетентности учителя математики (в условиях реализации ФГОС), преподаватель М.В. Васильева, 2013г.
"Комбинаторика и её задачи" . Автор: Паранина Екатерина, Назарова Арина. Руководитель: Зашкалова С.И.2011-2012 учебный год. МБОУ «Илькинская СОШ»
Информационный проект. Авторы проекта: Щербаков Евгений, Новов Максим, Воронцов Денис, Соболева Кристина. Руководитель проекта: Степушкина Н.Ю.
Мордкович А.Г., Семенов П.В. События. Вероятность. Статистика: Дополнительные материалы к курсу алгебры для 7 – 9 кл. – М.:Мнемозина, 2002. (к учебникам А.Г. Мордковича)
Ткачева М.В.,Федорова Н.Е. Алгебра, 7 – 9: Элементы статистики и вероятность. – М.: Просвещение, 2003. (к учебникам А.Ш. Алимова и др.)
Бунимович Е.А., Булычев В.А. Вероятность и статистика, 5 – 9 кл. – М.: Дрофа, 2002.
О.Б. Богомолова. Логические задачи. – М. Бином, 2006. – 270 с.
Федеральный государственный образовательный стандарт общего основного образования / М-во образования и науки Рос. Федерации. – М.: Просвещение, 2011. – 48 с
Асмолов А.Г. Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособие для учителя/под ред. А.Г. Асмолова. – М.: Просвещение, 2010. – 159 с.
Данилюк А.Я., Кондаков А.М., Тишков В.А.. Концепция духовно-нравственного развития и воспитания личности гражданина России. – М.: Просвещение, 2009. – 24 с.
Примерные программы по математике. – М.: Просвещение, 2010. – 67 с.

ПРИЛОЖЕНИЕ 1 Список универсальных учебных действий (УУД)

Название УУД

Условное сокращение

Познавательные УУД

ПОД 1

Познавательные общеучебные действия

1.1 – 1.3

1.1.0 принятие и сохранение познавательной цели (учебной задачи);

1.1.1.самостоятельное выделение и формулирование познавательной цели (учебной задачи);

1.1.2.поиск необходимой информации и её понимание (смысловое чтение, определение основной и второстепенной информации);

1.1.3 структурирование информации и знаний (в т.ч. составление текстов) и её понимание;

1.1.4 выполнение знаково-символических действий (в т.ч. моделирования);

1.1.5 выбор эффективных способов решения задач в зависимости от конкретных условий;

1.1.6 построение речевых высказываний в устной и письменной формах (подробный и сжатый пересказ текста);

1.1.7 рефлексия способов и условий действия;

1.1.8 самоконтроль и самооценка процесса и результатов деятельности;

1.1.0

1.1.1

1.1.2

1.1.3

1.1.4

1.1.5

1.1.6

1.1.7

1.1.8

Познавательные логические учебные действия

1.2

1.2.1 сравнение; 1.2.2 подведение под понятие; 1.2.3 анализ объектов для выделения свойств и признаков объектов; 1.2.4 синтез (в т.ч. самостоятельное достраивание, восполнение недостающих компонентов); 1.2.5 выведение следствий; 1.2.6 сериация и классификация; 1.2.7 установление причинно - следственных связей; 1.2.8 построение логической цепи рассуждения; 1.2.9 доказательство

1.2.1.- 1.2.9

Познавательное действие «Постановка и решение проблем»

1.3

1.3.1 формулирование проблемы; 1.3.2. выдвижение гипотез и их обоснование; 1.3.3 самостоятельное создание способов решения проблем творческого и поискового характера

1.3.1 – 1.3.3.

Коммуникативные УУД

2.1. Действия для осуществления совместной деятельности (в т.ч. работа в группе)

2.1.

2.1.1 планирование учебного сотрудничества с учителем и сверстниками;

2.1.2 инициативное сотрудничество в поиске и сборе информации;

2.1.3 разрешение конфликтов – выявление проблемы конфликта, поиск способов устранения, принятие решения и его реализация;

2.1.4 управление поведением партнёра – контроль, коррекция, оценка действий партнёра;

2.1.1

2.1.2

2.1.3

2.1.4

2.2. Действия для осуществления общения и взаимодействия

2.2

2.2.1. строить монологические высказывания в устной форме (достаточно полно и точно выражать свои мысли в соответствии с задачами и условиями коммуникации);

2.2.2 слушать и понимать сообщать мнения и взгляды других (высказанные в устной и письменной формах);

2.2.3 сообщать в устной и письменной формах мнения и взгляды других;

2.2.4 использовать речевые средства для дискуссии и аргументации своей позиции;

2.2.5 владеть монологической и диалогической формами речи в соответствии с нормами родного языка

2.2.6 взаимоконтроль, взаимооценка УПД

2.2.1

2.2.2

2.2.3

2.2.4

2.2.5

2.2.6

3. Регулятивные УУД