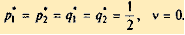
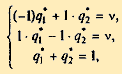
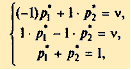
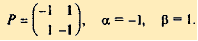
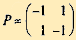
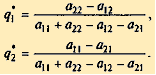
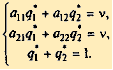
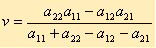
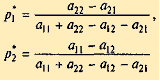
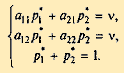
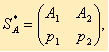
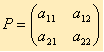
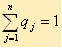
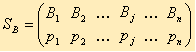
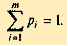
Решение игр в смешанных стратегиях.

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решения игры. Так, в примере 1 α ≠ β, седловая точка отсутствует. В таком случае можно получить оптимальное решение, случайным образом чередуя чистые стратегии.

Смешанной стратегией S_A игрока А называется применение чистых стратегий A₁, A₂, ..., A_m с вероятностями p₁, p₂, ..., p_i, ..., p_m причем сумма вероятностей равна 1:

Смешанные стратегии игрока А записываются в виде матрицы

или в виде строки S_A = (p₁, p₂, ..., p_i, ..., p_m)

Аналогично смешанные стратегии игрока В обозначаются:

, или, S_B = (q₁, q₂, ..., q_i, ..., q_n),

где сумма вероятностей появления стратегий равна 1:

Чистые стратегии можно считать частным случаем смешанных и задавать строкой, в которой 1 соответствует чистой стратегии. На основании принципа минимакса определяется оптимальное решение (или решение) игры: это пара оптимальных стратегий S^*_A , S^*_B в общем случае смешанных, обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей. Выигрыш, соответствующий оптимальному решению, называется ценой игры v. Цена игры удовлетворяет неравенству:

α ≤ v ≤ β

где α и β — нижняя и верхняя цены игры. Справедлива следующая основная теорема теории игр — теорема Неймана. Каждая конечная игра имеет по крайней мере одно оптимальное решение, возможно, среди смешанных стратегий. Пусть S^*_A = (p^*₁, p^*₂, ..., p^*_i, ..., p^*_m) и S^*_B = (q^*₁, q^*₂, ..., q^*_i, ..., q^*_n) — пара оптимальных стратегий. Если чистая стратегия входит в оптимальную смешанную стратегию с отличной от нуля вероятностью, то она называется активной.

Справедлива теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры v, если второй игрок не выходит за пределы своих активных стратегий.

Эта теорема имеет большое практическое значение — она дает конкретные модели нахождения оптимальных стратегий при отсутствии седловой точки.

Рассмотрим игру размера 2×2, которая является простейшим случаем конечной игры. Если такая игра имеет седловую точку, то оптимальное решение — это пара чистых стратегий, соответствующих этой точке.

Игра, в которой отсутствует седловая точка, в соответствии с основной теоремой теории игр оптимальное решение существует и определяется парой смешанных стратегий S^*_A = (p^*_1, p^*₂) и S^*_B = (q^*₁, q^*₂).

Для того чтобы их найти, воспользуемся теоремой об активных стратегиях. Если игрок А придерживается своей оптимальной стратегии S'_A, то его средний выигрыш будет равен цене игры v, какой бы активной стратегией ни пользовался игрок В. Для игры 2×2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Выигрыш игрока А (проигрыш игрока В) — случайная величина, математическое ожидание (среднее значение) которой является ценой игры. Поэтому средний выигрыш игрока А (оптимальная стратегия) будет равен v и для 1-й, и для 2-й стратегии противника.

Пусть игра задана платежной матрицей

Средний выигрыш игрока А, если он использует оптимальную смешанную стратегию

,

а игрок В — чистую стратегию B₁ (это соответствует 1-му столбцу платежной матрицы Р), равен цене игры v: a₁₁ p^*₁+ a21 p^*₂= v. Тот же средний выигрыш получает игрок А, если 2-й игрок применяет стратегию B₂, т.е. a₁₂ p^*₁+ a₂₂ p^*₂= v. Учитывая, что p^*₁+ p^*₂= 1, получаем систему уравнений для определения оптимальной стратегии S'_A и цены игры v:

Решая эту систему, получим оптимальную стратегию

и цену игры

Применяя теорему об активных стратегиях при отыскании S^*_B- оптимальной стратегии игрока В, получаем, что при любой чистой стратегии игрока А (А₁ или А₂) средний проигрыш игрока В равен цене игры v, т.е.

Тогда оптимальная стратегия определяется формулами:

Пример 1.

Игра «поиск»

Игрок А может спрятаться в одном из двух убежищ (I и II); игрок В ищет игрока А, и если найдет, то получает штраф 1 ден. ед. от А, в противном случае платит игроку А 1 ден. ед. Необходимо построить платежную матрицу игры.

Решение. Для составления платежной матрицы следует проанализировать поведение каждого из игроков. Игрок А может спрятаться в убежище I – обозначим эту стратегию через A₁ или в убежище II — стратегия A₂ .

Игрок В может искать первого игрока в убежище I — стратегия B₁ , либо в убежище II — стратегия B₂. Если игрок А находится в убежище I и там его обнаруживает игрок В, т.е. осуществляется пара стратегий (A₁, B₁), то игрок А платит штраф, т.е. a₁₁ = - 1. Аналогично получаем a₂₂ = - 1 (A₂, B₂). Очевидно, что стратегии (A₁, B₂) и (A₂, B₁) дают игроку А выигрыш 1, поэтому a₁₂ = a₂₁ = 1. Таким образом, для игры "поиск" размера 2×2 получаем платежную матрицу

Применим полученные результаты для отыскания оптимальных стратегий для игры, рассмотренной в примере 1.

Пример 2.

Найти оптимальные стратегии игры, приведенной в примере 1.

Решение. Игра "поиск" задана платежной матрицей без седловой точки:

Поэтому ищем решение в смешанных стратегиях; для игрока А средний выигрыш равен цене игры v (при B₁ и B₂); для игрока В средний проигрыш равен цене игры v (при A₁ и B₂). Системы уравнений в данном случае имеют вид:

Решая эти системы, получаем

Это означает, что оптимальная стратегия каждого игрока состоит в том, чтобы чередовать свои чистые стратегии случайным образом, выбирая каждое из убежищ с вероятностью 1/2, при этом средний выигрыш равен 0.

РЕФЕРАТ ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»

НА ТЕМУ: «Решение игры в смешанных стратегиях».