Министерство Образования Республики Саха (Якутия)

МУ «Аллайховское улусное (районное) управление образования»
МОУ «Чокурдахская средняя общеобразовательная школа имени А.Г. Чикачёва.»

Статья

Мини-справочники для подготовки к ЕГЭ по математике в 11 классе (часть1-В1-В5)

Автор: Кочкина Е.Н.,

учитель математики,

категория: высшая.

Пед. стаж: 32 год.

п. Чокурдах. 2012г.

Мини-справочники для подготовки к ЕГЭ по математике в 11 классе (часть 1-В1-В5)

Кочкина Елена Николаевна,

учитель математики МОУ «Чокурдахская СОШ имени А.Г.Чикачёва», п.Чокурдах, Республика Саха (Якутия).

Одна из причин низких баллов ЕГЭ - отсутствие системы в подготовке учащихся к этой форме итоговой аттестации, а также качественного повторения.

Опыт подготовки к ЕГЭ показал, что без чёткой целенаправленной и систематической работы над повторением теории, применением этой теории на практике, нельзя успешно сдать этот непростой экзамен.

Продолжая статьи про ЕГЭ о применение информационных карт, в этой статье речь пойдет о мини-справочниках. Особенно они нужны для подготовки учащихся не склонных к математике, так называемых «слабеньких», которым как никому другому нужна уверенность, что и они преодолеют «порог ЕГЭ».

Задание В1.1 Округление с недостатком

Теория

Практика

Полезно вспомнить:

При чтении любой задачи нужно ясно представлять описываемую ситуацию,

Деление с остатком.

а = вс + d, а - делимое, в –делитель, с - неполное частное, d – остаток. Пример: 23 = 5 · 4 + 3. Здесь 3 – остаток. 

Округление с недостатком: если надо найти количество предметов, купленных на заданную сумму, или количество цветов в букете, или предметов в определенных условиях.

1. Сырок стоит 7 руб. 20 коп. Какое наибольшее число сырков можно купить на 60 рублей?

Решение: 7 руб. 20 коп =720 коп. 60руб.=6000 коп.

6000 : 720=8(ост.24) ответ: 8.

Или так: Разделим 60 на 7,2: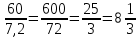

Значит, на 60 рублей можно купить 8 сырков. Ответ: 8

2. Шоколадка стоит 35 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 200 рублей в воскресенье?

Решение: Разделим 200 на 35:

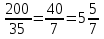
Значит, можно будет купить 5 шоколадок. Еще 2 будут даны в подарок. Всего можно будет получить 7 шоколадок. Ответ: 7

3. На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 30 рублей за штуку. У Вани есть 500 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения?

Решение: Разделим 500:30= 16(ост.2). Но 16 дарить нельзя, значит можно купить 15 тюльпанов. Ответ: 15

4 В университетскую библиотеку привезли новые учебники по геометрии для 1–3 курсов, по 360 штук для каждого курса. Все книги одинаковы по размеру. В книжном шкафу 9 полок, на каждой полке помещается 25 учебников. Сколько шкафов можно полностью заполнить новыми учебниками?

Решение: всего привезли: 360*3=1080 штук.В шкаф помещается 9*25=225. 1080:225= 4(остаток 180) Полностью заполнятся 4 шкафа. Ответ:4

Задание В1.2 Округление с избытком

Теория

Практика

Полезно вспомнить:

При чтении любой задачи нужно ясно представлять описываемую ситуацию,

Деление с остатком.

а = вс + d, а - делимое, в –

делитель, с - неполное частное, d – остаток. Пример: 23 = 5 · 4 + 3. Здесь 3 – остаток. 

Округление с избытком: если надо рассчитать количество чего-либо, которого хватит на сколько-то человек или на определенный период.

Например: 100 : 3 = 33 (остаток 1)

При округлении с избытком получиться 34.

1.Теплоход рассчитан на 500 пассажиров и 15 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?

Решение: 1)500+15 =515 (всего человек)

2) 515: 70= 7(ост.25); значит нужно 8 шлюпок, в 7 по 70 человек, в 1 -25. ответ: 8

2.В пачке 500 листов бумаги формата А4. За неделю в офисе расходуются 1200 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 4 недели?

Решение: За 4 недели в офисе расходуется 1200∙4=4800 листов бумаги. Разделим 4800 на 500; 4800:500 =9(остаток 300). Значит, нужно купить 10 пачек.

Ответ: 10

3. Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?

Решение: Больному нужно выпить 0,5* 3* 21 = 31,5 г лекарства. В одной упаковке содержится 0,5 * 10 = 5 г лекарства. Разделим 31,5:5 =6,3; значит необходимо 7 упаковок. Ответ:7

4. В летнем лагере 218 детей и 26 воспитателей. В автобус помещается не более 45 пассажиров. Сколько автобусов требуется, чтобы перевезти всех из лагеря в город?

Всего в лагере 218 + 26 = 244 чел. Разделим 244 на 45; 244:45= 5 (остаток 19); значит необходимо 6 автобусов. Ответ: 6.

5. В школе есть трехместные туристические палатки. Какое наименьшее число палаток нужно взять в поход, в котором участвует 20 человек?

Решение: Разделим 20 на 3: ; значит необходимо 7 палаток. Ответ:7.

6. В доме, в котором живет Петя, один подъезд. На каждом этаже находится по 6 квартир. Петя живет в квартире № 50. На каком этаже живет Петя?

Решение: Разделим 50 на 6; 50:6 = 8 (остаток 2); значит, Петя живет на 9 этаже. Ответ: 9.

Задание В1.3 Задания на проценты.

Теория

Практика

Задачи на проценты.

1.Процентом называется одна сотая часть величины 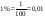. целое составляет 100%.

Например: ; ; .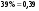

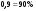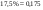2.Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.Например, 125% = 125:100 = 1,25%

3.Чтобы обратить десятичную дробь в проценты, надо ее умножить на 100. Например: 0,971 = 0,971•100 = 97,1%

4.Нахождение процента от числа: чтобы найти процент от числа, надо это число умножить на соответствующую дробь.

Например: а)13% от 50; 1);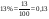

2);

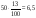б) 20% от 45 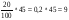кг; (кг)

в) 118% от х ;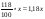

5.Нахождение числа по его проценту: чтобы найти число по его проценту, надо часть, соответствующую этому проценту, разделить на дробь. Например, 8% длины всего отрезка составляет 2,4 см, то длина всего отрезка равна

2,4:0,08=240:8=30 (см)

6.Нахождение процентного отношения чисел: чтобы узнать, сколько процентов одно число составляет от второго, надо первое число разделить на второе и результат умножить на 100. Например, 2 г. соли в растворе массой 50 г. составляет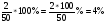

Чтобы записать текст с помощью уравнений:

-Обозначить неизвестную величину переменной

-Выразить через нее другие величины;

-Составить уравнение и решить его.

- При необходимости сделать проверку;

-Оформить ответ.

1. Цена на автобусный билет - 15 рублей. Сколько билетов можно будет купить на 100 рублей после того, как цена на билет будет повышена на 20%?

Решение: 1)Чтобы найти 20% от 15 рублей, нужно 15 рублей разделить на 100 и умножить на 20. (15/100)*20=3. Таким образом, 20% от 15 рублей - это 3 рубля.

2)15+3=18; новая цена на билет составит 18 рублей.

3)определим, сколько билетов по новой цене в 18 рублей можно купить на 100 рублей.

- можно купить 5 билетов (10 рублей - сдача, которой не хватает еще на один билет по 18 рублей). Ответ. 5.

2. Цена на электрический чайник была повышена на 22% и составила 1830 рублей. Сколько рублей стоил товар до повышения цены?

Решение: Пусть чайник стоил х (руб.), тогда после повышения он будет стоить 1,22х, составим уравнение: 1,22х =1830; х= 1830:1,22; х=1500 ; Ответ: 1500

3.Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25%?

Решение: Во время распродажи шампунь станет стоить 160-0,25∙160=120 рублей. Разделим 1000 на 120; 1000:120= (остаток 40); Значит, можно будет купить 8 флаконов шампуня. Ответ: 8

4.Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?

Решение: После повышения цены ручка станет стоить 40+0,1∙40=44 рубля. Разделим 900 на 44; 900:44=20 (остаток 20)

Значит, можно купить 20 ручек. Ответ: 20

Задание В2.1 Определение величины по диаграмме.

Теория

Практика

ДИАГРАММА (от греч. diagramma - изображение, рисунок, чертеж), графическое изображение, наглядно показывающее соотношение каких- либо величин или между значениями одной и той же величины в разные моменты времени.

Виды диаграмм:

круговая (процентная) - где за 100% принята площадь круга; площадная - количества выражены разными по размеру площадями: кругами, секторами, прямоугольниками и т. п.; столбчатая – когда количества выражены столбиками разной высоты;

другие.

1. На диаграмме показана среднемесячная температура воздуха в (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия.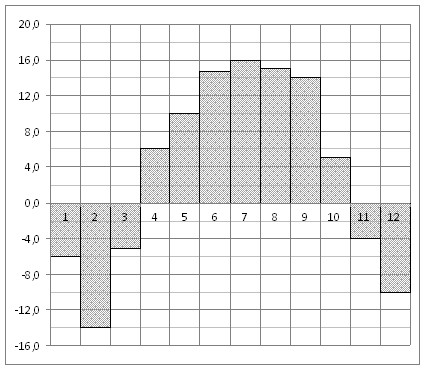

Решение: Из диаграммы видно, что наименьшая среднемесячная температура составляет −14 °C (см. рисунок). Ответ: −14.

2. На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день. Определите по диаграмме, сколько было дней в данный период, когда суточное количество посетителей не превосходило 600 000 человек?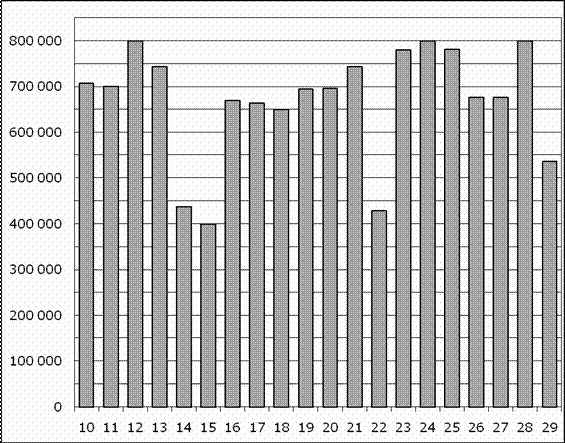

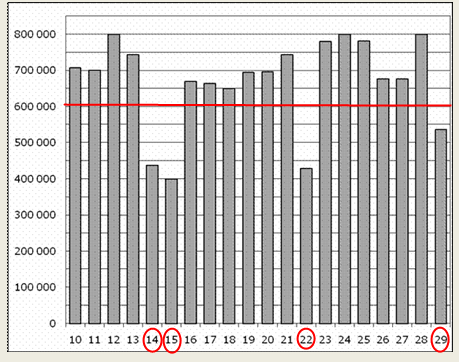
Решение: Рассмотрим график. Проведем уровень на 600 000 человек. Сосчитаем количество столбцов диаграммы, не достающих до уровня (красная линия). Их всего 4.

. Ответ: 4.

Задание В2.2 Определение величины по графику

Теория

Практика

Правило (закон) соответствия между множествами X и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией. Множество X всех допустимых действительных значений аргумента x, при которых функция y = f (x) определена, называется областью определения функции. Множество Y всех действительных значений y, которые принимает функция, называется областью значений функции.

Графиком функции называется множество точек, удовлетворяющих у=f(х).

В большинстве примеров и задач на построение графиков функций вы встречались с такой ситуацией: функция задана формулой, требуется исследовать ее свойства и построить график . Представляет значительный практический интерес другая задача: задан график , с помощью которого требуется перечислить основные свойства этой функции или найти соответствующие значения аргумента или функции..

Подобные задачи часто решаются в ходе экспериментальных исследований. Построение графиков при этом осуществляется разными методами. Например, по точкам, найденным экспериментально.

Для успешного решения задания B2 полезно научиться:
• определять значение функции при различных способах задания функций,
• находить по графику функции наибольшие и наименьшие значения,
• описывать с помощью функций различные зависимости и читать их графики,
• пользоваться информацией, представленной в виде таблиц и графиков.

1.: Дается график, на котором показана температура воздуха в течение трех суток. На одной оси (абсцисс) отмечается время суток, на другой (ординат) – температура в градусах Цельсия. Необходимо определить максимальную температуру 15 августа.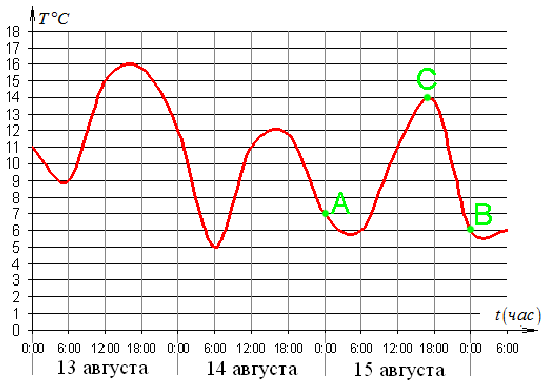

Решение: На первом этапе выделим 15 августа на графике ( это участок AB). Очевидно, что наибольшей температуре в течение суток соответствует наибольшее значение на промежутке AB. Это значение мы отметили буквой C. Наибольшая температура за 15 августа 14 градусов Цельсия. Ответ. 14.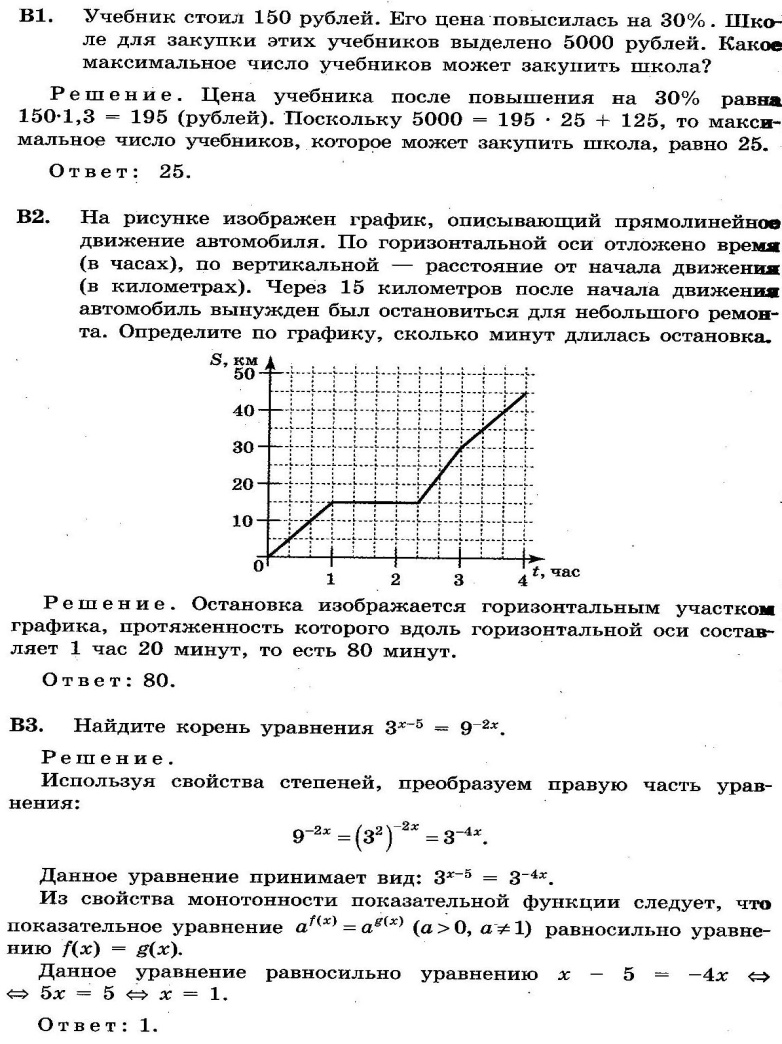

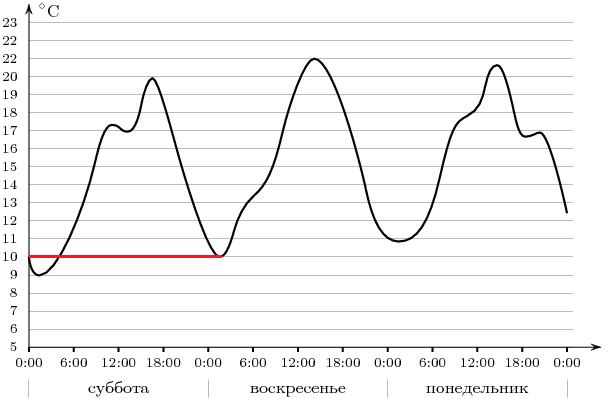
2. На рисунке изображен график, описывающий прямолинейное движение автомобиля. По горизонтальной оси отложено время (в часах), по вертикальной – расстояние от начала движения (в километрах). Через 15 километров после начала движения автомобиль вынужден был остановиться для небольшого ремонта. Определите по графику, сколько минут длилась остановка.

Решение. Остановка изображается горизонтальным участком графика, протяженность которого вдоль горизонтальной оси составляет 1 час 20 минут, то есть 80 минут.

Ответ: 80.

3. На графике показано изменение температуры воздуха в некотором населённом пункте на протяжении трех суток, начиная с 0 часов субботы. На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха в ночь с субботы на воскресенье. Ответ дайте в градусах Цельсия.

Решение: найдём на графике, на оси ОХ время ночи с субботы на воскресенье, наименьшую температуру отметим линией. На оси ОУ получили 10°С.

Ответ: 10°С

Задание В2.3 Вычисления по графику.

Теория

Практика

Для успешного решения задания B2 полезно научиться:
• определять значение функции при различных способах задания функций,
• находить по графику функции наибольшие и наименьшие значения,

• пользоваться информацией, представленной в виде таблиц и графиков.

если необходимо в задаче, надо произвести дополнительные вычисления (например, найти разность или сумму).

1.На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н м. Скорость автомобиля (в км/ч) приближенно выражается формулой v=0,036n, где n — число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был не менее 120 Н м? Ответ дайте в километрах в час.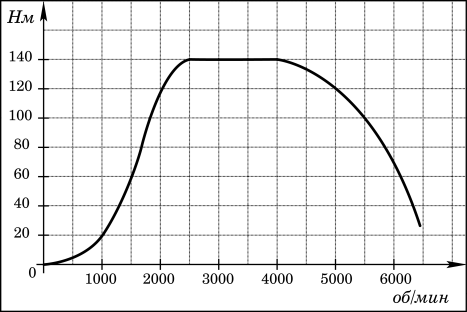

Решение: Для того, чтобы крутящий момент был не меньше 120 Н/ м число оборотов двигателя в минуту n должно быть не меньше 2000 и не больше 5000 (см. график). Поэтому искомая наименьшая скорость определяется по формуле v = 0,036 * 2000 = 72 км/ч. Ответ: 72.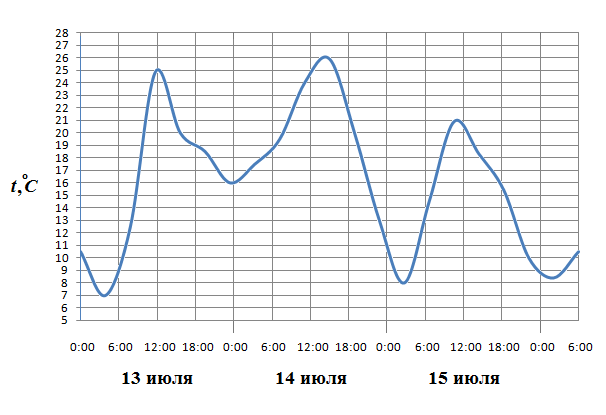

2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурой воздуха 15 июля. Ответ дайте в градусах Цельсия.

Решение:

Из графика видно, что 15 июля наибольшая температура составляла 21 °C, а наименьшая 8 °C. Их разница составляет 13 °C. Ответ: 13.

3. На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами за указанный период. Ответ дайте в градусах Цельсия.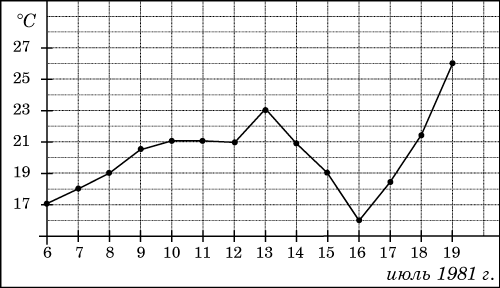

Решение: Из графика видно, что наибольшая и наименьшая температура за указанный период составляла 26 °C и 16 °C соответственно (см. рисунок). Их разность равняется 10 °C.

Ответ: 10.

Задание В3.1 Элементы треугольника

теория

практика

Равносторонний треугольник.

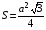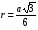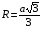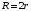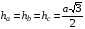; ;; ;_{; где а- сторона; S-площадь; h-высота;} r- радиус вписанной окружности; R- радиус описанной окружности;

p- полупериметр; Р- периметр.

Прямоугольный треугольник.

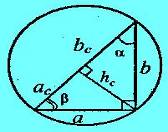
а;в- катеты; с – гипотенуза;

S - площадь., r- радиус вписанной окружности; R- радиус описанной окружности; p- полупериметр; Р- периметр.

; ; ;

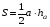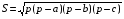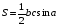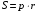
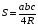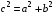: (теорема Пифагора); ;

;

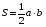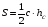
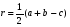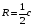
1.Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.

Решение: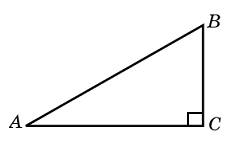

пусть x — меньший катет, тогда x + 2 — больший.

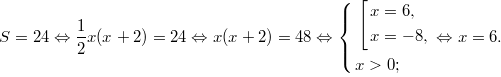
Ответ: 6.

2.Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Найдите боковую сторону треугольника, если его площадь равна 25.

Решение:

Площадь равнобедренного треугольника равна половине произведения квадрата его боковой стороны и синуса угла между боковыми сторонами, следовательно,

где a — искомая боковая сторона треугольника. Поэтому a = 10. Ответ: 10.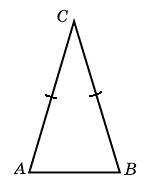

3.Площадь остроугольного треугольника равна 12. Две его стороны равны 6 и 8. Найдите угол между этими сторонами. Ответ дайте в градусах.

Решение:

Ответ: 30.

4. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?

Решение: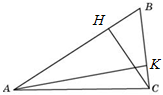

Ответ: 6.

5.Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.

Решение: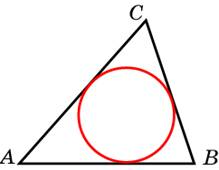

. Ответ: 24.

Задание В3.2 Элементы четырехугольников

Теория

практика

Параллелограмм – это четырёхугольник, противоположные стороны которого попарно параллельны. Любые две противоположные стороны параллелограмма называются его основаниями, а расстояние между ними – высото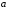й.

и 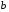– смежные стороны, 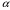– угол между ним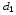и, и 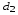– диагонали, 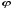– угол между диагоналями, 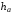– высота, проведенная к стороне 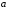, 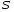– площадь, то: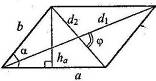

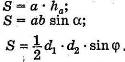
Прямоугольник. Если один из углов параллелограмма прямой, то все остальные углы также прямые. Такой параллелограмм называется прямоугольником  .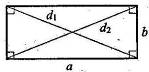

;

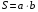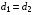
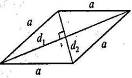
Ромб. Если все стороны параллелограмма равны, то этот параллелограмм называется ромбом; 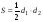; ; 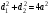Диагонали ромба взаимно перпендикулярны и делят их углы пополам.

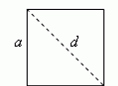
 Квадрат – это параллелограмм с прямыми углами и равными сторонами . Квадрат является частным случаем прямоугольника и ромба одновременно; ; .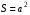

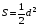Трапеция - это четырёхугольник, у которого две противоположные стороны параллельны .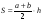; ; 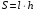; 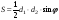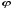– угол между диагоналями. Параллельные стороны называются основаниями трапеции, а две другие – боковыми сторонами. Расстояние между основаниями (h) есть высота. Отрезок l, соединяющий середины боковых сторон, называется средней линией трапеции. Средняя линия трапеции равна полусумме оснований и параллельна им:  Трапеция с равными боковыми сторонами называется равнобочной трапецией. В равнобочной трапеции углы при каждом основании равны .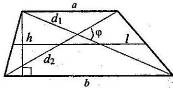

1.Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.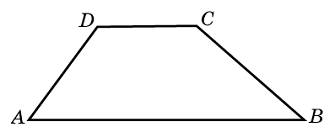

Решение:

.Ответ: 8.

2. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 и 9.

Решение:

Площадь прямоугольника равна произведению длины на ширину, а площадь квадрата равна квадрату его стороны. Поэтому площадь прямоугольника , тогда сторона квадрата будет равна 6Ответ: 6.

3. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.

Решение:

Площадь ромба равна половине произведения его диагоналей. Пусть меньшая из диагоналей равна a, тогда большая равна 3a. Следовательно,

. . а=2 Ответ: 2.

4. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.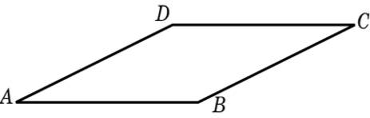

Решение:

Площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание. Пусть высоты равны соответственно a и b. Тогда S = 5 * a = 10 * b = 40. Поэтому a = 8, b = 4. Большая высота равна 8. Ответ: 8.

Задание В3.3 Информационная карта. Площади фигур

Теория

Практика

Формулы площадей

Трапеция

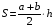
Ромб. ;

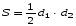Круг

S=

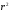
Другие способы решения:

1) Достроить неизвестную фигуру до известной (например: можно достроить четырехугольник до прямоугольника).

2) Разбить неизвестную фигуру на несколько известных (например: можно разбить четырехугольник на два треугольника и прямоугольник).

3) Если d – диагональ квадрата, то его площадь:

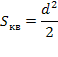
1. Дан четырехугольник, изображенный на клетчатой бумаге. Размер клетки: 1 см х 1 см. Требуется найти площадь четырехугольника.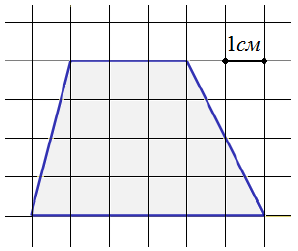

Решение: на рисунке изображена трапеция. Площадь трапеции вычисляется по формуле: где h - высота, a, b - верхнее и нижнее основания. На рисунке видно, что высота трапеции равна 4 см, верхнее основание

3 см, а нижнее 6 см. Тогда по указанной выше формуле находим:

; Ответ. 18.

2. На клетчатой бумаге с клетками размером 1см х 1см изображен треугольник (см. рис.). 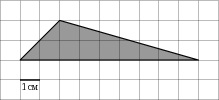Найдите площадь треугольника в квадратных сантиметрах.

Решение. Используем формулу площади треугольника, запишем S =0,5 *2*9=9, т.к. основание треугольника 9 см., высотой является перпендикуляр , проведенный к основанию, он равен 2 см. Тогда площадь треугольника равна S = 9 см²_. Ответ: 9.

3. На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. В ответе запишите .

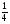Решение: Найдём площадь всего круга, радиусом 3 см. S =*9=9; Заштрихована всего круга; тогда =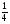* 9: =2,25 ; ответ:2,25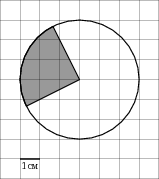

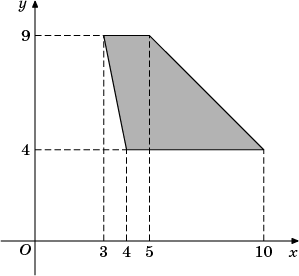
4. Найдите площадь трапеции, вершины которой имеют координаты (4;4), (10;4), (5;9), (3;9).

Решение:

Ответ: 20

Задание В3.4 Элементы окружности и площадь круга.

Теория

Практика

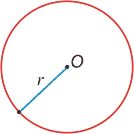
Окружностью называется геометрическая фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки плоскости. Эта точка (О) называется центром окружности. Отрезок, соединяющий любую точку окружности с ее центром, а также его длина, называется радиусом окружности. ОК – радиус.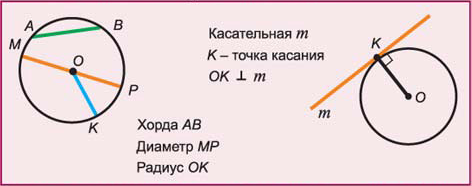

Отрезок, соединяющий две точки окружности, называется хордой (АВ) . Хорда, проходящая через центр окружности, называется диаметром (МР).

Кругом называется фигура, состоящая из всех точек плоскости, расстояние от которых до данной точки не больше данного. Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.

Круговым сектором называется часть круга, лежащая внутри соответствующего центрального угла.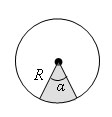

Площадь кругового сектора вычисляется по формуле

Круговым сегментом называется общая часть круга и полуплоскости.

где R – радиус круга, а α - градусная мера соответствующего центрального угла.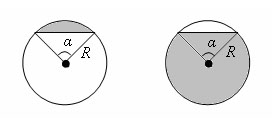

Площадь кругового сегмента, не равного полукругу, вычисляется по формуле

где α - градусная мера соответствующего центрального угла, который содержит дугу этого кругового сегмента, а SΔ – площадь треугольника с вершинами в центре круга и концах радиусов, ограничивающих соответств.-ий сектор. Знак «-» надо брать, когда α < 180°, а знак «+» надо брать, когда α > 180°.

1. Найдите центральный угол сектора круга радиуса , площадь которого равна 1. Ответ дайте в градусах.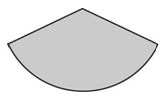

Решение: Площадь сектора круга с дугой n°

Отсюда n° = 360 : 16 = 22,5°. Ответ: 22,5.

2. На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. В ответе запишите .

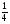Решение: Найдём площадь всего круга, радиусом 3 см. S =*9=9; Заштрихована всего круга; тогда =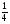* 9: =2,25 ; ответ:2,25

3. На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. В ответе запишите .

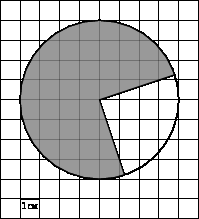
Решение: Площадь фигуры равна трем четвертым площади круга, радиус которого равен 4см. Поэтому

Разделим на пи, получим 12. Ответ: 12

4. Найдите площадь сектора круга радиуса , центральный угол которого равен 90°.

Решение:

Площадь сектора круга с дугой n° равна произведению площади окружности с радиусом R на отношение угла сектора n° к углу полной окружности, т. е. 360°. Поэтому

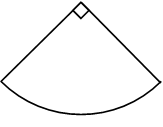
Ответ: 0,25.

Задание В4

Теория

Практика

Полезно вспомнить:

1.Чтобы найти стоимость надо цену товара умножить на количество.

2. Для прямолинейного движения применяют следующие формулы:

S=Vt; V=S: t; t=S:V;

3. Чтобы найти среднюю скорость на участке пути надо

сумму расстояний на участке разделить на затраченное время.

4.При решение задач практической направленности, необходимо продемонстрировать навыки применения математических методов для решения прикладных задач, в том числе социально-экономического и физического характера.

5.Надо правильно интерпретировать полученный результат с учетом жизненных ограничений.

1.Строительная компания должна купить 70 м3 пеноблоков. Имеется три поставщика. Условия доставки и цены даны в таблице. Какая сумма потребуется для самой дешевой покупки с доставкой?

пост

Стоимость пеноблоков (руб. за 1 м3)

Стоимость доставки (в руб.)

Дополнительные условия доставки

1

2600

10000

2

2800

8000

При заказе товара на сумму свыше 150000руб. доставка бесплатная

3

2700

8000

При заказе товара на сумму свыше 200000 руб. доставка бесплатная

Решение: Определим, какую сумму потребуется заплатить каждому.

1 поставщик: 70*2600=182000, то есть, за 70 м3 пеноблоков потребуется заплатить 182000 руб. К этой сумме добавляется стоимость доставки: 182000+10000=192000 рублей. Таким образом, первому поставщику нужно будет заплатить 192000 рублей.

2 поставщик: 70*2800=196000, то есть, за 70 м3 пеноблоков потребуется заплатить 196000 руб. В дополнительном условии сказано, что при покупке товара на сумму свыше 150000 рублей доставка бесплатна. Таким образом, второму поставщику нужно будет заплатить 196000 рублей.

3 поставщик: 70*2700=189000, то есть, за 70 м3 пеноблоков потребуется заплатить 189000 руб. К этой сумме добавляется стоимость доставки: 189000+8000=197000 рублей. Таким образом, третьему поставщику нужно будет заплатить 197000 рублей.

Видно, что дешевле всего - купить пеноблоки у первого поставщика и эта покупка обойдется в 192000 рублей. Ответ. 192000

2. Три туристических маршрута из пункта А в пункт В пролегают через пункты С, D и К. На первом маршруте расстояние от пункта А до пункта С туристы прошли за 6 дней, расстояние от пункта С до пункта В туристы преодолели за 5 дней. На втором маршруте расстояние от пункта А до пункта D туристы прошли за 5 дней, а расстояние от пункта D до пункта В – за 4 дня. На третьем маршруте расстояние от пункта А до пункта К туристы прошли за 4 дня, а расстояние от пункта К до пункта В – за 6 дней. Расстояния между соседними пунктами показаны на схеме. Найдите наибольшую среднюю скорость (в км/день) движения туристов из пункта А в пункт В.

Решение. Путь от пункта А до пункта В, пройденный туристами по первому маршруту, равен 102 + 96 = 198 (км). Этот путь туристы прошли за 11 дней. Таким образом, средняя скорость движения туристов на первом маршруте равна 198:11 = 18 (км/день).

Аналогично вычисляя средние скорости движения туристов по второму и третьему маршруту, получим соответственно

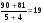(км/день) и 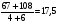(км/день).

Наибольшая средняя скорость (в км/день) движения туристов из пункта А в пункт В равна 19. Ответ: 19.

Задание В5.1 Решение линейных, квадратных, рациональных уравнений.

Теория

Линейные : Уравнение вида ax = b, где x – переменная, a и b некоторые числа, называется линейным уравнением с одной переменной.

Действия:

1. Раскрываем скобки (если есть)

2. Переносим слагаемые – меняем знак

3. Делим на коэффициент при переменной

4. Записываем ответ

Квадратное уравнение имеет вид ах²+bх+с=0,

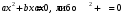Неполным квадратным уравнением называется уравнение вида

1. Уравнение вида 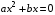решается разложением на множители – вынесением общего множителя за скобки и всегда имеет два корня, один из которых равен нулю.

2) Уравнение вида 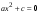решается только тогда, когда у коэффициентов а и с разные знаки. Оно решается разложением на множители по формуле разности квадратов.

Полные уравнения

;

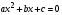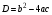
Если 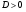, то 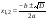- два корня.

Если 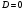, то 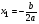- один корень.

Если 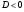, то корней нет.

Алгоритм решения:

1.Записать коэффициенты: а, b, с.

2.Вычислить дискриминант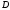

3.Применить формулу корней квадратного уравнения.

4.Записать ответ.

Уравнения, в которых левая и правая часть, являются дробно-рациональными выражениями, называются дробные рациональные уравнения.

Алгоритм решения дробных рациональных уравнений:

1) Найти общий знаменатель дробей, входящих в уравнение;

2) умножить обе части уравнения на общий знаменатель;

3) решить полученное целое уравнение;

4) исключить из его корней те, которые обращают в нуль общий знаменатель.

Полезно вспомнить ФСУ:

1.

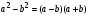
2.

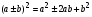
Практика

1.Найдите корень уравнения:

Решение:

Ответ: - 5.

2. Найдите корень уравнения: .

Решение:

Ответ: 13.

3.Решите уравнение:

Решение:

Ответ:-4

4. Найдите корень уравнения: Если уравнение имеет более одного корня, укажите меньший из них.

Решение: Ответ: 8.

5.Найдите корень уравнения:

Решение:

Ответ: 14

6. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Решение:

Ответ: 5.

7. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Решение:

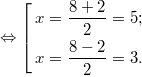ОДЗ:

Ответ: 5.

Задание В5.2 Решение иррациональных, показательных и логарифмических уравнений

Теория

Практика

Иррациональные уравнения

Иррациональными называются уравнения, в которых переменная содержится под знаком корня. При решении иррациональных уравнений, как правило, используют следующие методы: 
1) переход к равносильной системе (в этом случае проверка не нужна); 

Из двух систем выбирают ту, которая решается проще.  1.Если а < 0, уравнение не имеет корней. 2.Если , уравнение равносильно уравнению 2) метод возведения обеих частей уравнения в одну и ту же степень ( при решении простейших уравнений). 
3) метод введения новых переменных. Если вы не следите за равносильностью переходов, то проверка является обязательным элементом решения. О.Д.З. в иррациональных уравнениях не поможет Вам отсеять все посторонние корни. Обратите на это внимание!

Показательные уравнения

Уравнение, в котором переменная находиться в показатели степени, называется показательным. Для решения надо:

1) Привести левую и правую части уравнения к одному основанию.

2) Решить уравнение, приравняв показатели левой и правой частей уравнения.

Логарифмические уравнения

Логарифмическим называется уравнение вида

; где х>0, a>0.

Для решение логарифмических уравнений полезно повторить свойства логарифмов и приемы их вычисления ( из темы 7)

1. = 2; х - 3 = 4; х = 7 входит в ОДЗ. Ответ: 7.

2. ; <=>;;<=> <=> x = -1; Ответ: -1;

3.. Решить уравнение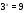

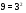
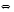
Решение. 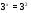.Основания одинаковы, степени равны, следовательно, показатели также равны. Ответ: 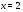. 4.Найти корень уравнения .

Решение: В данном случае замечаем, что . ; x-2=3 ;x=5. Ответ. 5

5.Найдите корень уравнения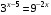

Решение. Используя свойства степеней,

; .

.

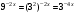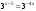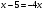
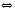
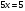
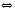
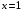Ответ: 1.

6.Решим уравнение:;

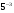; х – 7 =-3; х=4.

7. Найдите корень уравнения .

17+ х = 3

Х= 3 – 17

Х= - 14

8.Решим уравнение: ;

3+х = 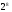; 3 + х = 256; х=253

9. Решим уравнение: ;

8 - 4х = 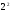; 8 – 4х = 4; -4х = -4; х =1

10. Решим уравнение: ; 4 - 4х = ;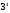

4 - 4х = 81; -4х =81-4; -4х=77; х= 77: (-4);

Х = - 19,25

Задание В5.3Тригонометрические уравнения

Теория

Практика

Простейшие тригонометрические ур-ия:

1. (), ;

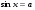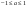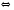
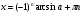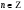2. (), ;

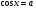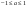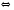
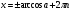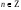3. , .

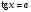
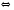
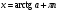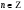Некоторые частные случаи:

1. , ;

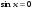
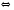
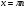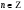2. , ;

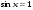
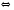
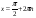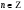3. , ;

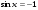
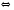
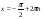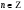4. , ;

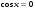
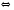
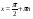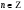5. , ;

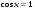
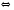
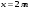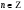6. , .

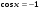
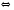
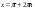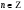Таблица значений тригон. -их функций:

α

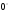
30

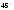
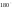
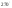
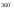
0

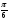
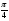
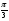
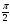
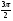
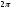
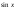
0

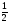
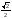
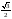
1

0

-1

0

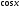
1

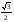
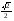
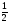
0

-1

0

1

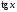
0

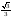
1

-

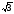
0

-

0

-

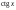
1

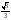
0

-

0

-

1.Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

Решение:

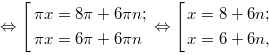
где — целое.

Наибольшим отрицательным корнем будет -4 .

Ответ: −4.

2. Решите уравнение . В ответе напишите наибольший отрицательный корень.

Решение:

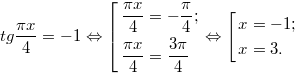
Ответ: −1.

3. Решите уравнение . В ответе напишите наименьший положительный корень.

Решение:

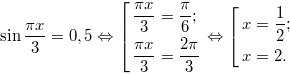
Ответ: 0,5.

В итоге наблюдается:

1. Высокая степень самостоятельности и активности учащихся.

2. Усвоение материала на конструктивном уровне с ориентацией учеников на уровень творчества.

3. Перенос акцента в обучении с преподавания на учение.

4. Метод работы с мини-справочниками относится к здоровьесберегающему, поэтому за ним большое будущее, ни только на уроках, но и во внеурочное время, на элективных курсах - в любой практической деятельности по подготовке к экзаменам.

5. Формируются такие качества, как сила воли, ответственность, добросовестность, умение доводить начатое дело до конца.

6. Ученики становятся уверенными, что и они пройдут «порог ЕГЭ» и смогут, используя применение новых мини-справочников, продолжить повторение и набрать баллы по В6-В14.

Список используемой литературы и материалов:

1. Открытый банк заданий ЕГЭ по математике

2. Селевко Г.К. Современные образовательные технологии: Учебное пособие. - М.: Народное образование, 1998. - 256 с

3. Сайт: http://reshuege.ru/

4. Сайт: http://www.matematika-ege.ru/

5. Сайт: http://www.mathege.ru:8080/or/ege/Main.html?view=Pos

6. Сайт: www1.ege.edu.ru.

7. Шаталов. В.Ф. Точка опоры; Изд-во: М.: Педагогика, 1987г.