Треугольник Паскаля 8 Класс

Региональный этап Российской научной конференции

школьников «Открытие»

Секция математика

Треугольник Паскаля

Исследовательская работа

Выполнена ученицей

8а класса Муниципального бюджетного общеобразовательного учреждения « Засосенская средняя общеобразовательная школа

имени Героя Советского Союза Н.Л. Яценко»

Махнёвой Екатериной Сергеевной

Научный руководитель -

учитель математики

Муниципального бюджетного общеобразовательного учреждения « Засосенская средняя общеобразовательная школа

имени Героя Советского Союза Н.Л. Яценко»

Михайличенко Зинаида Ивановна

Засосна, 2012

Одна из глав курса геометрии называется «Треугольники». Меня очень заинтересовала данная тема. Я всегда хотела узнать много нового о треугольниках. Ведь мир треугольников очень загадочен и интересен. Я хочу узнать как можно больше о происхождении треугольников, об их значении в нашей жизни.

Треугольник - первая геометрическая фигура, встречающаяся в древних орнаментах. Изучая литературу, я узнала, что в Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.

В герметической идеографии треугольник с устремленной к верху вершиной, символизирует огонь и отвечает идее вознесения, духовности, красному цвету. Треугольник с горизонтальной чертой считается пассивным и означает воздух, умеренный огонь, соответствующий синему цвету. Перевернутый треугольник означает чашу, готовую принять воду; мудрость, порождающую главную идею; зеленый цвет. Треугольник воздуха с горизонтальной чертой символизирует Землю, неподвижную стоячую воду и соответствует черному цвету. Ацтеки использовали изображение треугольника с вершиной наверху, соединенного с перевернутым треугольником, в качестве символа временного цикла. Треугольник в сочетании с крестом образует алхимический знак Серы.

Равносторонний треугольник, символизирующий, по древнееврейской традиции, совершенство, у христиан означает Троицу - Отца, Сына и Святого Духа.

Существует множество видов треугольников, но больше всего меня заинтересовал треугольник Паскаля.

Актуальность проекта

Данный проект предназначен для выявления того, насколько широко треугольники используются в практической жизни.

Новизна проекта

Новизна моего исследования состоит в том, что я попыталась показать связь треугольников с жизнью.

Практическая значимость проекта

Данный проект может быть использован как дополнительный материал к урокам геометрии, для внеклассной работы по математике.

Цель проекта

- ознакомиться с треугольником Паскаля как разновидностью треугольников;

- рассмотреть применение треугольника Паскаля в различных сферах;

- подготовить презентацию, содержащую полученные результаты и продемонстрировать её другим учащимся на уроке.

Гипотеза

Если числа треугольника Паскаля обладают особыми свойствами, то его можно считать волшебным.

Задачи

- изучить литературу по теме «Треугольник Паскаля»;

- выявить свойства чисел, входящих в состав треугольника Паскаля;

- определить применение свойств чисел треугольника Паскаля;

- сформулировать вывод и итоги исследования;

- создание иллюстративного компьютерного материала по треугольникам;

- выступить с презентацией своей творческой работы.

Объект исследования: треугольник как геометрическая фигура

Предмет исследования: свойства треугольника Паскаля

Методы исследования:

- аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;

- поиск информации в интернет - ресурсах.

Направления работы:

- выбор проблемы, источников литературы, составление плана;

- работа с литературой и другими источниками;

- обработка полученных данных;

- анализ результатов, формулирование вывода;

- мультимедийная подготовка.

Основные этапы проекта: подготовительный; деятельностный;

ход исследования; рефлексивный; аналитический; презентационный.

Теоретическая часть работы

Блез Паскаль – французский математик

Блез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик, литератор и философ.

Паскаль был первоклассным математиком. Он помог создать два крупных новых направления математических исследований. В возрасте шестнадцати лет написал замечательный трактат о предмете проективной геометрии и в 1654 году переписывался с Пьером де Ферма по теории вероятностей, что впоследствии оказало принципиальное влияние на развитие современной экономики.

Треугольник Паскаля как разновидность треугольника

Изучая разновидности треугольников, я выяснила, что треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля. В действительности, треугольник Паскаля был известен задолго до 1653 года - даты выхода "Трактата об арифметическом треугольнике". Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.
Ещё я узнала из книги "Математические новеллы" (М., Мир, 1974) Мартина Гарднера, что "Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике".

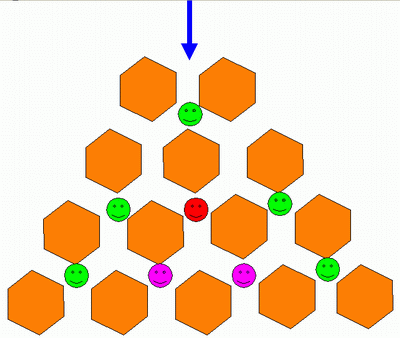
Я рассмотрела схему построения треугольника, предложенную Гуго Штейнгаузом в его классическом «Математическом калейдоскопе»: предположим, что вы входите в город как показано на схеме синей стрелкой, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо. Узлы, в которые можно попасть только единственным образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, показана красным смайликом, а тремя, соответственно - розовыми. Это один из вариантов построения треугольника.
( Приложение 1)

Изучая специальную литературу, я узнала, что еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух расположенных над ним чисел. Все элементарно, но сколько в этом таится чудес. Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Треугольник можно продолжать неограниченно. Он обладает симметрией относительно вертикальной оси, проходящей через его вершину. Вдоль диагоналей (насколько у треугольника могут быть диагонали, но не будем придираться, такая терминология встречается в публикациях), параллельных сторонам треугольника (на рисунке отмечены зелеными линиями) выстроены треугольные числа и их обобщения на случай пространств всех размерностей. Треугольные числа в самом обычном и привычном нам виде показывают, сколько касающихся кружков можно расположить в виде треугольника - как классический пример начальная расстановка шаров в бильярде. К одной монетке можно прислонить еще две - итого три - к двум можно приладить еще три - итого шесть.
Продолжая наращивать ряды с сохранением формы треугольника получим ряд 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66..., что и показывает вторая зеленая линия. Этот замечательный ряд, каждый член которого равен сумме натурального ряда чисел (55=1+2+3+4+5+6+7+8+9+10), содержит также множество знакомцев, хорошо известных любителям математики: 6 и 28 - совершенные числа, 36 - квадратное число, 8 и 21 - числа Фибоначчи.
Следующая зеленая линия покажет нам тетраэдральные числа - один шар мы можем положить на три - итого четыре, под три подложим шесть - итого десять, и так далее.
А следующая зеленая линия (1, 5, 15, 35,...) продемонстрирует попытку выкладывания гипертетраэдра в четырехмерном пространстве - один шар касается четырех, а те, в свою очередь, десяти... В нашем мире такое невозможно, только в четырехмерном, виртуальном. И тем более пятимерный тетраэдр, о котором свидетельствует следующая зеленая линия, он может существовать только в рассуждениях топологов.
А о чем же говорит нам самая верхняя зеленая линия, на которой расположились числа натурального ряда? Это тоже треугольные числа, но одномерные, показывающие, сколько шаров можно выложить вдоль линии - сколько есть, столько и выложите. Если уж идти до конца, то самый верхний ряд из единиц - это тоже треугольные числа в нульмерном пространстве - сколько бы шаров мы не взяли - больше одного расположить не сможем, ибо просто негде - нет ни длины, ни ширины, ни высоты.
Даже беглого взгляда, брошенного на треугольник Паскаля, достаточно, чтобы отметить следующие любопытные факты: 10 ядер можно сложить и в виде тетраэдра и в виде плоского треугольника. А 56 гиперядер, образующих тетраэдр в пятимерном пространстве, можно уложить в обычный привычный трехмерный тетраэдр, однако, если бы мы попытались выложить из 56 ядер треугольник, то одно ядро осталось бы лишним. ( Приложение 2)

Треугольник Паскаля имеет применение в теории вероятностей и обладает замечательными свойствами.

Свойства треугольника Паскаля и их применение в решении задач

Изучая свойства треугольника Паскаля, я рассмотрела одно из свойств биномиальных коэффициентов:

Данное равенство показывает, что биномиальные коэффициенты можно последовательно выписывать в виде треугольной таблицы, которая называется треугольником Паскаля. В n-ой строке треугольника Паскаля стоят коэффициенты разложения , причем каждый коэффициент, кроме крайних двух, которые равны 1, равен сумме соответствующих коэффициентов из предыдущей строки.

Я узнала, что треугольник Паскаля - это бесконечная числовая таблица "треугольной формы", в которой по боковым сторонам стоят единицы и всякое число, кроме этих боковых единиц, получается как сумма двух предшествующих чисел. В такой форме треугольник Паскаля появился в сочинении Паскаля "Трактат об арифметическом треугольнике", изданном в 1665 г. уже после смерти автора. Более точно, в указанном сочинении была опубликована следующая таблица, в которой каждое число А равно сумме предшествующего числа в том же , что и А, горизонтальном ряду, и предшествующего числа в том же, что и А, вертикальном ряду:

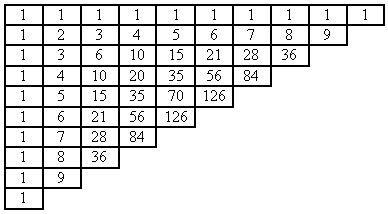
Паскаль подробно исследовал свойства и применения своего "треугольника". Приведу для примера лишь 3 свойства "треугольника", найденные самим Паскалем; при этом буду исходить из того расположения "треугольника" на плоскости, какое было указанно Паскалем, и говорить о горизонтальных и вертикальных рядах. Свойство 1: Каждое число А в таблице равно сумме чисел предшествующего горизонтального ряда, начиная с самого левого вплоть до стоящего непосредственно над числом А (в котором клетки, содержащие слагаемые, дающие в сумме А, заштрихованы).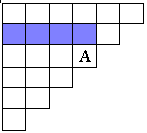

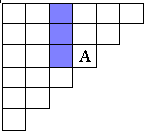
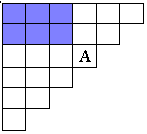
рис.1 рис. 2 рис. 3

Свойство 2: Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А. Рис. 2. Свойство 3: Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми вертикальными и горизонтальными рядами, на пересечении которых стоит число А (сами эти ряды в рассматриваемый прямоугольник не включаются). Рис. 3.

Таким образом, наш треугольник отличается от "треугольника" рассматриваемого самим Паскалем, поворотом на 45 градусов.

Я пришла к выводу, что рассмотренные свойства треугольника Паскаля подтверждают слова Мартина Гарднера о том, что треугольник Паскаля одна из наиболее изящных схем во всей математике.

Актуальность исследования обусловлена ежегодным усложнением заданий ГИА и ЕГЭ, что требует углубленных знаний не только в алгебре, но и в геометрии.

Практическая часть работы

1. Решите следующие задачи

В своей практической работе я подобрала ряд задач по теме «Треугольник Паскаля»

1. В числовом треугольнике

как известно, каждое число равно сумме чисел, расположенных в предыдущей строке над этим числом и над его соседями справа и слева. Доказать, что в каждой строке, начиная с третьей, найдется четное число. 2. Первая строка числового треугольника

состоит из чисел 0,1,...,1958. Элементы каждой следующей строки являются суммами элементов предыдущей строки, стоящих слева и справа от данного числа. Доказать, что элемент последней строки треугольника делится на 1958. 3. Существует ли в треугольнике Паскаля число 2010? 4. Найти сумму биномиальных коэффициентов десятой строки треугольника Паскаля. 5. Выпишите разложение (2a-b). 6.Найдите коэффициент разложения (a+3b) для слагаемого, содержащего буквенную часть, равную аb. 7. В пятнадцатой строке прочередуйте знаки “+” и ”-“. Чему равно значение полученного выражения? 8. Какое число, большее 1, содержится в треугольнике Паскаля более трёх раз? четырех раз? 9. Сколько нечетных чисел в 8-ой строке, в 16-ой, 32-ой? 10. Во сколько раз сумма чисел в 12-ой строке треугольника больше суммы чисел в 7-ой строке? 11. Сколькими способами шахматный король может пройти из левого нижнего угла в правый верхний? 12. Сколькими способами можно решить правильно 4 уравнения из 9?

2. Геометрия вокруг нас Исследовала практическую значимость треугольников в окружающей нас жизни. (Приложение 5)

Заключение

Работа по выбранной теме осуществлялась в полном соответствии с планом исследования, а именно: были определены объектная область, объект и предмет исследования, поставлены цели и задачи, а также определены ожидаемые результаты. Были указаны используемые методы исследования, определена проблема, обоснована актуальность.

В данной работе была дана общая характеристика треугольника как геометрической фигуры, был детально рассмотрен треугольник Паскаля, его свойства.

Я пришла к выводу, что одной из наиболее известных и изящных численных схем во всей математике является треугольник Паскаля. Треугольник Паскаля - понятие значительно шире, чем мне представлялось. Он обладает не только удивительными свойствами, но и применялся в архитектуре средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами.

Практическая значимость данной работы заключается в следующем:

я, изучив много литературы по данному вопросу, получила дополнительные знания в области математики, укрепила свой интерес к этой науке.

Работа по данной теме оказалась интересной и полезной.

Список использованных источников и литературы

1. Абачиев С. К. Радужная фрактальность треугольника Паскаля

2. Мартин Гарднер. Глава 17. Неисчерпаемое очарование треугольника Паскаля // Математические новеллы. — М.: Мир, 1974. — 456 с. 3. Треугольник Паскаля. В. А. Успенский. - 2 - е изд. – М.: Наука, 1979. – 48с.

4. Удивительный треугольник великого француза // Hard'n'Soft № 10 2003

5. Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант. — 1970. — № 6. — С. 17-25.

6. Энциклопедия для детей. Т 11. Математика / Глав. ред. М. Аксенова; метод. и отв. ред. В. Володин. – М.: Аванта+,2004. – 688с.

7. http://ru.wikipedia.org/wiki/

8. Weisstein, Eric W. Pascal's Triangle (англ.) на сайте Wolfram MathWorld.