Государственное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №1

с.Летняя Ставка

Учитель: Муратова Галия Мовлитбердыевна

Предмет: Математика

Класс: 6 а

Тема урока: «Координатная плоскость»

Тип урока: Урок закрепление учебного материала

Цель: Формирование понятия «координатная плоскость», отработка навыков нахождения точки по ее координатам и определения координат точки, отмеченной на координатной плоскости.

Задачи:

• Обучающие:

Сформировать понятие прямоугольной системой координат на плоскости, сформировать представление о взаимно однозначном соответствии между точкой на координатной плоскости и ее координатами; отработать навыки нахождения точки по ее координатам и определения координат точки, отмеченной на координатной плоскости; расширить кругозор учащихся в историческом аспекте;

• Развивающие:

активизировать познавательную деятельность учащихся; развивать логическое мышление, умения анализировать, сравнивать, обобщать, выделять главное, делать выводы; развивать быстроту реакции, развивать память; развивать творческие способности учащихся; развивать умения учебного труда (умения работать в нужном темпе – писать, конспектировать, чертить); развивать умения и навыки применять математические знания к решению практических задач;

• Воспитательные:

воспитывать у учащихся интерес к математике, к познанию; воспитывать аккуратность и культуру графических построений; воспитывать самостоятельность, волю и настойчивость, уверенность в своих силах, стремление к достижению результата.

Технологии:

• Информационно-коммуникационные технологии;

• Технология развития «критического мышления»;

• Исследование в обучении;

• Игровые технологии: обучающие игры;

• Технология решения изобретательских задач (ТРИЗ).

Оборудование:

Компьютер, мультимедийный проектор, экран, презентация в программе PowerPoint, индивидуальный раздаточный материал для учащихся (карточки с координатами точек, образующих рисунок).

Ход урока:

1. Организационный момент.

Добрый день ребята! А хочу я ребята начать урок с притчи.

Лавка возможностей

«Однажды человеку приснился сон, будто он идет по городу и заходит в торговую лавку. Он долго ходит среди разнообразных экзотических заморских овощей и фруктов. Там есть весьма странные и необычные плоды и ягоды, даже и близко не похожие на те, что он ранее видел.
Одни привлекают его своими невероятными красками, другие манят предвкушением райского аромата, третьи — изысканными звуками, доносящимися из сердцевины фрукта. И, конечно же, каждый из людей выбирает то, что ему по душе, и часто оказывается, что именно это ему и необходимо.

Но как только человек брал в руки какой-нибудь фрукт, тот исчезал, оставляя на ладони крохотное семечко. Немало удивленный, он решил схитрить и подошел к хозяину лавки: «Дайте мне, пожалуйста, вон тот фрукт», — сказал он и показал на полку. Однако хозяин ответил ему: «Мы не торгуем плодами, мы торгуем семенами…».

Каждый сделает выводы сам, а к притче мы с Вами вернемся немного позже.

Ребята, я предлагаю Вам урок-творчества!

2. Введение в тему.

От простого к сложному.

Скажите, когда вы дома не убираете за собой, что говорит вам мама?

А как расположены молекулы газа?

Иначе говоря хаотично.

-Хаос понимают как беспорядок, неразбериху, смешение. Понятие возникло от названия в древнегреческой мифологии изначального состояния мира, из которой возникли первые божества. Лишь в раннехристианские времена этому слову стали приписывать значение беспорядка.

-А почему вы сели именно так?

-А расположение молекул твердого тела?

-Порядок в широком смысле слова — гармоничное, ожидаемое, предсказуемое состояние или расположение чего-либо.

-Расположение песка в пустыне беспорядочно, то есть хаотично. А если песчинки привести в порядок, то могут получиться такие замечательные картины. Как это делал Эшер в своих картинах, изображал порядок.

Существование городов на земной поверхности было в хаотичном порядке, пока немецкий географ Мартин Бехайм в 1492 году изобрел модель земли – глобус. Идея задавать положение точки на плоскости зародилась в древности – прежде всего у астрономов. Во II в. древнегреческий астроном  Клавдий Птолемей пользовался широтой и долготой в качестве координат.

Координата – это положение точки на плоскости или в пространстве. Термин «координаты» произошел от латинского слова – «упорядоченный»

А сейчас давайте узнаем с чьим именем связано прямоугольная система координат?

Математический кроссворд

1

2

3

4

5

6

По горизонтали:

1. Вспомните компоненты действия деления. Как называется то число, которое делим?

2. Значение переменной, которое обращает уравнение в верное числовое равенство.

3. Параллелепипед, в котором все ребра равны.

4. Вспомните компоненты действия сложения. Как называется число, которое складывают?

5. Равенство, содержащее неизвестное число, обозначенное буквой.

6. Результат действия деления.

Ответы:

1

Д

Е

Л

И

М

О

Е

2

К

О

Р

Е

Н

Ь

3

К

У

Б

4

С

Л

А

Г

А

Е

М

О

Е

5

У

Р

А

В

Н

Е

Н

И

Е

6

Ч

А

С

Т

Н

О

Е

Найдите получившуюся по вертикали фамилию человека, о котором и пойдет речь на сегодняшнем уроке.

Ответ: Декарт

Рене́ Дека́рт (1596 — 1650) — французский математик, философ, физик и физиолог.

Именно он придумал в 1637 году систему координат, которая используется во всем мире и известна каждому школьнику. Ее называют также - Декартова система координат.

Координатный метод описания геометрических объектов положил начало особой ветви математики - аналитической геометрии.

3. Работа у доски

В координатной плоскости точки расположены хаотично, то есть беспорядочно. Упорядочим расположение точек на оси ОХ и ОУ. Что получилось? Получился определенный порядок.

«Кто испытал наслаждение творчеством, для того уже другие наслаждения не существуют» А.П. Чехов

- Давайте вместе с Вами испытаем наслаждение творчеством. Упорядочим точки в координатной плоскости так, чтобы получился фигурки рыбы. А чтобы упорядочить актуализированные ранее мысли, послушайте классическую музыку

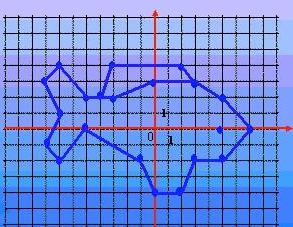
(0;7)

(2;5)

(2;4)

(4;5)

(3;0)

(4;1)

(4;0)

(7;2)

(6;-1)

(7;-1)

(3;-4)

(3;-5)

(0;-3)

(1;-7)

(0;-7)

А теперь получим осенний листок. Давайте подойдем творчески: Чего не хватает? Что для этого надо сделать?(отразить относительно оси оу)

4.Работа в группах

История звёздной карты началась в глубокой древности. Мы не знаем, кто и когда первым поместил самые яркие звёзды в пространство воображаемых фигур. Но даже далекие от астрономии люди умеют находить на небе Большую и Малую Медведицы. Благодаря своей близости к северному полюсу мира, в средних широтах нашей страны Медведицы являются незаходящим созвездием, поэтому их можно отыскать на небе в любое время от заката до рассвета в течение всего года. Однако все это содержание неба, а форма? После выполнение данного задания эта неуловимая красота, будет нам доступна.

1 Группа " МАЛАЯ МЕДВЕДИЦА"

А(6,1) - В(3,3) - С(0,4) - D(-3,1) - Е(-6,-1) - Р(-8,1) - G(-5,3) –D

2. Группа "БОЛЬШАЯ МЕДВЕДИЦА"

А(-15,0) - В(-10,2) - С(-1,5) - D(-3,0) - Е(6,1) - F(5,-3) - G(-l,-3) – D

2. Группа " ПЕРСЕЙ "

А(-5,-3) - В(-2,-2) - С(0,-1) - D(2,-2) - E(4,-l) - F(5,0) - G(6,2)

H(l,3) - K(1,0) – С

2. Группа "КАССИОПЕЯ "

А(-3,2) - В(-1,0) - С( 1,1) - D(3,-2) - Е(5,0)

довольно яркое созвездие в виде латинской буквы W (см. рисунок). Это и есть Кассиопея.

Ребята вы знаете, что означает пара таких чисел как 01,02,03,911, 0;5-3;4

Давайте узнаем? У Вас получилась четверть окружности. Симметрично отобразим точки и соединим. Получим окружность. А это простое правило вы можете использовать в случаи отсутствия транспортира.

VI. Рефлексия

-У каждого из Вас на столе имеются по три листика: желтый, зеленый и красный. Ответьте, пожалуйста, на следующие вопросы, используя листочки. Красный – нет, желтый - сомневаюсь, зеленый – да.

1. Вам интересна данная тема?

2. Примете ли Вы идею использования хаоса и порядка. Каким образом?

3. Получили ли Вы семя знаний о декартовой система координат, которое хотелось бы растить?

Сегодня на уроке при помощи декартовой системы координат мы рассмотрели

Геогафию

Астрономию

Математику

Физику

Ботанику (песчинки - почва)

Бытовую сферу

VII. Домашнее задание (дифференцированное)

Построить рисунок по координатам. (Учитель раздает карточки с координатами точек, найдя и последовательно соединив которые, учащиеся смогут дома построить рисунок на координатной плоскости.)

(рисунок - слон):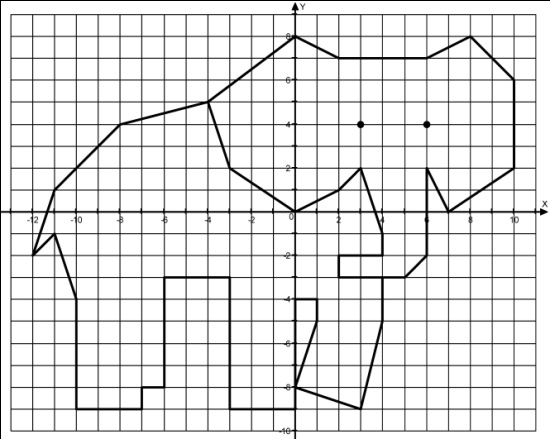

(0;1), (4;1), (6;2), (8;0), (8;-4), (5;-6), (4;-4), (4;-8), (3;-9), (2;-9), (0;-9), (0;-8), (2;-8), (3;-7), (1;-5),

(0;-5), (-1;-4), (-2;-6), (-5;-4), (-6;-1), (-2;2), (-10;-2), (-13;-4), (-14;-7), (-16;-9), (-13;-7), (-12;-10),

(-13;-14), (-10;-14), (-9;-13), (-10;-9), (-5;-9),

(-5;-15), (-2;-15), (-2;-10), (-1;-10), (-1;-11), (-2;-13), (0;-15), (2;-11). Глаза: (0;-2), (4;-2).

И творческое домашнее задание на неделю: Придумать самостоятельно и нарисовать на координатной плоскости животное, состоящее из ломаных, а затем "зашифровать" его с помощью координат точек. Лучшие работы будут вывешены в классе.