Урок – семинар по теме «Показательная функция»
Автор: учитель математики МОУ «Средняя общеобразовательная школа №41»
г.о. Саранск Тарабина Галина Михайловна
Урок – семинар по теме: « Показательная функция» (слайд 1)
Цель урока: Повторить свойства показательной функции, способы решения уравнений, неравенств, систем уравнений.
Сегодня на уроке-семинаре мы подведем итоги изучения темы «Показательная функция».
Наш класс разбит на три группы, т.е. работа у нас сегодня групповая, каждый из вас получит оценку, которую заработаете группой. На нашем семинаре вам необходимо будет разгадать кроссворд, ответить на теоретические вопросы, вы поучаствуете в ярмарке задач, выполните индивидуальную работу. Каждая группа представит свою творческую работу, которая поможет вам глубже познать данную тему.
1этап 1.команда – разгадывает кроссворд,
2.команда играет в домино,
3. команда отвечает на вопросы.
Кроссворд «И в шутку и всерьез». (слайд 2)

По горизонтали:
6.Есть у любого слова, у растения и может быть у уравнения.
По вертикали:
1.Название функции, любой из графиков, которой обязательно пройдет через точку (0;1).
2.Исчезающая разновидность учеников.
5.Проверка учеников на выживание.
3.Ученый математик, механик и астроном. Его высказывание о показательной функции напечатано в учебнике перед первым параграфом.
4.Другое название независимой переменной в функции.
(Ответ. 1. Показательная. 2. Отличник. 3. Эйлер. 4. Аргумент. 5. Контрольная. 6. Корень.)
Игра Домино. (слайд6) Решите показательные уравнения и неравенства ( ученикам раздаются карточки с заданиями и ответами к ним)
3х ≥ 27
2х = 4
![]() ≤ 25
≤ 25
16х = 4
х ≥ 3, х = 2
х ≥ - 2
х = ![]()
![]() = 36
= 36
7 х+1 = 49
99х = 1
х = - 2
х = 1 х = 0
Ответ: (слайд 6)
3х ≥ 27
2х = 4
х = 2
![]() ≤ 25
≤ 25
х ≥ - 2
16х = 4
х ≥ 3
х = ![]()
![]() = 36
= 36
х = - 2
х = 1
7 х+1 = 49
х = 0
99х = 1
Вопросы к 1 команде: (слайд 3)
1) 9,80 .
2) Область определения функции у = 4х.
3) Метод решения уравнения 3х+1 – 3х-2 = 26.
4) Решить неравенство 3х < 34.
5) 3х = 1, при х =
6) Возрастает или убывает функция у =![]()
7) Что такое функция?
8) Функция у = ах, при а >1 …
9) Множество значений показательной функции.
Ответ. 1.1; 2. х- любое. 3. вынесение за скобки. 4. х меньше 4;. 5.х=0;. 6.убывает 8. Функция у = ах, при а >1, возрастает; 9. Множество значений показательной функции-множество положительных чисел
Вопросы к 2 команде: (слайд 4)
1) 7,80 .
2) Область определения функции у = 0,3х .
3) Метод решения уравнения 9х – 3х + 45 = 0.
4) Решить неравенство ﴾![]() ﴿х > ﴾
﴿х > ﴾![]() ﴿2 .
﴿2 .
5) 4х = 1, при х =
6) Возрастает или убывает функция у=4х .
7) Функция у = ах, при 0 <а <1 …
8) Область определения показательной функции.
9) Какая функция называется убывающей?
Ответ. 1.1; 2. х- любое. 3. свести к квадратному уравнению 4. х меньше 2;. 5.х=0;. 6.возрастает 7 Функция у = ах, при 0 <а <1 убывает.; 8. Область определения показательной функции- х- любое
Вопросы к 3 команде: (слайд 5)
1) 6,30
2) Область определения функции у = 2,5х.
3) Метод решения уравнения 3х-1 + 3х = 4.
4) Решить неравенство 5х > 58 .
5) 5х =1, при х =
6) Возрастает или убывает функция у = 4,8х
7) Как называются переменные в записи функции?
8) Функция у = ах, при а>1 ..
9) Какая функция называется возрастающей?
Ответ. 1.1; 2. х- любое. 3. вынесение за скобки. 4. х больше 8;. 5.х=0;. 6.возрастает 8. Функция у = ах, при а >1, возрастает;
2. Этап. Ярмарка задач.
1. Решите уравнение.![]()
81х = 3.
2. Решите неравенство.
![]()
![]() 1.
1.
3.Решите систему уравнений.
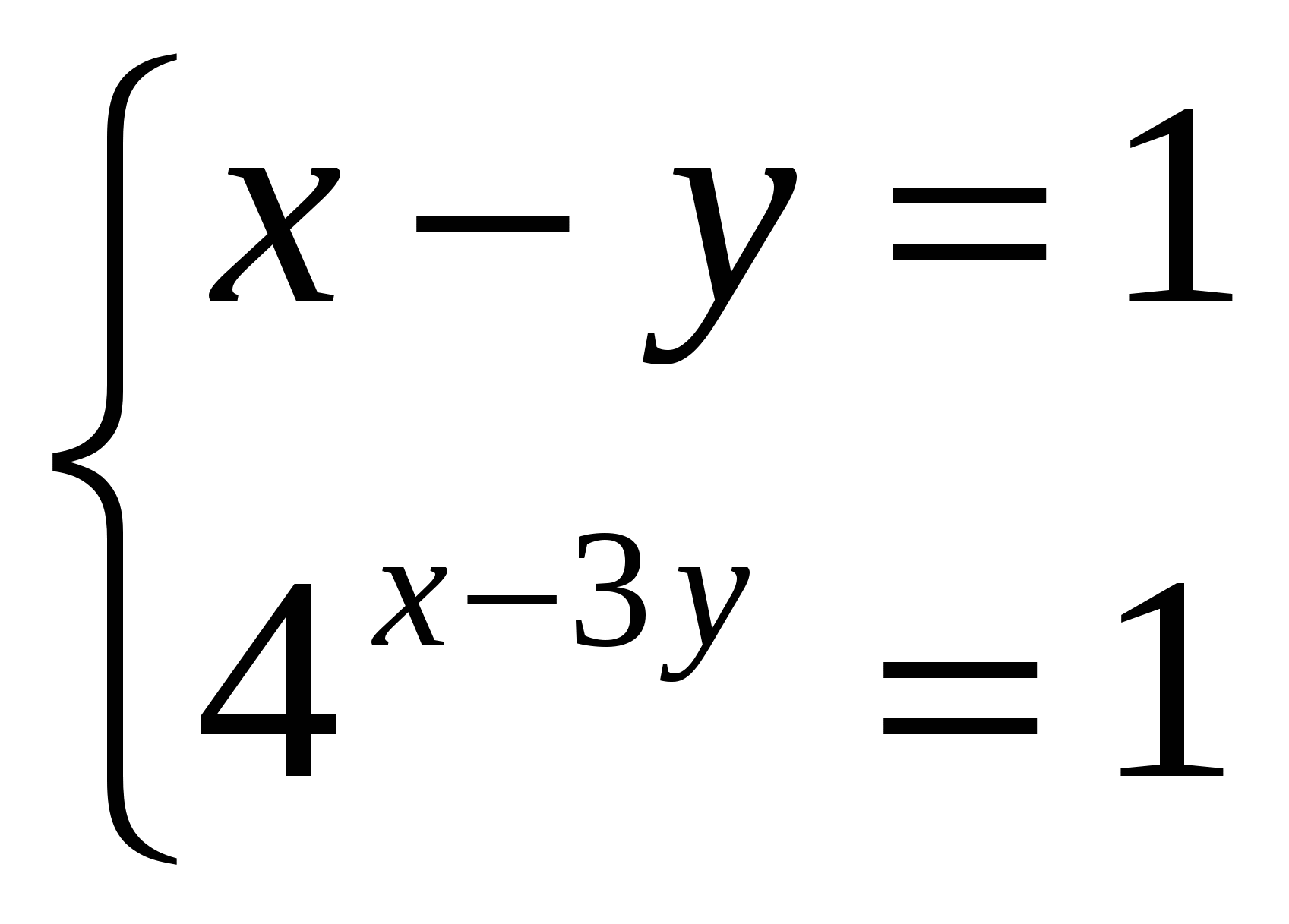
4. Решите уравнение.
![]()
5. Решите неравенство.
3х+2 + 3х-1 ≤ 28.
6. Решите уравнение
.72х+1 - ![]() 7х +1 = 0.
7х +1 = 0.
7. Решите неравенство.
9х + 3х – 12 ![]() 0.
0.
8. Решите систему.
![]()
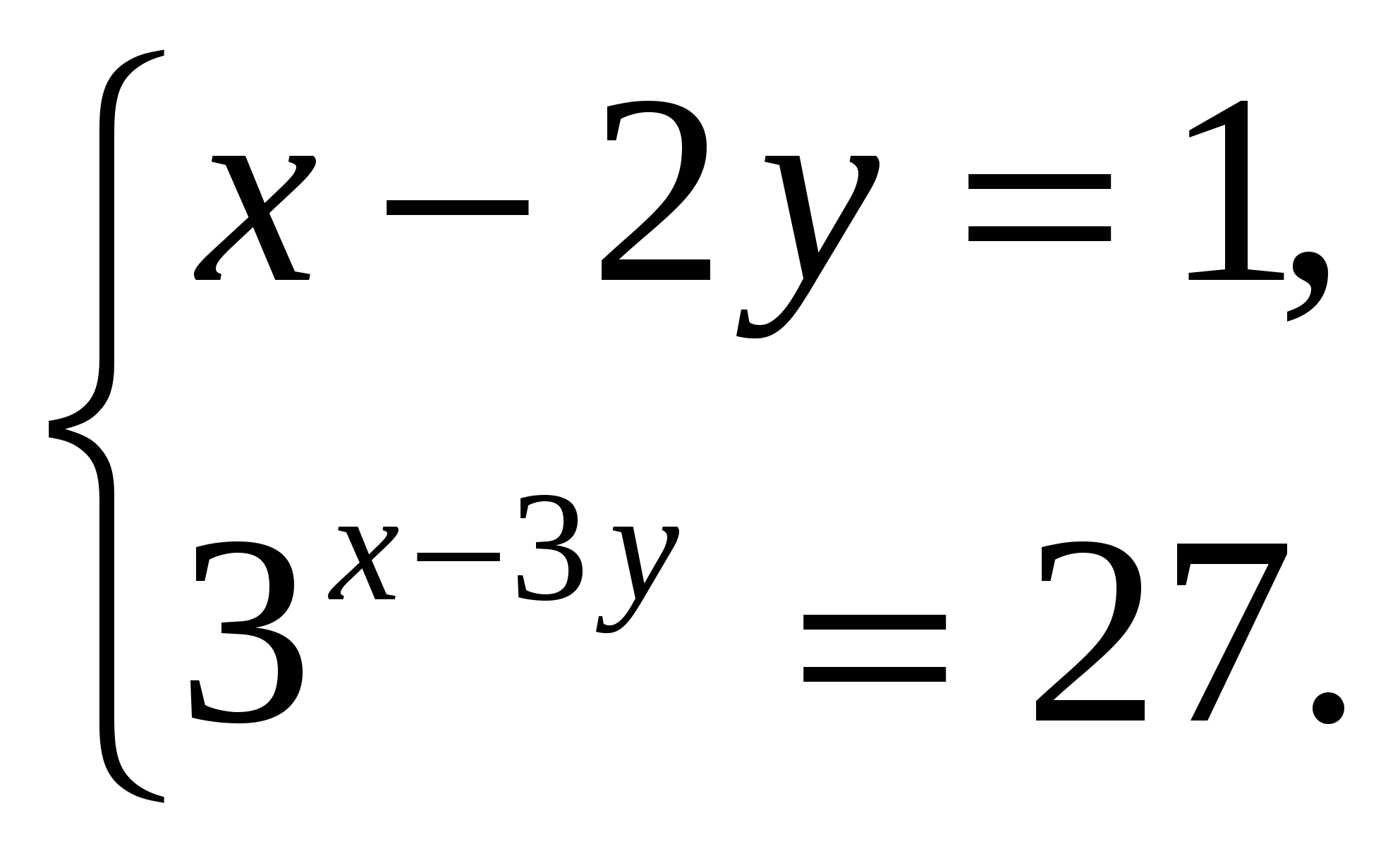
О![]()
![]()
![]() тветы: (слайд 7)1. 2. 3.
тветы: (слайд 7)1. 2. 3.  4.
4.![]() 5.
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
3. Этап .Готовясь к семинару, каждая группа подготовила интересное задание по нашей теме.
Слово первой группе.
Задача 1. При каких значениях параметра p уравнение 4x – (5p – 3)2x + 4p2 – 3p = 0 (1) имеет единственное решение?
Решение. Введем замену 2x = t, t > 0, тогда уравнение (1) примет вид t2 – (5p – 3)t + 4p2 – 3p = 0. (2)
Дискриминант уравнения (2) D = (5p – 3)2 – 4(4p2 – 3p) = 9(p – 1)2.
Уравнение (1) имеет единственное решение, если уравнение (2) имеет один положительный корень. Это возможно в следующих случаях.
1. Если D = 0, то есть p = 1, тогда уравнение (2) примет вид t2 – 2t + 1 = 0, отсюда t = 1, следовательно, уравнение (1) имеет единственное решение x = 0.
2. Если p![]() 1, то 9(p – 1)2 > 0, тогда уравнение (2) имеет два различных корня t1 = p, t2 = 4p – 3. Условию задачи удовлетворяет совокупность систем
1, то 9(p – 1)2 > 0, тогда уравнение (2) имеет два различных корня t1 = p, t2 = 4p – 3. Условию задачи удовлетворяет совокупность систем
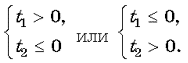 Подставляя t1 и t2 в системы, имеем
Подставляя t1 и t2 в системы, имеем
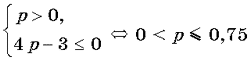 или
или 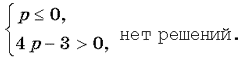
Ответ: p = 1, 0 < p 0,75.
Слово второй группе.
Задача 2. Решите неравенство.
![]() ≤ 4.
≤ 4.
Решение.
![]()
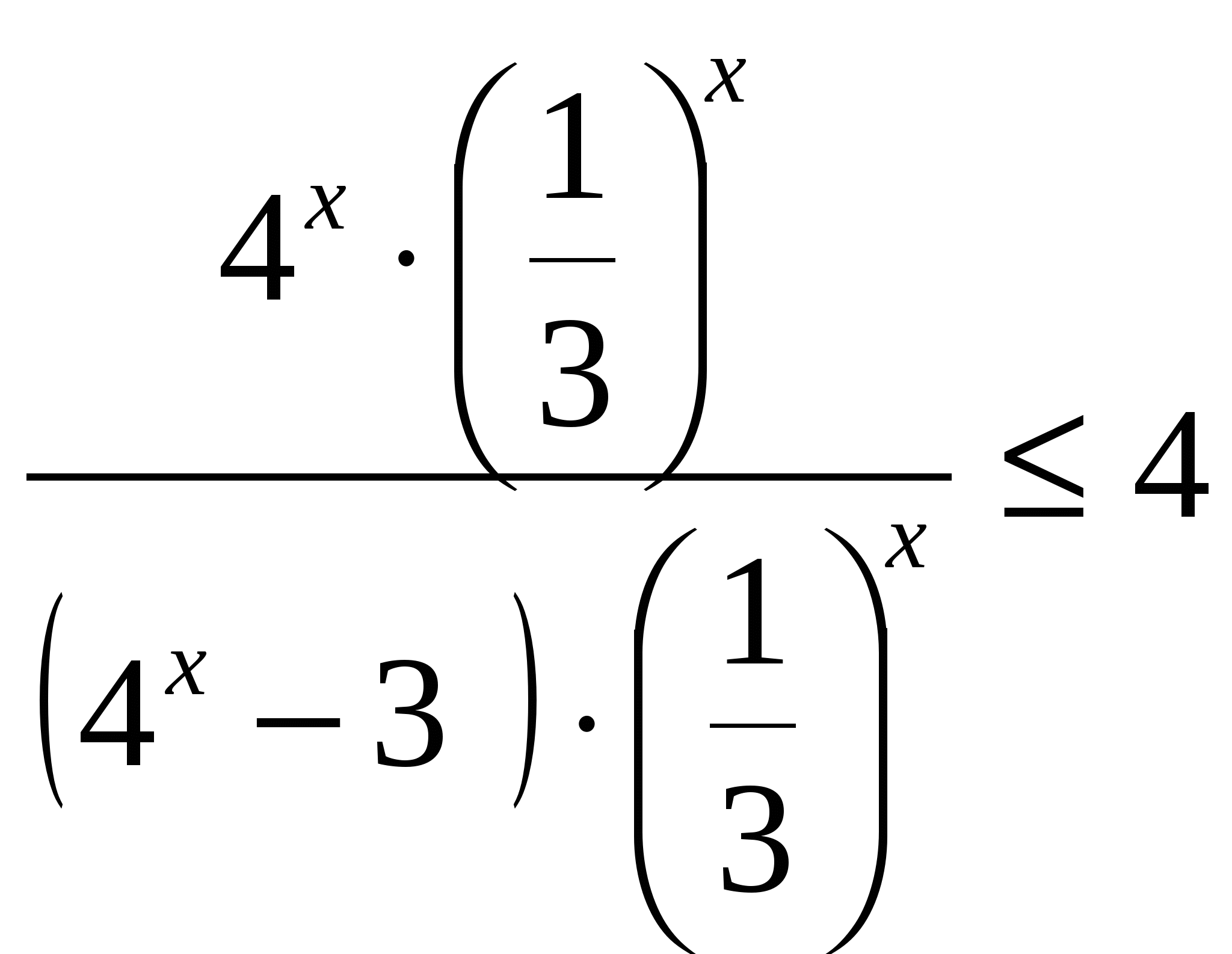 ,
, 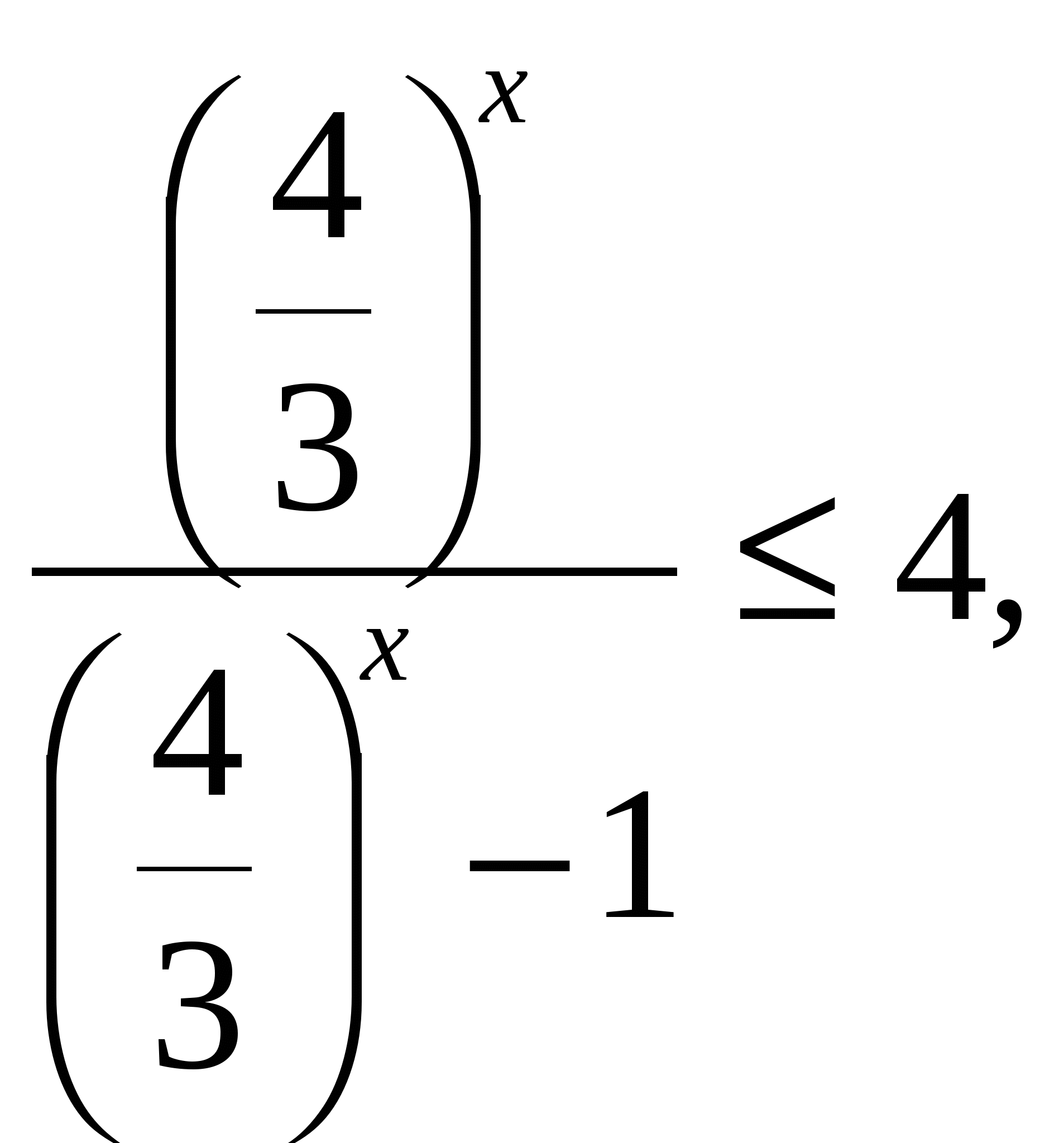
Пусть ![]()
![]()
![]() , тогда
, тогда ![]()
![]() ,
,![]() ,
,
![]() Т.к
Т.к ![]() то
то
![]()
Возвращаясь к переменной х, получим
1) ![]()
![]()
2) ![]() ,
, ![]()
Ответ: х≤0, х≥1.
Слово третьей группе.
Задача 3. Решите уравнение.
8х + 18х = 2 . 27х .
![]()
![]()
![]()
![]() ,
,
Пусть ![]() , тогда
, тогда
![]()
![]()
![]()
![]()
у=1, уравнение ![]() корней не имеет т.к. Д 0,
корней не имеет т.к. Д 0,
возвращаясь к переменной х, получим
![]()
Ответ: х=0.
4. Этап. (одновременно с 4) Выполните индивидуальное задание.
Вариант 1.
1. Решите уравнение.
3 6-3х = 27.
2. Решите неравенство.
7 1+3х ≥ 27
О![]() твет.
твет.
Вариант 2.
1. Решите уравнение.
0,3 4-2х = 0,09.
2. Решите неравенство.
![]() .
.
О![]() твет.
твет.
Вариант 3.
1. Решите уравнение.
15 2х+2 = ![]() .
.
2. Решите неравенство.
![]() .
.
О![]() твет.
твет.
Вариант 4.
1. Решите уравнение.
![]()
2. Решите систему.
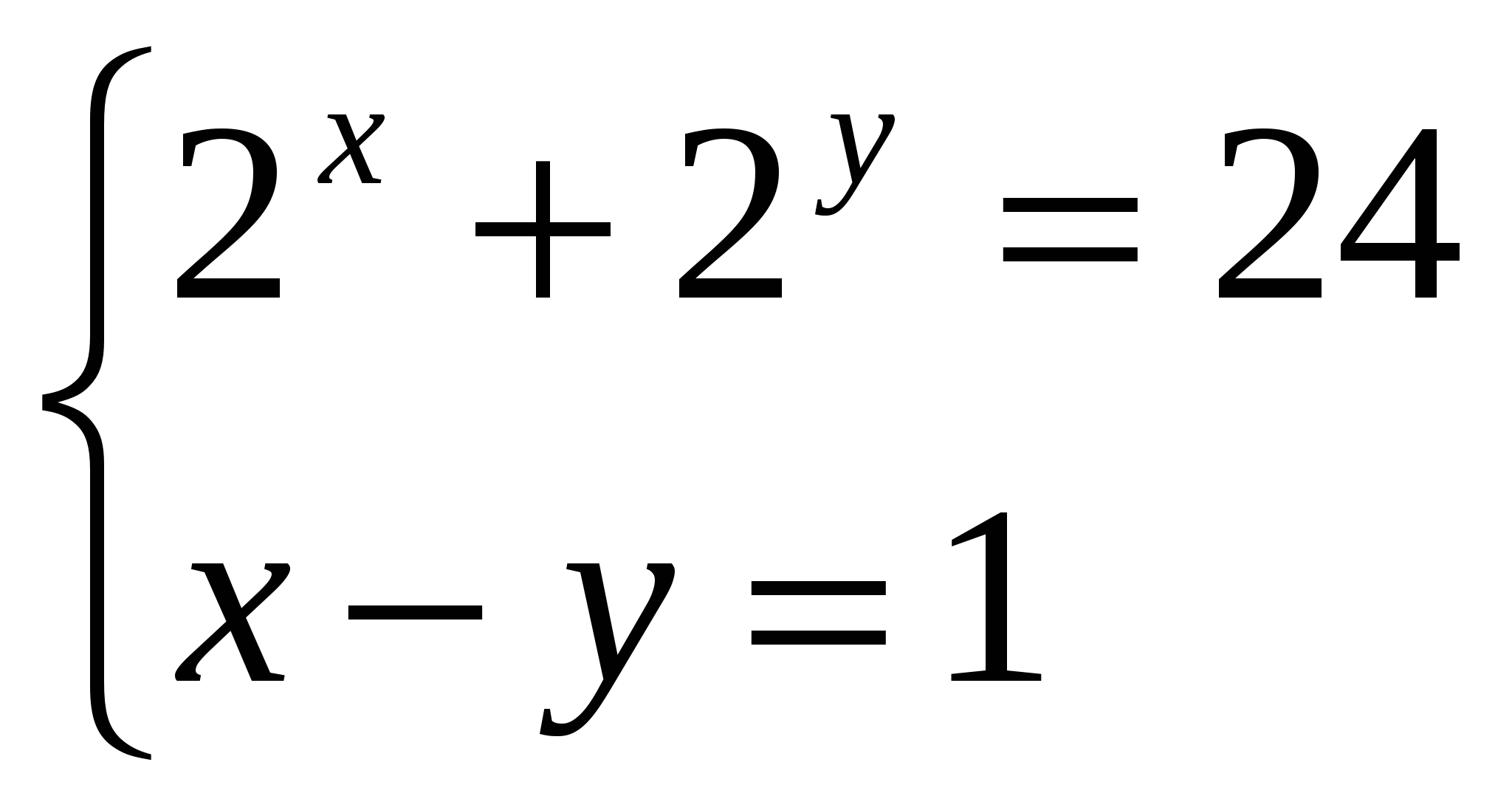
О![]() твет.
твет.
Вариант 5.
1. Решите уравнение.
![]()
2. Решите систему.
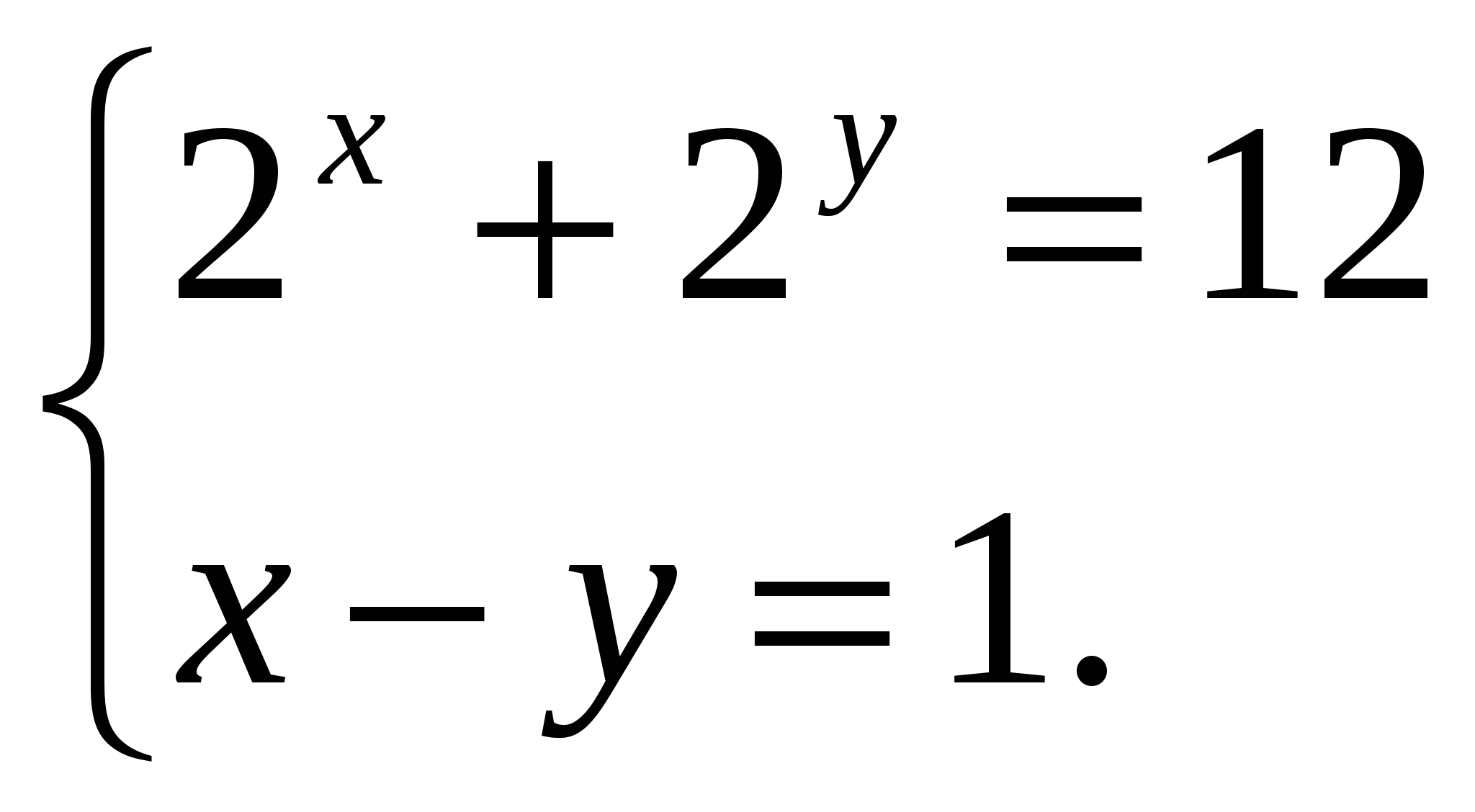
О![]() твет.
твет.
Вариант 6.
1. Решите уравнение.
![]()
2. Решите систему.
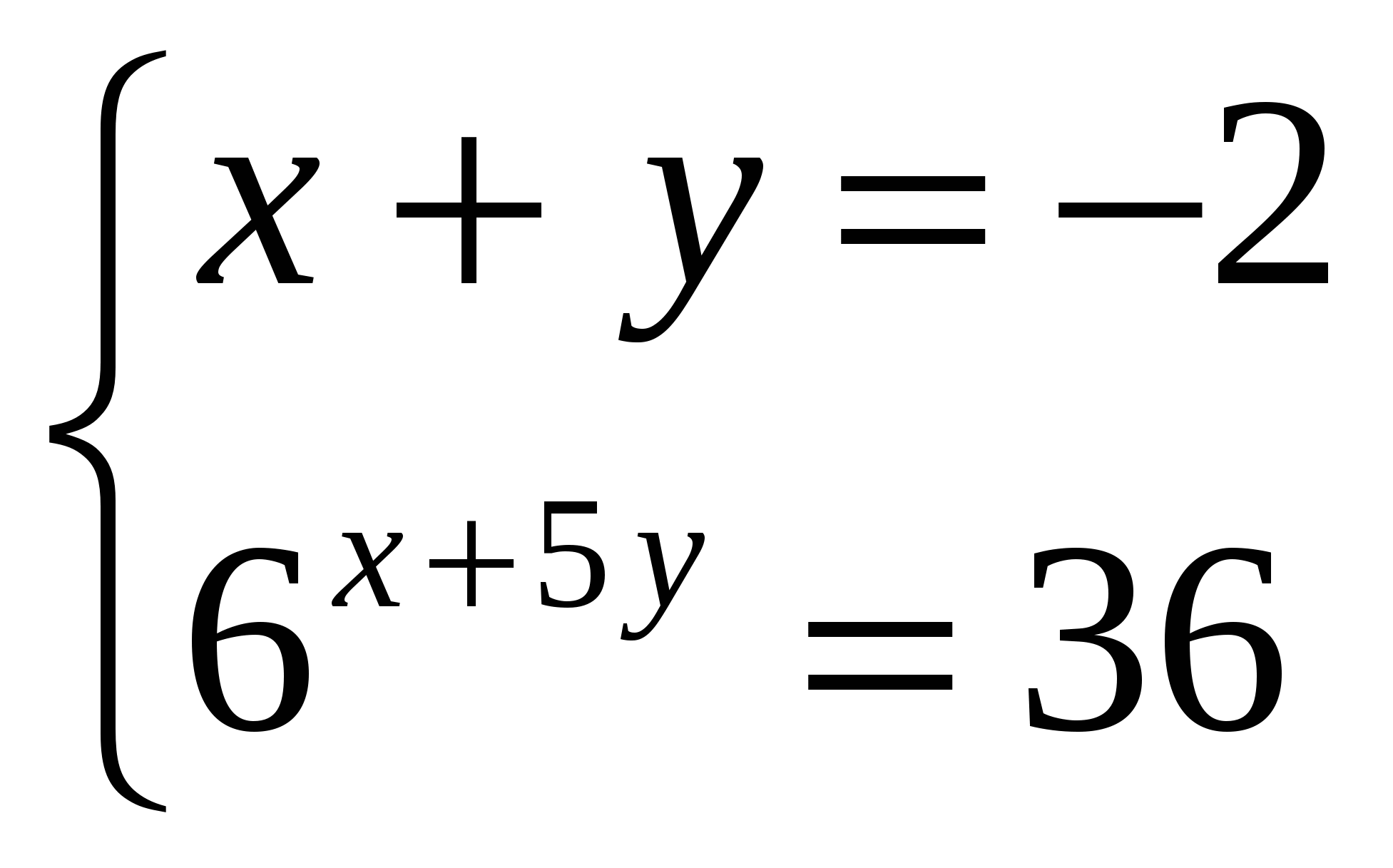
О![]() твет.
твет.
Вариант 7.
1. Решите уравнение.
![]()
2. Решите неравенство.
![]()
![]()
Ответ.
Вариант 8.
1. Решите уравнение.
![]()
2. Решите неравенство.
. ![]() Ответы: (слайд8)
Ответы: (слайд8)![]()
Подведение итогов.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ