Внеклассная работа "Неделя математики"
Муниципальное казённое образовательное учреждение
Холмецкая основная образовательная школа
Оленинского района Тверской области
Внеклассная работа
Неделя математики
Из опыта работы
учителя математики
МКОУ Холмецкой ООШ
Оленинского района
Тверской области
Козловой Т.М.
2012г.
Проведение предметных недель стало хорошей традицией в нашей школе и всегда вызывает у учащихся повышенное внимание и желание поучаствовать в них. Такие мероприятия не только формируют интерес к математике у самого широкого круга школьников, но и возбуждают их к творческой деятельности, способствуют развитию навыков общения, сплачивают детский коллектив.
Цель недели – повысить интерес школьников к изучению предмета, вызвать у них положительные эмоции, подвести к самостоятельным выводам, обогатить кругозор и интеллект учащихся дополнительными знаниями.
Задачи:
- углубление и расширение знаний учебного материала;
-привитие практических навыков;
-ознакомление с историей развития математики;
- использование материала по занимательной математике;
- решение задач повышенной сложности.
За две-три недели в школе создаётся инициативная группа из учеников, проявляющих повышенный интерес к математике. Руководит группой учитель математики. Задачи этой группы – подготовить и провести внеклассные мероприятия с одноклассниками, организовать конкурсы математических кроссвордов, сказок, сочинений, стенгазет. В первый день вывешиваются стенные газеты, сдаются кроссворды, сказки, сочинения и т.п.
Для формирования у учащихся устойчивого интереса к математике необходимо использовать разнообразные формы работы. Опыт показывает, что школьники активнее включаются в игровое взаимодействие. Здесь наряду с познавательными мотивами возникают и другие, которые в явной или неявной форме проявляются в виде желания посоревноваться, общаться во внеурочное время с учителями и товарищами, показать себя перед ними с лучшей стороны, да и просто поиграть развлечься и т.д. С этой целью проводятся математические соревнования, КВН, «Звёздный час», «Счастливый случай» и др.
ПЛАН ПРОВЕДЕНИЯ НЕДЕЛИ МАТЕМАТИКИ
Понедельник
Открытие недели.
Устный журнал по картине Н.П. Богданова-Бельского «Устный счёт»(5-6 кл.)
Вторник
Математические соревнования (5-9кл.)
Среда
Математический КВН(5-6)
Четверг
Игра «Звёздный час»(8-9кл.)
Пятница
Игра «Ключи от форта математика»(7-9кл.)
Подведение итогов недели.
Устный журнал по картине Н.П.Богданова-Бельского «Устный счёт»
СТРАНИЦА ПЕРВАЯ
Картина «Устный счёт» была написана в 1895г. Что изображено на картине? Мальчики собрались около классной доски и что-то рассматривают. Два мальчика (стоят впереди) отвернулись от доски и что-то вспоминают, а может быть считают. Один что-то шепчет на ухо человеку, по-видимому учителю, а другой, кажется, подслушивает.
-А почему они в лаптях?
-А почему тут нет девочек, только одни мальчики?
-А почему они стоят спиной к учителю?
А что они делают?
Вы уже, верно, поняли, что здесь изображены учащиеся и учитель. Конечно, костюмы учащихся необычные: некоторые ребята в лаптях, а у одного из героев картины (того, который изображён на переднем плане) и рубаха порвана. Ясно, что эта картина не из нашей школьной жизни. Вот и надпись на картине: 1895 год – время старой дореволюционной школы. Крестьяне жили тогда бедно, сами они и их дети ходили в лаптях. В то время мало кто из них мог учиться даже в начальной школе. Посмотрите-ка на картину: ведь только трое из учащихся в лаптях, а остальные – в сапогах. Очевидно, ребята из богатых семей. Ну, а почему на картине не изображены девочки, это тоже не трудно понять: в то время девочек, как правило, в школу не принимали. Ученье было «не их делом», да и мальчики-то учились далеко не все.
СТРАНИЦА ВТОРАЯ
Эта картина называется «Устный счёт». Посмотрите, как сосредоточенно думает мальчик, изображённый на переднем плане. Видно, нелёгкую задачу дал учитель. Но этот ученик, наверное, скоро закончит работу, ошибки не должно быть: уж очень серьёзно относится к устному счёту. А тот, который что-то шепчет на ухо учителю, кажется, уже решил задачу, только его ответ не совсем правильный. Смотрите: учитель слушает ученика внимательно, но на лице нет одобрения, значит, ученик сделал что-то не так. А может быть, учитель терпеливо ожидает, когда и другие сосчитают, и потому не спешит одобрить его ответ?
-Нет, первым даст правильный ответ тот, кто стоит впереди: сразу видно, что он лучший ученик в классе.
А какую же задачу дал им учитель? Не сможем ли решить её и мы? На доске я запишу задачу так, как привыкли писать вы:
(10·10+11·11+12·12+13·13+14·14): 365.
Как видно, каждое из чисел 10, 11, 12, 13 и 14 нужно умножить само на себя, результаты сложить, а полученную сумму разделить на 365.
-Вот так задача! Такой пример не скоро решишь, да ещё в уме.
А всё-таки попробуйте сосчитать устно, в трудных местах я буду помогать вам. Десятью десять – сто, это каждый знает. Одиннадцать умножить на одиннадцать – это тоже нетрудно сосчитать: 11·10=110, да ещё 11, всего 121. Умножая 12 на 12, поступаем так: 12·10=120, да ещё 12·2=24, а всего будет 144.
Действуя аналогично, получим: 13·13=169 и 14·14=196.
Но пока мы умножали, то почти забыли, какие числа получились ранее. Потом я вспомню их, а ведь эти числа надо ещё сложить, да потом сумму разделить на 365. Придётся вам немного помочь. Какие же числа у нас получились?
-100, 121, 144, 169 и 196.
-Теперь вы, наверное, хотите сложить все пять чисел, а потом уже делить результат на 365?Давайте мы это сделаем по-другому. Ну-ка, сложим первые три числа: 100, 121 и 144.Сколько получится?
-365.
А делить на сколько надо?
-Тоже на 365.
-Сколько же получится, если сумму первых трёх чисел разделить на 365?
-Один!
Теперь сложите остальные два числа: 169 и 196. Сколько получится?
-Тоже 365!
Вот так пример, и совсем нехитрый. Получается-то всего лишь два! Только для его решения надо хорошо знать, что сумму можно делить не сразу всю, а каждое слагаемое в отдельности или же по группам в два три слагаемых, а потом уж сложить получившиеся результаты.
СТРАНИЦА ТРЕТЬЯ
Картина называется «Устный счёт». Написал её художник Николай Петрович Богданов-Бельский (1868-1945).
Богданов-Бельский очень хорошо знал своих маленьких героев: вырос в их среде, был когда-то пастушком. «Я незаконнорожденный сын бедной бобылки, оттого Богданов, а Бельским стал по имени уезда», - рассказывал художник о себе.
Ему посчастливилось попасть в школу известного русского педагога С.А.Рачинского, который заметил художественный талант мальчика и помог ему получить художественное образование.
Н.П. Богданов-Бельский окончил Московское училище живописи и зодчества, учился у таких известных художников, как В.Д. Поленов, В.Е. Маковский.
Немало портретов и пейзажей написано Богдановым-Бельским, но в памяти он остался, прежде всего, как художник, сумевший поэтично и верно поведать осмышлённой сельской детворе, жадно тянущейся к знаниям.
«У дверей школы», «Новичок», «Сочинение», «Деревенские друзья», «У больного учителя», «Проба голоса» - вот названия лишь некоторых его картин. На них чаще всего художник изображал детей в школе. Прелестные, доверчивые, сосредоточенные, задумчивые, полные живого интереса и всегда отмеченные природным умом – такими знал и любил крестьянских детишек Богданов-Бельский, такими увековечил в своих произведениях.
СТРАНИЦА ЧЕТВЁРТАЯ
Художник изобразил на этой картине невыдуманных учеников и учителя. Учитель – Сергей Александрович Рачинский, известный русский педагог, замечательный представитель русских образованных людей позапрошлого века. Он был доктором естественных наук и профессором ботаники Московского университета. В 1968 г. С.А. Рачинский решает «уйти в народ». Он держит экзамен на звание учителя начальных классов. На свои средства открывает школу для крестьянских детей в селе Татево Смоленской губернии и становится в ней учителем. Его ученики так хорошо считали устно, что этому удивлялись все посетители школы. Не случайно художник изобразил С.А. Рачинского вместе с его учениками на уроке устного решения задач.
Это картина – гимн учителя и ученику.
Математические соревнования
1. Конкурс «Занимательные задачи».
Е
В. 5
сли у стола отпилить один угол, то сколько углов останется?
А. 3 Б. 4 Г. Нисколько.
С
Г. Нисколько.
колько минут надо варить крутое яйцо?
А. 2 мин. Б. 3 мин. В. 5 мин.
В
А. 2
комнате горело 5 свечей. Две из них потухли. Сколько свечей осталось?
Б. 3 В. 5 Г. Нисколько.
В. 5
В комнате горело 5 лампочек. Две из них перегорели. Сколько лампочек осталось?
А. 2 Б. 3 Г. Нисколько.
С
А. 3
колько раз в сказке А.С.Пушкина «Сказка о рыбаке и рыбке» старик ходил к морю просить рыбку исполнить его пожелание?
Б. 5 В. 7 Г. Нисколько.
З
В. 11
айцы пилят бревно. Они сделали 10 распилов. Сколько получилось чурбачков?
А. 2 Б. 3 Г. Нисколько.
Н
В. 3
а столе стояли три стакана с ягодами. Вова съел один стакан и поставил его на место. Сколько стаканов осталось на столе?
А. 1 Б. 2 Г. Нисколько.
Как называется явление природы, когда луна находится между Солнцем и Землей на одной прямой?
Б. Солнечное затмение
Г. Затмение мозгов.
2. Конкурс «Черный ящик».
В ящике лежит какой–то предмет. Ведущий дает его словесное описание. Команде надо указать, что лежит в ящике?
Это предмет очень полезен, он устраняет неточности, делает работу более аккуратной. Имеет различные формы, цвета, даже запахи. Но в основном бело-серого цвета, форма – параллелепипед, размеры – небольшие.
(Ластик или резинка)
Этот предмет – незаменимый помощник, но если знаешь, как им пользоваться. В основном используются маленькие по размерам модели с небольшим числом стандартных функций. Но бывают более функциональные модели, если его встраивают в другие предметы – например, часы, органайзер и т.д.
(Микрокалькулятор.)
3. Конкурс «Ассоциация».
Капитану на ушко сообщается какое-то слово. Он называет ведущему на ушко 8 слов, ассоциативно связанных с данным. Затем ведущий сообщает ключевое слово всей команде. Каждый член команды называет по одной своей ассоциации этого слова. Жюри учитывает все совпадения.
Пример: 1.параллелепипед (спички, кирпич, мыло, книга, …)
2. окружность (солнце, монета, кольцо …)
3. шкала (весы, линейка, термометр …)
4. «Конкурс рисунков».
Изобразите смешанную фигуру по данным ведущего: время – 3 мин.
Составьте фигуру из двух лучей, угла в
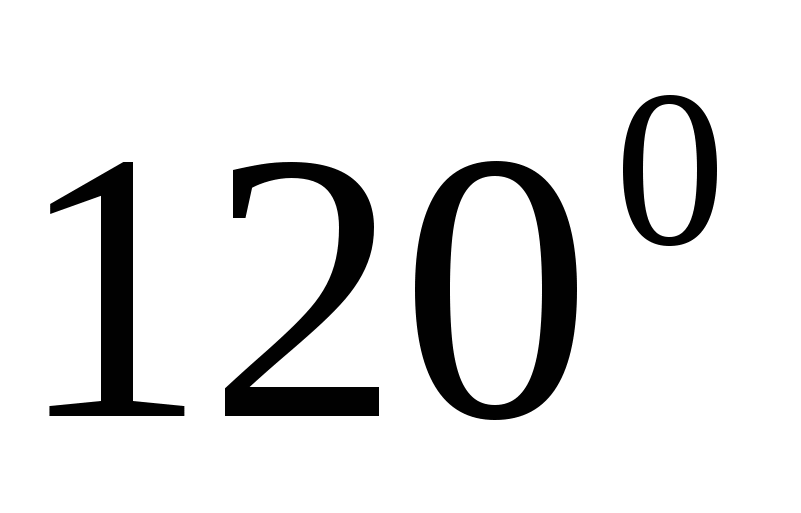 , равнобедренного треугольника, окружности и двух отрезков.
, равнобедренного треугольника, окружности и двух отрезков.Составьте фигуру из квадрата, прямоугольника, равнобедренного тупоугольного треугольника и прямых углов.
5. Конкурс «Эрудит».
Предлагаются логические задачи.
Встречаются три подруги – Белова, Краснова и Чернова. На одной из них было черное платье, на другой – красное, на третьей – белое. Девочка в белом платье говорит: «Нам надо поменяться платьями, а то у всех троих цвет платья не соответствует фамилии». Кто в какое платье был одет?
Ответ: Белова – в черное,
Чернова – в красное,
Краснова – в белое.
В кафе встретились три друга: скульптор Белов, скрипач Чернов, художник Рыжов. «Замечательно, что у одного из нас белые, у другого – черные, а у третьего – рыжие волосы, но ни у кого цвет волос не соответствует фамилии», - заметил черноволосый. «Ты прав», - сказал Белов. Какой цвет волос у каждого из друзей?
Ответ: у Белова – рыжие,
у Чернова – белые,
у Рыжова – черные.
6. Конкурс «Домашнее задание».
Команды обмениваются подготовленными кроссвордами, разгадывают их, а болельщики должны вспомнить и записать как можно больше математических терминов, начинающихся с букв «Т», «П» и «М».
Кроссворд №1.

По вертикали: 1. Наука об измерении треугольников. 2. Тысячная доля миллиметра. 3. величина, характеризующая не только числовым значением, но и направлением. 4. Самая большая хорда. 5. Немецкий математик.
По горизонтали: 6. Счетная машина. 7. Расстояние между концами пальцев, разведенных в стороны рук. 8. Ширина ладони на уровне пальцев. 9. Произведение числовых и буквенных множителей.
Кроссворд №2.

По горизонтали: 1. Трехзначное число. 3. Старинная русская единица длины. 8. Единица измерения времени. 9. Математическое действие. 10. Равенство, содержащее букву. 13. Тысячная часть числа. 14. Десятая часть основной единицы длины.
По вертикали: 2. Буква латинского алфавита. 4. Черта на шкале. 5. Неметрическая мера объема. 6. Старая русская мера объема. 7. Наименьшее натуральное число. 11. Образцовое средство измерения. 12. Объем килограмма воды.
7. Конкурс «Математический калейдоскоп».
Игра «В мире звезд»
Решение линейных уравнений, 8–9 кл.
б) Степень с натуральным показателем, 7–9 кл.
Игра «Мозаика»
а) Деление, 5–9 кл.
б) Проценты, 6–9 кл.
Игра «Индийское письмо»
Квадратные корни, 8–9 кл.
Игра «В мире звезд»
№ 1. Тема: Решение линейных уравнений.
Перед вами фрагмент карты звездного неба (см. рис.). Найдите на нем созвездие Близнецы. Для этого выполните задания и соедините последовательно звезды, которым соответствуют найденные ответы.

Задания.
1 – 4. Решить уравнения:
1) ![]() ; 3)
; 3) ![]() ; 2)
; 2) ![]() ; 4)
; 4) ![]() .
.
5. Восстановите правую часть по его сохранившемуся решению:
![]() ,
,
![]() .
.
При каком значении переменной: а) значения выражения
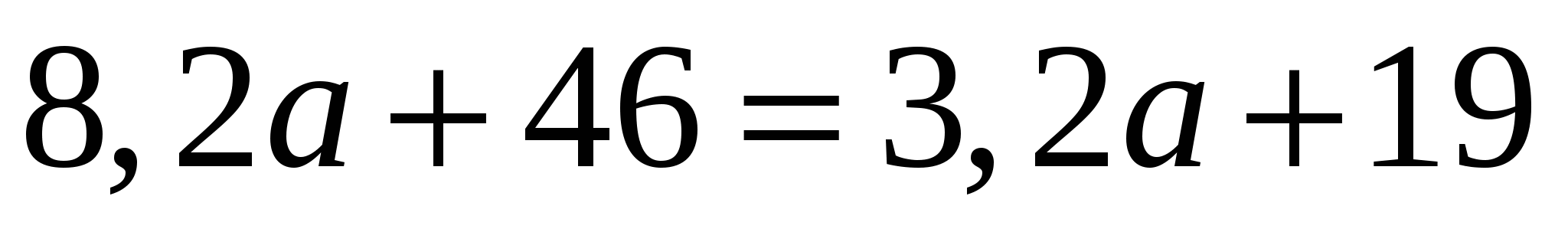 ; б) значение выражения
; б) значение выражения 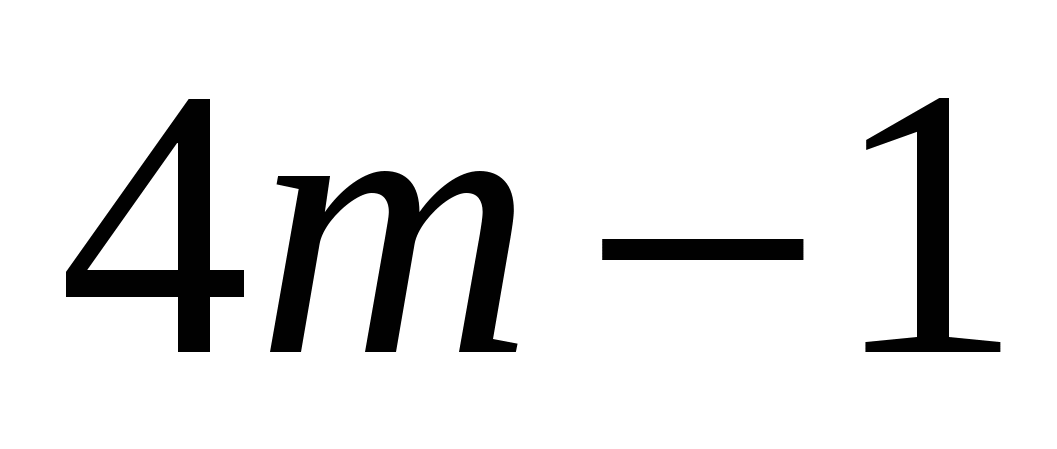 на
на 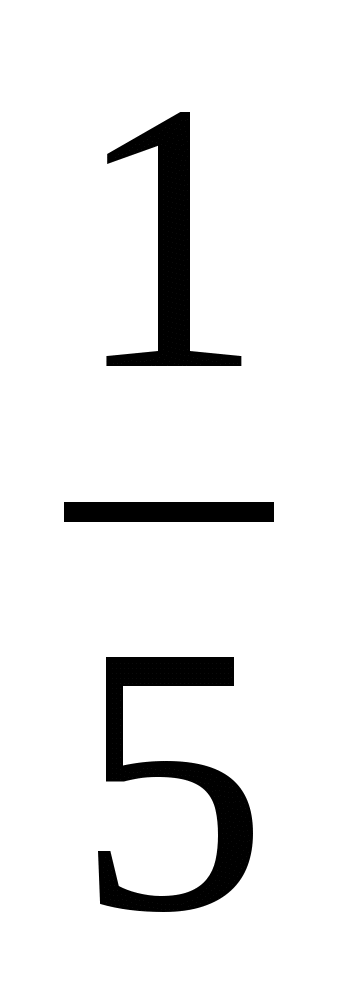 больше значения выражения
больше значения выражения 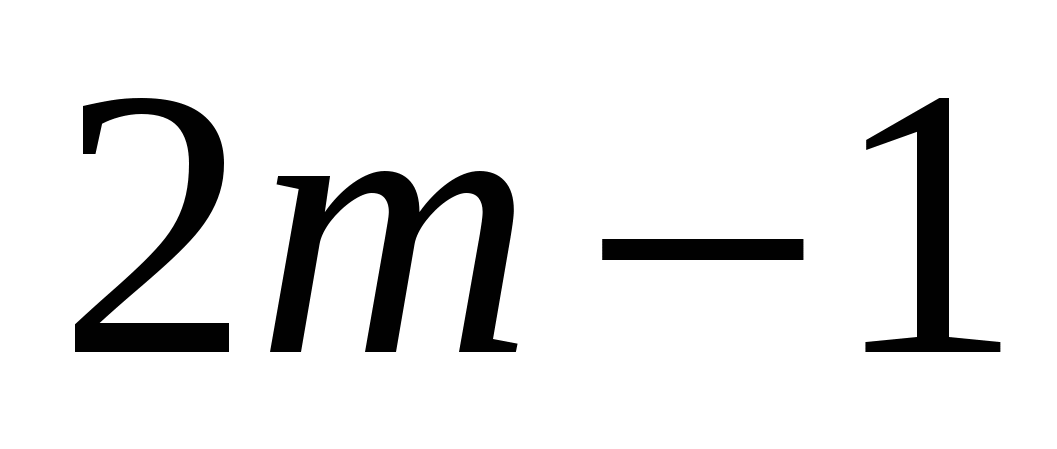 ?
?
№ 2. Тема: Степень с натуральным показателем.
Найдите на карте (см. рис.) созвездия Цефей и Кассиопия. Для этого выполните задания и соедините последовательно звезды, которым соответствуют найденные ответы.
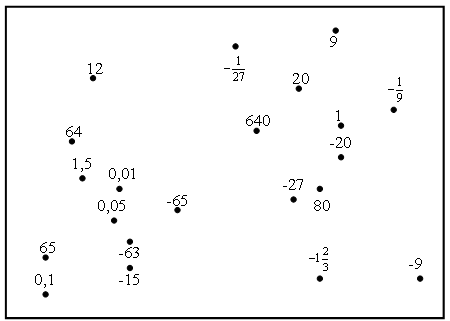
Задания.
1 – 6. Вычислите.
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ;6)
;6) ![]() .
.
1 – 5. Найдите значение выражения.
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
;
4) ![]() ; 5)
; 5) ![]() .
.
Игра «Мозаика»
Тема: Деление.
Восстановите фрагмент мозаики (см. рис.). Для этого решите примеры и раскрасьте элементы мозаики, содержащие правильные ответы. Каждый ответ нужно раскрасить столько раз, сколько он встречается в узоре.
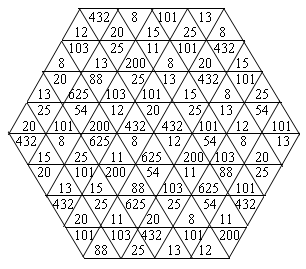
Задания:
Найдите частное чисел 72 и 6.
Чему равен делитель в частном
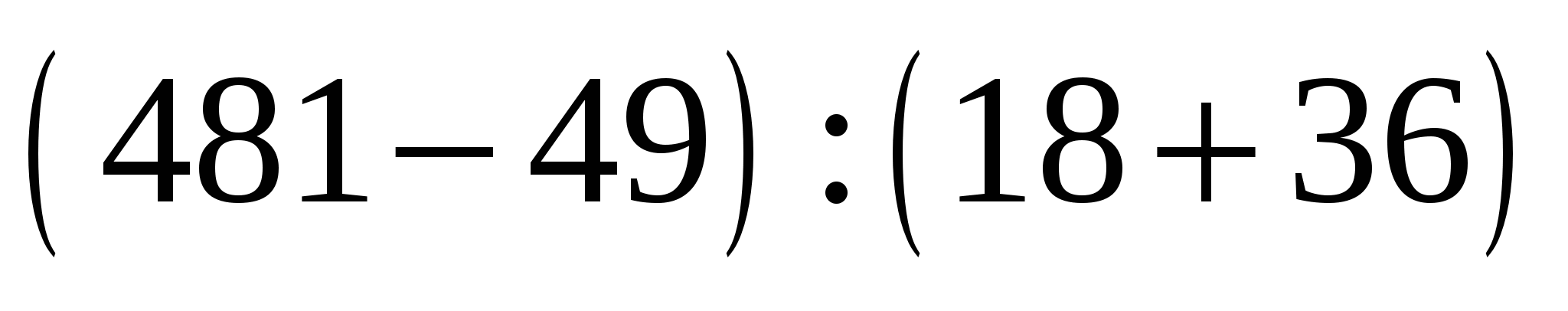 ?
?Во сколько раз 11 меньше 121?
Решите уравнение
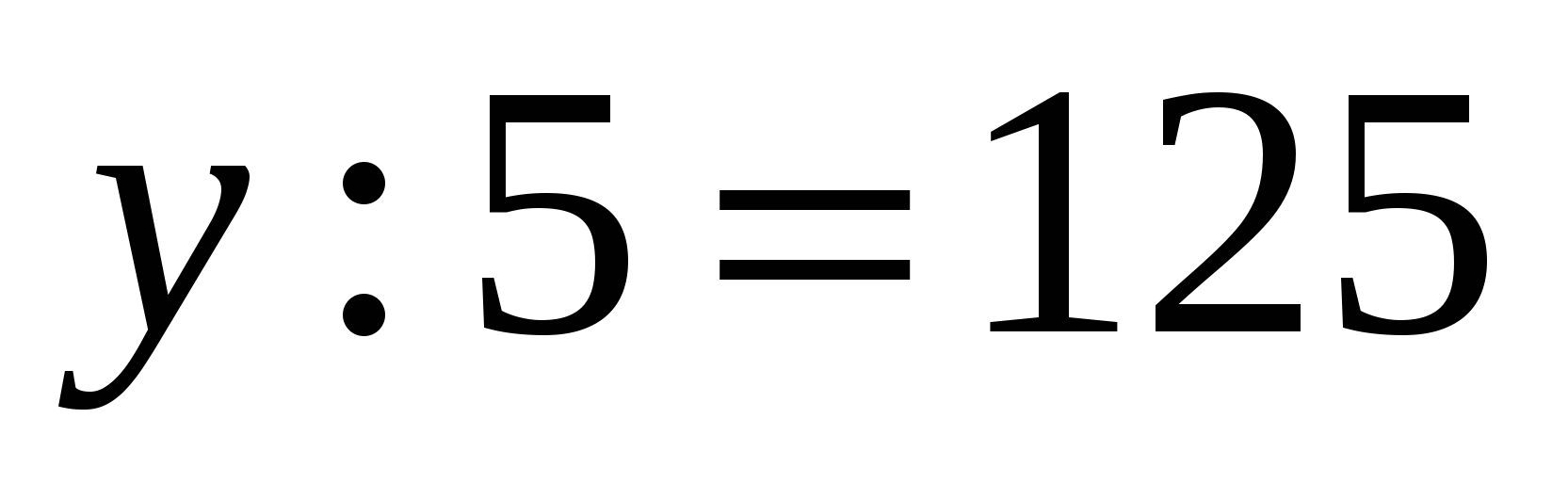 .
.Решите уравнение
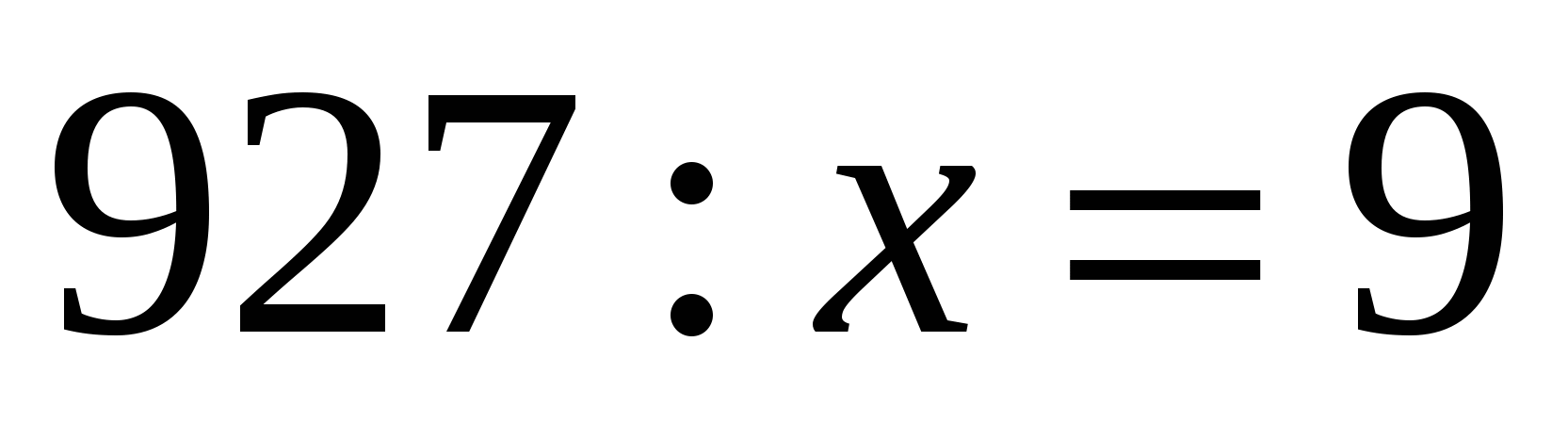 .
.Найдите значение выражения
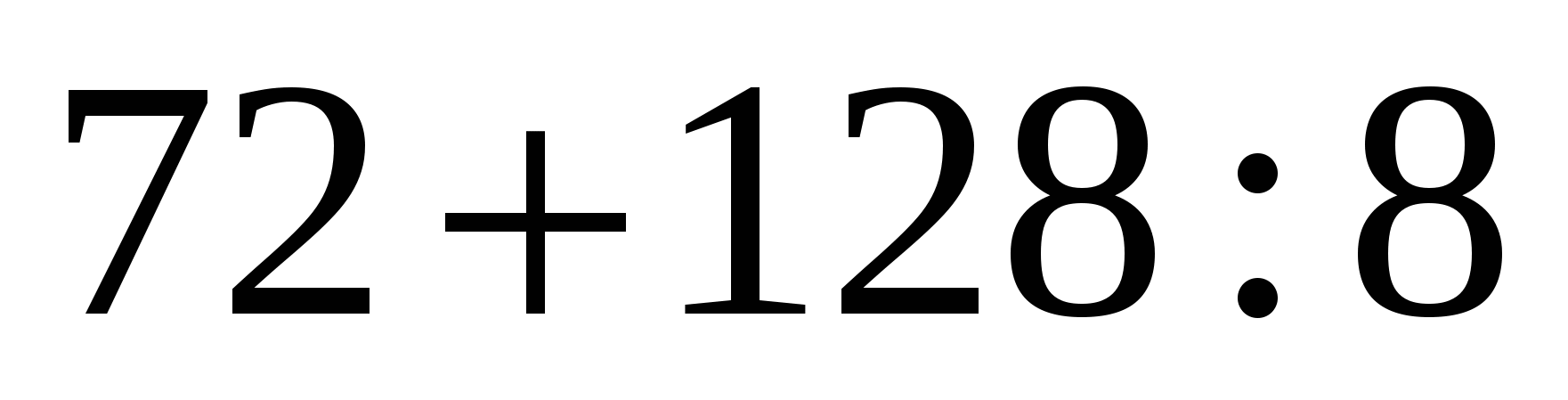 .
.Найдите значение выражения
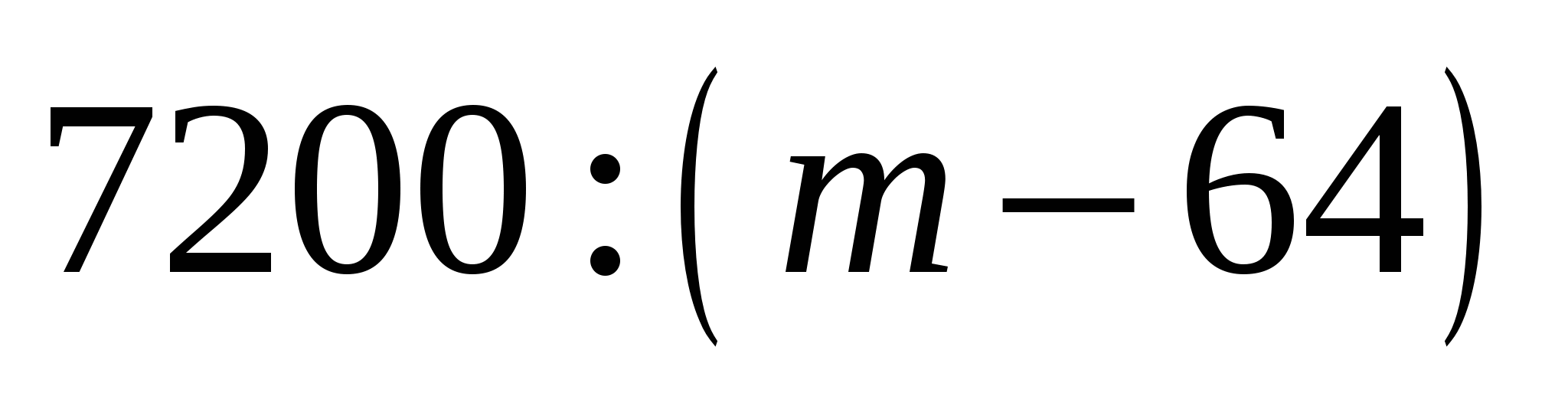 при
при 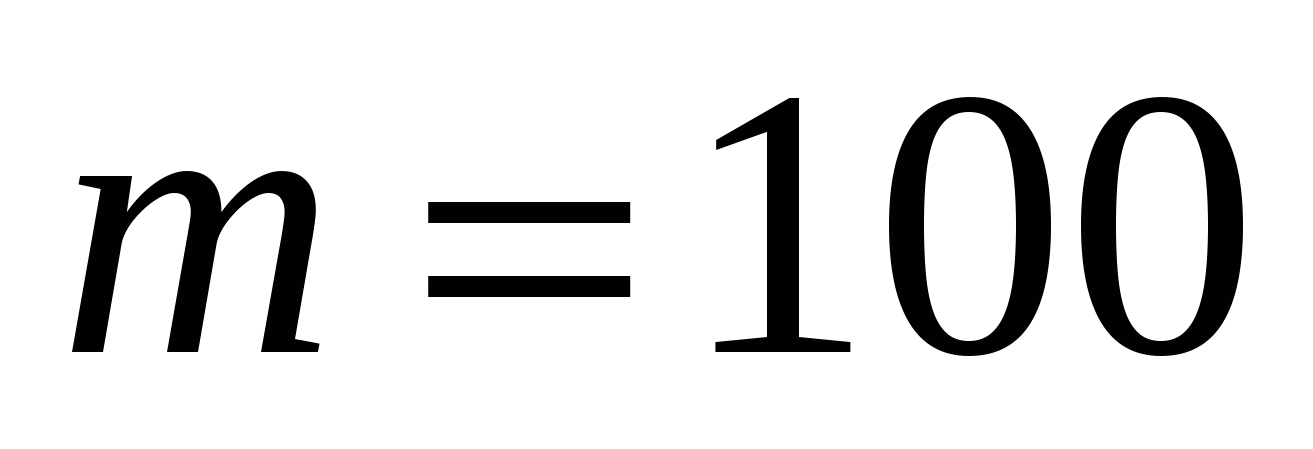 .
.
Тема: Проценты.
Восстановите фрагмент мозаики (см. рис.). Для этого решите примеры и раскрасьте элементы мозаики, содержащие правильные ответы. Каждый ответ нужно раскрасить столько раз, сколько он встречается в узоре.
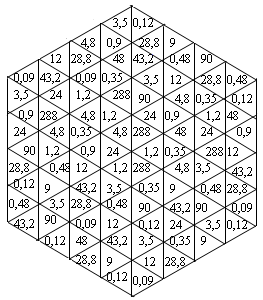
Задания:
Выразить в виде десятичной дроби:
а) 35 %; б) 480 %.
Вычислите:
а) 12 % от числа 7,5; б) 0,3 % от числа 400.
Найдите число:
а) 45 % которого равны 10,8; б) 250 % которого равны 720.
Сколько процентов числа 36 составляет от числа 75?
Игра «Индийское письмо»
Тема: Квадратные корни.
Перед вами индийское письмо «в картинках» (см. рис.). Выполнив задания и выбрав из предложенных вариантов ответов правильные, расшифруйте послание. Номера рисунков совпадают с номерами заданий, а сами рисунки обозначают слова, которым соответствуют верные ответы.
Замечание. При формулировании послания разрешается склонять слова и вставлять предлоги и союзы (по смыслу).
1 2 3 4

5 6 7
Задания:
Вычислите
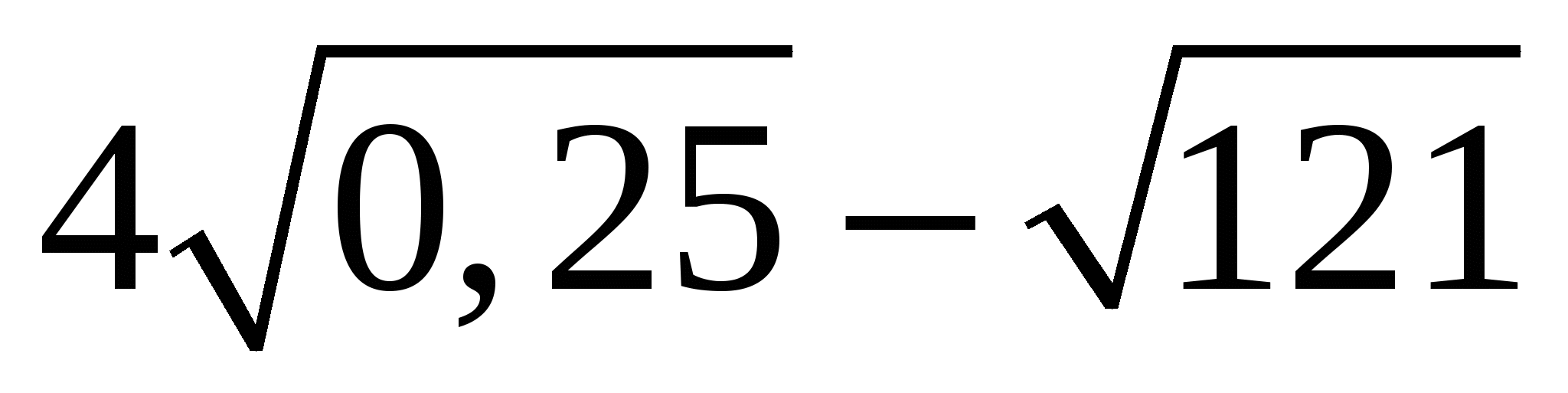 .
.Вычислите
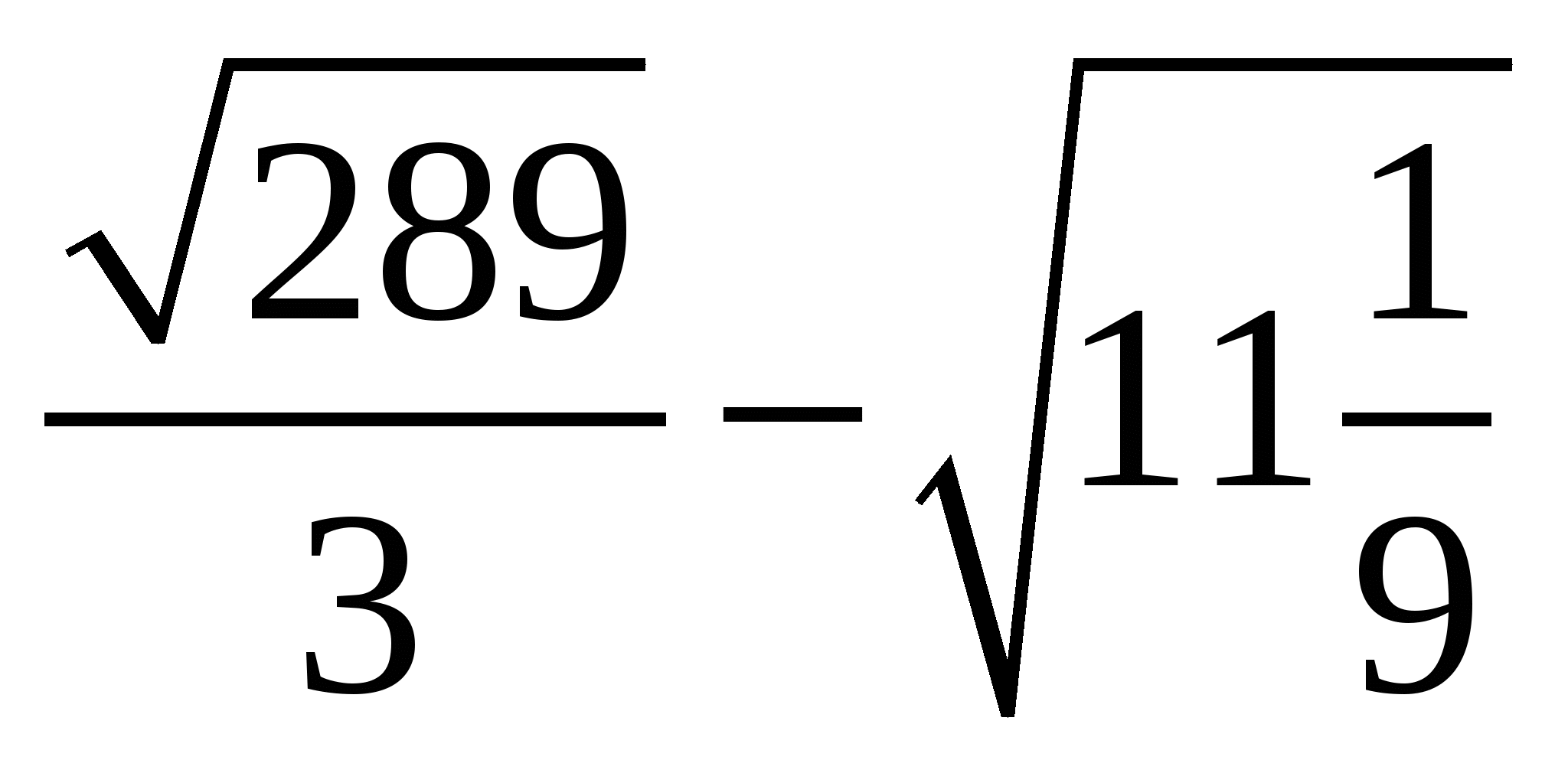 .
.Найдите значение выражения
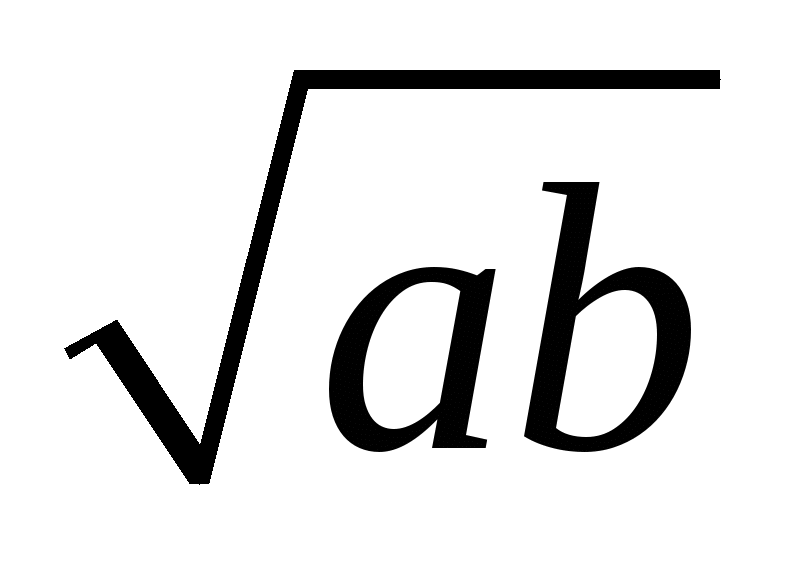 при
при  и
и 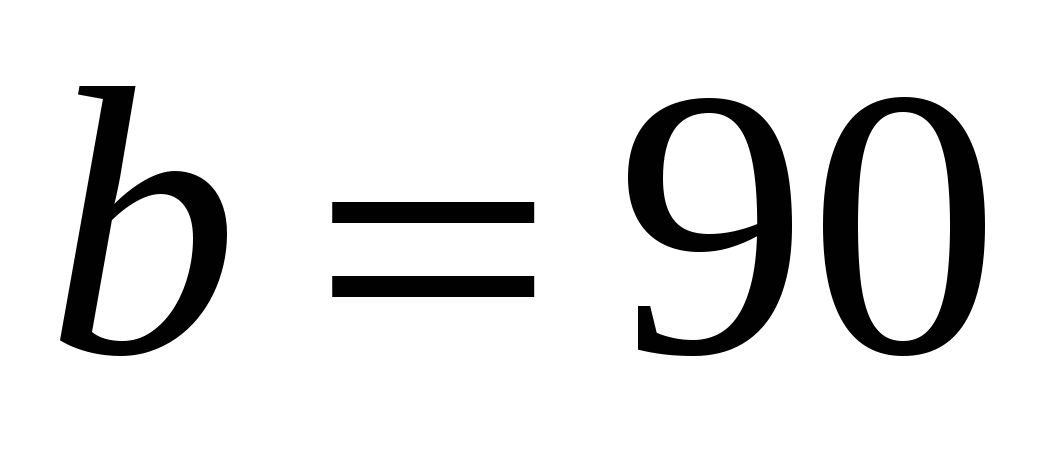 .
.Найдите значение выражения
 при
при 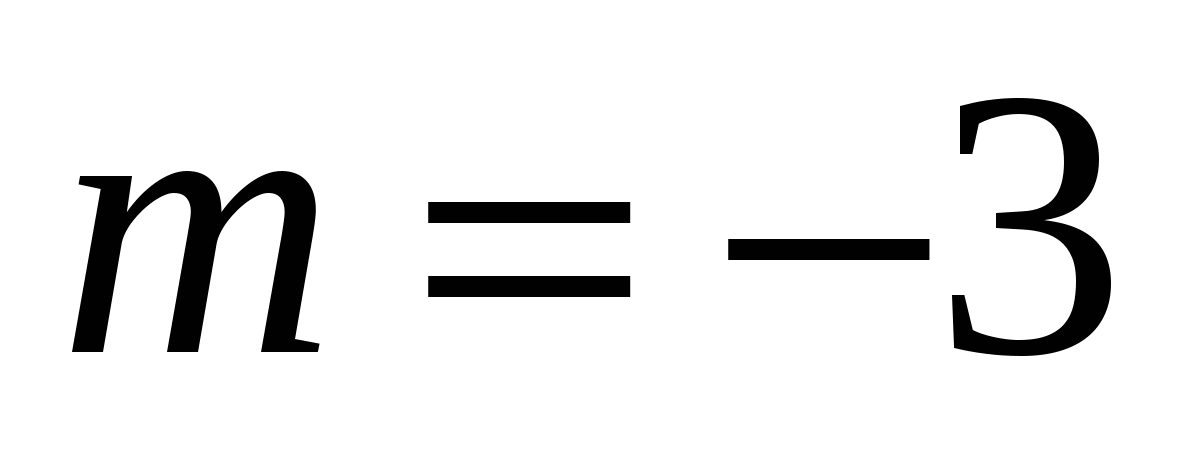 .
.Внесите множитель под знак корня:
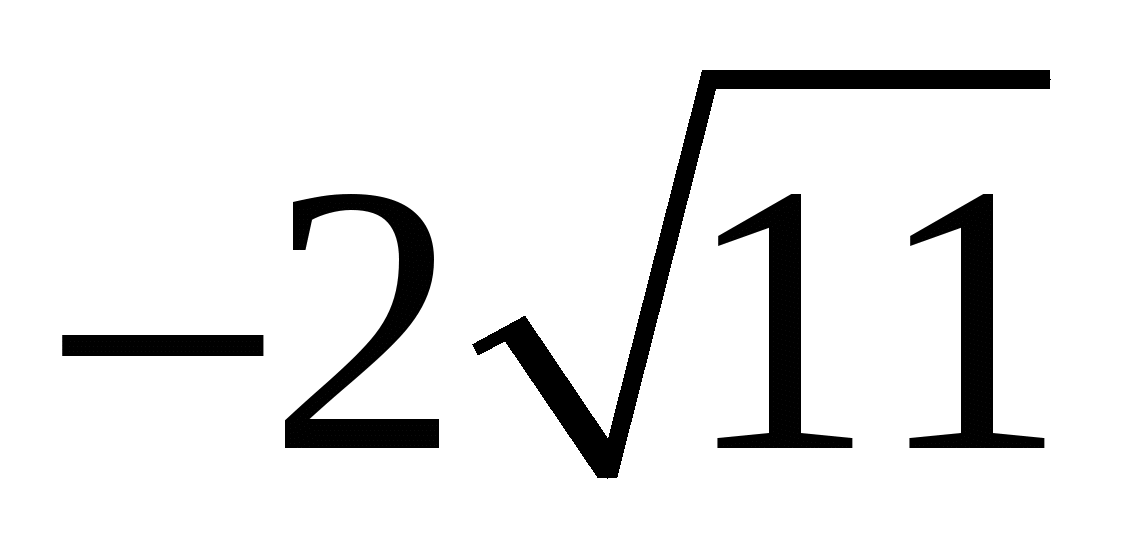 .
.Вынесите множитель из-под знака корня:
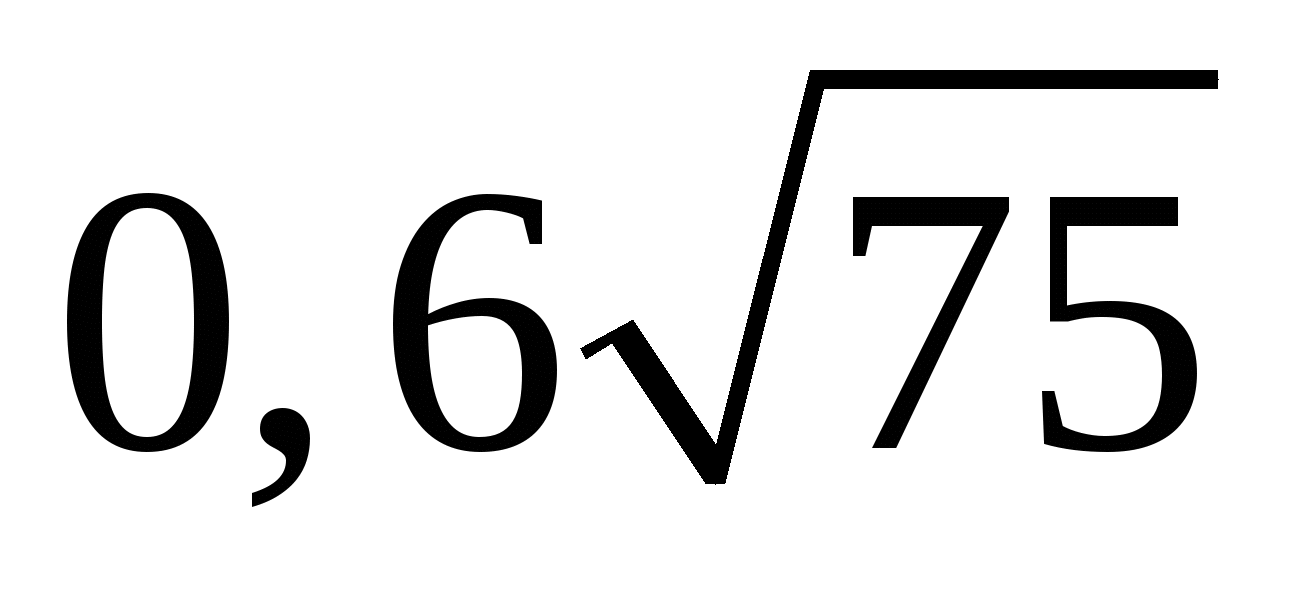 .
.Какое из чисел больше:
 или
или 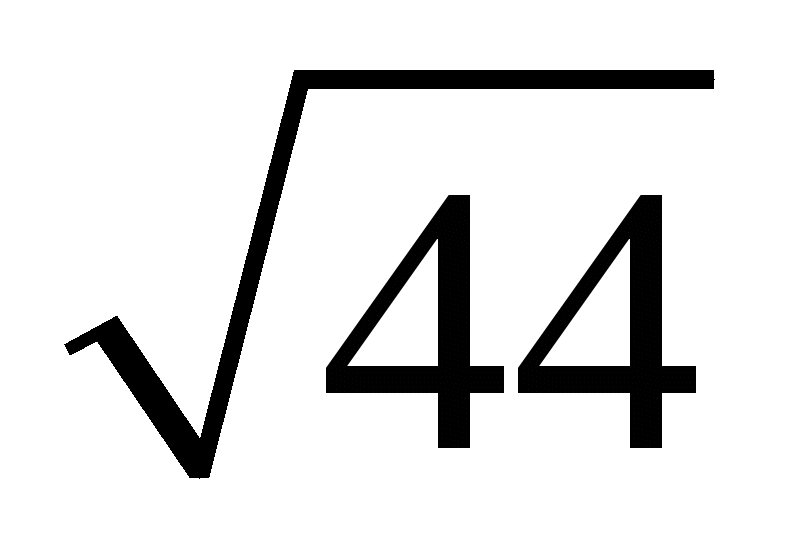 ?
?
Варианты ответов
Слова
![]()
Воскресенье
![]()
День
![]()
Ливень
![]()
Луна
![]()
Вторник
![]()
Солнце
![]()
Вчера
![]()
Обед
![]()
Дождь
![]()
Утро
![]()
Ночь
![]()
Град
![]()
Сегодня
![]()
Ясная погода
![]()
Звезда
8. Конкурс «Задачи-шутки на сообразительность».
В полдень из Москвы в Тверь выехала грузовая машина со скоростью 60 км/ч. Часом позже из Твери в Москву выехал мотоцикл со скоростью 30 км/ч. Когда они встретятся, кто будет дальше от Москвы?
(на одном расстоянии)
Электропоезд идет с востока на запад со скоростью 15 км/ч. Ветер дует с запада на восток со скоростью 30 км/ч. В какую сторону будет отклоняться дым от электропоезда?
(у него нет дыма)
Математический КВН
Участники игры
Команды (в составе 8–10 человек) двух классов.
Ведущий – учитель математики или ученик старшего класса.
Жюри – по одному ученику от класса (выбираются командами), учителя математики, старшеклассники, возможно, классные руководители и родители.
На КВНе присутствуют также болельщики и зрители – ученики разных классов.
Реквизит
Листы бумаги, карандаши, спички, четыре монеты одинакового достоинства, карточки с заданиями, плакаты с записью сочетательного и переместительного свойств сложения чисел.
Задача игроков – правильно и как можно быстрее отвечать на вопросы ведущего и выполнять предложенные задания.
Каждый конкурс оценивается в баллах.
Время проведения КВНа – 60–70 мин.
Ход игры
Ведущий приветствует команды и объявляет состав жюри.
Этап 1. Представление команд
Это конкурс-презентация участников. К нему игроки готовятся заранее: придумывают название и эмблему команды.
Высшая оценка за конкурс – 5 баллов.
Этап 2. Разминка
Каждый правильный ответ на вопрос «Разминки» оценивается 1 баллом.
Сначала команды должны поочередно ответить на следующие вопросы.
Как называется второй месяц лета?
Как называется второй месяц зимы?
Представьте себя в роли столяра. Вам необходимо отпилить у четырехугольной крышки стола один угол. Сколько углов останется у крышки?
Чтобы распилить доску на несколько одинаковых частей, столяр сделал на ней 5 отметок. Сколько кусков получится из доски?
Какими двумя цифрами оканчивается произведение
1∙2∙3∙4∙5∙6∙7∙8∙9∙10∙11∙12∙13?![]()
Чему равна сумма
(– 100 – 99 – 98 – 97 – ... – 1) + (1 + 2 + 3 + … + 100)?
Ещё на два вопроса отвечают обе команды (кто быстрее).
Вам надо сварить яйцо всмятку. Известно, что всмятку яйцо варится 4 мин. У вас есть двое песочных часов: одни отмеряют 3 мин, а другие – 7 мин. Как, пользуясь этими часами, варить яйцо точно положенное время?
Двое рабочих собрались поехать на электричке за город и договорились встретиться в пятом вагоне, но забыли уточнить, откуда его считать – от начала или от конца поезда. В результате один сел в пятый вагон от начала, а другой от конца. И все-таки друзья встретились. Сколько вагонов было в поезде?
Этап 3. Конкурс капитанов.
Третий конкурс – индивидуальный. Капитанам команд предлагается ответить на ряд вопросов. При этом оцениваются быстрота и правильность ответа; за каждый верный ответ присуждается 1 балл.
Вопросы
Сколько получится, если вычесть из числа –2 число, противоположное уменьшаемому?
Яйцо всмятку варится 4 мин. А сколько времени нужно, чтобы сварить всмятку 5 яиц?
Заяц вытащил 8 морковок и съел их все, кроме 3. сколько морковок осталось?
Выглянув на повороте в окно поезда, Таня заметила перед собой 7 вагонов, а позади ещё 5. Сколько всего вагонов в этом поезде?
Одна машина перевозит 4 бетонные плиты. Сколько машин потребуется, чтобы перевезти 13 таких же плит?
В автобус сели 10 человек. На первой остановке вышли 5 пассажиров, а вышли 3. на следующей остановке вышли 5 человек, а вошли 12. затем никто не выходил, зато вошли 2 человека. Наконец, на конечной остановке вышли все пассажиры. Сколько всего было остановок?
Этап 4. Командные конкурсы
На следующем этапе КВНа проводится серия конкурсов, а также игры с болельщиками.
Продолжи ряд
Задание. Проанализируйте ряды чисел, выявите закономерность и продолжите каждый ряд.
3, 4, 8, 16, 32, …
1, 3, 4, 7, 11, 18, …
За верный ответ дается 1 балл, а за неверный – снимается 1 балл.
Инсценировка
Задание. Одной команде предлагается инсценировать сочетательное свойство сложения, а другой – переместительное (кому какое свойство достанется, определяется с помощью жребия). На подготовку дается 5–7 мин.
Высшая оценка в этом конкурсе – 3 балла.
Пока команды готовятся к выступлениям, проводятся игры с болельщиками.
Ведущий перечисляет натуральный ряд чисел. Болельщики хлопают, если число содержит в записи цифру 3 или делится на 3. побеждает тот, кто меньше всех ошибется.
Болельщики поочередно вспоминают математические правила. Выигрывает тот, кто скажет правило последним.
В обоих случаях победитель приносит своей команде один балл.
Прямоугольники из спичек
Задание. У вас есть 14 спичек. Выясните, сколько различных прямоугольников можно сложить из них?
В этом задании оцениваются быстрота и правильность решения. Максимальный балл равен 2.
Проверка глазомера
Задание. Даны две одинаковые монеты. Одна из них совершает полный оборот вокруг другой, соприкасаясь с ней. Сколько раз при этом движении первая монета обернется вокруг своего центра? Сначала дайте ответ, а затем проверьте его с помощью монет на ваших столах.
Правильный ответ оценивается в 2 балла.
Шифровка
Задание. С помощью табл. 4 прочитайте полезный совет, зашифрованный в табл. 3.
Е
Д
Д
И
Й
Г
А
У
И
Н
Е
Н
К
Й
Т
Е
А
В
Д
Р
О
З
Р
Е
А
9
20
13
2
17
5
16
22
10
8
12
1
3
25
18
19
7
15
6
21
4
23
11
24
14
Таблица 3. Таблица 4.
Во время конкурса проводится ещё одно состязание среди болельщиков.
Детям предлагается вспомнить известные книги и фильмы, в названиях которых встречаются числительные.
Команде, чей болельщик озвучит название последним, добавляется 1 балл.
Составь слова
Задание. Составьте как можно больше слов из букв, входящих в слово ТРЕУГОЛЬНИК.
На задание дается 3 мин. Команда, назвавшая слово последней, получает 1 балл. (В этом конкурсе разрешается помощь болельщиков.)
Этап 5. Награждение победителей
Жюри подсчитывает баллы, подводит итоги, объявляет победителей.
За 1 и 2 место даются грамоты. Также призами отмечается самый внимательный игрок, самый сообразительный игрок и самый активный болельщик.
Игра «Звездный час».
Оборудование: карточки с цифрами 1, 2, 3, 4, 5, 6, 7, 8.
I тур.
Н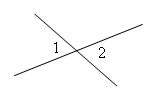
 а доске восемь геометрических фигур.
а доске восемь геометрических фигур.
1![]() ) 2) 3)
) 2) 3)
![]() 4) 5)
4) 5)
 6) 7) 8)
6) 7) 8)
Вопросы:
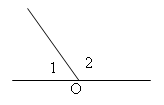
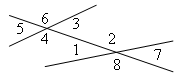
Об этой геометрической фигуре говорят, что она делит плоскость на две полуплоскости [5].
Об этой геометрической фигуре говорят, что у неё есть «дополнительный родственник» [8].
Об этом геометрическом понятие говорят как о геометрической фигуре [3].
Этой геометрическая фигура имеет длину [2].
Эта геометрическая фигура не имеет размера, но всё в геометрии связано с ней [7].
I
 I тур. Треугольники.
I тур. Треугольники.
1) 2) 3)
4
 ) 5) 6)
) 5) 6)
Вопросы:
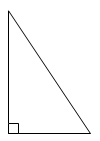
Этот треугольник имеет одну замечательную точку [2].
Сумма двух углов этого треугольника равна
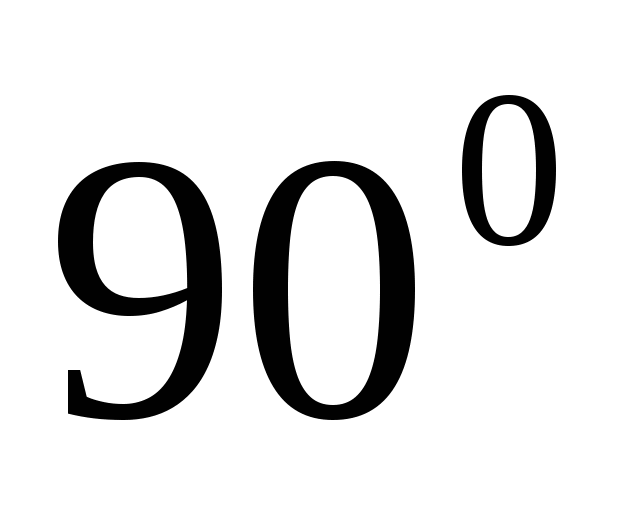 [5].
[5].Его стороны являются касательными [6].
Его площадь можно найти по формуле
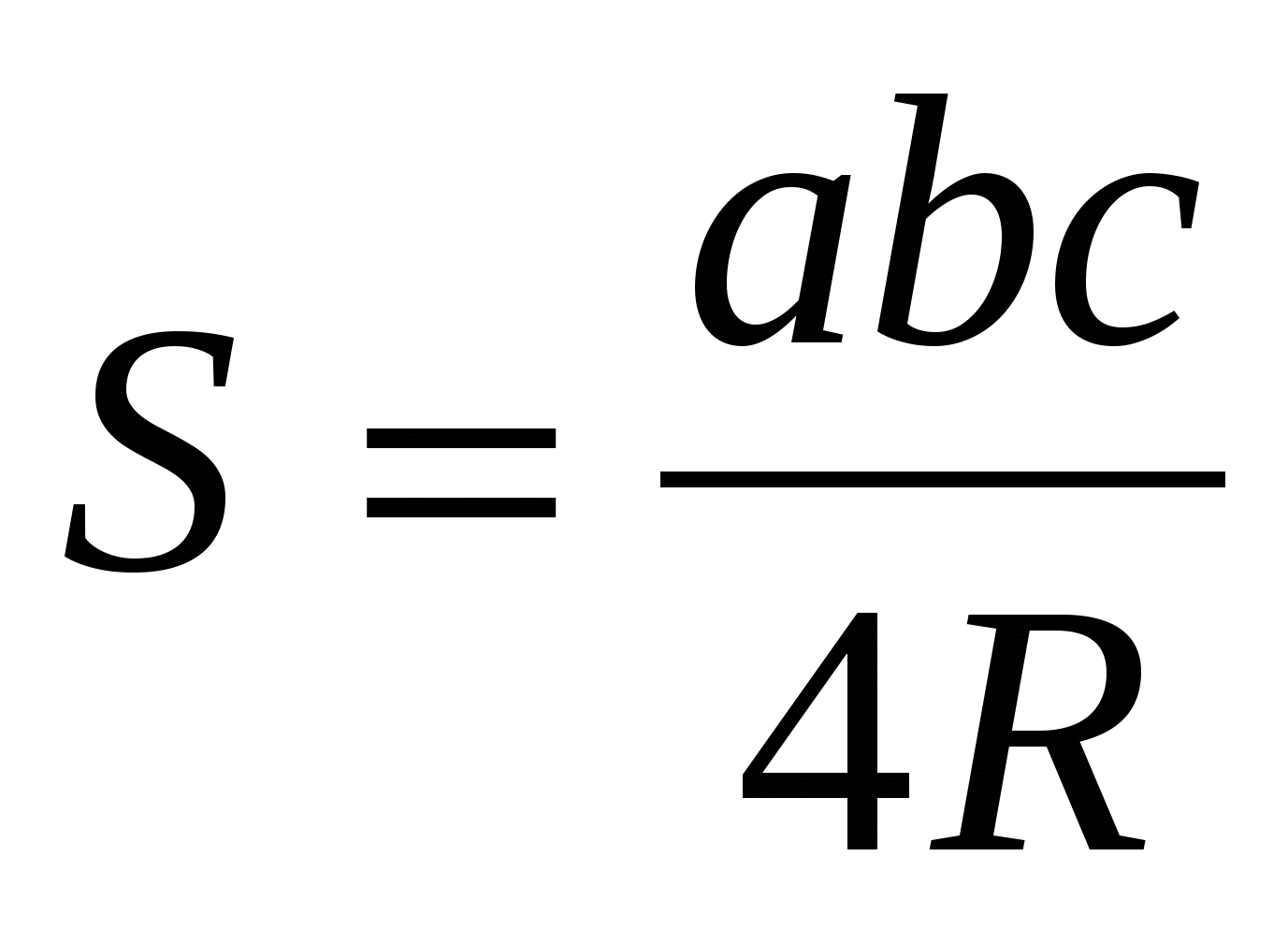 [4].
[4].В этом треугольники ученики всегда с трудом строят высоту [1].
III тур. Признаки.
В ходе изучения геометрии мы знакомились с признаками равенства треугольников, параллельности прямых и т.д.
Н
 а доске:
а доске:
1) 2)
3
 ) 4)
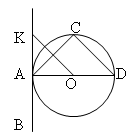
) 4) ![]() - касательная
- касательная
Докажите, что четырехугольник параллелограмм.
Докажите параллельность прямых.
Докажите равенство треугольников.
Докажите подобие треугольников.
IV тур. Площади.
На доске:
1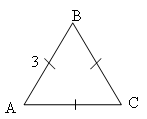
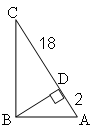
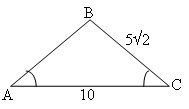 ) 2) 3)
) 2) 3)
4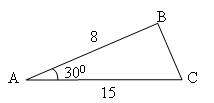
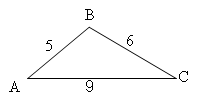 ) 5)
) 5)
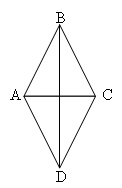
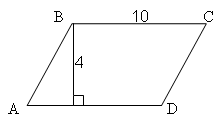
6) 7)
![]()
Ответы:
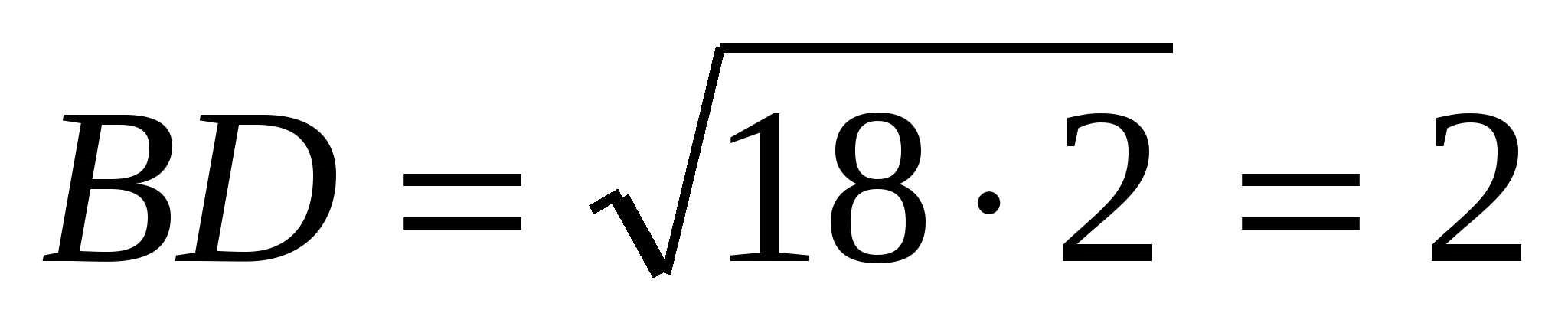 ,
, 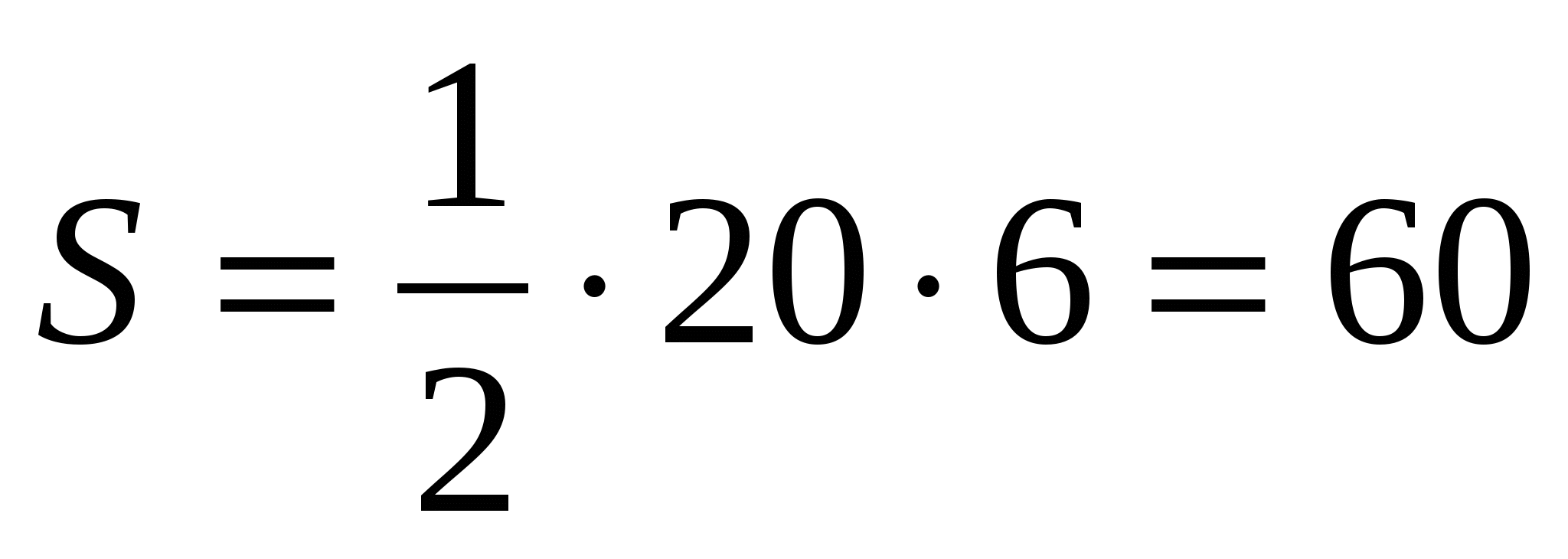 , 4)
, 4) 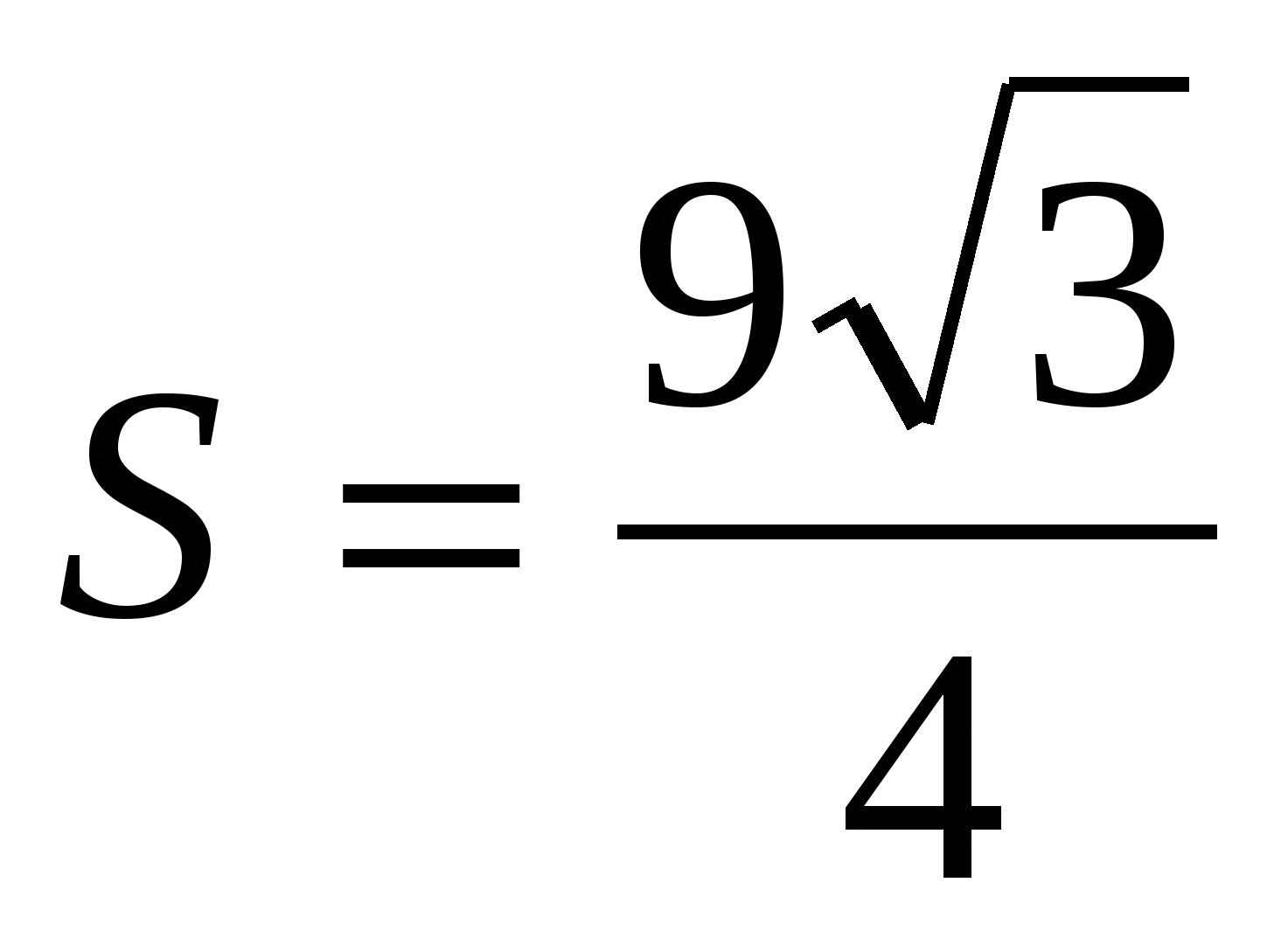
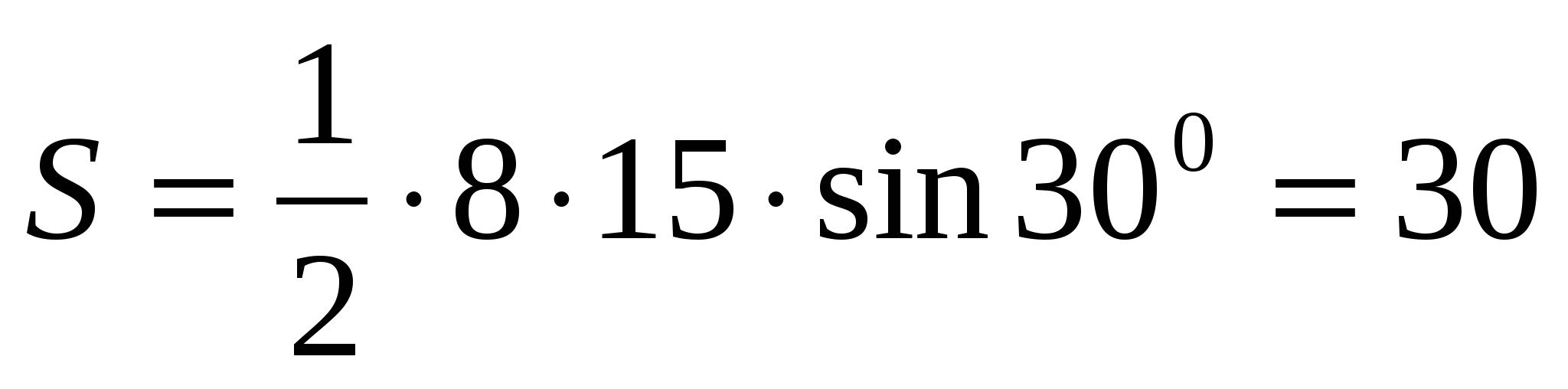 , 5)
, 5) 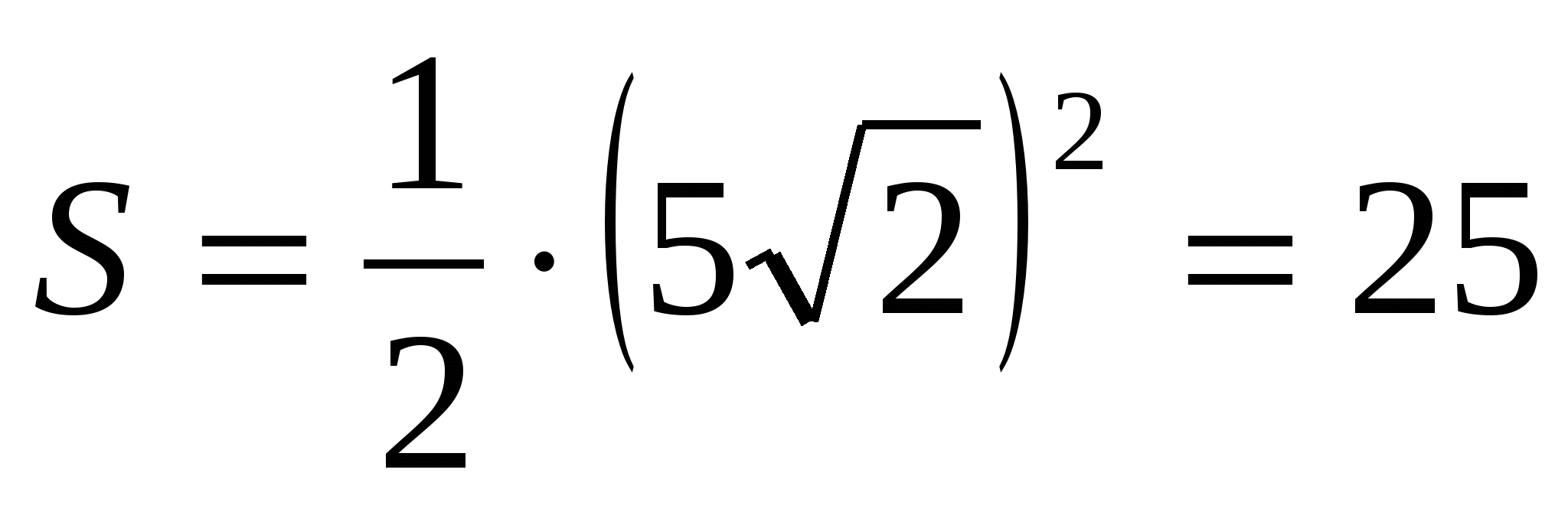
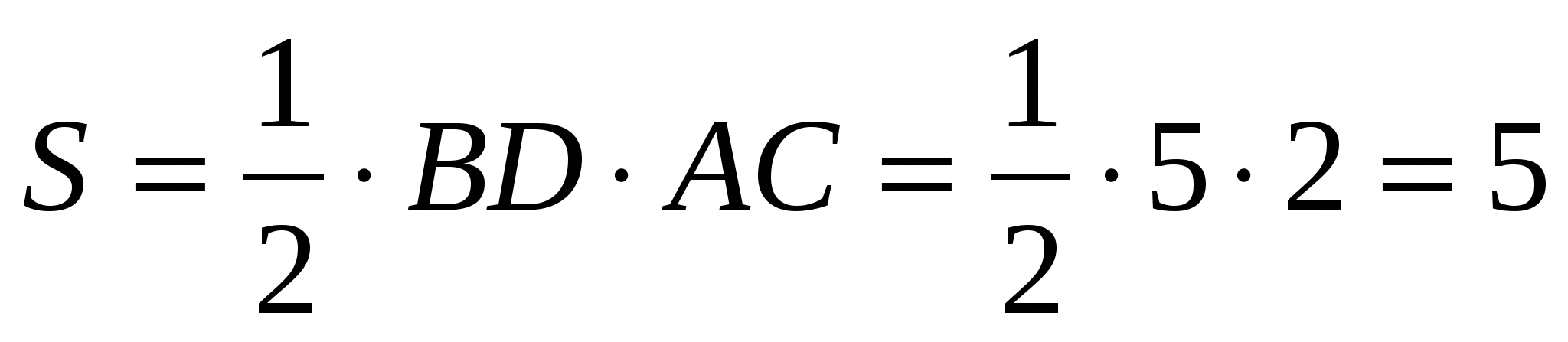 , 6)
, 6) 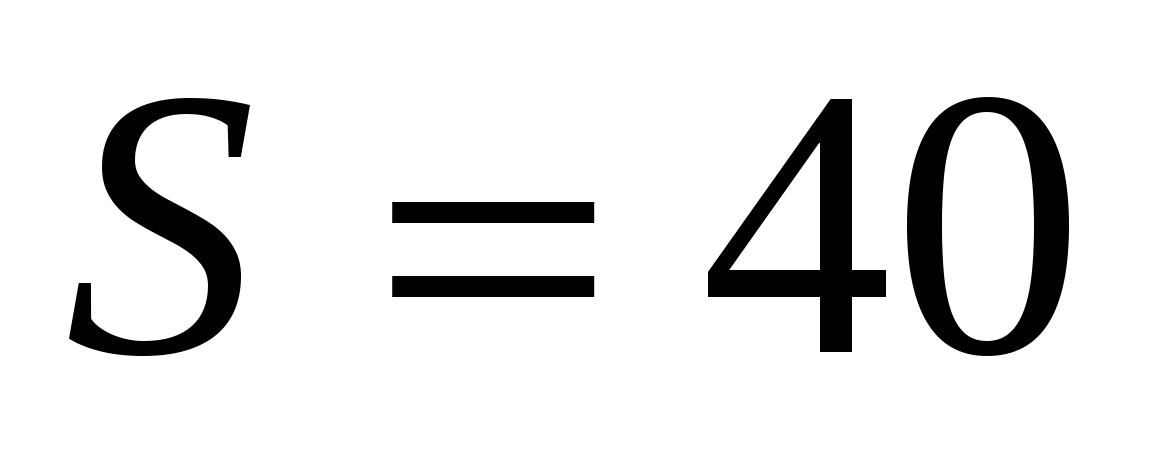
7. ![]()
Называется номер решения, участники называют номер чертежа.
V тур. Продолжите теорему.
Сумма углов треугольника …
Если параллельные прямые пересечены секущей, то …
Если в треугольнике квадрат стороны …
Средняя линия треугольника …
Точка пересечения медиан треугольника …
Вписанный угол …
Если прямая проходит через конец радиуса, лежащей на окружности, и перпендикулярна ему, то …
Если три угла одного треугольника … (должен найти ошибку).
Отношение площадей двух подобных треугольников равно …
VI тур. Дополнительный.
Решение задач (даются карточки). Остаются двое.
VII тур. Финал.
На доске плакат:
Математика – это доказательство.
Составьте как можно больше слов из слова «доказательство».
Победитель получает звезду.
Ключи от форта математики
В игре участвуют команды по 4-6 человек, которые формируются из учащихся 7-8-х классов. Игра состоит из 5 этапов.
ЭТАП 1. ПЕРЕПРАВА.
Команды выстраиваются по линии старта. По одному игроку от каждой команды выходят вперёд и получают карточку с пятью заданиями и карточки с ответами. Такие же карточки с заданиями и ответами выдаются и командам. Решив первое задание, игрок и команда по сигналу ведущего показывают карточки с ответом. Если оба ответа верные, то команда получит 2 «ключа», если верный ответ один – один «ключ», если верного ответа нет, то команда не получает ни одного «ключа». После получения «ключей» игрок делает ещё шаг вперёд и переходит ко второму заданию. После «переправы» первых игроков на старт выходят вторые, третьи и четвёртые игроки, после чего переправа заканчивается, и команды переходят ко второму этапу.
Для первого игрока.
Какое число делится без остатка на любое целое число, отличное от нуля? (0)
Найдите число,
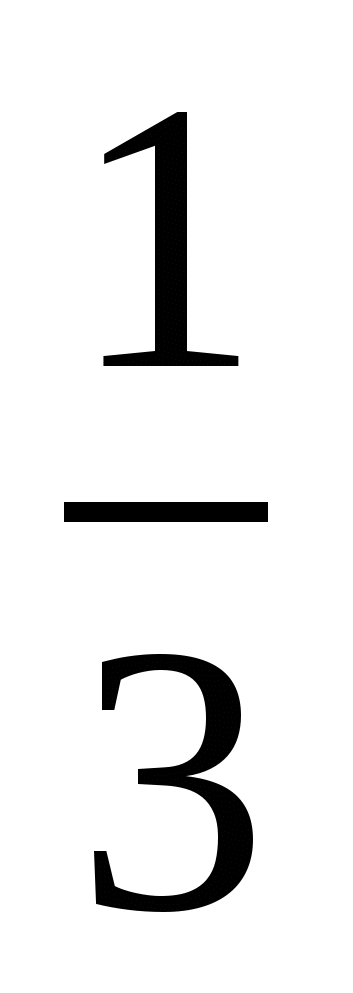 и
и 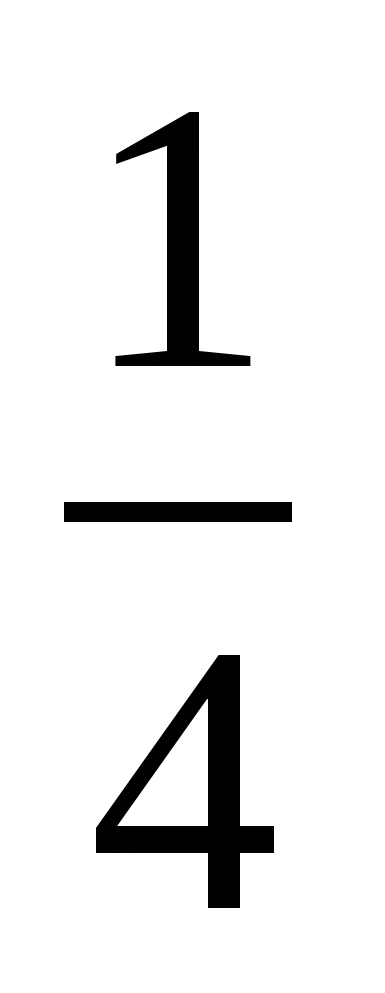 которого в сумме составляют 21. (36)
которого в сумме составляют 21. (36) Каждое из трёх натуральных чисел разделили на их сумму; полученные числа сложили. Что получилось в итоге? (1)
Чему равно частное, когда делимое и делитель равны между собой? (1)
Подряд выписаны 99 натуральных чисел 1, 2,… 99. Сколько раз в записи встречается цифра 5? (20)
Карточки с ответами: 19; 3; 20;1;36; 0.
Для второго игрока.
1. К однозначному числу приписали такую же цифру. Во сколько раз увеличилось число? (11)
2. 60 листов книги имеют толщину 1 см . Какова толщина книги, если в ней 240 страниц? (2)
3. Три курицы за 3 дня снесли три яйца. Сколько яиц снесут 12 кур за 12 дней? (48)
4.Стоимость книги 25 р. И ещё половина стоимости. Сколько стоит книга? (50)
5. Пять землекопов за 5 ч. выкапывают 5 м канавы. Сколько землекопов за 100 ч. выкопают 100 м канавы? (5)
Карточки с ответами: 4; 12; 100; 11; 2; 48;50; 5.
Для третьего игрока.
1.Бревно длиной 5м нужно распилить на метровые чурки. Каждый распил занимает 1.5мин. За сколько минут распилят бревно? (6)
2.Двое очистили 400 картофелин: один чистил 3 штуки в минуту, второй – 2; второй работал на 25 минут больше. Сколько времени
работал каждый? (70; 95 )
3. Изделие весит 89,4г. Сколько тонн весит миллион таких изделий?
(89,4)
4.Трое играли в шашки. Всего сыграно три партии. Сколько партий сыграл каждый? (2)
Карточки с ответами: 8940; 3; 80; 6; 89,4; 2; 70; 95; 7,5.
Для четвёртого игрока.
Первая женщина- математик. (Гипатия)
Математик, проживший всего 20 лет, но обессмертивший своё имя
(Галуа)
Немецкий учёный, философ и лингвист, историк и биолог, дипломат и политик, математик и изобретатель. (Лейбниц)
Русский учёный, 19 лет был ректором Казанского университета, создатель неевклидовой геометрии. (Лобачевский)
Английский математик, больше известный своими физическими законами. (Ньютон)
Ответы: Понтрягин; Декарт; Э.Галуа; Лейбниц; Лобачевский; Ньютон; Гипатия.
ЭТАП 2 «НАБОРЩИКИ»
Команды должны составить как можно больше слов из букв слова АРИФМЕТИКА. За каждое слово команда получает «ключ».
Конкурс болельщиков.
Болельщикам выдаются открытки и ножницы. Они должны прорезать в открытке отверстие, через которое могли бы пролезть сами. (Сложить открытку вдвое, сделать надрез по сгибу, не доходя до конца, затем сделать надрезы, перпендикулярные линии сгиба и краю открытки. Получившуюся ленту растянуть.)
ЭТАП 3. «С полуслова»
Участвуют по 2 человека от команды. Они получают текст с определениями, теоремами, формулами и высказываниями, один читает половину текста, второй должен закончить формулировку.
Вариант для 7- го класса.
1.Инструмент для вычерчивания окружностей -…..
2.Треугольник – фигура, состоящая из …
3.Прямые называются параллельными, если …
4.Функция вида ![]() называется …
называется …
5.Графиком линейной функций является …
6.Аксиома – это утверждение …
7.![]() - это формула …
- это формула …
8.Графиком функции ![]() и
и ![]() являются …
являются …
9.Дробь, называется правильной, если …
10. 1250 – это угол …
Вариант для 8 класса.
В прямоугольнике диагонали …
Биссектриса – это луч …
Арифметическим квадратным корнем из числа a называется …
 - …
- …Трапеция – это четырёхугольник, у которого …
Чтобы разделить отрезок на девять равных частей, нужно знать теорему …
В параллелограмме противоположные стороны …
Чтобы отложить угол 720, нужно воспользоваться …
Корень из произведения равен …
Корень из дроби равен …
Команды получают «ключ» за каждый правильный ответ.
После этого этапа подводится предварительный итог и остаются две команды, набравшие большее количество «ключей».
ЭТАП 4. «АУКЦИОН»
Команды по очереди называют математические термины, содержащие, например, букву «п». Команда, которая не смогла слово, проигрывает. Победившая команда получает «ключ».
ЭТАП 5. «ДА ИЛИ НЕТ»
Участвуют по одному представителю от команды (обычно это капитаны). Ведущий поочерёдно задаёт вопросы в форме «Верно ли, что …» представителям команд, которые отвечают на них «да», если согласен, и «нет», если не согласен.
Вариант для 7 класса.
1.Через любые две точки можно провести прямую. (Да)
2.Если две прямые имеют общую точку, то они пересекаются. (Нет, могут совпасть.)
3.Две пересекающие прямые имеют только одну общую точку. (Да)
4.Точки, ограничивающие отрезок, называются его концами. (Да)
5.Графиком линейной функции является прямая. (Да)
6.График функции y=3x+5 проходит через начало координат. (Да)
7.Часть прямой, ограниченная двумя точками, - луч. (Нет)
8.Если два угла равны, то они вертикальные. (Нет)
9.Точка, делящая отрезок пополам, называется его серединой. (Да)
10.Чтобы построить график функции, достаточно двух точек. (Нет)
11.Если два угла имеют общую вершину, то они смежные. (Нет)
Вариант для 8 класса.
1.Если четырёхугольник- параллелограмм, то его противоположные стороны равны. (Да)
2.Если диагонали четырёхугольника точкой пересечения делятся пополам, то это- параллелограмм. (Да)
3.Если в параллелограмме один из углов равен 600, то другой равен 1300. (Нет)
4.Углы при основании равнобедренной трапеции равны. (Да)
5 .Если средняя линяя треугольника равна 4см, то параллельная ей сторона равна 2см. (Нет)
6.Если четырёхугольник – ромб, то его противоположные углы равны. (Да)
7.Диагонали параллелограмма равны. (Нет)
8.![]() =6. (Нет)
=6. (Нет)
9.Трапеция в переводе с греческого – «столик».
10.Фалес доказал теорему о сумме углов треугольника. (Нет)
11.Катет, лежащий против угла в 300, равен половине гипотенузы. (Да)
Производится подсчёт «ключей». Победившая команда получает большой ключ от форта Математика.
ЛИТЕРАТУРА
1.Журнал «Математика в школе» 2006г. №7, №9; 2004г. №9.
2.Устный счёт./ Сост. П.М.Камаев,- М.,- Чистые пруды, 2007г. - ( Библиотечка «Первое сентября», серия «Математика», Вып. 3(15)).
3.Газета «Математика». Приложение к газете «Первое сентября». 2003г.№45, 2007г.№13, 2008г, №16.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ