Внеклассное мероприятие по математике «Путешествие в царство прогрессий»
МБОУ «Ивановская средняя общеобразовательная школа»
по математике
«Путешествие в царство прогрессий»
Разработала учитель математики
Минаева И.И.
2014
Тема: «Путешествие в царство прогрессий»
Цель: Рассмотреть некоторые исторические сведения, связанные с арифметической и геометрической прогрессиями. Повторить основные понятия арифметической и геометрической прогрессий, закрепить навыки в решении задач
Оборудование и оформление: Таблицы нумераций разных народов, таблицы к конкурсу «Угадайка!», рисунки с условиями задач и заданий к ним, кубы для лабиринта – викторины, входные талоны и контрольные карточки к ним.
План:
1 этап - конкурс «Угадайка».
2 этап - консультация.
3 этап - лабиринт-викторина.
Правила игры
1. Класс разбивается на две команды.
2. Выбираются капитаны команд.
3. Капитаны команд назначают консультантов. Они должны помогать школьникам другой команды отвечать на вопросы.
4. После слов «Консультация окончена» школьники занимают свои места. В противном случае команда наказывается штрафными очками.
5. Для участия во всех видах работы ученики вызываются к доске капитанами команд.
- Ребята, сегодня мы совершим путешествие в «царство арифметической и геометрической прогрессий». Вспомним с вами основные понятия арифметической и геометрической прогрессий и закрепим навыки в решении задач по этой теме.
Но прежде сделаем разминку, т.е. проведем конкурс «Угадайка!», а заодно и проверим ваши вычислительные навыки.
Этот конкурс состоит из двух заданий. Для выполнения первого задания мне надо по одному участнику из каждой команды. (Даю им карточки и они работают с таблицами нумераций разных народов).
Карл Фридрих Гаусс родился в MDCCLXXVII году. Прочитайте год рождения Гаусса. Архимед прожил ѻє лет. Прочитайте, сколько лет он жил?
ѻє - 75 MDCCLXXVII - 1777
Второе задание выполняет вся команда.
Задание 1-ой команде.
Узнайте по описанию, о ком идет речь: Известный математик и механик древности. Родился в г. Сиракузы на о. Сицилия . Будучи на службе у царя Гиерона II, при помощи найденного им закона выталкивающей силы, определил чистоту состава золотого венца царя Гиерона II.
Крылатыми стали его слова: «Дайте мне точку опоры, и я поверну Землю».
Огромен вклад ученого и в развитие математики. Им найдены площади эллипса, поверхности конуса и шара, объемы шара и сферического сегмента. Ученый вычислил отношение длины окружности к диаметру (число π). Он нашел также сумму бесконечной геометрической прогрессии со знаменателем ¼. В математике это был первый пример бесконечного ряда. Если вы уже догадались, кто это, то проверьте себя.
Ответ каждого примера замените буквой, букву запишите в «окошечко» лабиринта. Прочитайте.
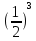 ∙ 16
∙ 16
Р
-4,2∙ 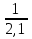 +7
+7
И
-5+1,885
Х
0,53 ∙ 8
М
(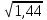 +0,3) ∙ 4
+0,3) ∙ 4
А
10 ∙ 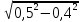
Е
7,7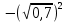
Д
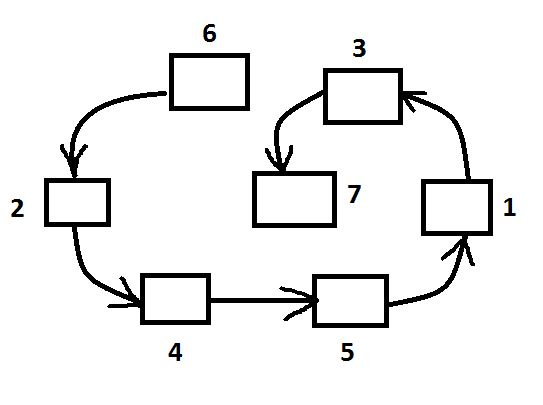
Задание 2-ой команде.
Немецкий математик, астроном, физик. Решил проблему, связанную с построением правильных многоугольников с помощью циркуля и линейки. Этого момента девятнадцатилетний юноша окончательно решил заниматься математикой. Его многочисленные исследования в области алгебры, теории чисел, геометрии и математического анализа оказали серьезное влияние на развитие теоретической и прикладной математики, физики, астрономии.
С формулой суммы первых n – членов арифметической прогрессии связан интересный эпизод из жизни этого математика. Когда ему было 9 лет, учитель, занятый проверкой тетрадей учеников других классов, задал на уроке следующую задачу: сосчитать сумму всех натуральных чисел от 1 до 40 включительно. Каково же было удивление учителя, когда один из учеников (это был математик, о котором идет речь) через минуту воскликнул: «Я уже решил!».
Большинство учеников после долгих подсчетов получили неверный результат. В тетради же этого ученика было только одно число, но зато верное.
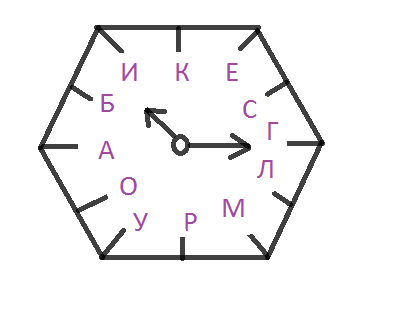
₂
(
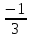 ) * (-108)
) * (-108)
5 ₃
(
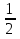 ) * 4
) * 4
-1,5 *6 +15
10*
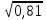
₃
0,007 * 10
₂
(1,2 - 1,41) *100
1
4
3
5
7
4
6
2
2
Если вы уже догадались, кто это, то проверьте себя. Решите примеры и под номером примера в «окошечко» вместо ответа запишите букву соответствующую этому числу. Номера примеров повторяются, значит под ними будут стоять одинаковые буквы.
Удачи вам в этом конкурсе!
Жюри подводит итоги.
Следующий этап нашей игры – консультация. На консультацию отводится 10-12 минут. В командах назначаются консультанты. Они должны помогать школьникам из другой команды отвечать на вопросы. Их работа приносит дополнительные очки своей команде. Отказ от проведения консультации наказывается очками в пользу команды противника.
Разрешаются и взаимоконсультации.
На доске открываются заранее подготовленные вопросы и задания, которые необходимо выполнить.
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
ГЕОМЕТРИЧЕСКАЯ ПРГОГРЕССИЯ
Дайте определение арифметической прогрессии
Дайте определение геометрической прогрессии
Запишите формулы:
а) n-го члена арифметической прогрессии;
б) суммы n-первых членов арифметической прогрессии.
Запишите формулы:
а) n-го члена геометрической прогрессии;
б) суммы n первых членов геометрической прогресии.
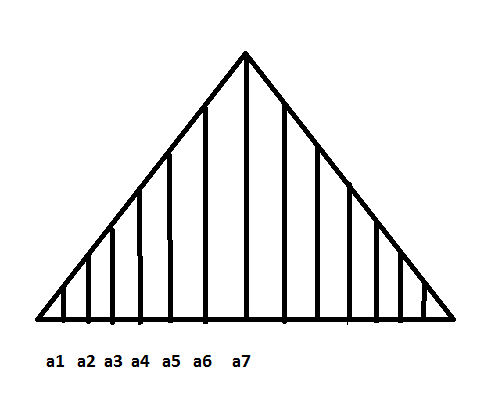
Задача: вертикальные стержни фермы имеют такую длину: наименьший а=5 дм, а каждый следующий на 2 дм длиннее. Записать длину семи стержней.
Задача: В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две. Записать колонию, рожденную одной бактерией за 7 минут
Запишите последовательность в соответствии с условиями задачи.
Запишите последовательность в соответствии с условием задачи.
Найдите разность d между предыдущим и последующим членами последовательности.
Найдите частное q от деления последующего члена последовательности на предыдущий.
Задайте последовательность рекуррентным способом; формулой n-ого члена последовательности
Задайте последовательность рекуррентным способом; формулой n-ого члена последовательности; формулой
Сначала школьники проделывают всю работу на доске и в тетрадях для арифметической прогрессии, а потом для геометрической. Учитель предлагает вопрос, а капитаны команд называют для ответов учащихся из других команд по очереди.
Заключительный этап игры – лабиринт –викторина. Викторина проводится так. Каждый член команды проходит лабиринт самостоятельно, получив входной талон в лабиринт, на котором написано число (например, 50). Получив талон, находит куб, на одной из граней которого написано это число, и выполняет указанное там задание (найти 20% от этого числа). Результат действия (ответ задачи) он должен найти на другой грани куба и снова выполнить написанное задание и т.д.
После решения всех заданий на кубе ученик подходит к контрольному пункту и сообщает ответ. Если цепочка заданий выполнена правильно, без ошибок, то ответ совпадает с контрольным числом, и ученик считается прошедшим лабиринт.
Прошедшие лабиринт могут помочь своим товарищам.
Команда прошла лабиринт, если все ее члены прошли свои лабиринты. При этом каждый участник, сумевший пройти куб, приносит команде 1 очко.
Подводятся итоги соревнования и называется команда –победитель.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ