Соснина Галина Кузьминична

Учитель математики

МБОУ «СОШ№2» г. Мегион

Дифференцированное обучение

на уроках математики,

в разноуровневом классе,

как личностно-ориентированный подход к процессу обучения и воспитания.

Выполнила:

Соснина Г.К., учитель математики

I квалификационной категории

г. Мегион

2012 г.

Цель: Выработать ряд методических путей для осуществления дифференциро­ванного обучения учащихся на уроках математики, обеспечивающих возмож­ность каждому ребенку развивать свои способности, самостоятельно приобре­тать новые знания, развивать их интеллектуальную и нравственную культуру.

Задачи:

1. Изучить и проанализировать психолого-педагогическую литературу по теме исследования.

2. Выработать оптимальные методы, приемы и формы работы, позволяю­щие каждому ребенку развивать свои способности в зоне ближайшего развития.

3. Проверить на практике целесообразность и эффективность разработан­ных технологий по дифференцированному обучению на уроках матема­тики.

Объект исследования: учащиеся 6 класса, изучающие математику по общеоб­разовательному курсу.

Предмет исследования: проблема теории дифференцированного обучения, а также изучение способов дифференцированного обучения на уроках математики.

I. Введение (Мотивационный и целевой компонент).

Проблема дифференцированного подхода не является новой для наших школ. Однако выдвижение и развитие концептуальной идеи планирования обя­зательных результатов обучения позволило подойти к этой проблеме с новых позиций.

Принципиальное отличие нового подхода состоит в том, что перед разны­ми категориями учащихся ставятся различные цели: одни ученики должны дос­тичь определенного объективно обусловленного уровня математической подго­товки, называемого базовым, а другие, проявляющие интерес к математике и обладающими хорошими математическими способностями, должны добиться более высоких результатов.

Педагогикой и психологией установлено, что по своим природным спо­собностям, уровню восприятия, темпу работы, а главное по специфике мысли­тельной деятельности учащиеся сильно отличаются друг от друга.

В одном классе можно наблюдать школьников с крайними противополож­ными друг другу уровнями развития (от высокого до низкого).

В данной ситуации учитель вынужден выбирать формы и методы обуче­ния, направленные на достижения результатов средними учениками. Но при этом слабым ученикам уделяется недостаточное внимание, а сильные и талант­ливые ребята и вовсе выпадают из поля зрения учителя.

При таком отношении сильные ученики теряют интерес к учению, им ста­новиться скучно на уроках, и в результате к концу обучения талантливые дети превращаются в посредственных учеников.

Что же касается слабых учеников, то задания среднего уровня кажутся им непосильными. Появляется ощущение неполноценности, боязнь высказывать свои суждения при ответах. Из-за этого такие ученики, в конце концов отказы­ваются от какой-либо мыслительной деятельности, используя обходные пути: механическое заучивание, ожидание подсказок, списывания. В конце концов, у слабых учащихся возникает отвращение к учению.

Все эти негативные явления можно преодолеть, организуя дифференциро­ванию работу внутри класса. Т.е. используя внутреннюю дифференциацию.

Тема: «Дифференцированное обучение на уроках математики, в разно­уровневом классе, как личностно-ориентированный подход к процессу обуче­ния и воспитания», актуальна в настоящее время.

Поэтому для меня, как учителя, стоит задача: выработать ряд методиче­ских путей для осуществления дифференцированного обучения учащихся на уроках математики, обеспечивающих возможность каждому ребенку развивать свои способности, самостоятельно приобретать новые знания, развивать их ин­теллектуальную и нравственную культуру.

В своей педагогической деятельности я определила для себя первоочеред­ные задачи:

1. Изучить и проанализировать психолого-педагогическую литературу по теме исследования.

2. Выработать оптимальные методы, приемы и формы работы, позволяю­щие каждому ребенку развивать свои способности в зоне ближайшего развития.

3. Проверить на практике целесообразность и эффективность разработан­ных технологий по дифференцированному обучению на уроках матема­тики в разноуровневом классе.

II. Основная часть (Содержательный компонент). Чтобы выработать ряд методических путей для осуществления дифферен­цированного обучения учащихся на уроках математики, обеспечивающий воз­можность каждому ребенку развивать свои способности, самостоятельно при­обретать новые знания, развивать их интеллектуальную и нравственную куль­туру. Я использовала в максимальной мере опыт традиционной дидактики, а также современные методические разработки и журнала «Математика в школе» за разные годы издания.

Реальностью, обуславливающей необходимость дифференцированного обучения являются объективно существующие различия учащихся в темпах ов­ладения учебным материалом, а также самостоятельном применении усвоен­ных знаний на основе психологической диагностики учащихся и проведения срезовых работ и последующих наблюдений.

По отмеченным признакам учащиеся условно могут быть разделены на 3 группы.

/ группа - учащиеся с высоким темпом продвижения в обучении: общие схемы выполнения типовых задач усваивают в процессе первич­ного объяснения, во многих случаях могут самостоятельно нахо­дить решения измененных типовых или усложненных задач; предполагающих применение нескольких известных способов решения.

II группа - учащиеся со средним темпом продвижения в обучении: овладе-

ние новыми знаниями и умениями не вызывает особых затрудне­ний, способы выполнения типовых заданий усваивают после рас­смотрения образцов, решения измененных и усложненных задач находят, опираясь на указания учителя.

III группа - учащиеся с низким темпом продвижения: при усвоении нового

материала испытывают определенные затруднения, во многих случаях нуждаются в дополнительных разъяснениях, обязатель­ными результатами овладевают после достаточно длительной

тренировки, способности к самостоятельному нахождению реше­ний измененных и усложненных задач, как правило, не проявля­ют.

В каждом классе, где я работаю, присутствуют дети из всех условно раз­деленных групп.

Как организовать обучение?

Как обеспечить достижение учащимися обязательных результатов и при этом создать условия для усвоения изучаемого материала на более высоких уровнях учащимися, проявляющими интерес и способности к математике?

В течение 3 лет, но 7 лет назад, я занималась проблемой «Дифференциро­ванного обучения в разноуровневом классе».

В моей практике сложилась определенная система обучения математике на основе обязательных результатов - «Зачетная система».

Огромную помощь оказали курсы в Ханты-Мансийске, на которых читали свои лекции московские ученые Н.А. Лурье и С.С. Минаева, статьи в журнале «Математика в школе».

Тематические зачеты, которые я провожу, представляют одну из возмож­ных форм осуществления контроля за усвоением материала в условиях уровне-вой дифференциации, главная особенность которой состоит в дифференциации требований к знаниям и умениям учащихся. По каждой теме выделен уровень обязательной подготовки который, задает достаточную нижнюю границу ус­воения материала.

При нормальном процессе обучения этот уровень доступен школьникам и его достижение считается явным успехом, на его основе формируются повы­шенные уровни усвоения материала.

Достижению поставленной цели способствует двухступенчатая структура зачетной работы, составленной соответственно из двух частей: обязательной и дополнительной. Первая из них нацелена на проверку достижения обязательно­го уровня усвоения конкретной темы. Эта часть и составляет собственно со­держание тематического зачета и по ее выполнению определяется, сдал (достиг обязательного уровня овладения темой) или не сдал учащийся зачет. Вторая

часть направлена на проверку овладения темой на повышенном уровне и ее вы­полнение позволяет ученику получить дополнительно одну из оценок «4» или «5».

Выполнение дополнительной части оценивается только в том случае, если ученик показал хорошее овладение обязательным материалом. Зачеты я прово­жу открытые и закрытые.

Перед началом изучения темы вывешивается список обязательных резуль­татов (составляю сама аналогичные задачи). Это позволяет наглядно продемон­стрировать учащимся предъявляемые требования, открытость этих требований, их доступность оказывают стимулирующее воздействие на учащихся.

«Закрытый зачет», на мой взгляд, менее эффективен, т.к. дети не могут определится в выборе конечного результата до зачетного урока.

В собственном журнале выделяю две графы. В одной результаты обяза­тельной части, в другой дополнительной. Для фиксации результатов обязатель­ной части использую таблицу:

Ф.И. ученика

Зачет № _ по теме: « ___________»

Обязательная часть

Дополнитель­но

1

2

3

4

5

6

7

8

9

10

1 1

1

2

1

3

На основе этой таблицы можно организовать целенаправленную работу со всем классом, а также индивидуальную работу с каждым учеником по выпол­нению обнаруженных пробелов.

Для этого у меня по каждой теме и контрольному заданию составлены карточки с заданиями - индивидуальные задания для устранения ошибок.

Учителю удобно планировать дальнейшую работу после занесения резуль­татов в таблицу. Если в столбце много минусов, стоит задуматься над методи­кой объяснения того или иного материала и над формами работы при закрепле­нии.

Повторение для сдачи зачета организую, включая упражнения в решении устных задач, предлагаю решать задачи по образцу, домашние, тренировочные упражнения и, наконец индивидуальные консультации. После достаточной тре­нировки приходит время повторить сдачу зачета, не все отставшие делают это одновременно. Иногда ученик получает зачетное задание у доски, как дополне­ние к ответу по новой теме, иногда карточки на перемене, иногда на индивиду­альной консультации, т.е. в любой удобный случай.

Почти все учащиеся заинтересованы сдать зачет своевременно. Причины сильных пробелов в подготовке учеников кроются в недостаточной отработке навыков. И очень много времени тратиться на изготовление карточек с зада­ниями, на составление задач разных уровней сложности.

Во всем остальном, я думаю, это система дает только положительный ре­зультат. Несмотря на всё трудности, считаю её эффективной способствующей повышению качества обучения.

Перед слабыми учениками зачет ставит посильную для него цель, сильных подстраховывает, защищая перед пренебрежением элементарными навыками.

Многие довольно быстро овладевают материалом на уроке обязательной подготовки, поэтому появляется реальная возможность предлагать им более сложные задания разного уровня сложности.

Уровень усвоения я проверяю самостоятельными проверочными работами на 5-7 минут после первичного закрепления нового материала. Вторичное за­крепление у меня уже дифференцированно.

При организации дифференцированного обучения в разноуровневом клас­се, класс разбиваю на 3 группы по результатам успеваемости, отношению к де­лу. Это разбиение будет стабильно в течение года, хотя частные переходы из группы в группу возможны.

Итак, I группа - с высокими учебными возможностями, II группа - со средними учебными возможностями, III группа - с низкими учебными возмож­ностями.

Дифференцированный подход целесообразно осуществлять на определен­ных этапах урока. Так на этапе формирования новых знаний необходимо рабо-

тать со всем классом без деления на группы. После того как учитель объяснит всему классу новый материал и проведет первоначальные формирования уме­ний по данной теме, следует переходить к закреплению умений, доведению их до навыков.

Именно здесь можно использовать задания различной сложности. Эти за­дания различаются не только содержанием, но и формой их подачи.

Задания я составляю в двух вариантах:

I вариант - для группы учащихся с высокими учебными возможностями.

II вариант - предназначен для группы учащихся со средними и низкими
учебными возможностями.

Вариант II содержит большое количество простых тренировочных упраж­нений с постепенным пошаговым нарастанием трудности в I варианте преобла­дают задания комбинированного характера, требующие установления связей между отдельными компонентами курса и применения нестандартных приемов решения. В каждом варианте упражнения начинаются с простейших и распола­гаются по возрастающей сложности. Однако это возрастание в разных вариан­тах проходит с разным ускорением.

Вариант II строится таким образом, что переход от одного упражнения к другому связан с небольшим варьированием данных или с незначительными усложнениями формулировки задания. Такой подход позволяет решить важную дидактическую задачу предоставить слабым учащимся возможность на каждом шаге преодолевать только одну какую-либо трудность.

В I сложность заданий возрастает в значительно более высоком темпе. Это позволяет быстрее пройти начальный этап формирования соответствующего умения и выйти на усложненные, комбинированные задания.

В качестве примера рассмотрим систему упражнений для самостоятельной работы по темам:

• сложение и вычитание обыкновенных дробей с разными знаменателями;

• умножение обыкновенных дробей;

• деление обыкновенных дробей. (смотри Приложение 1).

В каждый вариант наряду с тренировочными задачами я включаю задачи развивающего характера, решение которых связано с проявлением смекалки, сообразительности.

Многие исследователи отмечают, что отставание слабых учащихся по ма­тематике связано с низким уровнем их развития.

Поэтому считаю, что не только сильным, но и слабым учащимся надо предлагать задания, требующие нестандартных решений.

Задания тренировочного характера, (смотри Приложение 2).

В каждом из вариантов я предусматриваю инструктивный материал, пред­назначенный для оказания учащимся помощи в выполнении предлагаемых за­даний.

Особенность II варианта состоит в том, что в нем инструктивный материал представлен достаточно широко. Это образцы решений, алгоритмического предписания, задания с начатым, но не оконченным решением, задания с про­пущенными данными, задания с выбором ответа, данные для самоконтроля, от­веты.

Задания, содержащие инструктивный материал, (смотри Приложение 3).

Описанная система дифференцированных заданий была мной апробирова­на 7 лет назад. Я хочу отметить, что разноуровневые задания облегчают орга­низацию занятий в классе, создают условия для продвижения школьников в учебе в соответствии с их возможностями. Но в тоже время требуют больших затрат времени и сил учителя (составление разноуровневых заданий).

Практика показала, что слабые учащиеся охотно выполняют задания со­держащие инструктивный материал особенно те упражнения в которых приве­дены данные для самоконтроля. Это позволило сделать вывод, что таким школьникам недостаточно только показать ответ (как это делается в учебнике). Выяснив, что получен неверный ответ к заданию, ученик не в состоянии про­следить всю цепочку и найти ошибку.

Формы подачи данных заданий:

а. II - III группы решают общее задание фронтально под наблюдением
учителя, а I группа выполняет общее или индивидуальное задание самостоя­
тельно. Для них предусмотрен какой-либо вариант проверки с использованием
поворотной доски, магнитной доски, с обратной стороны доски.

б. I группа вместе с учителем разбирают задания повышенной сложности,
а II и III работают самостоятельно.

в. Учащиеся II, III группы работают самостоятельно, I группа получает
более трудное задание, III группа - более простое. Для каждой группы предназначен свой способ проверки.

В III группе работа на любом этапе идет под постоянным руководством учителя и непосредственно при полном его контроле. Используются в основ­ном, фронтальные формы объяснения нового материала. Большое значение приобретает наглядность.

Широко используется метод комментирования, когда ученик с места пояс­няет решения, учитель записывает выкладки. На доске, а учащиеся слушают, смотрят, пишут. Таким образом, включаются все виды памяти - зрительная, слуховая и моторная, увеличивается доля разговорной речи на уроке.

Индивидуальные формы работы в этих группах применимо лишь при за­креплении. Задания для самостоятельного выполнения обычно снабжаю руко­водством к действию.

Особенно часто применяю следующие виды учебных заданий:

1. Самостоятельная работа с предварительным разбором;

2. Решение задач с последующей проверке;

3. Математические диктанты с самопроверкой или взаимопроверкой;

4. Операции по заданному алгоритму;

5. Задания с готовыми ответами;

6. Тесты - невелики по объему и обязательно сопровождаются проверкой в классе.

Имеет свою специфику и работа с книгой. Она происходит в основном в виде ответов на вопросы, дословно повторяющих соответствующие - учебные тексты. Ученику предстоит только отыскать в тексте нужное слово или слово­сочетание и заполнить им пропуск в задании. Постепенно задание усложняется: нужное предложение стоит теперь не в начале, а в середине или в конце разде­ла. Затем предлагается заполнить пропуски в таком предложении, где последо­вательность слов не соответствует предложению из учебника. Применяются и такие задания, в которых требуется найти в тексте какие-то термины, формули­ровки понятий или важные числовые данные.

В III группе часто используется обсуждение материала в парах постоянно­го состава, что позволяет учащимся "раскрыться", оценить свои знания, нау­читься задавать вопросы, усовершенствовать свою речь.

Для развития интереса к учению необходимо планировать ситуацию успе­ха; предлагать домашние контрольные работы, проводить экскурсии, устраи­вать зачеты с использованием в качестве консультантов ребят из III группы. Эти приемы облегчают учебу и вместе с тем позволяют показать учащимся примеры, достойные подражания.

Для активизации учебного процесса и мотивации учения мы широко при­меняем рейтинговую оценку знаний учащихся.

Во второй группе учитель комбинирует различные формы деятельности. При усвоении новых знаний учащиеся действуют под доминирующим влияни­ем учителя. Вместе с тем происходит постепенный переход к самостоятельному выполнению заданий в знакомой и измененной ситуации. Используются твор­ческие задания, которые предполагают фронтальную работу: ответы на про­блемные вопросы, формирование вопросов по прочитанному, приведение при­меров, иллюстрирующих теоретический вопрос, составление заданий и упраж­нений. Создаются условия для сотрудничества, обсуждения проблем в парах постоянного состава.

При работе с книгой могут быть предложены такие задания:

- найти определения, дословно приведенные в учебнике (необходимо от­личать определение от простого описания понятий);

• выделить в тексте основную мысль;

• составить план прочитанного.

В качестве самостоятельных работ используются многовариантные зада­ния с готовыми ответами по типу перфокарт, а также различные виды тестов.

Для развития интереса к учению предлагаются практические работы в ка­честве домашнего задания, а также темы для подготовки докладов.

Систематически проводятся зачеты, на которых основными проверяющи­ми выступают не только ребята из I группы, но и лучшие ученики II группы.

I группе основной акцент делается на самостоятельность учащихся. При изучении и первичном закреплении новых знаний используются такие формы учебных занятий, как лекция, лабораторная работа, экскурсия, семинар.

Комплексное применение знаний и способов действий часто осуществля­ется на семинарах, а также при выполнении бригадных или индивидуальных творческих заданий.

Проверку, оценка и коррекция знаний проводятся в форме разноуровневых контрольных работ, тестов, зачетов, семинаров, конференций, общественных смотров. Учащимся часто предлагаются подборки заданий творческого харак­тера, учитывающие их познавательные интересы. Поощряется опережающая учебная работа школьников, самостоятельное добывание ими новых знаний. Домашние задания также часто рассчитаны на опережающее обучение.

При работе с учебником учитель нацеливает школьников на составление плана по прочитанному, на сравнение проработанного материала с ранее изу­ченным, на разработку сравнительных таблиц, диаграмм, схем; на составление конспекта, в котором не только кратко повторяется материал учебника, но и приводятся новые сведения из энциклопедий и справочников.

Вся деятельность учителя в I группе направлена на формирование коллек­тива, заинтересованного в углубленном изучении предмета.

В своей работе я также использую разные формы обучения:

1. парную;

2. звеньевую;

3. индивидуализированную;

4. индивидуальную.

На основе выделенных групп в классе создаются рабочие звенья, позво­ляющие учителю осуществлять дифференцированный подход и своевременную помощь каждой группе на различных этапах урока.

Практика показала необходимость выделения звеньев из 2-х, трех, четырех учащихся.

Работа со звеньями учащихся позволяет учителю сочетать на уроке груп­повую работу с фронтальной, коллективной и индивидуальной. Это, в свою очередь, способствует организации активной познавательной деятельности ка­ждого учащегося.

Состав звена комплектуется из школьников, входящих в разные типологи­ческие группы. Для удобства работы учащихся надо рассадить так, чтобы на соседних партах сидели представители разных типологических групп. В полное звено (т.е. звено, состоящее из четырех человек) включаются по одному учени­ку от каждой типологической группы или по два от наиболее многочисленных групп. При этом необходимо учитывать интересы учащихся к предмету, моти­вы учения собранность, поведение на уроке, отношение друг к другу. Не следу­ет включать в одно звено несколько недисциплинированных или имеющих от­рицательное отношение к учебе школьников. Один из членов звена назначается звеньевым, обычно это хорошо успевающий ученик. Он следит за работой зве­на, распределяет вместе с учителем задания, помогает своим товарищам.

Обязательным требованием к групповой работе в звене является выполне­ние задания каждым учеником, при этом все звенья чаще всего выполняют одинаковые задания. Практика показала, что такая работа эффективна на этапе овладения знаниями, умениями и навыками в сходных ситуациях (10-12 ми­нут); при проверке выполнения классного или домашнего задания (3—5 мин); во время опроса (5-7 мин); при выполнении устных упражнений (3-5 минут).

Покажем, как учитель математики может организовать звенья для решения конкретных задач урока. Обозначим буквами а, Ь, с и d учащихся, принадлежа­щих соответственно группам А, В, С и D.

Прежде всего, необходимо составить полные звенья. На схеме 1 представ­лен способ составления звеньев, состоящих из четырех школьников, принадле­жащих разным типологическим группам.

Из полного звена образуются звенья из двух учеников, при этом возможны три различных способа (схема 2).

СХЕМА Т . N СХЕМА 2

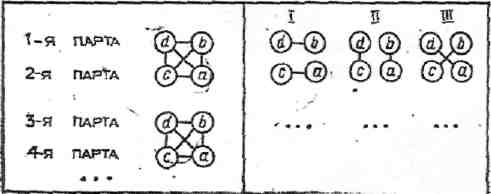
При составлении звеньев из трех учащихся возможны шесть различных способов (схема 3): в I и II случаях весь класс разбивается на звенья-тройки, а в III—VI случаях кроме учеников, включенных в звенья-тройки, в классе остают­ся учащиеся одной типологической группы, не включенные ни в одно звено. Таким образом, учитель на уроке может организовать работу с определенной типологической группой в то время, когда остальные учащиеся работают в звеньях-тройках.

»■—»■■ ■,,., ■». .I г I'life,

1П Ж Ш 2 Ш

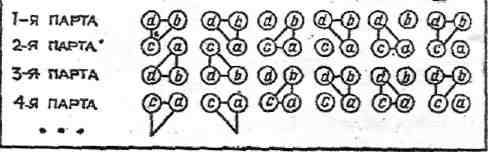
Итак, выделенные из полного звена пары и тройки не являются постоян­ными для учащихся: учитель меняет их в зависимости от цели и задач группо­вой работы.

Расскажем о работе учителя со звеньями. Как показал эксперимент, звенья из двух учеников являются эффективными при взаимопроверке и выполнен и устных упражнений.

В первом случае учащийся выполняет самостоятельно задание, данное всему классу, а затем организуется взаимопроверка в звеньях из двух учеников. Например, классу дается самостоятельная работа.

После самостоятельного выполнения заданий учащиеся проверяют друг друга, а затем под руководством учителя обсуждаются результаты самостоя­тельной работы. В данном случае последовательно осуществляется индивиду­альная, групповая и фронтальная работа.

Работа в звене-паре при выполнении устных упражнений проводится в форме, диалога между учащимися, а затем учитель организует фронтальную или коллективную работу по обсуждению полученных результатов.

Полные звенья и звенья-тройки, составленные I и II способами, эффектив­ны при организации на уроке сочетания групповой и индивидуальной работы каждого учащегося.

Звенья из трех учащихся III—VI видов эффективны при организации груп­повой работы в звене в сочетании с фронтальной или коллективной работой учащихся, не включенных в звено.

Исходя из особенностей каждой типологической группы, учитель опреде­ляет цели дифференцированной работы с учащимися и помощь, которую им можно оказать непосредственно на уроке. Например, работа учителя с группой направлена либо на ликвидацию пробелов в знаниях, умениях и навыках, либо на актуализацию знаний и умений, необходимых для изучения нового материа­ла, либо на развитие умений осуществлять самостоятельные действия по образ­цу, воспроизводить ранее изученный материал, а также на развитие интереса к предмету.

Дифференцированная работа учителя с учащимися группы А направлена либо на расширение и углубление знаний по пройденному материалу, либо на развитие умений самостоятельно и творчески работать с учебной и научно-популярной литературой, либо на развитие умений решать нестандартные творческие задачи.

Отметим, что организация групповой работы учащихся на уроке на основе звеньев из двух, трех и четырех учащихся в сочетании с другими формами дея­тельности способствует повышению эффективности обучения математики в целом.

III. Заключение (Результативный компонент).

Психологической службой школы проводилась промежуточная диагности­ка учащихся в начале 8а, 86 класса для анализа динамики эффективности обра­зовательного процесса в данных классах в сравнении с результатами входной диагностики. (Приложения)

Дифференцированное обучение на уроках математики в разноуровневом классе позволяет ученикам увидеть математику не как набор хаотически пере­мешанных фактов, никак не связанных между собой, а как стройную систему понятий, находящихся между собой в чётко определенных отношениях. Прове­денное психологическое исследование показало положительную динамику (Приложение 1-4).

Как видно из диаграмм, каждый ребенок сделал небольшой, но значитель­ный шаг в процессе развития своих способностей.

В перспективе планируется итоговая диагностика, ставящая целью опреде­ление уровня готовности учащихся к обучению, на следующей стадии обуче­ния.

Мною, вместе с психологической службой были проанализированы ре­зультаты диагностик, мы констатируем стабильность положительных результа­тов.

Выводы:

Улучшение показателей в работе дает основание считать намеченные пути правильными, а методические приемы по дифференцированному обучению за­служивающими внимания.

Я не считаю свой результат конечным. Необходимо и далее разрабатывать и совершенствовать приемы и методы дифференцированного обучения на уро­ках математики в разноуровневом классе, как личностно - ориентированный подход в обучении.

Анализируя проделанную работу педагогический опыт можно сделать ряд выводов:

1)Удалось достичь основной цели работы - выработать ряд методов, включенных в обычные программные уроки и позволяющих овладеть приема­ми дифференцированного обучения, а следовательно, облегчить усвоение мате­риала и активизировать творческие способности школьников.

2)Результатом проведенной работы является несколько методических ре­комендаций:

• В целях совершенствования преподавания математики целесооб­разна дальнейшая разработка новых методик использования не­стандартных и творческих заданий;

• Систематически использовать на уроках разноуровневые задания, способствующие формированию у каждого ребенка познавательно­го интереса и самостоятельности;

• Осуществлять целенаправленное обучение школьников решению задач, с помощью специально подобранных упражнений, учить их наблюдать, пользоваться аналогией, сравнением и делать соответ­ствующие выводы.

Таким образом, проведенная деятельность позволяет утверждать, что диф­ференцированная работа на уроках математики в разноуровневых классах дело важное и необходимое.

Литература.

1. Волович М.Б. Как успешно обучать математике. - «Математика» - прило­жение к газете «Первое сентября», 1997 г.

2. Груденов Я.И. Совершенствование методики работы учителя математики. Книга для учителя - М.: Просвещение, 1990 г.

3. Гусев В.А. Индивидуализация учебной деятельности учащихся, как основа дифференцированного обучения математике. Математика в школе. №4, 1990 г.

4. Дорофеева В.Г., Кузнецова Л.В., Суворова СВ. Дифференциация в обуче­нии математике. Математика в школе. №4, 1990 г.

5. Косунов А.Н. Уровневая дифференциация при обучении математике V -IX классах. Математика в школе. №5, 1990 г.

6. Крутецкий В.А. Психология математических способностей школьников. -М.: Просвещение, 1972 г.

7. Миндюк М.Б. Составление и использование разноуровневых заданий для дифференцированной работы с учащимися. Математика в школе. №1, 1991 г.

8. О дифференцированном обучении математике. Математика в школе. №3, 1990 г.

9. Развитие творческой деятельности учащихся, в процессе обучения (из опыта работы). Киров, 1995 г.

10. Ромашко Ш.В., Винник В.М. Технология работы в разноуровневых груп­пах. Москва, 1992 г.

11. Рыбников К.А. К вопросу о дифференциации обучения. Математика в школе. №5, 1990 г.

12. Семенов Е.Е., Малиновская В.В. Дифференцированное обучение матема­тике с позиций гуманизма. Математика в школе. №4, 1990 г.

13. Чередов И.М. Методика конструирования форм организации обучения. Омск, 1985 г.

14. Чередов И.М. О дифференцированном обучении на уроках. Омск, 1973 г.