Повышение качества образования через развитие интеллектуальных, творческих способностей учащихся на основе методической системы Л.В.Занкова.

Среди важнейших прав человека, наиважнейшим – после права на достойную жизнь – является право быть умным. Традиционная модель обучения не реализует данное право (быть не только умной, но всесторонне развитой личностью). Это право реализуется лишь в развивающей модели обучения.

Понятие «развивающего обучения» включает в себя соотношение обучения и развития. Все обучение построено на знании психологии развития. Развитие детей в данной системе понимается не в узком смысле слова, не как развитие отдельных сторон, а как общее развитие личности. Под общим развитием понимается развитие ума, воли и чувств, всех фундаментальных сторон психики. Общее развитие-это развитие наблюдательности, мышления и практических действий во всех сферах деятельности и жизни, а не только в учебной. Противоречия, сложившиеся в традиционной системе между обучением и развитием школьников, в полной мере разрешаются в развивающей модели обучения. Координально меняется распределение ролей на таком уроке: вместо привычной позиции « Учитель впереди - ребенок сзади» появляется позиция «ребенок впереди - учитель сзади или рядом». Отпустив ребенка вперед, учитель убеждается, что даже шестиклассники могут быть активными организаторами урока, что они могут давать учителю вполне разумные указания, что они могут выдвигать идеи и составлять задания, которые являются новыми и неожиданными даже для учителя, наконец, что они сами могут учить друг друга. Любой ребенок будет учиться с увлечением, если его умственная деятельность будет осуществляться в психологически комфортном режиме. Под психологически комфортным режимом обучения мы понимаем такой тип обучения, который соответствует реальному устройству детского ума и позволяет каждому ребенку самостоятельно выбирать наиболее предпочтительную для него форму интеллектуального учебного поведения, т.е. оптимальное общее развитие каждого ученика (обучение с учетом индивидуальных способностей и особенностей каждого ребенка). Главная проблема всего учебного процесса – формирование побуждений к деятельности, т.е. мотивации. И никаких позитивных результатов в образовании нельзя добиться, если у ученика нет необходимой мотивации.

На этом этапе мыслительная деятельность учащихся поднимается на более высокую ступень – интеллектуальное образование, которое состоит в развитии познавательных интересов и способностей школьников, их творческого ума, в привитии культуры умственного труда.

Отводится серьёзное внимание межличностным отношениям участников образовательного процесса. Учитывая умения учащихся в решении интеллектуальных задач, учителя-предметники создают условия для оптимального развития способностей школьника к дальнейшему самообразованию и совершенствованию.

Приняв 5-й класс, который обучался в начальной школе по дидактической системе Л.В. Занкова, появилась проблема преемственности обучения в 5 – х классах по данной системе.

Осуществляя требования преемственности, и, изучив социальный заказ родителей, я, как учитель математики, изучив теоретические положения наследия Занкова, решила реализовать технологию развивающего обучения по Л.В.Занкова.

Новые дидактические принципы, как подчеркивал Л.В. Занков, не заменяют, не развивают, не дополняют ранее сложившиеся принципы. Они возникли в логике научного исследования по проблеме изучения и развития, имеют свою взаимосвязь, свою систему, вне которой существовать не могут.

Новые дидактические принципы положены в основу отбора содержания образования и в основу его методической организации.

Преемственность обучения заключается в реализации типических свойств методической системы Л.В. Занкова: многогранности, процессуальности, коллизии, вариативности. Основной мотивацией учебной деятельности является познавательный интерес учащихся. И поэтому идея гармонизации требует сочетать в методике рациональное и эмоциональное, факты и обобщения, коллективное и индивидуальное, информационное и проблемное, объяснительный и поисковый методы обучения.

Чтобы реализовать преемственность обучения необходимо продолжить единую цель: оптимальное общее развитие каждого ученика.

В целях организации преемственности преподавания математики в классах, обучающихся по системе Л.В. Занкова, в условиях перехода в основное звено, конференцией рекомендован, как один из путей экспериментальной работы в пятых классах по математике – внедрение технологии преподавания математики, разработанной в рамках проекта «МПИ» - Математика. Психология. Интеллект»

Определены цели, тема, объект, задачи, задачи, гипотеза, критерии и показатели результативности, ожидаемые результаты, этапы деятельности.

Цель инновационного проекта – внедрить новую дидактическую систему обучения в условиях реализации преемственности обучения, обеспечивающее развитие каждого ученика.

Тема инновационного проекта «Повышение качества образования через развитие интеллектуальных, творческих способностей учащихся на основе методической системы Л.В. Занкова по математике в 5 – 11классах».

Объект исследования – учебная деятельность в основной школе.

Предмет исследования – содержание обучения математики в условиях реализации дидактической системы Л.В. Занкова в основной школе:

• Апробация учебников по математике в 5-х – 9-х классах под редакцией С.Гриншпон (авторы Э.Г. Гельфман, М.А. Холодная и другие), Центр при Томском университете.

• Средства, обеспечивающие содержание обучения.

• Процесс учения, соблюдение дидактических принципов системы общего развития школьников.

• Характер взаимоотношений участников учебно-воспитательного процесса в условиях обучения, направленного на общее развитие учащихся.

Задачи инновационной работы:

1. Применить новую методику обучения школьников (развивающую методику Л.В. Занкова) в условиях преемственности обучения математики в основной школе.

2. Апробировать экспериментальную программу по математике в среднем звене.

3. Апробировать экспериментальные учебники по математике, соответствующие экспериментальной программе.

4. Разработать инструментарий для организации мониторинга по изучению уровня общего развития учащихся основной школы.

5. Разработать систему диагностических заданий для организации мониторинга по изучению уровня обученности учащихся среднего звена.

Условия реализации инновационной работы:

1. Изучение программы начальных классов по математике.

2. Изучение нормативных документов.

3. Изучение методической литературы по теме инновационного проекта.

4. Обеспечение учебниками и учебными пособиями учащихся класса.

Методы и методики исследования

Эмпирические методы – изучение научно – методической литературы по апробации учебников; анализ школьной учительской, ученической документации, педагогические наблюдения, опросы, анкетирование, тестирование.

Теоретические методы – будут использованы при анализе, сравнении, классификации, систематизации и обобщении результатов учебной деятельности учащихся.

Гипотеза инновационной работы

Данная дидактическая система обучения способна обеспечить общее развитие учащихся в школе 2 ступени, если:

• содержание нового образования будет отражать целостную общечеловеческую культуру;

• методика ведения уроков будет соответствовать дидактическим принципам и типическим свойствам системы Л.В. Занкова;

• взаимоотношения участников учебно-воспитательного процесса будут гуманными, демократичными и строиться на сотрудничестве всех участников (учителей – детей – родителей).

Этапы инновационного проекта

I этап 5-й класс – диагностический:

II этап 6-й класс – прогностический (сентябрь – октябрь), организационно – практический (ноябрь – май);

III этап 7-й класс – практический;

IV этап 8-й класс – практический, внедрение результатов экспериментальных исследований;

V этап 9-й класс – практический, внедрение результатов экспериментальных исследований;

VI 10-й и 11-й классы – этап распространения опыта.

VII Критерии оценки ожидаемых результатов

Критерием оценки является уровневый подход (качественный показатель):

• на каком уровне трудности может работать ученик (готовность к восприятию содержания);

• уровень продвижения учащихся в общем развитии;

• уровень усвоения материала (после первичного ознакомления);

• уровень усвоения знания или умения (во всей полноте).

Ожидаемые результаты.

1. Овладеть технологией развивающего обучения (в полной мере) по Л.В. Занкову.

2. Обеспечение общего развития каждого ученика.

3. Качественный рост обученности учащихся в основной школе.

4. Сохранение здоровья детей.

Критерии и показатели обеспечения результативности экспериментально – инновационной работы

Критерии

Показатели

1. Содержание инновационной деятельности

1. Апробация экспериментальной программы и учебников по проекту «Математика. Психология, Интеллект» в 5-х – 9-х классах.

2. Обогащение содержания материала уроков алгебры и начала анализа в 10-х – 11-х классах

100% обеспеченность учащихся учебниками.

2. Средства, обеспечивающие содержание инновационной деятельности

2.1Построение урока по типическим свойствам методической системы и реализации принципов развивающего обучения на уроках математики.

- Посещение уроков руководителем творческой площадки.

- Взаимопосещение уроков учителями.

- Самоанализ уроков.

- Открытые уроки.

- Анализ уроков с позиции реализации типических свойств методической системы и принципов дидактической системы Л.В. Занкова.

3. Субъект – субъектные отношения участников образовательного процесса «Учитель – ученик – родители»

Взаимоотношения субъектов образовательного процесса.

Направленность уроков и внеклассных занятий на личность ученика, сотрудничество с учениками и родителями. Анкетирование учащихся и родителей, ознакомление с программой инновации, родительские собрания в классе о результатах экспериментальной деятельности.

4. Критерии определения общего развития учащихся

0. Изучение уровня наблюдательности учащихся.

1. Изучение уровня мыслительных операций учащихся.

2. Изучение уровня практических действий учащихся: выполнение продуктивных и творческих заданий учащимися.

3. Проведение диагностик по математике по выявлению уровня обученности учащихся.

0. Изучение уровня воспитанности учащихся.

0. Профилактика здоровья учащихся.

Результаты мониторинга изучения психологами уровня внимания и интеллекта.

Уровень продвижения учащихся в общем развитии.

Результаты диагностик по выявлению уровня выполнения творческих заданий по математике.

Результаты входных, промежуточных и итоговых диагностик по математике. Уровень обученности учащихся по математике.

Результаты диагностик по изучению уровня воспитанности учащихся.

Реализация программы «Здоровое образование учащихся».

Все выше сказанное было мною реализовано с помощью основных методов мотивации и стимулирования деятельности учащихся через:

1)эмоциональные методы мотивации:

• поощрение;

• порицание;

• учебно-познавательные игры (развивающие задачи);

• создание наглядно-образных представлений;

• создание ситуации успеха;

• стимулирующее оценивание;

• свободный выбор задания;

• удовлетворение желания быть значимой личностью.

Подробнее остановлюсь на развивающих задачах, которые можно использовать на уроках как один из эмоциональных методов мотивации, так и в целях развития познавательного интереса.

Развитие приемов мышления школьников – задание очень трудное, но необходимое. Они применяются как в математике, так и в различных областях науки и практики. Решая развивающие задачи, ученик не просто применяет практические знания, у него формируются общелогические, мыслительные умения, прежде всего связанные с применением аналогий, индуктивными умозаключениями.

Для решения развивающих задач требуется весь комплекс основных мыслительных операций. Тут и сравнение объектов, и их анализ (например, в сложной фигуре выделить элементы, которые выполняют разные функции) и синтез (построить фигуру из элементов, которые удовлетворяют данным условиям). Наибольшая нагрузка ложится на такие мыслительные операции, как абстрагирование от свойств заданных объектов, которые являются несущественными для решения задачи; обобщение, с помощью которого устанавливается основное для исследования системы отношение; конкретизация этого отношения, что позволяет определить искомый объект.

Развивающие задачи влияют на развитие наблюдательности, углубление взаимосвязи наглядно-образных и словесно-логических компонентов мышления учащихся.

Например, при изучении темы «Округление десятичных дробей» в 5 классе можно использовать на устном счете следующую задачу:

Нарисовать рисунок, которого недостаёт.

3,48

1,02 ?

по теме «Действия с отрицательными и положительными числами» учащимся была преложена следующая задача:

Найдите неизвестное число.

15-4х 3х+1=13 -1

5х-4 8-3х=2 ?

При изучении темы «Уравнения» в 6 классе на первом уроке можно использовать следующее задание. В этом задании видна связь новой темы с уже ранее изученным материалом, а так же с русским языком:

Найдите недостающее слово.

КОРКА 3х-5=2х-1 КОРА

СТОК 7х+3=3х+11 СОК

СПУСК (5х-10)(3х-12)=0 ?

Ниже приведены примеры развивающих задач, используемых мною на различных уроках:

7 класс «Графики функций». « Среднее арифметическое».

20

?

Найдите неизвестное число.

5a + 7b 41

2a – 4b ?

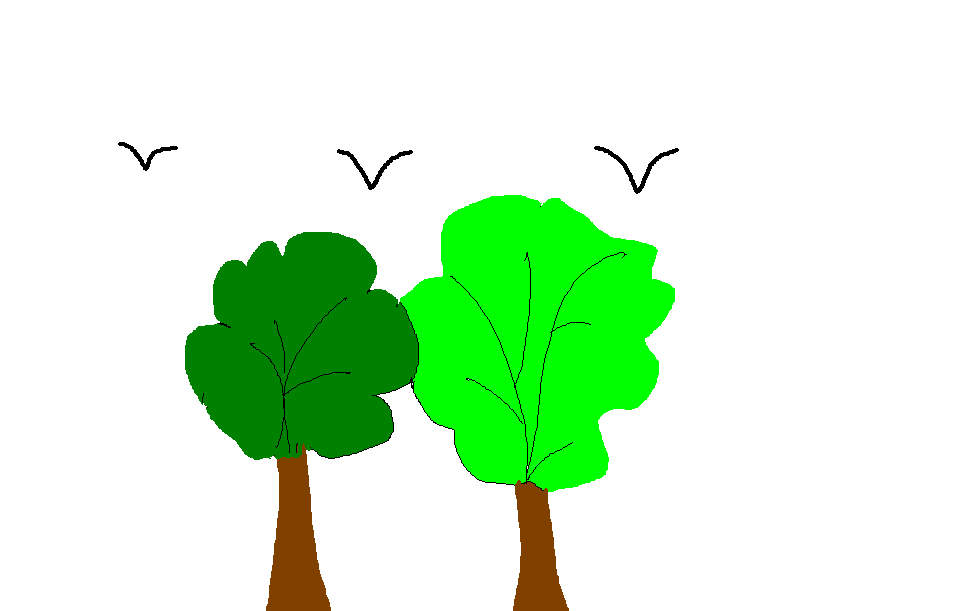
Найдите неизвестное выражение.

Опадание листьев осенью ЛИСТОПАД

(3а – в) – (а – 4в)

8 класс. «Числовые промежутки».

Найдите неизвестные числа.

-3 5 2 7 3; 4

-7 9 5 12 ?

Найдите неизвестное число.

-3 3 36

-1 1 32

-7 -4 ?

Найдите неизвестное слово.

КИТЕЛЬ 7 10 ЕЛЬ

КОЛОДКА -4 -2 ЛОДКА

ЯРМАРКА -1 2 ?

«Неравенства».

Найдите неизвестное слово.

ТРАНСПОРТ

1 ≤ х < 4 1 < х < 4

5 < х < 7 х > 5

ТРАП ?

«Осевая и центральная симметрия».

Какую из данных букв следует исключить?

Ж А П Т Н Ш Е М Ф

9 класс. « Степень с рациональным показателем».

Найдите неизвестное число.

СТОЛБ 150а^-2 + 4^3/2 14

СТОЛ

СМЕТКА 32а^-3 - 16^3/2 ?

СЕТКА

10 класс. «Решение показательных уравнений».

Найдите неизвестное слово.

КАНДАЛЫ 2^x+1 + 2^{x – 1} – 3^x-1 = 3^x-2 – 2^x-3 + 2∙3^{x - 3} КАНАЛЫ

СТОК 5∙4^x-1 – 16^x + 0,25 ∙2^2x+2 + 7 = 0 ?

11 класс. « Метод координат в пространстве».

Найдите неизвестное слово.

ПАРКЕТ а {-1; -2; 2} ПАКЕТ

.

ПЛАСТИНКА в {2; -6; 3} ?

Найдите неизвестные числа.

ШАЛАШ А (3; -4; -6) ?

ТОПОТ В (-2; 7; -5) ?

КАЗАК С (-11; -9; -1) ?

То есть практически при изучении каждой темы в своей работе учитель математики может использовать развивающие задачи.

2)Следующим методом мотивации являются познавательные методы мотивации которые включают в себя:

• опору на жизненный опыт; (Где в жизни встречаются положительные и отрицательные числа? В физике, в жизни и т.д.);

• познавательный интерес (развивающие задачи);

• создание проблемной ситуации (создание и разрешение коллизий на уроке);

• побуждение к поиску альтернативных решений (отыскание других способов решения);

• выполнение творческих заданий ( математическое лото, проекты «модуляторов», математическое домино, фигуры на координатной плоскости, рисунки, выполненные с помощью графиков функций, математические сказки, оды, теле–интервью,…).

Приведу пример использования мною такого метода познавательной мотивации как побуждение к поиску альтернативных решений.

7

1 2

3 4

класс. Тема: «Произведение многочленов».

Учащимся предложено задание:

вычислить площадь фигуры.

При решении данной задачи ребята предлагают

различные способы ее решения:

1 способ. 2 способ.

S₁ = bc; S₃ =ac; S₁₊₃= (a + b ∙c;

S₂ = bd; S₄ = ad; S₂₊₄= (a + b) ∙d;

S = bc + bd + ac + ad S = (a+ b) ∙c + (a + b) ∙ d.

3 способ. 4 способ.

S = (a + b) ∙ (c + d). S₁₊₂= (c + d )∙b;

S₃₊₄ =(c + d) ∙c;

S = (c + d)∙b+ (с + d) ∙a.

(a + b)(c +d) = ac + bc + ad + bd

После коллективного обсуждения выводится правило умножения двучлена на двучлен. Далее учитель задает учащимся вопрос:

«Какую геометрическую задачу необходимо рассмотреть для выведения правило умножения двучлена на трехчлен; умножения трехчлена на трехчлен? Что общего у всех этих задач и что у них различного?»

3) Волевые методы мотивации:

• предъявление учебных требований (на ученическом и родительском собраниях);

• информирование об обязательных результатах обучения (они должны быть вывешены на стенде по каждой теме);

• формирование ответственного отношения к учению (отражение выполнения обязательных результатов обучения и творческих заданий в открытых листах учета);

• познавательные затруднения;

• самооценка деятельности и коррекция (отражена в рефлексивных листах учащегося);

• рефлексия;

• прогнозирование.

4) СОЦИАЛЬНЫЕ МЕТОДЫ МОТИВАЦИИ:

• развитие желания быть полезным Отечеству;

• побуждение подражать сильной личности;

• создание ситуации взаимопомощи (совместная работа консультантов и слабоуспевающих учащихся);

• поиск контактов и сотрудничества;

• заинтересованность в результатах коллективной работы (групповая работа с последующим обсуждением);

• взаимопроверка (работа в парах после проведения математических диктантов);

• рецензирование (после ответа каждого отвечающего или после выступления группы).

Другим элементом урока в развивающей модели обучения является ЦЕЛЕПОЛАГАНИЕ, которое тесно связано с мотивацией.

Приведу пример целеполагания. Цель урока определяют сами учащиеся.

Тема: «Умножение целых чисел».

Учитель предоставляет возможность учащимся самим определить цель урока, исходя из итогов предыдущих уроков, на основе домашнего задания.

Учитель: Какую цель можно поставить сегодня на уроке?

Ученики: Познакомиться с умножением целых чисел.

Учитель: Познакомиться с умножением. А почему выбрали слово «познакомиться»? Почему не «осмыслить», например, или «объяснить»?

Ученики: Потому что, мы только на первой ступеньке узнавания, понимания.

Учитель записывает на доске цель урока и далее обсуждает с учащимися, каким образом можно достичь поставленной цели урока и совместно с ними составляет план изучения нового материала.

1. Смысл действия умножения.

2. Правило действия (это про то, как умножать такие числа).

3. Практическое истолкование правила.

4. Свойства умножения.

5. Частные случаи.

Далее обсуждается каждый пункт этого плана. В конце урока сами учащиеся отвечают на вопрос: Достигнута ли цель урока?

Что мы изучили, что осталось незатронутым или к какому пункту плана необходимо вернуться на следующих уроках.

То есть учащиеся ставят не только цель урока, составляют план ее достижения, но выяснят перспективы изучения темы на данном уроке и на последующих уроках (прогнозирование).

Приведу пример изучения нового материала по теме «Квадратные уравнения».

На доске записаны следующие уравнения:

1. 3(х-4)=2(х+5)-6; 6) 5х² - 2х=0;

2) (2х+3):5=0; 7) (5+х) (х-4)=7;

3) 6х² - 24=0; 8) –3х² + √5х=0;

4) (х-5)² - 16=0; 9) 19х-8(х-3)=66-3х.

5) 5х² - 2х - 3=0;

Учитель: Разбейте данные уравнения по какому-либо признаку на три группы и дайте название каждой из них.

Учащиеся предлагают свои варианты ответов. После непродолжительного обсуждения, класс приходит к нужному для данного урока ответу.

Ученики: 1 группа- 1), 2), 9) - линейные уравнения;

2. группа- 3), 6), 8) - неполные квадратные уравнения;

3. группа- 4), 5), 7)- ?

Учащиеся затруднились с названием 3 группы.

Учитель: Какую тему урока необходимо записать на доске?

Затем учитель записывает тему урока и обсуждает с учащимися цель урока и этапы ее достижения.

Для успешного обучения учащихся в своей работе я использовала разнообразные формы работы:

• коллективную - поиск нового, исходя из ранее изученного (урок-исследование);

• групповую;

• парную;

• индивидуальную.

КОЛЛЕКТИВНАЯ форма работы может быть использована на уроке изучения нового материала, когда учащимся предстоит самостоятельно исследовать новую тему, тесно связанную с ранее изученным материалом. Такой урок может быть разбит на следующие этапы:

1 этап. Постановка задачи с вытекающим составлением плана.

2 этап. Выдвижение гипотезы (идеи). Выработка инструкции (как достичь цели урока).

3 этап. Обоснование гипотезы.

ГРУППОВАЯ форма работы. Приведу пример ее использования на в 8 классе по теме «Исследование корней квадратного уравнения».

Класс разбивается на группы. Учащиеся самостоятельно работают над проблемой зависимости количества корней квадратного уравнения от его коэффициентов. Каждой группе дается задание, написанное на карточке. Например:

Какие из следующих уравнений, на ваш взгляд, имеют корни, а какие уравнения корней не имеют:

1) х² – 12х- 64 = 0; 2) 10х² – 3х + 1 = 0;

3) 100 – 20х – х² =0; 4) 2х² –16х + 18 = 0;

5) 2х² – 3 – 7х = 0?

Можете ли вы ответить на этот вопрос, не решая уравнений? Если да, то на основании чего вы сделаете свой вывод? Какую зависимость можно установить между коэффициентами количеством корней квадратного уравнения?

После самостоятельной исследовательской работы группы обмениваются мнениями и выводами о проделанной работе. Вся их работа рецензируется и делается общий вывод.

Парную форму работы лучше всего использовать при взаимопроверке, например, математического диктанта, небольшой самостоятельной работы, теоретического блиц опроса и т.д. Индивидуальная форма используется с учетом индивидуальных способностей каждого ребенка (работа у доски, работа по карточкам, беседа наедине с учителем).

Очень важным для учителя и учеников является создание учителем «комфортного климата» на уроке. Условия для создания комфортности на уроке:

1. Создание атмосферы сотрудничества и товарищества в отношениях между учителем и классом, и между учениками;

2. Использование необычных форм преподавания нового материала, причем изложение его должно быть занимательным, эмоциональным и ярким.

3. Побуждение ребят к участию в дискуссии, споре, диалоге.

4. Поощрение у учащихся готовность к сотрудничеству и взаимопомощи.

5. Делать учащимся комплименты, подбадривать их. Находить в каждом ученике что-нибудь хорошее.

6. Отражать меру усилий, затраченных учеником при выполнении оцениваемого задания.

7. Не сравнивать успехи одного ученика с успехами другого, а проводить сравнение сегодняшних результатов данного ученика с его предыдущими успехами (проводить динамику развития).

8. Стараться найти в каждом ученике и его действиях то, что заслуживает положительной оценки.

9. Сохранять доброжелательный тон, улыбаться.

10. Добиваться преобладания положительных оценочных суждений над отрицательными.

11. Использовать на уроках минуты разрядки, отдыха.

12. Само построение процесса учения создает условия для комфортности. Комфортности на уроке способствует и учет индивидуальных способностей учащихся (графический, вербальный, логический способы выполнения заданий).

13. Предоставлять свободу выбора заданий.

14. Дифференцировать задания. Выполнение разно уровневых заданий позволяет учащимся продвигаться от низкого уровня обученности к более высокому.

Немаловажным фактором повышения качества успеваемости также является и контрольно-оценочная деятельность, которая протекает на протяжении всего урока. Причем оценивает как учитель, так и ученики. Объектом данной деятельности являются и ответы одноклассников, и способ выполнения заданий, и результат коллективной деятельности класса. Учитель в начале урока характеризует работу класса на предыдущем уроке. На протяжении всего урока он побуждает ребят контролировать и оценивать ответы одноклассников, использует различные формы взаимоконтроля (рецензирование, работу в парах сменного состава, работу в группах и т.д.)

Так же для эффективного и качественного обучения на уроках можно применять такой вид контрольно-оценочной деятельности, как нахождение допущенной ошибки и приведение собственных примеров. Учитель совместно с классом подводит итог урока, побуждает ребят высказаться о том, кто и как работал, и что было усвоено, и на что необходимо обратить внимание на следующем уроке. Проводится рефлексия учащихся.

Принципиальной особенностью занковской системы является характерный подход к выявлению результативности обучения. Прежде всего, результаты обучения оценивать по показателям продвижения детей в общем развитии. Усвоение программного материала, конечно, изучается, но это не единственная цель, которая затмевает взгляд учителя на ученика, на изучение закономерностей, а не изучение знаний.

В течение года мы отслеживаем обученность учащихся (входная, промежуточная, итоговая диагностика), динамику развития мыслительных операций (1 раз в год). Параллельно с учителем, психологи проводят свои диагностики, на результаты которых я опираюсь.

Заключение.

Каковы же результаты моей деятельности по «Повышению качества образования через развитие интеллектуальных, творческих способностей учащихся на основе методической системы Л.В.Занкова»?

Во-первых, цель инновационного проекта реализована, ожидаемые результаты выполнены: я овладела методикой развивающего обучения Л.В.Занкова, обеспечено оптимальное общее развитие учащихся среднего и старшего звена.

Во-вторых, не нарушена преемственность обучения по системе Л.В.Занкова, что способствовало повышению качества образования на 32% в 2005г. по сравнению с 1999г.

В-третьих, накоплен большой теоретический и практический материал, создан весь учебно-методический комплекс, разработаны методические рекомендации по проведению уроков самоконтроля.

В-четвертых, учащиеся 11 класса показали не только высокие результаты по итоговой диагностики, но и повышение уровня мыслительных операций на 64% в 2005г. по сравнению с 1999г.

В-пятых, были успешно апробированы учебники математики серии «МПИ» с 5-го по 9-й классы.

Итак, за период с 1998 – 2005 гг. мною был накоплен опыт в преподавании математики по дидактической системе Л.В.Занкова.

Реализуя методику развивающего обучения на уроках математики с 5-го по 11-й классы, можно сделать следующий вывод:

1. учащиеся активнее включаются в учебную деятельность;

2. умеют использовать ранее полученные знания в новой ситуации;

3. при организации совместной работы в группах, парах умеют сотрудничать, проявляют чувства коллективизма, коммуникативности;

4. на высоком уровне владеют общеинтеллектуальными навыками (умеют анализировать, группировать, классифицировать, обобщать, выделять закономерности, находить ошибки);

5. умеют терпимо относиться к мнению другого, доказывать свою точку зрения, оппонировать, прогнозировать свою деятельность.

Самое главное (на данном этапе жизни) – наши дети умеют учиться, саморазвиваться. Мы живем в эпоху перемен, в непрерывно развивающемся мире. А раз развивается мир, надо учить человека саморазвиваться.

Список литературы

1. Гаштут А.Г. Развивающие задачи. Киев, 1988 г.

2. Нечаева Н.К. Л.В. Занков – педагог, психолог. Москва, 1996 г.

3. Холодная М.А. Психология интеллекта: парадоксы исследования. Москва – Томск, 1997 г.

4. Бухвалов В.А. Технологии работы учителя – мастера. Рига, 1999г.

5. Зверева М. В. О дидактических принципах. Москва, 2002г.

6. Тихомирова Л.Ф. Развитие интеллектуальных способностей школьника. Ярославль, 1997 г.

17