Решения олимпиадных задач

для учащихся 5-7 классов

Автор: Зубова Анна Николаевна

учитель математики

Математические ребусы:

Задача 1. Какую цифру заменяет черный треугольник?

В примере на сложение:

► + ► + ○○ = Δ Δ Δ

различные фигурки заменяют различные цифры.

Какую цифру заменяет черный треугольник?

Решение: Максимальное значение суммы трех наших слагаемых равно 9 + 9 + 99 = 117. Значит, Δ Δ Δ = 111. Минимальное значение числа ○○ равно 111 - 9 - 9 = 93, а само число равно 99. На долю одного черного треугольника приходится (111 - 99) : 2 = 6.

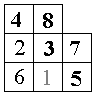
Задача 2. Расставьте цифры 1, 2, 3, ..., 8 в клетки неполного квадрата так,

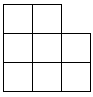чтобы получить одинаковые суммы по горизонталям, вертикалям и большой диагонали.

Решение:

Задача 3. Найдите цифры, вместо которых стоят звездочки:

А) * 8 *

4 * 2

-------

7 * 0

* * *

* * * *

--------------

* * * * 2 *

Решение: Усмотреть, что последняя цифра в первом числе – это 0 или 5, а первая цифра – 3, а затем перебрать несколько вариантов.

Ответ: 385·412=158620.

Б) найдите цифры, которые стоят вместо букв.

Арифметика.

Задача1: Если кенгуру научится прыгать в 1,5 раза дальше, чем умеет, ему понадобится ровно 6 прыжков, чтобы добраться до тенистого дерева. За сколько прыжков кенгуру может это сделать сейчас?

Решение: Чем короче прыжок, тем больше их надо сделать, чтобы добраться до тенистого дерева. Следовательно, кенгуру понадобится сделать 1,5 Х 6 = 9 прыжков.

Задача2: Автобусный билет будем считать счастливым, если между его цифрами можно в нужных местах расставить знаки четырёх арифметических действий и скобки так, чтобы значение полученного выражения равнялось 100. Является ли счастливым билет N123456?

Решение:

1 + (2 + 3 + 4) . (5 + 6) = 100. Есть и другие решения (попробуйте найти ещё хотя бы одно).

Их разность также делится на искомое число: 96-72=24.

Следовательно, искомое число - 24, так как на него делится и 96, и 72.

Задача 3: Сколько надо поставить знаков «плюс» между цифрами числа 987 654 321, чтобы в сумме получилось 99?

Решение: 9 + 8 + 7 + 65 + 4 + 3 + 2 + 1 = 99 или 9 + 8 + 7 + 6 + 5 + 43 + 21 = 99.

Задача 4: Востановите последовательность чисел и найдите ее сумму: 1+2+3+....+75+76+77

Решение: ((1+77)+(2+76)+...+(38+40))+39=78*38+39=3003

Задача 5: Используя только знаки математических действий и скобки, изобразите тысячу шестью пятёрками.

Решение: (55 − 5) × (5 × 5 − 5) = 1000

5 × (5 + 5) × (5 × 5 − 5) = 1000

(5 + 5) × (5 + 5) × (5 + 5) = 1000

Задача 6: . Мальвина велела Буратино умножить число на 4 и к результату прибавить 15, а Буратино умножил число на 15 и потом прибавил 4, однако, ответ получился верный. Какое это было число?

Решение Обозначим искомое число через х и запишем уравнение: 4х + 15 = 15х + 4. Решая это уравнение, получим: 11 = 11х, или х = 1.

Задачи на взвешивания.

Задача 1: У Буратино есть 27 золотых монет. Но известно, что Кот Базилио заменил одну монету на фальшивую, а она по весу тяжелее настоящих. Как за три взвешивания на чашечных весах без гирь Буратино определить фальшивую монету?

Решение: Разделим монеты на 3 кучки по 9 монет. Положим на чаши весов первую и вторую кучки; по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка (если весы покажут равенство, то она - в третьей кучке). Теперь, аналогично, разделим выбранную кучку на три части по три монеты, положим на весы две из этих частей и определим, в какой из частей находится фальшивая монета. Наконец, остается из трех монет определить более тяжелую: кладем на чаши весов по 1 монете - фальшивкой является более тяжелая; если же на весах равенство, то фальшивой является третья монета из части. Задача решена.

Задача 2:В пакете содержится 9 кг крупы. Требуется при помощи чашечных весов с гирями в 50 и 200 г распределить всю крупу по двум пакетам: в один — 2 кг, в другой — 7 кг. При этом разрешается произвести только 3 взвешивания.

Решение: Надо произвести следующие три взвешивания:

1)Развесить крупу на 2 равные части (это можно сделать без гирь).

2)Одну из получившихся частей ещё раз развесить пополам — по 2,25 кг.

3)От одной из этих частей отвесить (при помощи гирь) 250 г. Останется 2 кг.

Задача 3: Как разложить на 3 равные кучки 1002 гирьки, имеющие вес 1, 2, 3, ..., 1002 г?

Решение: Будем раскладывать гирьки в порядке возрастания их весов в три мысленно пронумерованные кучки, поочередно начиная то с № 1, то с № 3.

Кучка №1 1 6 7 12 ... 997 1002

Кучка №2 2 5 8 11 ... 998 1001

Кучка №3 3 4 9 10 ... 999 1000

Задачи на переливания.

Задача 1: Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал?

Решение:

Как в результате можно получить 4 л? Нужно из 5-литрового сосуда отлить 1 л. А как это сделать? Нужно в 3-литровом сосуде иметь ровно 2 л. Как их получить? – Из 5-литрового сосуда отлить 3 л.

Решение лучше и удобнее оформить в виде таблицы:

Шаг

Сосуд – 3л

Сосуд – 5л

1

0

5

2

3

2

3

0

2

4

2

0

5

2

5

6

3

4

Наполняем из бочки 5-литровый сосуд медом (1 шаг). Из 5-литрового сосуда отливаем 3 л в 3-литровый сосуд (2 шаг). Теперь в 5-литровом сосуде осталось 2 литра меда. Выливаем из 3-литрового сосуда мед назад в бочку (3 шаг). Теперь из 5-литрового сосуда выливаем те 2 литра меда в 3-литровый сосуд (4 шаг). Наполняем из бочки 5-литровый сосуд медом (5 шаг). И из 5-литрового сосуда дополняем медом 3-литровый сосуд. Получаем 4 литра меда в 5-литровом сосуде (6 шаг). Задача решена.

Задача 2: Имеются сосуды – 17 л и 5 л. Как отмерить 13 л?

Решение:

1-й шаг: налить в сосуд 17 л 3 раза по 5 л, т.е. 15 л.

2-й шаг: наполнить 5-литровый сосуд и 2 литра вылить в сосуд 17 л, там будет 17 л, а в

5-литровом останется 3 л.

3-й шаг: вылить воду из сосуда 17 л, а туда слить 3 л и налить 2 раза по 5 л.

Логические задачи:

«Правдивые задачи»

Задача 1: В одном городе кто-то угнал машину у градоначальника. Полиция задержала троих человек: Джона, Джека и Джо. Полиции было известно, что один из них - лжец, один - всегда говорит правду, а про третьего точно неизвестно, говорит ли он правду или ложь. Полиция также знала, что один из них угнал машину, и что этот человек всегда говорит правду. Три человека сказали следующее:

Джон: Я не виновен. Джек: Он говорит истинную правду.

Джо: Я угнал машину.

Кто угнал машину и кто лжец?

Решение: Джон сказал: "Я не виновен". По условию задачи два человека являются невиновными: лжец и шутник. Джон не может быть лжецом, так как лжец, в данном случае, сказал бы, что он виновет. Джон не может быть и правдолюбцем, так правдолюбец виновен, и он не сможет сказать неправду. Остается, что Джон шутник, при этом он говорит правду, так как он, действительно невиновен. Джек подтверждает невиновность шутника Джона, т.е. Джек говорит правду, поэтому он не лжец, а правдолюбец, Джек и угнал машину. Джо - лжец и как положено лжецу, он всех обманывает, говоря, что он угнал машину.

Метод рассуждений

Задача 1: У рассеянной хозяйки есть три ящика для рассады с надписью "Огурцы", "Цветы" и "Ромашки". Она посадила семена ромашек, огурцов и колокольчиков в эти ящики так, что все надписи оказались неверными. Что вырастет в ящике с надписью "Ромашки"?

Решение: В силу своей рассеянности, хозяйка не могла посадить в ящик с названием "Цветы" ни ромашки, ни колокольчики. Следовательно, она посадила в этом ящике огурцы. Теперь осталось ей посадить ромашки и колокольчики. Для них осталось два ящика с надписями: "Ромашки" и "Огурцы". Но рассеянная хозяйка не посадила ромашки в ящик с названием "Ромашки", как они того они заслуживали, а посадила их в ящик под названием "Огурцы". А колокольчики она посадила в ящик с надписью "Ромашки".

Задача 2: В семье четверо детей. Им 5, 8, 13 и 15 лет. Детей зовут Галя, Коля, Валя и Таня. Сколько лет каждому ребенку, если известно, что одна девочка ходит в детский сад, Галя старше Коли и сумма лет Гали и Вали делится на три?

Решение. Сначала найдем возраст мальчика. Поскольку в детский сад ходит девочка, то это не Коля. Тогда Коле больше 5 лет. Так как Галя старше Коли, то Коле не может быть 15 лет. Если сумма лет Гали и Вали делится на три, то, учитывая возраст детей в семье, это возможно в следующих случаях:

1) одной девочке 5, а другой 13 лет;

2) одной девочке 8, а другой 13 лет.

В обоих случаях одной из девочек 13 лет, следовательно, Коле не может быть 13 лет. Зная, что Коле не 5, не 15 и не 13 лет, приходим к выводу, что мальчику 8 лет.

Теперь установим возраст каждой девочки. Поскольку сумма лет Гали и Вали делится на три, а Коле 8 лет, этим двум девочкам 5 и 13 лет. А так как по условию Галя старше Коли, то Гале 13 лет. Тогда Вале должно быть 5 лет, а Тане 15 лет.

Метод таблиц

Задача1: Живут-поживают пять зайчат: Попрыгунчик, Ушастик, Тишка, Зайка, Беляк, и у каждого есть мячик. Цвета мячиков такие: синий, зеленый, красный, желтый и оранжевый. У Ушастика мячик желтого цвета, а у Зайки не зеленый, не синий и не красный. У Попрыгунчика был бы синий мячик, если бы у беляка был зеленый мячик, но у беляка мячик другого цвета. Беляк не любит игрушки синего цвета. У кого какой мячик?

Решение: У Ушастика желтый мячик. (Ставим плюс в Ячейку «Желтый, Ушастик», а во все остальные ячейки столбца «Ушастик» и строку «Желтый» заполняем минусами). У Зайки не зеленый, не синий и не красный мячик, значит – оранжевый. (Ставим плюс в ячейку «Оранжевый, Зайка», заполняем свободные ячейки столбца и строки минусами). Так как у Беляка мячик не зеленый и не синий(ставим минусы), не желтый и не оранжевый, значит у него мячик красного цвета. Так как у Прыгунчика не синий мячик, значит у него зеленый. Получаем, что у Тишки мячик синий.

Цвет мячика

Кличка зайчика

Прыгунчик

Ушастик

Тишка

Зайка

Беляк

Зеленый

+

-

-

-

-

Синий

-

-

+

-

-

Красный

-

-

-

-

+

Желтый

-

+

-

-

-

Оранжевый

-

-

-

+

-

Задача 2: В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. «Замечательно, что один из нас блондин, другой — брюнет, а третий — рыжий, и при этом ни у одного из нас цвет волос не соответствует фамилии», — заметил черноволосый. «Ты прав», — сказал Белов. Определите цвет волос художника.

Решение: Ясно, что в решении будет рассматриваться только взаимное соответствие фамилий и цветов волос друзей, профессии в рассуждении не участвуют. Поэтому в задаче нужно ответить на вопрос, какого цвета волосы у Рыжова. Воспользуемся таблицей 3x3:

Задача 3: Четыре соседа Миша, Леня, Женя и Костя ходят в спортивные секции: бокса, тенниса, баскетбола и гимнастики (каждый из мальчишек занимается только одним видом спорта). Они же владеют различными иностранными языками (английским, французским, немецким и испанским),

но каждый только одним. Известно, что:

1) мальчик, который играет в баскетбол, говорит по-испански;

2) Леня не занимается гимнастикой, не ходит в секцию бокса и не владеет английским языком;

3) Миша не занимается гимнастикой, не ходит в секцию бокса и не владеет английским языком;

4) Женя знает французский язык, но не занимается гимнастикой.

Кто в какую секцию ходит и какой иностранный язык знает?

Решение: Для решения задачи воспользуемся таблицами:

Таким образом, задача имеет два варианта решения:

1) Костя занимается гимнастикой и говорит на английском языке, Женя занимается боксом и владеет французским, Миша играет в теннис и говорит на немецком, Леня играет в баскетбол и говорит по-испански.

2) Костя занимается гимнастикой и говорит на английском языке, Женя занимается боксом и владеет французским, Миша играет в баскетбол и говорит по-испански, Леня играет в теннис и говорит по-немецки

Метод граф. Граф – очень популярный объект в математике – есть набор точек, соединенных отрезками – ребрами. Граф отлично моделирует передвижения объекта между географическими объектами, компьютерные сети, знакомства, отношения. Графы помогают лучше понять структуру исследуемого объекта.

Задача1: В школьной столовой на первое можно заказать щи, гороховый суп и борщ, на второе – котлету и рыбу, а на третье - чай и морс. Сколько вариантов обеда можно получить из указанных блюд?

Обед

Борщ Гороховый суп Щи

Рыба Котлета Рыба Котлета Рыба Котлета

М Ч М Ч М Ч М Ч М Ч М Ч

Ответ: 12 вариантов

Задача 2: сколько трехзначных чисел можно составить из цифр 1,3,5,7, используя в записи числа каждую из них не более одного раза?

Решение: составим дерево возможных вариантов.

Эту задачу можно решить по-другому и намного быстрее, не строя дерева возможных вариантов. Рассуждать будем так. Первую цифру трехзначного числа можно выбрать четырьмя способами. Так как после выбора первой цифры останутся три, то вторую цифру можно выбрать из оставшихся цифр уже тремя способами. Наконец, третью цифру можно выбрать (из оставшихся двух) двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 4∙3∙2, т.е. 24.

Задача 3: Из города А в город В ведут две дороги, из города В в город С – три дороги, из города С до пристани – две дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?

Решение: Пусть из города А в В туристы могут выбрать двумя способами. Далее в каждом случае они могут проехать из В в С тремя способами. Значит, имеется 2∙3 вариантов маршрута из А в С. Так как из города С на пристань можно попасть двумя способами, то всего существует 2∙3∙2=12 способов выбора туристами маршрута из города А к пристани.

Метод Кругов Эйлера.

Задача 5: Часть жителей города умеет говорить только по-русски, часть – только по-узбекски и часть умеет говорить на обоих языках. По-узбекски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?

Решение: Составим схему –

У ? Р

85% 75%

В кружке под буквой «У» обозначим жителей, говорящих по-узбекски, под буквой «Р» - по-русски. В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «У» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%).

Задача 2: Из 40 учащихся 5 класса 32 ходят на кружок «Умелые руки», 21 посещают спортивную секцию, 15 учащихся ходят и на кружок, и на секцию. Сколько учащихся не ходят ни на этот кружок ни на эту секцию?

Решение:

1) 32–15=17 – столько человек ходят только на кружок.

2) 17+21=38 – столько человек ходят или на секцию, или на кружок, или туда и туда.

3) 40–38=2 – никуда не ходят

Ответ: 2.

Задача 3: В классе всего 36 человек. Учащиеся посещают математический, физический и химический кружки, причем, математический кружок посещают 18 человек, физический - 14 человек, химический - 10 человек. Кроме того, известно, что все три кружка посещают 2 человека, математический и физический -8, математический и химический - 5, физический и химический - 3. Сколько учеников класса не посещают никаких кружков?

Решение:

1) 18-(2+6+3)= 7 человек посещают только мат. кружок

2) 14-(2+6+1)= 5 посещают только физ. кружок

3)10-(2+3+1)= 4 посещают только хим. кружок

4)36-(2+6+3+1)-(7+5+4)= 8 человек не посещают никаких кружков.

Задачи на движение.

Задача 1: От потолка комнаты вертикально вниз по стене поползли две мухи. Спустившись до пола, они поползли обратно. Первая муха ползла в оба конца с одной и той же скоростью, а вторая хотя и поднималась вдвое медленнее первой, но зато спускалась вдвое быстрее. Какая из мух раньше приползет обратно? У какой из мух выше средняя скорость движения?

Решение: Первая муха, конечно, приползёт раньше. Пока вторая муха доберётся до верха, первая успеет сползать туда и обратно (так как её скорость в это время в два раза больше).

Задача 2:Таракан Валентин объявил, что умеет бегать со скоростью 50 м/мин. Ему не поверили, и правильно: на самом деле Валентин всё перепутал и думал, что в метре 60 сантиметров, а в минуте 100 секунд. С какой скоростью (в "нормальных" м/мин) бегает таракан Валентин?

Решение: Валентин пробегает 50*60=3000 см за 100 с, то есть его скорость 30 см/с, что составляет 18 м/мин.

Задача 3: Группа туристов должна была прибыть на вокзал в 5 ч. К этому времени с турбазы за ними должен был прийти автобус. Однако, прибыв на вокзал в 3 ч 10 минут, туристы пошли пешком на турбазу. Встретив на дороге автобус, они сели в него и прибыли на турбазу на 20 минут раньше предусмотренного времени. С какой скоростью шли туристы до встречи с автобусом, если скорость автобуса 60 км/ч?

Решение: 6 км/ч. Туристы сэкономили 20 минут, за это время автобус дважды проехал бы путь, который они прошли, а шли они 100 минут.

Задача 4: Два охотника отправились одновременно навстречу друг другу из двух деревень, расстояние между которыми 18 км. Первый шел со скоростью 5 км/ч, а второй – 4 км/ч. Первый охотник взял с собой собаку, которая бежала со скоростью 8 км/ч. Собака сразу же побежала навстречу второму охотнику, встретила его, тявкнула, повернула и с той же скоростью побежала навстречу хозяину, и так далее. Так она бегала до тех пор, пока охотники не встретились. Сколько километров она пробежала?

Решение: До встречи охотников пройдёт два часа, за это время собака пробежала 16 км.

Задача 5: Буратино сел в поезд. Проехав половину всего пути, он лёг спать и спал до тех пор, пока не осталось проехать половину того пути, который он проспал. Какую часть всего пути Буратино проехал бодрствующим?

Решение: Обозначим через s отрезок пути, который Буратино проехал от того момента, как проснулся, до конца. Тогда путь, который Буратино проспал, составит 2s. Всего же от момента, как Буратино заснул, он проехал путь 2s + s = 3s. Но известно, что это — половина всего пути. Значит, длина всего пути 6s. Поскольку же бодрствующим Буратино проехал путь 4s, то по отношению ко всему пути эта часть составит 2/3 пути.

Задачи на работу.

Задача1: Котенок Малыш может облизать себя с головы до кончика хвоста за полчаса, а кот Тоша может облизать Малыша за 5 минут. Себя Тоша способен помыть за 20 минут. Сколько времени придется трудиться Малышу, чтобы помыть Тошу?

Решение: Малыш облизывает сам себя в 6 раз (30мин/5мин=6) медленнее, чем его облизывает кот Тоша. Тоша облизывает себя за 20 минут. Следовательно, Малыш оближет кота Тошу за 20мин · 6=120мин=2часа.

Задача 2: Лене нужно 6 часов, чтобы вымыть полы во всем доме,

Гриша и Миша пачкают каждый час 1/18 всех полов.

Сколько времени понадобится Лене, чтобы привести полы в порядок, если к началу работы все полы были грязные?

Решение: Управляясь с уборкой за 6 часов, Лена за каждый час работы вымывает 1/6 часть всех полов. В то же время два ее братца успевают за тот же час выпачкать 1/18 часть всех полов. В случае, если вся троица одновременно приступит к работе, ежечасно очищаемая часть пола составит 1/6 - 1/18 = 1/9. Следовательно, уборка продлится 1 : 1/9 = 9 часов.

Задача3: 7 волков съедают 7 баранов за 7 дней. За сколько дней 9 волков съедят 9 баранов?

Решение: Семь волков съедают семь баранов за семь дней, значит один волк съедает одного барана за семь дней. А девять волков съедят девять баранов за те же семь дней.

Задача4: Четыре чёрные коровы и три рыжие дают за 5 дней столько молока, сколько три чёрные коровы и пять рыжих дают за 4 дня. У каких коров больше удои, у чёрных или у рыжих?

Решение: Наше условие, по существу, означает, что 20 чёрных коров и 15 рыжих дают за день столько же молока, сколько 12 чёрных и 20 рыжих. А это значит, что 8 чёрных коров дают молока столько же, сколько 5 рыжих. Отсюда заключаем, что у рыжих коров удои больше.

Задача 5: Ванна заполняется холодной водой за 6 минут 40 секунд, горячей — за 8 минут. Кроме того, если из полной ванны вынуть пробку, вода вытечет за 13 минут 20 секунд. Сколько времени понадобится, чтобы наполнить ванну полностью, при условии, что открыты оба крана, но ванна не заткнута пробкой?

Решение: Сначала заменим время в секундах временем в минутах: 6 минут 40 секунд заменим на 6 + 2/3, или 20/3, а 13 минут 20 секунд заменим на 13 + 1/3, или 40/3. Тогда за одну минуту холодной водой заполнится 3/20 ванны, горячей — 1/8 ванны, а вытечет 3/40 ванны. Следовательно, за одну минуту наполнится (3/20) + (1/8) - (3/40), т.е. (1/5) ванны. Значит, вся ванна наполнится за 5 минут.

Задачи на раскраску .

Задача1. В каждой клетке доски 5×5 клеток сидел жук. Затем каждый жук переполз на соседнюю (по стороне) клетку. Докажите, что осталась хотя бы одна пустая клетка.

Решение: раскрасим доску в 2 цвета. Черных клеток-13, а белых 12. При переползании с черных клеток жуки переползали на белые и наоборот. Так как белых клеток 12, а черных на одну больше и все жуки с белых переползают на черные, то одна черная клетка останется.

Ответ : останется 1 черная клетка.

Задача2. На части шахматной доски 3×3клетки в одной из клеток стоит конь. Можно ли им обойти все девять клеток этой части доски?

Решение: если бы это было возможно, то конь должен был бы попасть в среднюю клетку, но тогда ему вообще некуда ходить на данной части доски, и в эту клетку, значит, он попасть не может.

Задача3: Можно ли замостить костями домино размером 1^х2 шахматную доску размером 8^х8, из которой вырезаны два противоположных угловых поля?

Решение: вырезаны поля одного цвета, пусть для определенности черного. Поэтому остается 32 белых и 30 черных клеток. Так как кость домино всегда накрывает одну белую и одну черную клетку, то костями домино нельзя замостить шахматную доску 8^х8 клеток, из которой вырезаны два противоположных угловых поля.

Задача4: Докажите, что доску размером 10^х10 клеток нельзя разрезать на фигурки в форме буквы Т, состоящие из четырех клеток.

Решение: Предположим, что доска 10^х10 клеток разбита на такие фигурки. Каждая фигурка содержит либо 1, либо 3 черные клетки, т.е. всегда нечетное число. Самих фигурок должно быть 100/4=25 штук. Поэтому они содержат нечетное число черных клеток, а всего черных клеток 100/2=50 штук. Получено противоречие.

Задачи на разрезание.

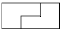
Задача 1: Как разрезать прямоугольник 4 × 9 на две части так, чтобы из них можно было сложить квадрат? Решение:

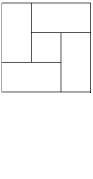
Задача 2: Сделайте из квадрата четыре равных прямоугольника и один квадрат. Решение:

Задача3: Попробуйте разрезать изображенную на рисунке фигуру на 3 равные по форме части:

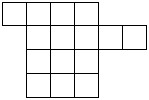Решение:

Задача 4: Разрежьте теперь эту фигуру на 4 равные по форме части:

Решение:

Задачи на четность

Задача1. Кузнечик прыгал вдоль прямой и вернулся в исходную точку (длина прыжка 1м). Докажите, что он сделал чётное число прыжков.

Решение. Поскольку кузнечик вернулся в исходную точку. Количество прыжков вправо равно количеству прыжков влево, поэтому общее количество прыжков чётно.

Задача2. На доске написаны в строку 2011 целых числа. Доказать, что если одно из них можно стереть, то сумма оставшихся будет четной. Верно ли это утверждение для 2012 чисел?

Решение: если количество нечетных чисел нечетное, то можно стереть любое из них и сумма чисел будет четным числом. Если же количество нечетных чисел четное, то при стирании любого из них сумма оставшихся чисел нечетная.

Задача3.

- У нас в классе 35 человек. И можешь себе представить, каждый дружит ровно с 11 одноклассниками…

- Не может этого быть, - сразу ответил своему приятелю Витя Иванов, победитель математической олимпиады. Почему он так решил?

Решение: Витя Иванов мог рассуждать так:

- Докажу методом от противного. Принесу в класс много веревок. Попрошу каждых двух друзей взять в руки по концу веревки, соединяющих их. А всего в классе 35×11=385 концов. Но у веревки два конца, и общее число концов тоже должно быть четным. Получается противоречие.

Ответ: такого распределения друзей быть не может.

Задача4. Шахматный конь начинает свой маршрут из левого нижнего угла доски, а кончает его в правом верхнем углу. Может ли при этом конь побывать на всех полях доски в точности по одному разу?

Решение: при каждом ходе конь меняет цвет поля. Так как начальное и конечное поля одного цвета, то конь сделает четное число ходов. Но это противоречит тому, что надо коню сделать 63 хода, чтобы побывать на каждом поле.

Ответ: не может.

Задачи на делимость

Задача 1: Остаток от деления 100 на некоторое число равен 4. При делении 90 на это же число в остатке получается 18. На какое число делили?

Решение: Из условия следует, что 100-4=96 делится на искомое число. Также 90-18=72 делится на искомое число. Их разность также делится на искомое число: 96-72=24. Найдем НОД (96;72)=24

Задача 2: Какую цифру нужно приписать к числу 97 справа и слева, чтобы полученное число делилось на 27?

Решение: Удвоенная неизвестная цифра дополняет сумму известных цифр числа до величины, кратной 9-ти. Сумма известных чисел - четная (16). Удвоенная неизвестная цифра (a) - также четная величина. Следовательно, сумма цифр искомого числа - четная и равна 18-ти. (2a меньше или равна 18 и сумма цифр искомого числа не больше 34-х). Итак, a = 1, искомое число - 1971.

Задача3: Пекарь замесил тесто, из которого можно выпечь 20 одинаковых калачей или 25 одинаковых булочек. Сколько теста в замесе, если известно, что на один калач идет теста на 10 граммов больше, чем на одну булочку ?

Решение: Масса приготовленного теста выражается числом, которое делится на 20 или на 25. Наименьшее общее кратное чисел 20 и 25 - 100. Если предположить, что в замесе 100 граммов теста, то на один калач должно уходить на 1 грамм теста больше, чем по условию. Следовательно, теста в замесе было в 10 раз больше, т.е. 1 килограмм.

Задача 4: Найти наименьшее натуральное число, которое при делении на 7 дает в остатке 6, а при делении на 9 остаток равен 8.

Решение: В обоих случаях - как при делении искомого числа на 7, так и при делении его на 9 остаток на единицу меньше делителя. Увеличив делимое на 1, получим число, которое делится без остатка и на 7, и на 9. Наименьшее такое число - 63. Искомое число на 1 меньше и равно 62.

Задача 5: Коля и Вася живут в одном доме, на каждой лестничной клетке которого 4 квартиры. Коля живет на пятом этаже, в квартире 83, а Вася - на 3-ем этаже в квартире 169. Сколько этажей в доме ?

Решение: Если вести сквозной отсчет этажей, начиная с первого подъезда, то Коля живет на 21- м этаже [83 : 4] = 20 (3). В своем подъезде Коля живет на 5-м этаже, поэтому в подъездах, предшествующих Колиному, 16 этажей. 16 делится лишь на числа, кратные 2-м, поэтому в доме может быть либо 16 этажей, либо 8 этажей (вариант четырехэтажного дома исключаем, поскольку Коля живет на 5 этаже). Вася живет на 43 этаже, считая от первого этажа первого подъезда [169 : 4] = 42 (1). Значит в подъездах, предшествующих Васиному, 40 этажей. 40 делится на 8, но не делится на 16, следовательно, в доме 8 этажей.

Задачи на проценты и отношения

Задача1: Влажность купленного арбуза составила 99%. В результате длительного хранения влажность снизилась до 98%. Как изменилась влажность арбуза?

Решение: Свежий арбуз на 99% процентов состотит из жидкости и на 1% - из сухой массы. В результате усушки количество жидкости уменьшилось и составило 98% от новой, также уменьшившейся массы арбуза. Количество же сухого вещества, оставаясь неизменным, составило 2% от новой массы арбуза. Процентное содержание в арбузе сухого вещества (при неизменной его массе) увеличилось вдвое. Следовательно масса арбуза в результате усушки уменьшилась вдвое.

Задача2: В тридесятом царстве живут драконы. У каждого дракона одна, две или три головы, а) Может ли у 40 % драконов быть 60 % голов?

Решение: Покажем, что у 40% драконов может быть 60% голов. Пусть в этом царстве живет 100 драконов: 40 драконов с одной головой, 20 – с двумя головами и 40 – с тремя. Тогда число голов у всех драконов равно 40 • 1 + 20 • 2 + 40 • 3 = 200. При этом все 40 трехглавых драконов, что составляет 40% от общего числа драконов, имеют 40 • 3 = 120 голов, что составляет 120/200 • 100% = 60% от общего числа голов.

Задача 3: У Пети в бутылке было "Фанты" на 10% больше, чем у Васи. Петя отпил из своей бутылки 11% ее содержимого, а Вася из своей – 2% содержимого. У кого после этого осталось больше "Фанты"?

Решение: Пусть у Васи в бутылке было a мл "Фанты", тогда у Пети было 1,1a мл. После того, как каждый мальчик отпил из своей бутылки, у Васи осталось 0,98a мл, а у Пети – 0,89·1,1a = 0,979a мл. Ответ: У Васи.

Задача 4: Условие В классе учится меньше 50 школьников. За контрольную работу седьмая часть учеников получила пятёрки, третья — четвёрки, половина — тройки. Остальные работы были оценены как неудовлетворительные. Сколько было таких работ?

Решение: Поскольку число школьников, получивших ту или иную оценку, всегда целое, то для решения задачи нам надо найти целое число, меньшее 50, одновременно делящееся на 7, 3, 2. Единственным возможным ответом является число 42. Это значит, что всего в классе 42 ученика; 6 из них получили пятёрки; 14 — четвёрки; 21 — тройки. Следовательно, двойку получил 1 ученик.

Задача 5: У Вани было некоторое количество печенья; он сколько-то съел, а потом к нему в гости пришла Таня, и оставшееся печенье они разделили поровну. Оказалось, что Ваня съел в пять раз больше печений, чем Таня. Какую долю от всего печенья Ваня съел к моменту Таниного прихода?

Решение: Пусть Таня съела x печений. Тогда Ваня съел 5x печений, из которых 5x-x=4x печений он съел до прихода Тани. Так как всего печений было 5x+x=6x , до Таниного прихода Ваня съел = всего печенья.

Задачи, решаемые с конца.

Задача1: Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки. Дедка, Бабка, Внучка, Жучка и Кошка вместе с Мышкой могут вытащить Репку, а без Мышки — не могут. Сколько надо позвать Мышек, чтобы они смогли сами вытащить Репку?

Решение: Кошка заменяет 6 Мышек. Жучка заменяет 5•6 Мышек. Внучка заменяет 4•5•6 Мышек. Бабка заменяет 3•4•5•6 Мышек. Дедка заменяет 2•3•4•5•6 Мышек. Итого потребуется:

(2•3•4•5•6) + (3•4•5•6) + (4•5•6) + (5•6) + 6 + 1 = 1237 Мышек.

Задача 2: В озере растут лотосы. За сутки каждый лотос делится пополам, и вместо одного лотоса появляются два. Ещё через сутки каждый из получившихся лотосов делится пополам и так далее. Через 30 суток озеро полностью покрылось лотосами. Через какое время озеро было заполнено наполовину?

Решение: Если вы прочтёте условие задачи внимательно, то поймёте, что озеро было заполнено наполовину через 29 суток. За сутки до того, как озеро заполнится, оно будет заполнено ровно наполовину.

Задача3: Три мальчика делили 120 фантиков. Сначала Петя дал Ване и Толе столько фантиков, сколько у них было. Затем Ваня дал Толе и Пете столько, сколько у них стало. И, наконец, Толя дал Пете и Ване столько, сколько у них к этому времени имелось. В результате всем досталось поровну. Сколько было фантиков у каждого вначале?

Решение: Мы знаем, что в конце у всех оказалось по 40 фантиков. А перед этим у Пети и Вани было вдвое меньше. Значит, у Пети и Вани было вдвое меньше – по 20, а у Толи – 80. А перед этим у Пети и Толи было вдвое меньше, т.е. у Пети было 10, у Толи 40, у Вани – 70. И, наконец, возьмём половину фантиков у Вани и Толи и вернём Пете.

Ответ: у Пети было 65 фантиков, у Вани – 20, а у Толи – 35.

Задача 4: Над имеющимся числом разрешается производить два действия: умножить его на два или прибавить к нему 2. За какое минимальное число действий можно из единицы получить триста?

Решение: Задача решается с конца:

1) 300:2=150, 2)150-2=148,

3) 148:2=74, 4) 74-2=72,

5) 72:2=36, 6) 36:2=18,

7) 18-2=16, 8) 16:2=8,

9) 8:2=4, 10) 4:2=2,

11) 2:2=1

Задача 5: Однажды Чёрт предложил бездельнику заработать. «Как только ты перейдёшь через этот мост, - сказал он, - твои деньги удвоятся. Можешь переходить по нему сколько хочешь раз, но после каждого перехода отдавай мне за это 24 копейки». Бездельник согласился и …после третьего перехода остался без гроша. Сколько денег у него было сначала?

Решение: Задача решается с конца. Так как после третьего перехода у бездельника денег не осталось, то после перехода моста в третий раз у него было ещё 24 копейки, а до перехода третьего моста – 12 копеек. Тогда после перехода второго моста у бездельника было12 = 24 = 36 копеек, а до перехода второго моста – 36:2 = 18 копеек. Рассуждая аналогично, получим, что после перехода первого моста у бездельника стало 18 +24 = 42 копейки, а перед переходом первого моста – 42 : 2 = 21 копейка. Таким образом, у бездельника сначала была 21 копейка.

Геометрические задачи

Задача 1: Фигурка из двух одинаковых деталей

Какую из фигурок A - E нельзя составить из двух одинаковых деталей, изображенных справа?

Детали нельзя переворачивать тыльной стороной вверх.

ответ D

Задача 2: Где домик Пятачка?

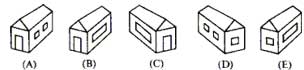
Домик Кролика нарисован 4 раза, а домик Пятачка только один раз.

Где домик Пятачка? ответ В

Задача 3: Размышляем над кубиком

От кубика, склеенного из бумаги, отрезали уголок.

Этот кубик разрезали по некоторым ребрам, развернули и получили одну из фигурок A - E. Какую?

ответ Е

Задача 4: Человек прикинул в уме, что он может выложить пол комнаты, имеющей квадратную форму, квадратной плиткой, и что ему не понадобится ни одну из них разрезать. Сначала, он положил плитки по краям комнаты, и на это у него ушло 56 плиток. Найдите, сколько всего ему надо иметь плиток, чтобы покрыть весь пол?

Решение: Угловая плитка учитывается один раз, поэтому между боковыми плитками находится (56-4) :4=13. В следующем ряду между боковыми плитками находится 11 и тогда количество плиток будет (11×4)+4=48, в следующем ряду (9×4)+4=40, и т.д. Количество плиток : 56+48+40+32+24+16+8+1=195

Задача 5: С помощью циркуля и линейки разделить угол в 19° на 19 равных частей.

Решение: Ясно, что задача сводится к построению угла в 1°, далее все просто. Заметим, что 19 х 19 = 361, то есть сумма девятнадцати углов в 19° есть окружность плюс 1°. Сложение углов при помощи циркуля и линейки является стандартной, хорошо решаемой задачей. Получив угол в 1°, далее отложим этот угол девятнадцать раз и получим угол в 19°. Задача решена.

Задача 6: Нарисовать треугольник, который можно разделить на 5 равных треугольников.

Решение: Очевидно, что треугольник можно разделить на 4 равные части. Далее к этому треугольнику требуется «приставить» его четвертую часть; при этом снова должен получиться треугольник. Это возможно только в том случае, когда треугольник является прямоугольным, ведь только тогда сумма двух прямых углов даст развернутый угол (отрезок, который является стороной треугольника, при этом будет суммой сторон большого треугольника и его «четвертушки»).

Покажем на рисунке решение задачи. Необходимо нарисовать прямоугольный треугольник, у которого один катет в два раза длиннее другого.

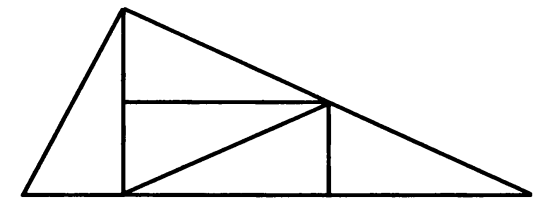
Памятка участнику олимпиады.

1. Прочитайте все задачи и наметьте, в каком порядке вы будете их решать. Помните последние задачи обычно более сложные.

2. Если для вас задача решалась слишком легко, то, скорее всего вы не поняли условие или где-то ошиблись.

3. Если задача не решается – попробуйте упростить ее условие (взять меньшие числа, рассмотреть частные случаи и т.д) или порешать ее «с конца», «от противного», поставить вместо чисел переменные и т.д.

4. Не зацикливайтесь на на одной задаче: иногда отрывайтесь от нее и оценивайте положение. Если есть хоть небольшие успехи, то можно продолжать, а если мысль ходит по кругу, то задачу лучше оставить, хотя бы на время.

5. Почувствовав усталость – отдохните (посмотрите в окно, закройте глаза, отвлекитесь).

6. Решив задачу, сразу оформите ее решение. Это поможет проверить рассуждения и освободить мысли для других задач.

7. Перед сдачей работы, проверьте еще раз написанное – поймут ли ваши решения задач члены жури?