Квантовые приборы

Содержание

Введение

Оптоэлектронные приборы широко применяются в передовых отраслях промышленности, электроаппаратуре и используются, в основном, для генерации, передачи, хранения и отображения информации. Важнейшими из них являются лазеры, их техническую основу определяют конструктивнотехнологические концепции современной электроники: миниатюризация элементов, предпочтительное развитие твердотельных плоскостных конструкций, интеграция элементов и функций и др.

Полупроводниковые лазеры отличаются от газовых и твердотельных тем, что излучающие переходы происходят в полупроводниковом материале не между дискретными энергетическими состояниями электрона, а между парой широких энергетических зон. Поэтому переход электрона из зоны проводимости в валентную зону с последующей рекомбинацией приводит к излучению, лежащему в относительно широком спектральном интервале и составляющему несколько десятков нанометров, что намного шире полосы излучения газовых или твердотельных лазеров. Кроме того, полупроводниковые лазеры технологичнее, особенно с точки зрения их получения в комплексе со смежной микроэлектроникой, учитывая ориентацию на специальные сверхчистые материалы и применение методов групповой обработки изделий, таких как эпитаксия, фотолитография, нанесение тонких пленок, диффузия, ионная имплантация, плазмохимия и др.

Цель работы проанализировать основные аспекты квантовой электроники и дать характеристику квантовых приборов.

Задачи

1. Рассмотреть основы квантовой электроники;

2. Дать характеристику квантового парамагнитного усилителя;

3. Охарактеризовать твердотельные и жидкостные лазеры.

Глава 1. Основы квантовой электроники

1.1. Основные понятия квантовой электроники

Квантовыми приборами (КП) называются устройства, служащие для генерации или преобразования электромагнитных колебаний оптического и СВЧ - диапазона, действие которых основано на преобразовании внутренней энергии возбужденных квантовых систем в энергию электромагнитного поля.

Квантовые приборы

Квантовая система

Ансамбль квантовых систем

Энергетические уровни

Молекулярные

Электронные

Атомные (ионные)

Рис. 1.1 - Концептуальная диаграмма КП

Квантовой системой называется такая элементарная частица или совокупность элементарных частиц (атом, молекула, газ, кристалл твердого тела, жидкость), состояния которой дискретно (квантованы), т.е. составляют строго определенный для данной системы набор состояний с дискретными значениями внутренней энергии в каждом из этих состояний [4]. Разрешенные значения энергии элементарных частиц и всей квантовой системы называются энергетическими уровнями. Однако некоторые состояния квантовой системы имеющие одинаковую энергию могут качественно отличаться друг от друга. Такие состояния называются вырожденными. Число различных состояний с одинаковой энергией определяет степень вырождения состояния. Рассмотрим главные особенности основных типов квантовых систем, используемых в квантовых приборах.

а) Атомные (ионные) квантовые системы

Согласно основам квантовой механики дискретные значения в атоме (ионе) имеют: энергия электрона W, абсолютные значения орбитального момента количества движения электрона 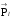_, значение его проекции 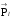и значение проекции собственного момента количества движения 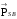на произвольные направления внешнего магнитного поля с индукцией В. Спектры возможных значений этих величин даются выражениями [4]:

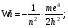n =1, 2, 3, ......

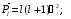l = 1,2,3, .....

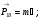m = 0, ± 1, ± 2, ± 3, .... ± l

Набор разрешенных энергетических уровней (энергетический спектр) графически представляется в виде энергетических диаграмм.

W

0

W₁

W₂

W₃

W_n

W_m

Энергетическая диаграмма атома представлена на рис. 1.2.

Рис. 1.2 - Энергетическая диаграмма атома

Электроны стремятся занять уровни с наименьшей энергией, что соответствует состоянию устойчивого равновесия атома [2]. Однако если электрону сообщить дополнительную порцию энергии извне, он может перейти на более высокий энергетический уровень. Для этого необходимо, чтобы дополнительная энергия ∆W была равна ширине энергетического зазора между уровнями перехода: ∆W = W_n - W_m. Такое состояние квантовой системы (в данном случае атома) называется возбужденным. В возбужденном состоянии квантовая система находится недолго (обычно 10^-6 - 10^-10 с) и самопроизвольно возвращается в исходное состояние, т.е. электрон возвращается на нижний уровень. Внешнее электромагнитное поле может изменить энергию только самых внешних электронов атома (иона), т.к. среднее расстояние между внешними электронным уровнями составляет ∆W = 1 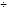10 эВ (1эВ = 1,6 · 10^-19 Дж), что соответствует видимой области оптического диапазона. Действительно [4]

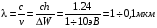
б) Молекулярные квантовые системы

Состояние многоатомной молекулы слагается из электронных состояний составляющих молекулу атомов, из состояний колебательного движения атомов относительно центра масс этих атомов и состояний вращательного движения молекулы. Все три перечисленные компоненты квантованы. Переходы из одного колебательного состояния в другое происходят с изменением энергии ∆W = 0,01 0,1эВ, что соответствует длинам волн 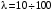мкм (дальняя инфракрасная область оптического диапазона). Наконец, при переходе между состояниями вращательного движения атомов излучается или поглощается энергия ∆W=0,001 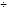0,01эВ, что соответствует длине волн с 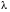=100 мкм 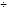1мм. Таким образом, используя энергетические переходы между различными состояниями можно получить излучение (поглощение) электромагнитных колебаний с различной частотой.

в) Электронные квантовые системы

Твердые тела, в том числе полупроводники, представляют собой системы, состоящие из двух взаимодействующих подсистем - подсистемы атомных остовов (кристаллическая решетка) и подсистемы валентных электронов [6]. Это вторая подсистема обладает зонной структурой энергетического спектра и может изменять свое состояние при изменении температуры или под действием электрического поля, освещения и т.п. Как мы увидим далее, такие электронные квантовые системы также могут служить в качестве «рабочего вещества» квантовых приборов.

1.2. Виды взаимодействия квантового ансамбля с полем

При всех взаимодействиях с веществом поле поглощается и испускается отдельными порциями, которые получили название квантов света или фотонов. Каждый фотон обладает энергией W= hn и импульсом [4]

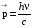
Взаимодействие квантового ансамбля с электромагнитным полем может проявляться в одном из следующих видов:

а) Спонтанное (самопроизвольное) излучение.

Рассмотрим два энергетических уровня W_m и W_n квантовых систем данного ансамбля (рис. 1.3).

hv

W_n

W_m

W

Рис. 1.3 - Энергетические уровни квантовых систем ансамбля

Эти уровни обязательно должны удовлетворять правилу отбора, согласно которому, например, в простейших атомных системах значение орбитального квантового числа в рассматриваемых состояниях отличались на ±1. Допустим, что квантовая систем переходит из состояния n в состояние m. При этом ее энергия уменьшится на величину W_n-W_m. Эта энергия превратится либо в тепло, либо в энергию фотона. Если при переходе не нарушится закон сохранения момента количества движения, то излучится фотон, частота которого определится равенством [5]

hn = W_n - W_m (1)

Число спонтанно генерируемых фотонов за единицу времени в единице объема среды равно

n_ФС = В_C N_n , (2)

где В_C - коэффициент Эйнштейна, или вероятность спонтанного перехода квантовой системы из состояния n в состояние m; N_n -населенность уровня W_n в расчете на единицу объема.

б) Поглощение излучения. Если фотон частоты n, удовлетворяющей соотношению (1), сталкивается с квантовой системой, находящейся в состоянии W_m , то система переходит в состояние W_n , а фотон исчезает. Число поглощаемых в единице объема в единицу времени фотонов будет равно

n_ФГ = В_ПN_mN_Ф , (3)

где В_П - коэффициент Эйнштейна для поглощения, равный произведению вероятности встречи фотона и квантовой системы за единицу времени в расчете на один фотон и одну квантовую систему и вероятности поглощения фотона при этом. N_m - населенность уровня W_m в единице объема, N_Ф - число фотонов в том же объеме [5].

в) Вынужденное (индуцированное) излучение. Если фотон частоты n при своем распространении в среде сталкивается с квантовой системой в состоянии W_n, то в результате вызванного этим столкновением возмущения квантовой системы она переходит в состояние W_m с излучением нового фотона. Число актов такого вынужденного излучения в единицу времени в единице объема будет равно

n_ФН = В_ИN_mN_Ф , (4)

где В_И - коэффициент Эйнштейна для вынужденного излучения. Теория и опыт показывают, что для невырожденных уровней W_n и W_m коэффициенты В_И и В_П одинаковы.

Фотоны, возникающие в результате вынужденного излучения, являются точной копией фотонов вызвавших излучение - имеют ту же частоту, то же направление движения, одинаковую начальную фазу и одинаковую поляризацию.

Как следует из (1) населенность уровней в квантовом ансамбле при термодинамическом равновесии убывает с ростом энергии уровней, что можно записать в виде следующей формулы [4]

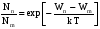, (5)

Но тогда из (2.5)следует, что всякое вещество в термодинамическом равновесии не может усиливать электромагнитные колебания, т.к. в каждом элементе объема среды будет поглощаться больше фотонов, чем их генерируется в этом объеме. Усиление будет иметь место, если N_n >N_m, т. е. населенность верхнего активного уровня больше населенности нижнего уровня.

Состояние квантового ансамбля с N_n >N_m называется инверсией (обращением) населенностей уровней. Используя формулу (2.5), можно показать, что инверсия населенностей соответствует отрицательной температуре. Действительно, прологарифмировав обе части равенства, находим, что поскольку ln (N_n /N_m) > 0 и (W_n-W_m) > 0, то Т < 0. Однако абсолютная отрицательная температура физического смысла не имеет. Это понятие применимо лишь для описания населенностей двух энергетических уровней. Физическая среда, в которой достигается инверсия населенностей уровней, называется активной средой.

Таким образом, квантовое усиление электромагнитных колебаний может быть получено при прохождении их через активную среду с отрицательной температурой [2].

В определенных условиях активная среда способна генерировать электромагнитное излучение, частота которого равна частоте перехода между уровнями, удовлетворяющих условию N_n >N_m. Для этого активное вещество необходимо поместить в полый резонатор, например, в виде «зеркальной» сферы с достаточно высоким коэффициентом отражения. В такой сфере почти каждый фотон будет отражен поверхностью сферы и вновь возвратится в объем активного вещества.

В веществе происходят акты спонтанного перехода квантовых систем из верхнего состояния в нижнее с излучением фотона. Этот фотон при своем движении либо поглотится веществом, либо «произведет» на свет другой, подобный себе, фотон. Если N_n >N_m, то вероятность поглощения меньше вероятности вынужденного излучения.

Значит, через некоторое время в объеме вещества будет уже 2 фотона, затем 4 и т.д. Плотность когерентного излучения внутри сферы будет нарастать до тех пор, пока число фотонов, уходящих за пределы сферы, не станет равным числу фотонов, рождающихся внутри сферы в единицу времени за счет вынужденных переходов квантовых систем из верхнего энергетического состояния в нижнее. Установится устойчивый режим генерации [3].

То, что на языке фотонов звучит как зеркало, на языке волновых представлений означает просто проводящую поверхность, а «зеркальная сфера» - это «полый резонатор», добротность которого Q эквивалентна коэффициенту отражения a.

Значит, для получения квантового генератора необходимо активное вещество поместить в полый резонатор с достаточно большой добротностью.

Глава 2. Квантовый парамагнитный усилитель

2.1. Квантовые парамагнитные усилители

Квантовые парамагнитные усилители (КПУ) - сверхвысокочастотные приборы, в которых усиление электромагнитных колебаний происходит за счет вынужденного излучения, обусловленного парамагнитным резонансом [4].

Парамагнетизм наблюдается у атомов переходной группы с неполностью заполненной электронной оболочкой. Вследствие этого результирующий магнитный момент атома (иона) отличен от нуля и имеет спиновую природу.

Типы усилителей

КПУ

Парамагнетизм

Эффект Зеемана

Создание инверсии населенностей

Фактор Ланде

Бегущей волны

Резонансный

Квантовые числа

Рис. 2.1 - Концептуальная диаграмма КПУ

В КПУ используются диэлектрические ионные кристаллы рубина (Аl₂O₃), рутила (ТiO₂), вольфраматa (MgWO₄) с примесью ионов парамагнитных атомов Сr³⁺ или Fе³⁺ и другие вещества. Ансамбль этих парамагнитных ионов и составляет, собственно, активную среду усилителя.

Наиболее широкое применение получили КПУ на рубине. Рубин - это кристалл корунда (Аl₂О₃), в котором небольшая часть (менее 0,1%) диамагнитных ионов алюминия замещена парамагнитными ионами хрома.

В сложных атомах орбитальные моменты количества движения электронов незаполненной оболочки совместно образуют общий орбитальный момент количества движения атома с квантовым числом L [8]. Квантовое число L в зависимости от взаимной ориентации орбитальных моментов электронов принимает значения отличающиеся друг от друга на 1 и заключенных между максимальным и минимальным значениями модуля алгебраической суммы орбитальных квантовых чисел отдельных электронов. Аналогичным образом через модуль алгебраической суммы спиновых чисел электронов определяется квантовое число S.

Наряду с квантовыми числами L и S вводится квантовое число J, определяющее квадрат величины полного момента количества движения атома по формуле h²J(J+1). Квантовое число J при заданных L и S может принимать значения L + S, L+S-1, ... |L-S|, т.е. в случае S£ L, 2S+1 значений. Если L < S, то J может принимать 2L+1 различных значений. Так как каждому значению J соответствует определенная энергия взаимодействия, то спин - орбитальное взаимодействие приводит к тому, что каждый одиночный вырожденный энергетический уровень расщепляется на 2S+1 или 2L+1 подуровня. Расчеты показывают, что энергия атома в каждом его стационарном состоянии (задаваемом числами L,S,J) при наличии внешнего магнитного поля напряженностью Н изменится на величину

∆W=gP₀HM_J , (6)

где g - так называемый гиромагнитный фактор или фактор Ланде, определяемый числами L, S, J;

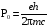- магнетон Бора,

где е, m - соответственно заряд и масса электрона, с - скорость света. При L=0 магнитный момент атома имеет чисто спиновое происхождение и g=2.

Так как магнитное квантовое число М_J имеет 2J + 1 различных значений, то согласно (4) каждый стационарный энергетический уровень атома расщепляется в магнитном ионе на 2J + 1 уровней. Расстояние между соседними уровнями (∆M_J =1) равно

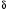W=gP₀H (7)

Расщепление энергетических уровней атома в магнитном поле носит название эффекта Зеемана. Этот эффект широко используется в квантовых приборах СВЧ диапазона для получения системы с наперед заданным расстоянием между энергетическими уровнями [9].

2.2. Конструкция КПУ и их параметры

КПУ как и всякие усилители СВЧ диапазона, подразделяются на усилители резонансного типа и усилители типа бегущей волны [4]. В соответствии с принципом действия конструкция КПУ должна включать резонатор или замедляющую систему, электромагнит из сверхпроводников для создания поля необходимой величины, генератор накачки с перестраиваемой частотой, систему вентилей для обеспечения нужного направления потока электромагнитной энергии.

На рис. 2.2 показан проходной резонаторный КПУ.

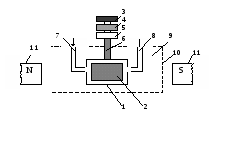
Рис. 2.2 - Устройство проходного резонатора КПУ:

1. Резонатор; 2. Парамагнетик; 3. Генератор накачки; 4. Ферритовый вентиль; 5. Аттенюатор; 6. Вход мощности накачки; 7. Линия передачи входного сигнала; 8. Линия передачи выходного сигнала; 9. 10.Сосуды Дьюара; 11. Магнит.

Генератор накачки через развязывающий ферритовый вентиль и аттенюатор, регулирующий уровень мощности накачки, подключается к резонатору.

Для уменьшения коэффициента шума, увеличения коэффициента усиления и КПД КПУ резонатор и частично СВЧ линии охлаждаются до температуры жидкого гелия (4,2К). Для этого они помещаются в криостат, образованный двумя сосудами Дьюара, из которых внутренний заполнен жидким гелием, а внешний - жидким азотом [6].

Под действием постоянного магнитного поля в кристалле рубина (парамагнетик) происходит Зеемановское расщепление энергетических уровней ионов хрома. Изменяя ориентацию кристалла или величину магнитного поля выбирается диаграмма расщепленных уровней, рабочий переход и переход накачки. Под действием сигнала накачки в кристалле возникает инверсия населенностей уровней. Входной сигнал, проходя через активный кристалл, вызывает вынужденные переходы, благодаря чему и происходит его усиление.

Квантовые парамагнитные усилители обладают очень низким уровнем шумов и высокой чувствительностью. Поэтому КПУ используют в качестве высокочувствительных СВЧ усилителей. В то же время они представляют собой довольно громоздкие устройства. Поэтому КПУ эксплуатируются в стационарных установках в радиоастрономии, сверхдальней космической связи, радиолокации и т.п. Резонаторные КПУ на частотах 1-10 ГГц при использовании рубина имеют коэффициент усиления 15-30 дБ и полосу менее 1%.

Глава 3. Твердотельные и жидкостные лазеры

3.1. Лазеры на рубине

Лазер на рубине исторически был первым твёрдотельным лазером (760г.). Основу рубина составляет корунд - окись алюминия (А1₂Оз), в кристаллической решётке которого часть ионов алюминия (0.015...0.05%) замещена ионами трёхвалентного хрома Сr³⁺.

Органические красители

Лазеры

Твердотельные

На рубине

Жидкостные

Режим свободной генерации

Режим с модулированной добротностью

На основе растворов красителей

Неорганические красители

Рис. 3.1 - Концептуальная диаграмма

Диаграмма энергетических уровней хрома приведена на рисунке 3.2. Уровень 1 соответствует основному (невозбуждённому) состоянию ионов хрома [7]. При облучении кристалла рубина светом мощной ксеноновой лампы накачки ионы хрома поглощают излучение и переходят из основного состояния 1 на два широких уровня 3. В результате теплового взаимодействия с кристаллической решёткой через 10^-7...10^-8с после возбуждения происходит спонтанный безызлучательный переход ионов хрома в метастабильное состояние, соответствующее подуровням 2 (время жизни на этих двух уровнях велико и составляет примерно 3 ּ10^-3с). Это позволяет накапливать на уровнях 2 большое количество активных частиц, т.е. уровни 2 будут инверсно населены относительно уровня 1.

Теперь, при наличии положительной обратной связи в резонаторе лазера достаточно появления первичных спонтанных переходов ионов хрома с одного из подуровней 2, чтобы возникло излучение либо с λ=0,6963 мкм, либо с λ = 0,6929 мкм. При этом чаще всего реализуется режим с излучением на волне λ = 0,6943 мкм, поскольку он отличается более низким порогом генерации.

W

3

3

2

2

1

l=0,6943 мкм

l=0,6929 мкм

накачка

генерация

Рис. 3.2 - Диаграмма энергетических уровней хрома [4]

Режим свободной генерации может быть при непрерывной и импульсной накачках. В этом режиме формирование импульсов излучения начинается с момента достижения порога генерации и длится в течение всего периода действия накачки. Длительность импульсов излучения составляет десятки микросекунд. Этот режим применяется для получения больших энергий в импульсе, которая колеблется от долей джоуля до 400 Дж. Частота повторения импульсов для разных типов генераторов 0,005..5Гц, средняя мощность генераторов равна 0,1..30 Вт.

Во всех лазерах для охлаждения элементов используется замкнутая система водяного охлаждения. Лазеры такого типа применяются в основном для технологических целей - сверления отверстий, резки, плавки, сварки тугоплавких металлов.

Этот режим используется для получения коротких (10...50 нс) импульсов излучения с крутым фронтом [6]. Этот режим обеспечивается введением между непрозрачным зеркалом резонатора и активным элементом (рубином) светового затвора, который в интервале времени от начала импульса световой накачки до момента достижения максимальной инверсии населённости уровней в активной среде вносит в резонатор большие потери.

В зависимости от способа управления потерями (коэффициентом пропускания) различают несколько типов световых затворов: оптико-механический, фототропные (фототропность - свойство веществ менять прозрачность под воздействием света), электрооптические и акустооптические.

Импульсная мощность, получаемая при длительности импульсов порядка 15...20 нс доставляет 10⁶...10⁷ Вт. При этом в конструкциях лазеров на рубине наибольшее распространение получили оптико-механические и акустооптические затворы.

Твёрдотельные лазеры применяются в технологии; в военной технике в качестве передатчиков лазерных дальномеров; в системах самонаведения ракет, бомб и снарядов; в лазерной локации; в системах подводного наблюдения; в метеорологии.

3.2. Лазеры на жидкостях

Лазеры на основе растворов красителей (ЛК) занимают особое место прежде всего благодаря присущей этим активным средам большой ширине линий излучения, что позволяет создавать на их основе генераторы оптического когерентного излучения, перестраиваемые в большом оптическом диапазоне.

Для накачки ЛК используется как излучение лазеров других типов, так и излучение некогерентных источников - ламп накачки.

По принципу действия ЛК - четырёхуровневые системы, так как в структуре их энергетических уровней нижний лазерный уровень не совпадает с основным невозбуждённым уровнем, а находится несколько выше него, что предопределяет низкий порог возбуждения ЛК.

Важным преимуществом жидкой активной среды является отсутствие технологических трудностей, связанных с изготовлением активной среды, в которой к тому же отсутствуют потери излучения из-за неоднородностей структуры [9].

Наиболее эффективно ЛК работают в режиме излучения коротких импульсов длительностью порядка 10... 20 нс.

Число красителей, генерирующих в широком спектральном диапазоне от ультрафиолетовой до ближней инфракрасной области спектра, исчисляется многими десятками. В лазерах на основе органических красителей используются растворы родамина, пиронина, трипафлавина, карбостирила, кумарина. Растворителями служат вода, спирты, глицерин.

Кроме растворов органических красителей используются растворы редкоземельных хелатов и растворы неорганических соединений редкоземельных элементов. Редкоземельные хелаты представляют собой сложные органические комплексы, в которых ионы редкоземельного элемента находятся в окружении атомов кислорода, принадлежащих к органическим молекулам. Из них наиболее перспективен бензолацетанат европия. Длина волны излучения λ = 0,65 мкм.

В лазерах на неорганических соединениях используются растворы солей неодима Nd в оксихлориде селена SeOCl₂.

Конструкция жидкостного лазера подобна конструкции твёрдотельного с тем отличием, что вместо стержня в резонатор помещается кювета с раствором. Инверсия, как и в твёрдотельном лазере, осуществляется с помощью оптической накачки от импульсных ламп. Средняя мощность излучения достигает 380 Вт, а импульсная 50 МВт (в режиме модуляции добротности).

Заключение

Широкий спектр применения квантовых оптических приборов позволяет решать многие задачи, лежащие как в областях проектирования электроаппаратуры, так и в областях технологии её производства.

Внедрение гетероструктур позволило не только улучшить основные характеристики полупроводниковых лазеров, но и создавать принципиально новые узкопрофильные устройства для применения в научных исследованиях и высокотехнологичных производствах. Так, в частности, найдено решение задачи создания приборов с прямозонной энергетической диаграммой, что не удавалось реализовать на гомогенных структурах.

Прозрачность широкозонного эмиттера для рекомбинационного излучения базы гетерогенной структуры существенно облегчает задачу конструирования излучательных приборов.

Лазеры на основе растворов красителей (ЛК) занимают особое место прежде всего благодаря присущей этим активным средам большой ширине линий излучения, что позволяет создавать на их основе генераторы оптического когерентного излучения, перестраиваемые в большом оптическом диапазоне.

Список использованной литературы

1. Абдуллаев А.М. - Электронные и квантовые приборы. Часть 1. - Т: ТЭИС,1999.

2. Андреев И.С., Арипов Х.К., Кузьмина Г.Н. - Электронные и квантовые приборы. Часть 1. - Т; ТЭИС,1998.

3. Андрушко Л.М., Фёдоров Н.Д. Электронные и квантовые приборы СВЧ. М: Радио связь, 1981.

4. Арипов Х.К., Кузьмина Г.Н., Абдуллаев А.М., Афанасьева А.М. Квантовые приборы. Конспект лекций - Ташкент: ТУИТ 2004. – 40 с.

5. Елисеев П. Г. Введение в физику инжекционных лазеров. М.: Микроэлектроника, 1993. – 10 c.

6. Крылов К. И., Прокопенко В. Т., Тарлыков В. А. Основы лазерной техники. М.: Машиностроение, 1990. – 12 c.

7. Рябов С. Г. Приборы квантовой электроники. М.: Радио и связь, 1985. – 8 с.

8. Рябов С.Г., Торопкин Г.Н., Усольцев Н.Ф. - Приборы квантовой электроники. - М: Радио и связь, 1985.

9. Фёдоров Н.Д. - Электронные приборы СВЧ и квантовые приборы. Изд.2-е. - М: Атомиздат, 1979.

22