работа по Теории автоматического управления
 Московский Государственный Технический Университет имени Н. Э. Баумана
Московский Государственный Технический Университет имени Н. Э. Баумана
Курсовая работа по
Теории автоматического управления
Выполнил
студент группы СМ7-71
Олеванов С. А.
Руководитель
Чемоданов Б.К.
Москва, 2005 г.
Содержание
Часть 1.
1. Техническое задание……………………………………………………………….....………3
2. Вывод уравнения исполнительной части………………………………………......……….4
3. Построение желаемой ЛАЧХ………………………………………………...……..………..6
3.1. Нахождение координат рабочей точки…………………….……………..….……6
3.2. Построение желаемой ЛАЧХ………………………………………….………..….7
3.3. Расчет параллельного корректирующего устройства………………….….…..….7
3.4. Техническая реализация параллельного КУ…………………………….….…..…9
3.5. Проверка устойчивости внутреннего контура…………………………..……...…9
3.6. Проверка устойчивости всей системы……………………………….….………..10
4. Аналоговая САР с возмущающим воздействием………………………………………….10
5. Введение связи по возмущающему воздействию………………………………………….13
Часть 2.
1. Техническое задание…………………………………………………………….…..………15
2. Построение желаемой ЛАЧХ..……………………………………..………………….……15
3. Расчет параллельного корректирующего устройства...…………..………………….……16
4. Техническая реализация параллельного КУ ………………….…………………...………18
5. Проверка устойчивости внутреннего контура…………….…..…..………………….……18
6. Проверка устойчивости всей системы……….…………….…………………..…..…….…19
7. Переходный процесс САУ...………………….…………….…..…..…………………….…19
8. Расчет коэффициентов усиления устройств, входящих в САУ………………….…….....20
Часть 3.
1.Введение нелинейности…………………………………………………….…..……………21
ЧАСТЬ 1.
Техническое задание.
Спроектировать следящую САУ, согласно Схеме 1, в соответствии со следующими параметрами:
Момен тинерции, приведенный к валу двигателя:
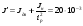 [кг·м2]
[кг·м2]
Передаточное число редуктора : iр = 650,
Номинальный момент двигателя: Мдв.н = 7.2 [Н·м],
Возмущающий момент на валу двигателя Мс = 0.3·Мдв.н,
Номинальный ток двигателя: Iд.н = 4 [A],
Сопротивление якорной цепи: Rя = 0.4 [Ом],
Электрическая постоянная времени: Тэ = 0.1 [c],
Номинальная скорость вращения двигателя: nдв.н = 2500 [об/мин],
Номинальное напряжение двигателя: Uдв.н = 220 [В],
Скорость изменения управляющего воздействия:
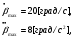
Максимальная ошибка:
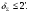
2. Нахождение уравнения силовой части.
Выведем уравнение исполнительной части следящей системы. В системе в качестве исполнительного двигателя используется двигатель постоянного тока независимого возбуждения, схема которого представлена на Рис. 1.
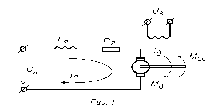
Запишем уравнения, согласно схеме замещения:
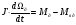 (2.1),
(2.1),
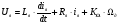 (2.2),
(2.2),
где 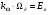 (2.3),
(2.3),
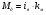 (2.4).
(2.4).
Uя – напряжение якоря,
Iя – ток якоря,
Lя – индуктивность якоря,
Rя – активное сопротивление якоря,
J’ – суммарный момент инерции, приведенный к валу двигателя,
Мд – момент, развиваемый двигателем,
Мвд – момент возмущения, приведенный к валу двигателя,
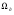 - скорость вращения ротора двигателя,
- скорость вращения ротора двигателя,
Ея – противо-ЭДС,
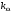 - коэффициент противо-ЭДС (конструктивная постоянная двигателя),
- коэффициент противо-ЭДС (конструктивная постоянная двигателя),
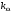 kм – конструктивная постоянная двигателя.
kм – конструктивная постоянная двигателя.
Рассмотрим уравнения (1) – (4).
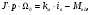
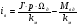 (2.5).
(2.5).
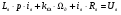 ,
,
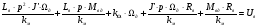 ,
,


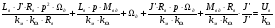 .
.
Обозначим:
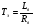 - постоянная времени нарастания тока якоря (из-за наличия Lя) (2.6),
- постоянная времени нарастания тока якоря (из-за наличия Lя) (2.6),
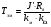 - постоянная времени нарастания скорости ИД. (2.7).
- постоянная времени нарастания скорости ИД. (2.7).
Подставив данные обозначения получим:
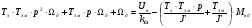 ,
,
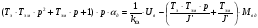 (2.8),
(2.8),
Примем:
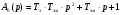 (2.9).
(2.9).
Найдём значение Тэм:
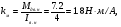 (2.10)
(2.10)
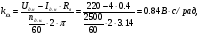 (2.11)
(2.11)
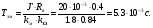
Запишем уравнение (2.9) в виде: 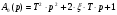 (2.12),
(2.12),
где 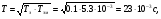 (2.13)
(2.13)
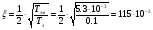 (2.14).
(2.14).
3. Построение желаемой ЛАЧХ.
Руководствуясь методикой, выбираем желаемую обратную ЛАЧХ 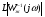 второго типа.
второго типа.
В нашем случае для коррекции ЭСП используются обратные связи по:
скорости, ускорению и моменту ИД. Также используется последовательное корректирующее устройство.
Применим общее корректирующее устройство во всех цепях обратных связей,тогда передаточная функция скорректированного разомкнутого ЭСП будет иметь вид:
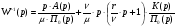 (3.1).
(3.1).
3.1. Нахождение рабочей точки.
Определение координат т. Ар исходя из требований по точности системы.
Найдём рабочую частоту:
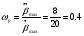 рад/с (3.1.1),
рад/с (3.1.1),
Расчитаем амплитуду гармонической составляющей управляющего воздействия:
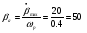 град (3.1.2),
град (3.1.2),
Пусть амплитуда гармонической составляющей ошибки будет равной 70% от заданной максимальной ошибки. Получим:
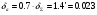 град (3.1.3).
град (3.1.3).
Ордината рабочей точки равна:
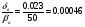 (3.1.4).
(3.1.4).
Таким образом, координаты рабочей точки Ар будут иметь значения:
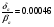 ;
; 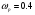 рад/с (3.1.5).
рад/с (3.1.5).
3.2. Построение ЛАЧХ.
Запишем уравнение передаточная функции неизменяемой части:
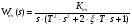 (3.2.1).
(3.2.1).
Используя найденные значения координат рабочей точки (3.1.5), строим 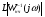 .
.
По построенному графику определим значение коэффициента усиления разомкнутой системы:
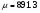 рад/с (3.2.2).
рад/с (3.2.2).
Из т. Ар проводим прямую с наклоном +40 дБ/дек до уровня – 13 дБ. Из полученной точки проводим прямую с наклоном +20 дБ/дек до пересечения с графиком 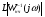 . Так как высокочастотная и низкочастотная асимптоты построенной ЛАЧХ и
. Так как высокочастотная и низкочастотная асимптоты построенной ЛАЧХ и 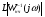 совпадают, то мы получили желаемую ЛАЧХ.
совпадают, то мы получили желаемую ЛАЧХ.
По построенному графику можем определить частоту среза системы:
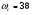 рад/с (3.2.3).
рад/с (3.2.3).
Пересечение 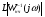 и
и 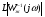 произошло в точке B, значение амплитуды в которой равно 13 дБ. Таким образом, система удовлетворяет требованиям по устойчивости и в введении последовательного корректирующего устройства нет необходимости:
произошло в точке B, значение амплитуды в которой равно 13 дБ. Таким образом, система удовлетворяет требованиям по устойчивости и в введении последовательного корректирующего устройства нет необходимости:
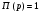 (3.2.4).
(3.2.4).
3.3. Расчет параллельного корректирующего устройства.
В общем виде обратную передаточную функцию системы, представленной на Схеме 1, можно представить в виде:
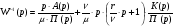 (3.1).
(3.1).
Второе слагаемое характеризует 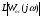 . Запишем передаточную функцию , применив к ЛАЧХ, изображенным на Графике 1 принцип сопоставления. Имеем:
. Запишем передаточную функцию , применив к ЛАЧХ, изображенным на Графике 1 принцип сопоставления. Имеем:
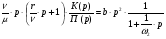 (3.3.1).
(3.3.1).
С целью упрощения реализации параллельного корректирующего устройства и улучшения параметров устойчивости проведем ЛАЧХ 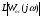 начиная с точки В под наклоном +40 дБ/дек. В этом случае имеем:
начиная с точки В под наклоном +40 дБ/дек. В этом случае имеем:
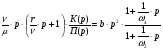 (3.3.2).
(3.3.2).
Потребуем, чтобы:
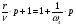 (3.3.3),
(3.3.3),
Тогда:
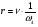 (3.3.4).
(3.3.4).
Исходя из (3.3.2), с учетом (3.2.4) получаем:
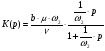 (3.3.5).
(3.3.5).
Потребуем, чтобы:
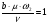
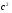 (3.3.6),
(3.3.6),
где b = 0.00275 – найдено из построений на Графике 1.
Откуда:
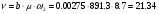 ед. (3.3.7).
ед. (3.3.7).
С учетом (3.3.7) и (3.3.4) получим:
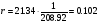 с (3.3.8).
с (3.3.8).
Итак, передаточная функция параллельного корректирующего устройства имеет вид:
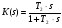 (3.3.9),
(3.3.9),
где 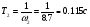 .
.
3.4. Техническая реализация параллельного корректирующего устройства.
Реализуем корректирующее устройство на основе RC-цепочки. По найденному значению передаточной функции подберем соответствующую RC-цепочку.
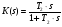 (3.3.9).
(3.3.9).
Выберем RC-цепочку следующего вида:
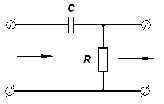
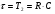 (3.4.1).
(3.4.1).
Пусть 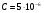 Ф = 5мкФ, тогда:
Ф = 5мкФ, тогда:
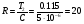 кОм.
кОм.
3.5. Проверка устойчивости внутреннего контура.
Необходимо проверить устойчивость контура местной обратной связи:
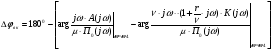 (3.5.1),
(3.5.1),
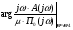 = + 900 + 2·760 = + 2420,
= + 900 + 2·760 = + 2420,
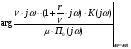 = + 2·900 – 890 + 450 = + 1360.
= + 2·900 – 890 + 450 = + 1360.
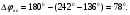
Запас устойчивости внутреннего контура больше 300, что благоприятно сказывается на устойчивости системы.
3.6. Проверка устойчивости всей системы.
Найдём запас устойчивости всей системы:
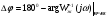 (3.6.1),
(3.6.1),
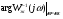 = + 900 + 900 – 750 + 2·100 = 1250,
= + 900 + 900 – 750 + 2·100 = 1250,
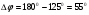 .
.
Запас устойчивости всей системы удовлетворяет требованиям по устойчивости.
4. Аналоговая САР с возмущающим воздействием.
Пусть нагрузка присоединена к ИД через редуктор.
Тогда уравнение (2.8) можно представить в виде:
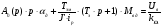 (4. 1)
(4. 1)
где 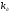 - коэффициент усиления двигателя
- коэффициент усиления двигателя 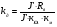
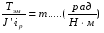 - коэффициент усиления момента
- коэффициент усиления момента
Составим уравнение системы в соответствии ос структурной схемой (см. схема 1):
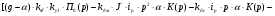
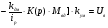 (4. 2)
(4. 2)
где 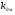 - коэффициент усиления датчика момента
- коэффициент усиления датчика момента
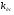 - коэффициент усиления датчика скорости
- коэффициент усиления датчика скорости
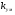 - коэффициент усиления усилителя мощности
- коэффициент усиления усилителя мощности
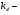 коэффициент усиления ВТ
коэффициент усиления ВТ
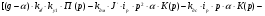
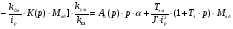 (4. 3)
(4. 3)
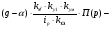
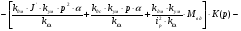
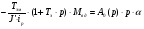 (4. 4)
(4. 4)
Обозначим:
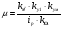 - коэффициент усиления разомкнутой системы (4. 5)
- коэффициент усиления разомкнутой системы (4. 5)
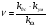 - коэффициент усиления разомкнутого внутреннего контура (4. 6)
- коэффициент усиления разомкнутого внутреннего контура (4. 6)
связи по скорости
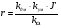 - коэффициент усиления разомкнутого внутреннего контура
- коэффициент усиления разомкнутого внутреннего контура
связи по моменту, развиваемому ИД (4. 7)
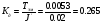 (4. 1)
(4. 1)
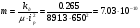 - коэффициент усиления системы по моменту (4. 8)
- коэффициент усиления системы по моменту (4. 8)
С учетом введенных обозначений получим:
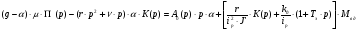
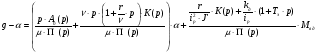 (4. 9)
(4. 9)
Положим 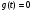 , тогда:
, тогда:
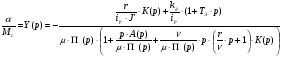 (4. 10)
(4. 10)
Введем обозначение: 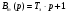 , тогда:
, тогда:
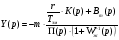 (4. 11)
(4. 11)
ЛАЧХ передаточной функции по возмущающему воздействию представлен на графике 2.
Рассчитаем ошибку САР при возмущающем воздействии:
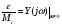
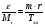
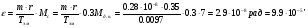 . (4. 12)
. (4. 12)
Расчетная ошибка САР оказалась меньше заданной (3’).
Рассчитаем ошибку САР при возмущающем воздействии в точке с частотой 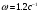 :
:
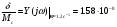 (4. 13)
(4. 13)
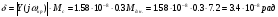 (4. 14)
(4. 14)
Расчетная ошибка САР в критической точке оказалась меньше заданной (3’), поэтому введение связи по возмущающему моменту не является необходимым и будет рассматриваться далее не более как учебная.
Определим основные коэффициенты:
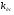 = 1.3
= 1.3
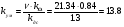 (4. 15)
(4. 15)
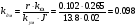 (4. 16)
(4. 16)
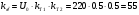 (4. 17)
(4. 17)
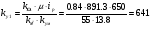 (4. 18)
(4. 18)
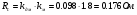 (4. 19)
(4. 19)
Расчетная ошибка САР в критической точке оказалась меньше заданной (2’), поэтому введение связи по возмущающему моменту не является необходимым.
5. Введение связи по возмущающему воздействию.
Введем связь по возмущающему воздействию в учебных целях. Введение связи по возмущающему воздействию позволяет существенно уменьшить моментальную составляющую ошибки. Структурная связь при введении связи по возмущающему воздействию показана на Схеме 2.
Запишем уравнение для САР:
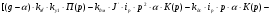
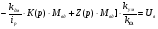
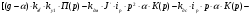
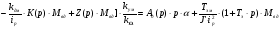
Аналогично, как и для Y(p) проведя замены, получим:
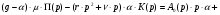
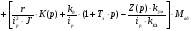
Так как моментная составляющая желательно должна быть сведена к нулю, получаем:
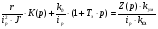
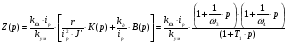
Введем обозначение: 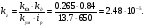
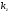 - коэффициент усиления корректирующего устройства
- коэффициент усиления корректирующего устройства
Для упрощения реализации корректирующего устройства будем считать, что оно должно работать при частотах 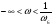 , тогда:
, тогда:
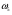 = 0.05
= 0.05
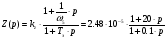 (5.5).
(5.5).
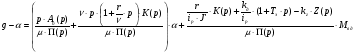
Положим 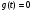 , тогда:
, тогда:
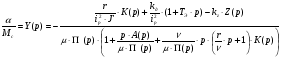
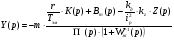
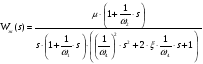
ЧАСТЬ 2
Техническое задание.
Спроектировать следящую САУ, согласно Схеме 1 (Часть 1), в соответствии с параметрами, представленными в Техническом задании (Часть 1) и следующими требованиями к переходному процессу:
Перерегулирование:
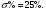
Время переходного процесса:
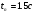 .
.
Угол отработки ступени:
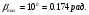
2. Построение желаемой ЛАЧХ.
Рабочая точка имеет те же координаты, что и в Части 1. Найдём левую границу частоты среза 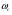 по графикам зависимости
по графикам зависимости 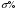 , Тп от Рmax. Для
, Тп от Рmax. Для 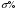 = 25% имеем:
= 25% имеем:
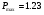 (2.1),
(2.1),
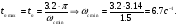 (2.2).
(2.2).
Найдём правую границу частоты среза 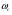 :
:
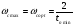 (2.3),
(2.3),
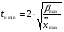 (2.4),
(2.4),
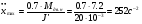 (2.5).
(2.5).
В соответствии с (2.4) имеем:

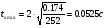 (2.6).
(2.6).
Окончательно получаем:
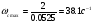 . (2.7).
. (2.7).
Через рабочую точку проводим прямую под наклоном +60дБ/дек до уровня –Lм = -16 дБ (найдено по номограмме). Из этой точки проводим среднечастотную асимптоту под наклоном +20дБ/дек до пересечения с ЛАЧХ неизменяемой части. См. График 1. В ходе построения получили:
b = 0.0076 (2.8),
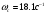 (2.9.).
(2.9.).
Полученное значение частоты среза удовлетворяет условию:
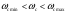 (2.10).
(2.10).
Пересечение 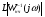 и
и 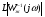 произошло в точке B, значение амплитуды в которой достаточно, чтобы система удовлетворяла требованиям по устойчивости и в введении последовательного корректирующего устройства нет необходимости:
произошло в точке B, значение амплитуды в которой достаточно, чтобы система удовлетворяла требованиям по устойчивости и в введении последовательного корректирующего устройства нет необходимости:
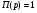 (2.11).
(2.11).
3. Расчет параллельного корректирующего устройства.
Расчет параллельного корректирующего устройства будем производить теми же методами, что в Части 1.
С целью упрощения реализации параллельного корректирующего устройства и улучшения параметров устойчивости проведем ЛАЧХ 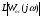 начиная с точки В под наклоном +40 дБ/дек. В этом случае имеем:
начиная с точки В под наклоном +40 дБ/дек. В этом случае имеем:
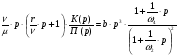 (3.1).
(3.1).
Потребуем, чтобы:
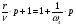 (3.2),
(3.2),
Тогда:
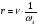 с. (3.3).
с. (3.3).
Исходя из (3.1), с учетом (3.2) получаем:
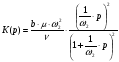 (3.4).
(3.4).
Потребуем, чтобы:
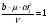 (3.5),
(3.5),
Откуда:
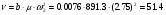 (3.6).
(3.6).
С учетом (3.3) и (3.6) получим:
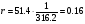 с. (3.7).
с. (3.7).
Передаточная функция параллельного корректирующего устройства имеет вид:
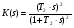 (3.8),
(3.8),
где 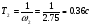 .
.
4 Техническая реализация параллельного корректирующего устройства.
Реализовывать корректирующее устройство будем посредством последовательного соединения двух RC-цепочек.
Постоянная времени будет меняться за счёт С.
Схема RC-цепочек:
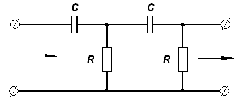
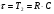 (4.1).
(4.1).
Пусть 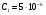 Ф = 5мкФ, тогда:
Ф = 5мкФ, тогда: 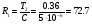 кОм.
кОм.
Тогда 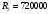 Ом. =
Ом. = 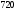 кОм.
кОм.
Рассчитаем 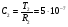 Ф.
Ф.
5. Проверка устойчивости внутреннего контура.
Проверка устойчивости контура местной обратной связи:
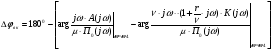 (5.1),
(5.1),
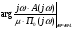 = + 900 + 2·760 = + 2420,
= + 900 + 2·760 = + 2420,
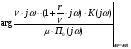 = + 3·900 – 2·900 + 450 = + 1350.
= + 3·900 – 2·900 + 450 = + 1350.
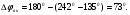
Запас устойчивости внутреннего контура больше 300, что благоприятно сказывается на устойчивости системы.
6. Проверка устойчивости всей системы.
Определим запас устойчивости всей системы:
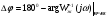 (6.1),
(6.1),
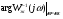 = + 900 +2· 900 – 2·800 + 2·30 = 1160,
= + 900 +2· 900 – 2·800 + 2·30 = 1160,
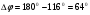 .
.
Запас устойчивости всей системы удовлетворяет требованиям по устойчивости.
7. Переходной процесс САУ.
Найдем переходный процесс САР при подаче на вход управляющего воздействия 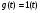 .
.
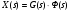 (7.1),
(7.1),
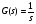 (7.2),
(7.2),
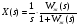 (7.3).
(7.3).
Передаточную функцию 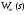 находим исходя из построенной ЛАЧХ (см. График 1):
находим исходя из построенной ЛАЧХ (см. График 1):
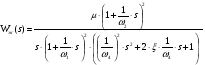 (7.4).
(7.4).
Переходной процесс находим с использованием программы MatLab 6.5 (см. График 2).
Перерегулирование будет составлять:
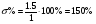 (7.5).
(7.5).
Время переходного процесса:
tп = 0.3 c (7.6).
8. Расчет коэффициентов усиления устройств, входящих в САУ.
Получим коэффициенты усиления устройств, входящих САУ.
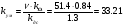
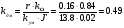
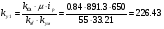
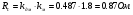
Часть 3.
Введение нелинейности.
Нелинейный элемент введем перед Ку1.
Вводимая в систему нелинейность имеет вид:
X2
X1
c
-c
b=-a/b
b=a/b
b=1
a=45 град.
Уравнение нелинейности в общем виде:
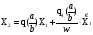
Данный нелинейный элемент не имеет петли гистерезиса, следовательно 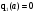
Для данной нелинейности:
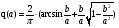
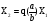
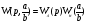
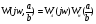
Исследуем систему на наличие предельных циклов, и, в случае их существования исследуем каждый на устойчивость.
Условие нахождения системы на границе устойчивости:
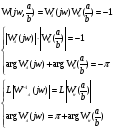
Так как 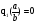 , то
, то 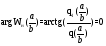
Запишем условие существования в САР предельных циклов:
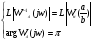
Графики 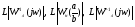 представлены в приложении.
представлены в приложении.
В данной системе 2 предельных цикла со следующими параметрами:
1. 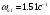
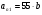
2. 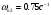
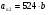
Предельный цикл будет устойчив, если при 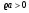 ЛФЧХ линейной части системы
ЛФЧХ линейной части системы
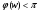 , а при
, а при 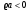 -
- 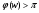 .
.
В нашем случае устойчивым является первый цикл с параметрами:
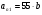

Нравится материал? Поддержи автора!
Ещё документы из категории разное:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ