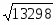
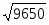
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕСИОНАЛЬНОГО ОБРАЗОВАНИЯ СВЕРДЛОВСКОЙ ОБЛАСТИ

Управление образования Администрации г. Екатеринбурга

МОУ – Гимназия № 45

Ансамбль пирамид в Гизе – кладезь математических знаний.

Научный проект по геометрии

Исполнители:

Кадачигова Юлия,

ученица 11 «А» класса

Иванов Алексей

ученик 11 «А» класса

Гимназии №45

Руководитель:

учитель Высшей категории

Бердникова Т.В.

г. Екатеринбург

2008 г.

Содержание:

Введение. 3

1. Ансамбль пирамид в Гизе. 4-6

1.2 Диагональные пропорции пирамид. 6-7

2. Пирамида Хафра. 8-9

3. Египетский Треугольник. 10-13

4. Составные треугольники. 14-16

4.1 Единая формула для составления

основного- результирующего угла. 17-21

5. Знания в области математики и арифметики Древнего Вавилона. 22-25

6. Практическая часть «Записки программиста» 26

6.1 Алгоритм 26-28

6.2 Язык программирования 28

6.3 Интерфейс 29

6.4 Листинг 29-34

Заключение. 35

Список литературы. 36

Введение

На сегодняшний день человеку известно очень многое о величии древних пирамид. Этой теме посвящено не мало изданий. Нам тоже стала интересна эта тема, и рассмотрение ее в ранее не изведанной области, которую автор одной из книг назвал «Пирамидометрия».

Фактически, мы впервые прикоснулись к древнейшему архиву математики, зафиксированному в форме пирамид, основываясь на широко известных и мало известных свойствах чисел и геометрических форм. Пирамиды являются не только притягательными сооружениями, но и интеллектуальными посланиями из глубины тысячелетий, сокровищницами системы красивейших математических законов. За всю историю наука не знала подобных примеров мудрости, исходящей от наших предшественников.

Поэтому мы поставили для себя следующие задачи:

1. Узнать максимально о фигуре в форме четырехугольной пирамиды и выяснить, почему такой почет отдан именно этой фигуре. Какая геометрическая суть вкладывалась в пропорции столь грандиозных объектов?

2. Разобраться в особенностях египетского треугольника и единой формуле для трех сторон результирующего прямоугольного треугольника.

3. Создать на основе исследованного материала собственную математическую программу.

Мы решили углубиться в эту тему с научной точки зрения, а именно, рассмотреть строение пирамид.

1. Ансамбль пирамид в Гизе

Пирамида – это многогранник, одной из граней которого служит многоугольник. В зависимости от числа боковых граней пирамиды делятся на треугольные, четырехугольные и т.д.

История древних цивилизаций немыслима без фигур в форме четырехугольной пирамиды. В течение столетий с непостижимым упорством возводились целые горы из камня в виде пирамид. Следы этих сооружений находят в местах, отстоящих друг от друга на тысячи километров. Всем известны наиболее сохранившиеся пирамиды в Египте и, в частности, на плато Гизе( на западном берегу великой реки Нил).

Так почему такой почет именно этой фигуре и какая геометрическая суть вкладывалась в пропорции столь грандиозных объектов?

Вопрос не нов, и спектр ответов широк, особенно в отношении Великой пирамиды (пирамиды Хеопса или Хуфу).

Так, одной из загадок Великой египетской цивилизации считается совершенно точное вычисление объема усеченной пирамиды с квадратным основанием:

V=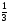(a² +ab +b²)h,

где a и b – длины сторон оснований, h – высота.

Но еще более феноменальным является то, что при внимательном рассмотрении закономерностей в пропорциях теоретической модели Великой пирамиды, именно в ней, мы находим небывалый источник информации о свойствах коэффициента золотого сечения и в его различных комбинациях. Фактически мы имеем объемную фигуру, которая является неиссякаемым генератором чудесных отношений.

Ансамбль пирамид в Гизе, относящийся ко времени IV династии, скомпонован в единую группу. Все пирамиды довольно точно расположены по странам света почти параллельно одна другой. Трудность точного измерения пирамид (почти полное разрушение облицовки и непостоянный уровень песка) приводит к сильно различающимся у разных авторов размерам (так, высота пирамиды Хеопса указывается в отдельных случаях с разницей в 2 м). Поэтому при анализе пропорций здесь необходима особая осторожность.

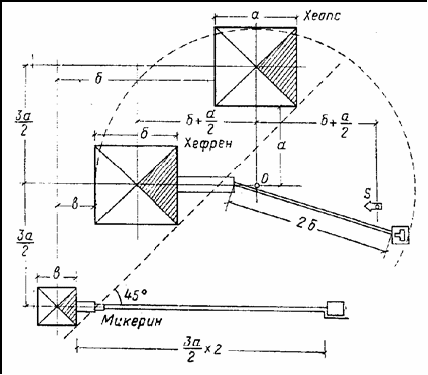
В построении общего плана ансамбля наблюдаются простые отношения: равенства и половины. Так, расстояние от угла пирамиды Хеопса до центра пирамиды Хефрена, находящегося почти на продолжении диагонали пирамиды Хеопса, равно этой диагонали.

Если провести координаты, параллельные сторонам (и странам света), через центры всех трех пирамид ансамбля, то окажется, что по линии север–юг расстояния между центрами пирамид одинаковы, причем эти расстояния равны 3/2 стороны пирамиды Хеопса.

Центр каждой следующей пирамиды по горизонтальной координате отстоит от основания предыдущей на расстоянии, равном стороне своего собственного основания (с очень небольшой неточностью).

Как меньшая, пирамида Микерина

выдвинута вперед по координате запад–восток, так что юго-восточные углы всех трех пирамид находятся почти на одной прямой.

рис. 1. Пропорции пирамид в Гизе.

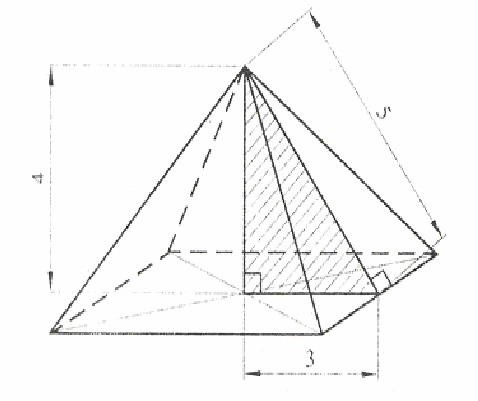
Пропорции пирамид в Гизе близки между собой. Разрезы всех пирамид дают приблизительно одинаковое отношение высоты к стороне основания и сходный угол наклона 2 боковых сторон, равный у пирамиды Хеопса 51°20′, у пирамиды Хефрена 50°20′ и у пирамиды Микерина 51°. Высота и сторона основания пирамиды Хеопса — 146.59 и 230.35 м, а по другим данным — 148.2 и 232.8 м, Хефрена — 143.5 и 215.25 м; Микерина — 66.4 и 108.04 м.

В пирамиде Хефрена отношение высоты к стороне основания составляет 2 : 3, причем эта пропорция выдержана математически правильно:

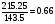
Поэтому разрез пирамиды Хефрена может быть построен из двух сложенных треугольников с отношением сторон 3 : 4 : 5, где величина 4 соответствует высоте. При таком предположении пирамиду Хефрена можно считать самым ранним памятником, в котором проявляются пропорции египетского треугольника.

1.1 Диагональные пропорции пирамид в Гизе.

Все описанные пропорции обнаруживаются в поперечном разрезе пирамид. Однако более вероятным представляется следующий способ определения их пропорций. В папирусе Ринд, предположительно относимом к Древнему царству, есть задачи на построение пирамид. В них связываются три величины, относящиеся к диагональному сечению (разрезу) через пирамиду по противоположным ребрам: диагональ основания пирамиды, сторона ребра и угол между ними. Требуется по любым двум данным из этих трех величин найти третью.

Возможность решения этих задач позволяет сделать вывод, что построение пропорций пирамиды основывалось на диагональном сечении. В простейшем случае это построение можно представить себе таким образом: если мы разрежем квадрат по диагонали и половину его загнем на вертикальную плоскость, то получим диагональный разрез пирамиды, для которой весь квадрат является основанием. Такой идеальный случай не встречается при построении пирамид (везде их высота меньше половины диагонали основания), но все же они могли быть построены по тому же методу.

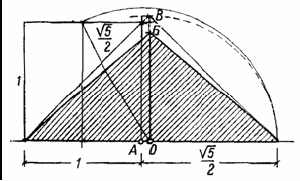
Пирамида Хефрена построена по производным квадрата. Но диагональ его половины засечена от края квадрата, а не от середины. Из средней точки основания пирамиды О восстановлен перпендикуляр, определяющий вершину пирамиды (Б — на продолжении верхней горизонтали квадрата) и угол плана (В — на продолжении диагонали квадрата или в точке пересечения перпендикуляра с полуокружностью). Заштрихованный внутренний треугольник является диагональным разрезом пирамиды. Те же результаты могут быть получены следующим построением. Из крайней точки А исходного квадрата радиусом, равным половине диагонали полуквадрата, засекается крайняя точка Б диагонали пирамиды. Радиусом ОБ описывается полуокружность до точки В. Соединение точек Б и В с точками Г и Д определит половину основания и диагональный разрез пирамиды. При указанных построениях получается отношение высоты разреза к основанию:

1+ 1.118=2.118(Основание)

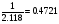
Реальная величина этого отношения в пирамиде Хефрена (при стороне в 215.25 м,

высоте 143.50 м и вычисленной диагонали 304.36 м) будет:

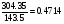(отклонение на 0.0007, много меньше допустимого).

Эта величина соответствует малой функции золотого сечения.

Важная роль отношения 0.472 для построения пирамиды Хефрена подтверждается тем, что то же отношение определяет основные пропорции плана преддверия храма при пирамиде Хефрена, выдвинутого вперед.

рис.2

2. Пирамида Хафра.

Хотя пирамида Хафры и уступает размерами пирамиде его отца Хуфу, её положение на более высоком холме и её более крутой склон делают её достойной соперницей Великой Пирамиды. Две довольно большие камеры и два перекрещивающихся прохода, которые ведут в горизонтальный коридор, представляют собой довольно скромное по отношению к пирамиде Хуфу пространство. Кровлю камеры обеспечивал свод на стропилах, расцененный как более прочный, чем горизонтальные ригели пирамиды Хуфу. Ниша для каноп, размещенная около саркофага Хафра, была новшеством, которое станет распространенным в более позднее время. Ныне эта пирамида находится в хорошем состоянии, хотя её размеры несколько уменьшились, и составляют на сегодняшний день основание - 210,5 × 210,5 м и высота - 136,5 м.

Пирамида Хафра была всего лишь элементом заупокойного комплекса, который включал в себя маленькую пирамиду-спутницу, вероятно построенную для супруги Хафра, стену ограждения, заупокойный храм, дорогу, храм в долине и порт, который также необходимо было построить. Современное состояние сохранности комплекса позволяет сказать, что все его элементы были завершены. Храмы Хафры, ставшие образцами для фараонов Древнего царства, были построены из многотонных блоков гранита и известняка. Каменные блоки у входа в его заупокойный храм достигают в длину 5,45 м и весят до 42 тонн. Это были обширные здания: 113 м на 49 м — заупокойный храм, и 45 м на 50 м — храм в долине, сохранившаяся высота которого в настоящее время составляет 13 м. Учитывая найденные фрагменты, общее количество скульптурных произведений нижнего храма Хафра насчитывает более 200 статуй.

Наличие в теоретической модели этой пирамиды «египетского» треугольника со сторонами 3:4:5 достаточно очевидно и особых разногласий на сей счет у специалистов не возникает. Но дальнейший анализ закономерностей такой платформы пирамиды остается вне сферы внимания у архитекторов, математиков и историков. Поэтому возьмем соотношение элементов пирамиды за основу и выясним математические особенности модели пирамиды Хафра.

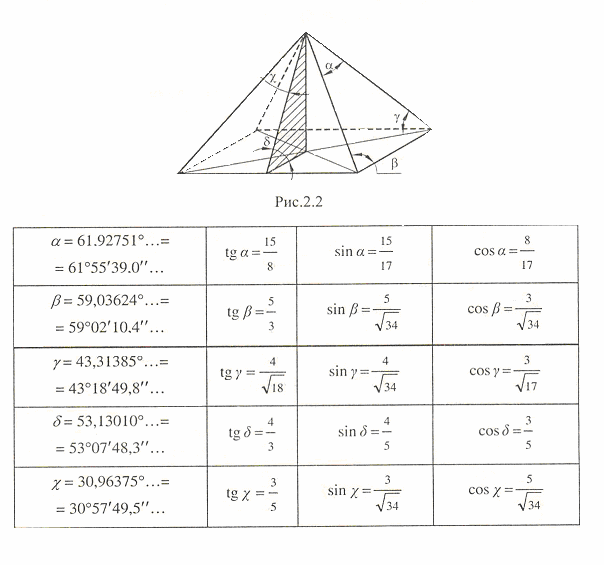
Значения основных углов пирамиды Хафра.

На фоне иррациональных значений углов, выраженных в градусной мере, выглядит вполне лаконичной и, главное, предельно точной их запись в тригонометрической форме. Иначе говоря, такие углы входят в состав соответствующих треугольников со сравнительно простым соотношением сторон.

Как можно заметить, математическая модель пирамиды Хафра особенно наглядно демонстрирует целый комплекс оригинальных взаимоотношений целых чисел или рациональных дробей, но не без участия и иррациональных, посредством взаимного проникновения прямоугольных треугольников. Получается что формулу этой модели пирамиды определяют три целочисленных треугольника со сторонами 3:4:5, 8:15:17, 7:24:25.

3.Египетский треугольник

Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.

Особенностью такого треугольника, известной ещё со времён античности, является то, что при таком отношении сторон теорема Пифагора даёт целые квадраты как катетов, так и гипотенузы, то есть 9:16:25. Египетский треугольник является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.

Название треугольнику с таким отношением сторон дали эллины: в VII - V веках до н. э. греческие философы и общественные деятели активно посещали Египет. Так, например, Пифагор в 535 до н. э. по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к формулировке и доказательству его знаменитой теоремы.

Египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов землемерами и архитекторами.

Для построения прямого угла использовался шнур или верёвка, разделённая отметками (узлами) на 12 (3+4+5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры-катеты являлись направляющими для кладки прямого угла сооружения.

В архитектуре средних веков египетский треугольник применялся для построения схем пропорциональности.

Любой треугольник можно построить геометрическим способом, если известна длина всех трех сторон и длина двух сторон и угол между ними, если задано соотношение сторон треугольника. Последнее действительно задано как 3 : 4 : 5

Для доказательства теоремы о египетском треугольнике необходимо использовать отрезок прямой известной длины А-А1.Он будет служить масштабом, единицей измерения, и позволит определить длину всех сторон треугольника. Три отрезка А-А1 равны по длине наименьшей из сторон треугольника ВС, у которой соотношение равно 3. А четыре отрезка А-А1 равны по длине второй стороне, у которой соотношение выражается числом 4. И, наконец, длина третьей стороны равна пяти отрезкам А-А1. Проведем отрезок ВС, являющийся наименьшей стороной треугольника. Затем из точки В радиусом, равным отрезку с соотношением 5, проводим циркулем дугу окружности, а из точки С —дугу окружности радиусом, равным длине отрезка с соотношением 4. Если теперь точку пересечения дуг соединить линиями с точками В и С, то получим прямоугольный треугольнике соотношением сторон 3 : 4 : 5. Что и требовалось доказать.

3 + 5 = 8. а число 4 составляет половину числа 8. Числа 3, 5, 8 имеют прямое отношение к золотому сечению и входят в так называемый «золотой ряд»: 1, 1, 2, 3, 5, 8, 13, 21... В этом ряду каждый последующий член равен сумме двух предыдущих: 1 + 1= 2. 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8 и так далее.

Выражение «золотое сечение» впервые ввел в XV веке Леонардо да Винчи. Но сам «золотой ряд» стал известен в 1202 году, когда его впервые опубликовал в своей «Книге о счете» итальянский математик Леонардо Пизанский. прозванный Фибоначчи. Однако почти за две тысячи лет до них золотое сечение было известно Пифагору и его ученикам. Правда, называлось оно по-другому, как «деление в среднем и крайнем отношении». А вот египетский треугольник с его «золотым сечением» был известен еще в те далекие времена, когда строились пирамиды в Египте.

Так кому же принадлежит первенство в этих выдающихся знаниях? Ясно, что их корни скрываются в глубине тысячелетий или в просторах космоса. О золотом сечении «забыли» в средние века, когда инквизиторы в церковных мантиях в борьбе с новыми веяниями в науке мечом и огнем уничтожили многие знания и их носителей, среди которых было много выдающихся мыслителей и посвященных. Но о нем вспомнили в XIX веке. Позднее оно нашло широкое применение в архитектуре, искусстве, полиграфии, компьютерах и в других областях человеческой деятельности.

Когда говорят о золотом сечении, то чаще всего имеют в виду гармоничное соотношение высоты к ширине или соотношение последовательных отрезков, расположенных на одной прямой и находящихся в отношении друг к другу согласно «золотому» ряду чисел. Здание, в котором отношение высоты к ширине или отношение между высотами отдельных надстроек-этажей укладывается в «золотой» ряд, выглядит гармонично. Очевидно, все в мире подчиняется золотому правилу. И всякое искусственное его нарушение приводит к искажению законов природы и космоса, вносят дисгармонию в окружающее пространство.

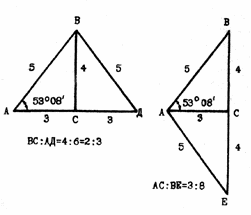
А как же египетский треугольник? Ведь у него отношение катетов, то есть «ширины» к высоте, составляет 3:4 и как бы выпадает из «золотого» ряда чисел? Но так ли это? Пристроим к египетскому треугольнику АВС (рис.3) равный ему треугольник ВСД так, чтобы катет ВС, в цифровом

выражении равный 4, был общим. Получим равнобедренный треугольник АВД. В нем

рис.3

отношение высоты к основанию ВС : АД = 4:6 = 2:3. соотношение 2:3 — из «золотого» ряда.

Посмотрим теперь другой параметр: отношение высоты к боковой стороне: ВС : АВ = ВС : ВД = 4:5. Подобное соотношение применялось в прошлом и применяется в наше время в прикладных искусствах. В древние времена оно находило применение в архитектуре.

А теперь пристроим к египетскому треугольнику АВС равный ему треугольник АСЕ так, чтобы уже другой катет АС стал общим для них. Получим равнобедренный треугольник АВЕ, в котором отношение высоты к основанию АС : ВЕ = 3:8. Числа 3 и 8 тоже из «золотого» ряда, но они не являются соседними в ряду. Оказывается, это не служит препятствием для создания гармоничной пропорции. Более того, пропорция, образованная этим равнобедренным треугольником, где АС : ВЕ = 3 : 8. по мнению некоторых специалистов, в частности Р. Энгель-Гардта (1919 г.), дает «чудесную гармонию». Таким образом, получается, что египетский треугольник прямо и косвенно связан с золотым сечением.

Слева - "пирамида" в которой соотношение высоты к основанию ВС:АД = 4 : 6 = 2 : 3 - удовлетворяет пропорции золотого ряда чисел. Справа - равнобедренный треугольник у которого соотношение высоты к основанию АС:ВЕ = 3 : 8 также образует гармоническую пропорцию

.

рис.4

4. Составные треугольники.

В следующей части своей работы я выяснила, какие существуют потенциальные возможности составных треугольников( основополагающих схем).

Обратимся к схеме прямоугольного треугольника, где суммируются два различных угла. Для этого в качестве исходного примера возьмем сумму двух треугольников из пирамиды Хафра (Хефрена), имеющих стороны 3;4;5 и 3;5;.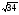

Рис.5

Рис.6. Пирамида Хафра и определяющий её параметры египетский треугольник

В результате рассмотрения закономерностей такого примера и применений соответствующих навыков, а так же пользуясь уже приведенными данными автора одной из книг, можно получить более общую параметрическую схему прямоугольного треугольника. Появляется возможность рассмотреть свойства прямоугольного треугольника изнутри – через универсальный безразмерный параметр.

Рис.7. Параметрическая структурная схема прямоугольного треугольника с демонстрацией принципа взаимодействия ( суммирования) двух углов.

Из рис.7 имеем:

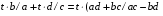
где 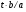- тангенсная мера угла 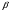; 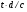-тангенсная мера угла 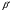; 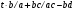-тангенсная мера угла (+) .

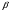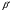Углы 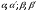связаны следующей зависимостью:

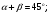
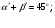
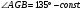
Далее можно добавить :

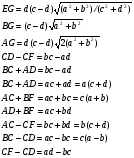
Все эти действия позволяют достаточно легко и наглядно манипулировать отрезками, содержащими в своей основе числа a,b,c, и d.

Таким образом на основании структурной схемы, показанной на рисунке 7, мы можем суммировать различные углы, заданные любыми безразмерными отношениями, такими как синусное, косинусное, тангенсное и котангенсное, и получать ответы так же в любых безразмерных отношениях через стороны результатирующего треугольника. Например:

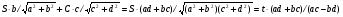
где 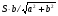– синусная мера угла 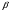; 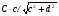– косинусная мера угла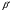; 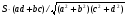- синусная мера угла(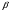+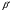); 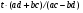- косинусная мера угла(+).

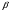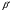4.1 Единая формула для трех сторон составного – результатирующего угла прямоугольного треугольника.

Все многообразие схем по суммированию одинаковых углов объединяется единой формулой для трех сторон составного – результатирующего прямоугольного треугольника.

То есть для суммы n равных углов в рамках прямоугольного треугольника будем иметь следующую зависимость в декартовой системе координат (см.рис.8 )

Рис.8.

При возведении сторон прямоугольного треугольника в квадрат получим формулу:

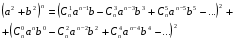(1)

Где 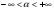-прилежащий катет коренного угла 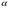, 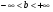- противолежащий катет коренного угла 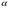, 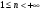- целое количеств углов в искомой сумме; 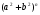- квадрат гипотенузы составного – результатирующего треугольника.

Многочлены в скобках обрываются сами собой, заканчиваясь слагаемым с нулевой или первой степенью числа a. При n= 1 получим уравнение Пифагора.

Известна формула бинома Ньютона:

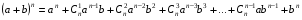(2)

Где n- целое положительное число.

На рисунке 8 имеется гипотенуза, квадрат которой можно разложить аналогичным образом:

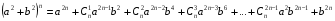(3)

Тогда формула (1) примет следующий вид:

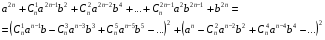
В тангенсной мере формула суммы n-углов примет вид :

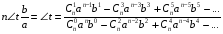
При рассмотрении общей закономерности на рис.8 Имеют место частные случаи, когда а=0 или b=0 в параметрах исходного коренного угла, а так же na= 0^о, na=90^о, na=180^о, и т.д. в параметрах результатирующего угла.

То есть имеют место равенства:

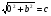или 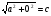, значит a=c или b=c, а также

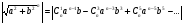(4)

или

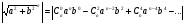(5)

Пример

Возьмем угол 90^о у которого прилежащий катет равен 0^о, а противолежащий равен числу b. Определить его тройное и учетверенное значение.

Решение

1)Гипотенуза у результатирующего треугольника примет значение для тройного угла:

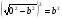
Противолежащий катет должен быть равен:

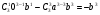
Это возможно при условии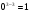

Прилежащий катет равен: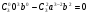

Результат соответствует углу 270^о и формуле (4)

2)гипотенуза результатирующего треугольника с учетверенным углом будет равна:

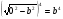
Противолежащий катет будет равен:

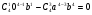
Прилежащий катет должен быть равен:

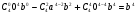
Это возможно при условии 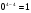. Тогда результату соответствует углу 360^о и формуле (5)

Используя принцип сложения углов, показанный на рисунке можно получат суммы трех, четырех, пяти и т.д. различных углов.

В тангенсной мере для трех суммирующих углов это будет выглядеть так:

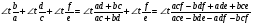
Где b/a; d/c; f/e – противолежащий и прилежащий катеты соответствующих углов.

Для пяти различных углов формула примет следующий вид:

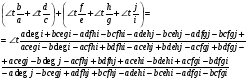
Где b/a, d/c, f/e, h/g, j/I – противолежащий и прилежащий катеты соответствующих углов.

При надобности можно вывести и тригонометрические формулы суммы любого количества углов. Параметрические структурные схемы примечательны еще тем, что они прекрасно иллюстрируют действия с комплексными числами

Рис.9 Упрощенная структурная схема, демонстрирующая адекватность действий сложения двух различных комплексных чисел. На схеме буква i маркирует отрезок демонстрирующий чисто минимумную часть комплексного числа.

а, с – действительные числа.b,d – числа без мнимой единицы, bi, di – чисто мнимые числа; z₁ = a+ bi, z₂ = c+di – комплексные числа; z₁ = a- bi z₂ = c-di - сопряженные числа.

Из элементарной математики известно, что произведение двух комплексных чисел имеет вид : (a+bi)( c+di) = ( ac-bd)+(ad+bc)i. т.е имеем полное соответствие катетам коренных и результатирующего треугольников.

Формула возведения в степень комплексного числа:

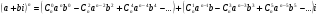
Формулой открывается ряд свойств комплексных чисел и ряд свойств групп членов биноминального разложения.

Конечно, начальное знакомство с открывающимися закономерностями не позволяет делать какие – либо окончательные выводы, но такая спрессованность материала в столь известных и древних объектах поражает.

5. Знания в области алгебры и арифметики Древнего Вавилона.

В статье В.Макарова и В.Морозова «В лучах кристалла Земли» из журнала «Техника молодежи» рассматривается гипотеза о икосаэдро-додекаэдрической сруктуре земли.

Икосаэдр и додекаэдр вписаны в земной шар таким образом, что на поверхности Земли, на ребрах и вершинах этих фигур, располагаются геофизические, биосферные и атмосферные аномалии. А в районе вершин таких тел сконцентрированы очаги наиболее крупных развитых культур и цивилизации древнего мира.

Примечательно, что в устных и письменных источниках есть упоминание о каком-то треугольном делении Земли. Археологами найдены «странные предметы» в виде додекаэдра. В вершинах додекаэдра сферические выпуклости, а в центрах граней - отверстия. Отсюда возникло предположение, что «странный предмет» - это модель силовой системы Земли.

По современным представлениям, подобную ячеистую галактику имеют и скопления галактик окружающего нас макромира.

В упомянутой статье очень красивой выглядит идея о существовании в центре Земли управляющего твердого тела в форме додекаэдра.

Современная история математики доказывает, что Древний Вавилон использовал куда более солидные познания в математике, чем древний Египет.

Так, в книге Б.Л.Ван дер Вардена «Пробуждающаяся наука математика Древнего Египта, Вавилона и Греции» имеется такое заключение о знаниях в области алгебры и арифметики Древнего Вавилона:

«Нормальные формы, которые вавилоняне могли легко решать и к которым они старались сводить все алгебраические уравнения, были таковы:

А.Уравнения с одним неизвестным:

ax=b,

x2=a,

x2=ax=b,

x2-ax=b,

x3=b.

x2(x+1)=a/

В.Системы уравнений с двумя неизвестными:

x+y=a, xy=b,

x-y=a, xy=b,

x+y=a, x2+y2=b,

x-y=a, x2+y2=b,

Кроме того, были известны формулы:

(a+b)2=a2+2ab+b2

(a+b)(a-b)=a2-b2

1+2+4+…+2h=2h+(2h-1)

12+22+32+…+n2=(1/3+2n/3)(1+2+3=…n)

и суммирование арифметических прогрессий.

Пифагоровы числа x2+y2=z2 находились при помощи формул:

x= p²-q²

y=2pq

z=p²+q²

Такое совпадение знаний вавилонян в области алгебры с конкретными графическими схемами, исходящими от древнейших пирамид, указывает на наличие единого источника просвещения для различных времен и народов.

В Плимтоновской библиотеке Колумбийского университета в Нью-Йорке имеется замечательный древневавилонский клинописный текст «Plimpton 322» , которому порядка 4000 лет. В нем имеются столбцы цифр, которые указывают на умение мудрецов определять целочисленные тройки – стороны прямоугольных треугольников. В современном исчислении они выглядят следующим образом ( таблица 1). Сейчас мы можем определить для этих троек коренные пары чисел (катеты) в составе половины углов. После чего намечается определенная градация этих примеров даже на таком небольшом фрагменте некогда существовавших математических знаний.

№строки

Тройки чисел согласно Б.Л.Ван дер Вардену

Родственные тройки чисел – исходные для результатирующего угла.

Примечание

Катеты разной четности и гипотенуза

Катеты нечетные и гипотенуза

1

120,119,169

15, 12,13

7,17,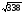

2

346,3367,4825

27, 64,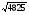

37,91,

3

4800,4601, 6649

32, 75,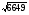

43,107,

4

13500, 12709, 18541

54, 125,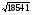

71,179,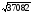

5

72,65,97

4,9,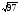

5,13,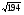

6

360,319, 481

9,20,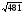

11,29,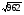

7

2700,2291, 3541

25,54,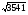

29,79,

8

960, 799,1249

15,32,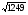

17,47,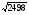

9

600, 481,769

12,25,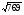

13,37,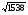

10

6480, 4961, 8161

40,81,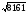

41,121,

11

60,45,75

1,2,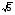

1,3,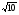

Исходная тройка чисел не является примитивной

12

2400, 1679, 2929

25,48,

23,73,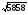

13

240, 161,289

8,15,17

7,23,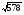

14

2700,1771,3229

27,50,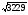

23,77,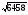

15

90, 56, 106

90,56,106

5, 9,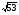

В некоторых случаях можно поменять местами коренные тройки, исходная тройка чисел не является примитивной

При первом просмотре результатов таблицы 4 можно сделать предварительные замечания:

- результат отношения катетов из столбца для пар чисел разной четности возрастает от 0, 41666… в первой строке, до 0,54 в четырнадцатой. Соответственно убывает отношение катетов в столбце для нечетных катетов.

- в первых четырех столбцах наблюдается резкий рост линейных размеров треугольников ( по всем сторонам), но несколько выделяется вторая строка.

- в столбце разной четности катеты содержат исключительно множители 2,3,5, но и здесь не без оговорки выделяются одиннадцатая и пятнадцатая строки.

Строка 15 претендует на начальную строку нового блока троек чисел.

Множители столбца катетов разной четности соответствуют ключевым числам пирамид на плато Гизе и «единичных пирамид» тел Платон, т.е. имеется тот же ряд основополагающих цифр. – 1,2,3,4,5.

Конечно, желательно заново проанализировать все математические таблички Древнего Вавилона, поскольку фрагмент в виде глиняной таблички «Plimpton 322» представляется только частью некой математической системы знаний. Возможно, и перевод в современное исчисление требует некоторой корректировки, тогда и выводы могут быть более строгими.

6. Практическая часть «Записки программиста»

repeat

a:=a/2;

until a+1=1;

Для написания программы была использована среда программирования Borland Delphi 7 как наиболее простая и одновременно достаточно гибкая для поставленных задач. А именно:

• Придумать алгоритм, который строит пирамиду в пространстве (как особый вид, так и подобия реально существующих пирамид);

• Связать алгоритм с языком программирования и получить результат;

• Добавить пользовательский интерфейс (этой теме можно посвящать отдельный реферат, ибо тема проблемная).

• Собрать все вместе и разнообразить построение пирамидки анимацией.

Будет справедливо кратко сказать о каждой из задач по отдельности, привести расчеты и некоторые нюансы исполнения.

6.1 Алгоритм

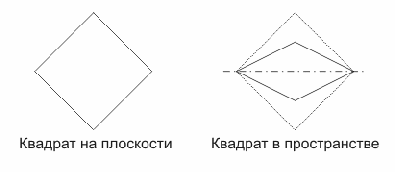
Над этим алгоритмом думали долго, рисовали, пробовали и в конце концов пришли к довольно простому и в то же время эффективному решению. Чтобы построить пирамиду в пространстве нужно построить основание, высоту и соединить точки. Так как в пространстве сохраняется только параллельность, из квадрата в основании должен получиться параллелограмм, а самый простой способ это сделать – сжать квадрат в 2 раза по вертикали вот таким образом:

Далее добавляется вершина – конец нормали, проведенной из центра квадрата в основании и добавляются некоторые дополнительные линии. И это было бы не сложно, если бы пирамидка не должна была крутиться вокруг вертикали. Что же делать теперь? Как осуществить перенос в пространстве? Мы попытались решить эту задачу - весь алгоритм построения пирамидки можно разделить на 3 этапа: просчет основания, пересчет основания в пространстве и доп. вычисления, рисование.

Просчет основания.

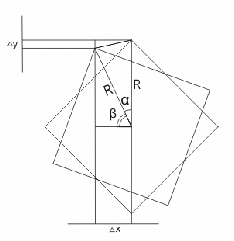
Это самая сложная часть, так как здесь нужно сделать поворот квадрата на некоторый угол в координатах. Для начала пусть квадрат повернут таким образом:

Тогда справедливы следующие равенства:

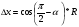
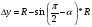
И при повороте каждая координата каждого угла меняется на 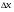или 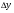. Теперь можно посчитать координаты углов квадрата при любом угле поворота.

Пересчет основания в пространстве.

Довольно простая операция, когда из каждой у-координаты вершины вычитается у-координата центра, делится на 2, а потом обратно прибавляется к у центра. Таким образом квадрат сжимается к оси, проходящей через центр квадрата и параллельной ох.

Также тут просчитываются координаты вершины пирамиды и середины квадрата

Рисование.

Когда все точки просчитаны, можно безбоязненно водить виртуальным карандашом по окошку программы. Здесь задается цвет карандаша и толщина линии.

6.2 Язык программирования

Теперь, когда алгоритм готов, можно приступить к собственно написанию кода. Код полностью я приведу позже с комментариями, а пока что общая структура. Программа состоит из нескольких функций, привязанных к событиям (например нажатие кнопки – событие, а построение – функция). Для просчета и хранения координат я использовал двумерный массив pix[] примерно такого содержания:

pix

[1,..]

[2,..]

[3,..]

[4,..]

[5,..]

[6,..]

[..,1]

x1

x2

х3

х4

х вершины

…

[..,2]

y1

y2

у3

у4

у вершины

…

Где х1..х4 и у1..у4 – координаты вершин основания. Все компоненты, использованные при написании программы взяты из стандартных библиотек.

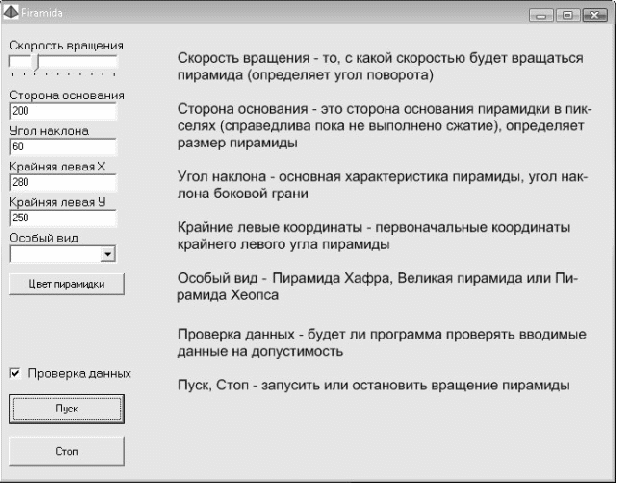
6.3 Интерфейс

Пользовательские интерфейсы – метод взаимодействия пользователя с программой для передачи ей инструкций и данных. Мой интерфейс состоит из четырех полей для ввода, трех кнопок, одного выкидного списка, одного ползунка и одной галочки (CheckBox). Размещен интерфейс слева так, что вводимые данные сверху, а кнопки снизу для удобства и чтобы пользователь мог сразу найти кнопку пуска.

6.4 Листинг

Строки, начинающиеся с // - комментарии, при компиляции опускаются и служат для напоминания программисту, что же он такое натворил вчера.

//Начало, подключение библиотек, объекты, глобальные переменные

unit Unit1;

interface

uses

SysUtils, Classes, Graphics, Forms, Dialogs, Windows,

Controls, StdCtrls, ComCtrls, ExtCtrls;

type

TForm1 = class(TForm)

Button1: TButton;

Edit1: TEdit;

Edit2: TEdit;

Edit3: TEdit;

Label1: TLabel;

Label3: TLabel;

Label4: TLabel;

Label2: TLabel;

Edit4: TEdit;

Timer1: TTimer;

Button2: TButton;

Speed: TTrackBar;

Label5: TLabel;

Test: TCheckBox;

ComboBox1: TComboBox;

Label6: TLabel;

ColorDialog1: TColorDialog;

ColorB: TButton;

Stats: TLabel;

Fill: TCheckBox;

RazmB: TButton;

Timer2: TTimer;

procedure Button1Click(Sender: TObject);

procedure Timer(Sender: TObject);

procedure Button2Click(Sender: TObject);

procedure FormCreate(Sender: TObject);

procedure SpeedChange(Sender: TObject);

procedure ComboBox1Change(Sender: TObject);

procedure ColorBClick(Sender: TObject);

procedure RazmBClick(Sender: TObject);

procedure Timer2Timer(Sender: TObject);

private

{ Private declarations }

error: boolean;

x,y : Longint;

pix : array[1..20,1..20] of Longint;

a,a_plus,tmp: Real;

old: TColor;

i,H1_x,H1_y,H2_x,H2_y,H3_x,H3_y,temp :integer;

public

{ Public declarations }

end;

var

Form1: TForm1;

implementation

{$R *.dfm}

procedure TForm1.Button1Click(Sender: TObject);

begin

// Кнопка пуска

// Идет долгая и упорная проверка введенных пользователем данных

try

if Test.State=cbChecked then begin

if (StrToFloat(Edit1.Text)*sqrt(2))>(ClientWidth-150) then begin

ShowMessage('При текущей ширине окна данная сторона основания слишком велика');

error:=true; end;

if (StrToFloat(Edit4.Text)>=90) or (StrToFloat(Edit4.Text)<=0) then begin

ShowMessage('Угол наклона должен быть больше 0 и меньше 90 градусов');

error:=true; end;

if (StrToFloat(Edit2.Text)<(StrToFloat(Edit1.Text)*sqrt(2)/4)) or (StrToFloat(Edit2.Text)>ClientHeight-(StrToFloat(Edit1.Text)*sqrt(2)/4)) then begin

ShowMessage('Крайняя левая Х либо залезает на интерфейс, либо слишком велика для текущей стороны основания');

error:=true; end;

if (StrToFloat(Edit3.Text)<150) or (StrToFloat(Edit2.Text)>ClientWidth-(StrToFloat(Edit1.Text)*sqrt(2))) then begin

ShowMessage('Крайняя левая У либо слишком мала, либо слишком велика для текущей стороны основания');

error:=true; end;

end;

finally

if error=false then begin

Edit1.Enabled:=False;

Edit2.Enabled:=False;

Edit3.Enabled:=False;

Edit4.Enabled:=False;

Test.Enabled:=False;

Timer1.Enabled:=True; end;

error:=false;

end;

end;

procedure TForm1.Timer(Sender: TObject);

var

i,j,min:integer;

pol: array[1..3] of TPoint; // координаты точек треугольника

begin

// Главный таймер, по нему строится пирамида

// Расчет начальных значений

pix[1,1]:= StrToInt(Edit2.Text);

pix[1,2]:= StrToInt(Edit3.Text);

pix[2,1]:= Round( pix[1,1] + (StrToFloat(Edit1.Text)*sqrt(2))/2 );

pix[2,2]:= Round( pix[1,2] - (StrToFloat(Edit1.Text)*sqrt(2))/2 );

pix[3,1]:= Round( pix[1,1] + StrToFloat(Edit1.Text)*sqrt(2) );

pix[3,2]:= pix[1,2];

pix[4,1]:= Round( pix[1,1] + (StrToFloat(Edit1.Text)*sqrt(2))/2 );

pix[4,2]:= Round( pix[1,2] + (StrToFloat(Edit1.Text)*sqrt(2))/2 );

pix[5,1]:= pix[2,1];

tmp:= sin(StrToFloat(Edit4.Text)*Pi/180)/cos(StrToFloat(Edit4.Text)*Pi/180)*StrToFloat(Edit1.Text)/2;

pix[5,2]:= Round( pix[1,2] - tmp );

// Поворот на a радиан

x:= Round( (StrToFloat(Edit1.Text)*sqrt(2))/2 - sin(PI/2-a)*(StrToFloat(Edit1.Text)*sqrt(2))/2 );

y:= Round( cos(PI/2-a)*(StrToFloat(Edit1.Text)*sqrt(2))/2 );

pix[1,1]:= pix[1,1] + x;

pix[1,2]:= pix[1,2] + y;

pix[2,1]:= pix[2,1] - y;

pix[2,2]:= pix[2,2] + x;

pix[3,1]:= pix[3,1] - x;

pix[3,2]:= pix[3,2] - y;

pix[4,1]:= pix[4,1] + y;

pix[4,2]:= pix[4,2] - x;

// Уменьшаем основание вдвое по оси у

pix[1,2]:= Round( pix[1,2] - y/2 );

pix[2,2]:= Round( pix[2,2] + ((StrToFloat(Edit1.Text)*sqrt(2)/2 - x)/2) );

pix[3,2]:= Round( pix[3,2] + y/2 );

pix[4,2]:= Round( pix[4,2] - ((StrToFloat(Edit1.Text)*sqrt(2)/2 - x)/2) );

with Canvas do begin

Brush.Color:= old;

FillRect(Rect(150,0,ClientWidth,ClientHeight));

// Основные линии

Pen.Width:= 2;

Pen.Color:= ColorDialog1.Color;

MoveTo(pix[1,1],pix[1,2]);

for i:=4 downto 1 do

LineTo(pix[i,1],pix[i,2]);

MoveTo(pix[1,1],pix[1,2]);

LineTo(pix[5,1],pix[5,2]);

LineTo(pix[3,1],pix[3,2]);

MoveTo(pix[2,1],pix[2,2]);

LineTo(pix[5,1],pix[5,2]);

LineTo(pix[4,1],pix[4,2]);

// Вспомогательные линии

Pen.Width:=1;

MoveTo(pix[1,1],pix[1,2]); LineTo(pix[3,1],pix[3,2]);

MoveTo(pix[2,1],pix[2,2]); LineTo(pix[4,1],pix[4,2]);

MoveTo(pix[5,1],pix[5,2]); LineTo(pix[5,1],pix[5,2]+Round(tmp));

end;

end;

a:=a+a_plus;

end;

procedure TForm1.Button2Click(Sender: TObject);

begin

// Кнопка остановки

Timer1.Enabled:=False;

Timer2.Enabled:=False;

Edit1.Enabled:=True;

Edit2.Enabled:=True;

Edit3.Enabled:=True;

Edit4.Enabled:=True;

Test.Enabled:=True;

end;

procedure TForm1.FormCreate(Sender: TObject);

begin

//Создание формы, начальные значения переменных

old:=Canvas.Brush.Color;

a:=0;

a_plus:=0.05;

end;

procedure TForm1.SpeedChange(Sender: TObject);

begin

// Изменение скорости, ползунок

a_plus:=Speed.Position/30;

end;

procedure TForm1.ComboBox1Change(Sender: TObject);

begin

// Выбор вида пирамидки из списка

if ComboBox1.ItemIndex=0 then Edit4.Text:='43,3138';

if ComboBox1.ItemIndex=1 then Edit4.Text:='41,9699';

if ComboBox1.ItemIndex=2 then Edit4.Text:='40,8933';

end;

procedure TForm1.ColorBClick(Sender: TObject);

begin

// По кнопке включается выбор цвета

ColorDialog1.Execute

end;

end.

Заключение.

Итак, нами была создана научная программа, которая, безусловно, может быть применима как пособие на уроках геометрии в курсе изучения объемных тел, а в частности – пирамид; исследована часть исторического материала по теме «Великие пирамиды».

Бесспорно, такое направление знаний многогранно и объемно. Происходит слияние алгебры и геометрии. Тригонометрия становится частным направлением пирамидометрии, поскольку осуществимы действия с углами без перевода их в градусную меру.

В рассмотренной нами литературе говорится о том, что такой качественный скачек в освоении математики позволит преобразить точные науки и усилить прикладные дисциплины.

Великие пирамиды древности несут в себе большой вклад в историю развития как интеллектуальные послания из глубин тысячелетий, так и сокровищницы системы красивейших математических законов.

Список литературы.

1. Ван дер Варден Б.Л. «Пробуждающая наука математика Древнего Египта, Вавилона и Греции» - 1990. - №5

2. Даан- Дальмедико А., Пейфер Ж. «пути и лабиринты. Очерки по истории математики» - Л., 1990

3. Петросян П. «Вселенский шифр пирамид»// «Наука и религия»- 1992.- №12

4. Прохоров Ю.В. «Математический энциклопедический словарь»-М.: Советская энциклопедия, 1988.

5. Уваров В.В. «Пирамидометрия :Древнейшее математическое наследие» Л.: Издательство Уральского университета, 2000.

6. Фленов М. Е. Ф69 Библия Delphi. — СПб.: БХВ-Петербург, 2004. — 880 с.: ил.