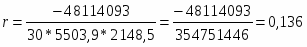
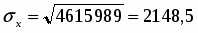
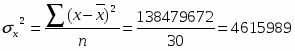
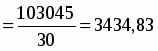
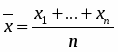
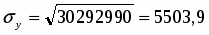
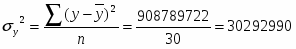
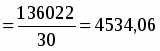
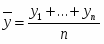
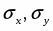
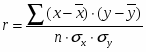
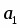
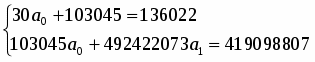
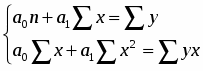
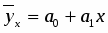
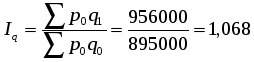
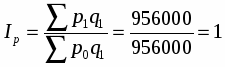
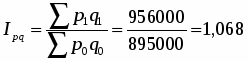
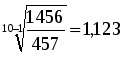
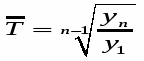
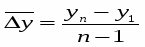
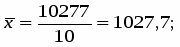
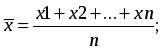
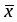
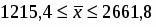
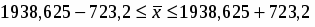
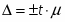
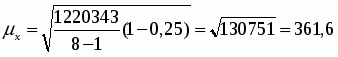
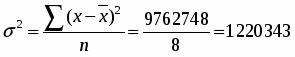
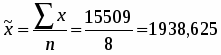
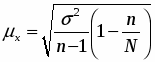
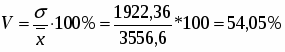
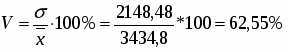
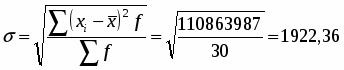
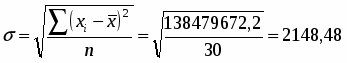
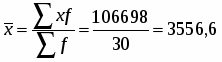
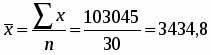
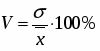
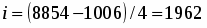
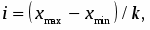
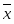
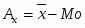
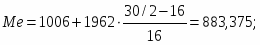
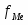
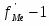
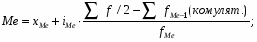
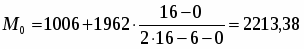
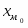
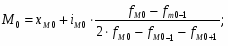
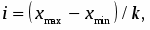1. Статистическая сводка. Группировка данных

Задание 1. Для целей анализа и сравнения применить характеристики центра группирования, к которым относятся средняя арифметическая, мода и медиана. Для характеристики степени отклонения распределения частот от симметричной формы рассчитать показатели эксцесса и ассиметрии. Проанализировать полученные значения показателей центра распределения и формы распределения. Сформулировать вывод.

Решение:

Величина равного интервала рассчитывается по формуле:

где k – число выделенных интервалов.

Определим длину интервала для денежных средств: d=(8854-1006)/5=1569.6(т.р.)

Мода – часто встречающаяся характеристика признака. Для дискретного вариационного ряда – наибольшая частота. Для интервального вариационного ряда мода рассчитывается по следующей формуле:

- нижняя граница модального интервала

i– длина модального интервала

f_Mo – частота модального интервала

f_Mo+1 – частота интервала следующего за модальным

Модальный интервал – интервал с наибольшей частотой

х_Мо=1006; i_Mo =1962; f_Mo =16; f_Mo-1 =0; f_Mo+1 =6;

(т.р.)

Медиана – значение признака, делящее всю совокупность на две равные части. Интервальный вариационный ряд:

х_Ме – нижняя граница медианного интервала;

i – длина медианного интервала

- накопленная частота интервала предшествующая медианному.

- частота медианного интервала

Медианный интервал – первый интервал накопленная частота которого превышает половину от общей суммы частот.

х_Ме=1006; i_Mе =1962; f_Mе =16; f_Mе-1 =16, f=30.

Выявление общего характера распределения предполагает вычисление таких показателей распределение, как, асимметрия и эксцесс. Для симметричных распределений частоты двух вариант, равноотстоящих в обе стороны от центра распределения (вершины распределения), равны между собой. Для симметричных распределений совпадают между собой средняя, мода, медиана. Статистическим показателем, характеризующим асимметрию распределения, является относительный показатель асимметрии. Он рассчитывается по формуле:

=3556,6-2213,38=1343,22

— среднее значение признака;

M_o – мода;

A_s - относительный показатель асимметрии.

Если A_s положителен, то распределение имеет правостороннюю асимметрию, и общая частота признаков справа от вершины больше общей частоты признака слева от вершины.

Соотношение моды, медианы и средней арифметической указывает на характер распределения и позволяет оценить его асимметрию. Так в симметричных распределениях все эти три характеристики равны между собой. Чем больше расхождение между модой и средней арифметической , тем более асимметричен ряд. Для умеренно асимметричных рядов разность между модой и средней арифметической примерно в три раза превышает разность между медианой и средней.

Эксцесс (Э) - показатель, характеризующий остроту вершины распределения. Если Э положительный, то распределение называется островершинным. Это означает, что частота появления наибольшего значения признака существенно больше частот появления всех других значений признака.

Если Э отрицателен, то это означает, что частота появления наибольшего значение признака в выбранной статистической совокупности не очень велика по сравнению с частотами появления всех других значений признаков.

Наиболее интересный случай, когда Э принимает нулевое значение. В этом случае говорят, что статистическая совокупность (признак) имеет нормальное распределение.

Задание 2. Для выявления зависимости между экономическими показателями деятельности предприятий провести аналитическую группировку показателей 30 предприятий. Группировку провести с равными интервалами, выделив четыре или пять групп. Рассчитать коэффициенты вариации по группировочному признаку на основании исходных данных и по аналитической группировке согласно своего варианта. Объяснить расхождения в значениях полученных коэффициентов.

Решение:

Распределим предприятия по группировочному признаку денежные средства.

Величина равного интервала рассчитывается по формуле:

где k – число выделенных интервалов.

Определим длину интервала для денежных средств, число групп зададим равное 4:

(т.р.)

Коэффициент вариации рассчитаем по формуле:

Для расчета средних величин используем формулы средней арифметической простой и взвешенной в зависимости от исходных данных.

Среднее квадратическое отклонение так же рассчитаем по формуле простой (при расчете по исходным данным) и взвешенной.

Рассчитаем коэффициенты для исходных данных и по аналитической таблице:

_{Среднее квадратическое отклонение:}

Рассчитаем коэффициент вариации:

Вывод: в обоих расчетах коэффициент вариации значительно больше 33%. Следовательно, рассмотренная совокупность неоднородна и средняя для нее недостаточно типична.

2. Абсолютные и относительные показатели

Задание 1. Выполнить анализ показателей бухгалтерского баланса (Форма 1) или отчета о прибылях и убытках (Форма 2) путем расчета статистических показателей структуры и динамики. По результатам расчетов охарактеризовать основные тенденции изменения структуры в динамике.

Для выполнения аналитических исследований и оценок структуры актива и пассива баланса произвести группировку его статей.

Решение:

Проанализируем отчет о прибылях и убытках одного АО, в тыс. руб.:

Вывод: выручка от реализации увеличилась по предприятию на 1342 тыс. руб. или на 23,51%. Полная себестоимость реализованной продукции увеличилась на 1459 тыс. руб или на 29,71%, а прибыль от продаж уменьшилась на 117 тыс. рублей или на 14,66%. В итоге чистая прибыль уменьшилась на 86, 868 тыс. руб или на 11,93%.

В предыдущем году себестоимость проданных товаров составляла 83,78% от выручки, а в отчетном 88,27%, что повлияло на уровень прибыли от реализации.

В предыдущем году прибыль от реализации составляла 13,98% от выручки, а в отчетном всего 9,66%.

Показатели

Предыдущий год

Отчетный год

Удельный вес, %

Динамика

Предыдущий год

Отчетный год

абс. Измен, тыс. руб.

абс. Измен удельн веса, %

Темп роста, %

Темп прироста, %

Выручка от продажи продукции, работ, услуг (за минусом НДС и акцизов)

5708

7050

100,00

100,0

1342

0,00

123,51

23,51

Себестоимость проданных товаров, продукции, работ, услуг

4782

6223

83,78

88,27

1441

4,49

130,13

30,13

Коммерческие расходы

128

146

2,24

2,07

18

-0,17

114,06

14,06

Полная себестоимость реализованной продукции

4910

6369

86,02

90,34

1459

4,32

129,71

29,71

Прибыль (убыток) от продаж

798

681

13,98

9,66

-117

-4,32

85,34

-14,66

Прибыль от прочей реализации

145,9

160,7

2,56

2,28

14,8

-0,28

110,14

10,14

Внереализационные доходы

15,7

2,8

0,28

0,04

-12,9

-0,24

17,83

-82,17

Внереализационные расходы

1,6

0,8

0,03

0,01

-0,8

-0,02

50,00

-50,00

Прибыль (убыток) до налогообложения

958

843,7

16,78

11,97

-114,3

-4,82

88,07

-11,93

Текущий налог на прибыль (24%)

229,92

202,4

4,03

2,87

-27,432

-1,16

88,07

-11,93

Чистая прибыль (убыток)

728,08

641,2

12,76

9,10

-86,868

-3,66

88,07

-11,93

3. Выборочный метод в статистических исследованиях

Задание 1. Провести 25% механическую выборку из генеральной совокупности, представленной в табл. 2 по показателю, который является для вашего варианта результативным. С вероятностью 0,954 рассчитать границы изменения средней величины в генеральной совокупности (по табл. 2) и сравнить с результатом, полученным на основании расчета по выборочной совокупности. Начало отбора начинать с номера предприятия, совпадающего с номером вашего варианта. Сформулировать вывод.

Решение

№

Чистая прибыль отчетного периода, т.р.

(х-х ср)2

9

1523

172744

13

941

995256

17

2271

110473

21

2189

62687,6

25

1235

495088

29

4589

7024488

33

1754

34086,4

37

1007

867925

Итого

15509

9762748

Предельная ошибка выборки:

=2*361,6=723,2

Т.к. Р=0,954, то коэффициент доверия t=2

Среднее количество чистой прибыли находится в интервале:

Вывод: доверительные пределы для при уровне суждения 0,954 составляют от 1215,4 до2661,8 тыс. рублей.

4. Ряды динамики

Задание 1. По данным своего варианта исчислите:

1. Базисные, цепные и среднегодовые показатели абсолютного прироста, темпов роста и темпов прироста объемов индивидуального жилищного строительства.

2. Среднегодовой объем индивидуального жилищного строительства.

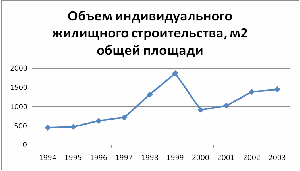
3. Изобразите динамику индивидуального жилищного строительства на графике.

Данные об объеме индивидуального жилищного строительства по району.

Период в годах

Год

Объем индивидуального жилищного строительства, м² общей площади

1994-2003

1994

457

1995

480

1996

632

1997

718

1998

1319

1999

1875

2000

919

2001

1032

2002

1389

2003

1456

Решение

Год

Объем индивидуального жилищного строительства, м² общей площади

Абсолютный прирост

Коэффициент роста

Темп роста

Темп прироста

абсолютное значение 1% прироста

Цепн.

Баз.

Цепн.

Баз.

Цепн.

Баз.

Цепн

Баз.

Цепн.

1994

457

1995

480

23

23

1,05

1,05

105,03

105,03

5,03

5,03

4,57

1996

632

152

175

1,32

1,38

131,67

138,29

31,67

38,29

4,80

1997

718

86

261

1,14

1,57

113,61

157,11

13,61

57,11

6,32

1998

1319

601

862

1,84

2,89

183,70

288,62

83,70

188,62

7,18

1999

1875

556

1418

1,42

4,10

142,15

410,28

42,15

310,28

13,19

2000

919

-956

462

0,49

2,01

49,01

201,09

-50,99

101,09

18,75

2001

1032

113

575

1,12

2,26

112,30

225,82

12,30

125,82

9,19

2002

1389

357

932

1,35

3,04

134,59

303,94

34,59

203,94

10,32

2003

1456

67

999

1,05

3,19

104,82

318,60

4,82

218,60

13,89

Итого

10277

Среднее значение объемов индивидуального жилищного строительства рассчитаем по средней простой

Ср. абсолютный прирост:

=(1456-457)/(10-1)=111

Ср. темп роста.

==112,3%

Ср. темп прироста.

%=112,3%-100%=12,3%

5. Индексный метод

Задание 1. По данным своего варианта определите:

1. Общие индексы:

а) цен,

б) физического объема проданных товаров;

в) товарооборота.

Какую роль в изменении товарооборота сыграли изменения цен и количества проданных товаров?

2. Абсолютную величину изменения расходов населения в связи с изменением цен.

Реализация товаров в магазине.

Вид товара

Предыдущий год

Отчетный год

Количество, шт.

Цена за единицу, руб.

Количество, шт.

Цена за единицу, руб.

Линолеум полукоммерческий

1900

280

2000

280

Линолеум бытовой

1650

220

1800

220

Решение

Товар

Предыдущий год

Отчетный год

Количество, шт.

Цена за единицу, руб.

Количество, шт.

Цена за единицу, руб.

q0

p0

q1

p1

p0q0

p1q1

p0q1

Линолеум полукоммерческий

1900

280

2000

280

532000

560000

560000

Линолеум бытовой

1650

220

1800

220

363000

396000

396000

Итого:

3550

500

3800

500

895000

956000

956000

а) общий индекс товарооборота реализованной продукции:

б) общий индекс цены продукции:

Цены не повлияли на изменение товарооборота.

в) общий индекс физического объёма:

Увеличение физического объема на 6,8% повлияло на увеличение товарооборота на 6,8%.

Взаимосвязь индексов:

I_рq = I_р х I_q =1*1,068 = 1,068

Перерасход (экономия) покупателей от изменения товарооборота:

_pq = p₁q₁ - p₀q₀ = 956000 – 895000 = 61000 (руб.)

в том числе за счет роста цен:

_pq (p) = p₁q₁ - p₀q₁=956000 - 956000=0 ( руб.);

за счет динамики физического объема:

_pq (q) = p₀q₁ - p₀q₀ =956000 - 895000 =61000 (руб.).

Проверка: 61000 = 0 +61000

Выводы: Товарооборот реализованной продукции на рынке повысился на 6,8 %, физическая масса проданных товаров в отчетном периоде по сравнению с базисным увеличилась на 6,8 %, уровень цен не изменился. Расходы покупателей не изменились, т.к. цены в отчетном периоде остались не именными по отношению к базисному.

6. Статистическое изучение взаимосвязей

Задание 1. Для выявления зависимости между группировочным и результативным показателями рассчитайте линейный коэффициент корреляции по исходным данным своего варианта.

№

Чистая прибыль отчетного периода, т.р.

Денежные средства, т.р.

№

Чистая прибыль отчетного периода, т.р.

Денежные средства, т.р.

№

Чистая прибыль отчетного периода, т.р.

Денежные средства, т.р.

9

1523

1378

19

6154

6222

29

4589

1202

10

24971

1901

20

1170

8854

30

1579

7555

11

8124

6082

21

2189

1537

31

1570

4393

12

1478

1638

22

1776

3136

32

1321

4400

13

941

4999

23

1621

1006

33

1754

3650

14

18180

1576

24

9882

2232

34

3501

5718

15

3030

2387

25

1235

2810

35

2160

3417

16

13123

6031

26

8882

1277

36

2363

2942

17

2271

1299

27

4813

1085

37

1007

1972

18

2017

3757

28

1653

6701

38

1145

1888

Итого

136022

103045

Решение:

Предположим наличие линейной зависимости между рассматриваемыми признаками. Уравнение связи будет иметь следующий вид:

Денежные средства, т.р., х

Чистая прибыль отчетного периода

x2

xy

Yx

(x-xср)2

(Y-Yср.)2

(x-x_ср) *

*(у-у_ср.)

1378

1523

1898884,0

2098694,0

5248,7

4230563,4

9066522

6193262

1901

24971

3613801,0

47469871,0

5067,0

2352644,7

417668244

-31346850

6082

8124

36990724,0

49410168,0

3614,3

7007491,4

12887621

9503152

1638

1478

2683044,0

2420964,0

5158,4

3228610,0

9339543

5491242

4999

941

24990001,0

4704059,0

3990,6

2446617,4

12910128

-5620155

1576

18180

2483776,0

28651680,0

5179,9

3455261,4

186211497

-25365516

2387

3030

5697769,0

7232610,0

4898,1

1097954,7

2262217

1576011

6031

13123

36372961,0

79144813,0

3632,0

6740081,4

73769776

22298302

1299

2271

1687401,0

2950029,0

5276,2

4561784,0

5121471

4833533

3757

2017

14115049,0

7577869,0

4422,1

103791,4

6335625

-810915

6222

6154

38713284,0

38290188,0

3565,7

7768298,0

2624184

4515024

8854

1170

78393316,0

10359180,0

2651,2

29367367,4

11316945

-18230438

1537

2189

2362369,0

3364493,0

5193,5

3601771,4

5499338

4450546

3136

1776

9834496,0

5569536,0

4637,9

89301,4

7606932

824202

1006

1621

1012036,0

1630726,0

5378,0

5899231,4

8485957

7075353

2232

9882

4981824,0

22056624,0

4952,0

1446808,0

28600391

-6432672

2810

1235

7896100,0

3470350,0

4751,2

390416,7

10883841

2061367

1277

8882

1630729,0

11342314,0

5283,8

4656244,7

18904524

-9382115

1085

4813

1177225,0

5222105,0

5350,5

5521716,7

77804

-655447

6701

1653

44903401,0

11076753,0

3399,3

10667844,7

8300545

-9410044

1202

4589

1444804,0

5515978,0

5309,9

4985544,7

3018

-122657

7555

1579

57078025,0

11929345,0

3102,5

16975773,4

8732419

-12175367

4393

1570

19298449,0

6897010,0

4201,2

918083,4

8785691

-2840070

4400

1321

19360000,0

5812400,0

4198,7

931546,7

10323797

-3101145

3650

1754

13322500,0

6402100,0

4459,3

46296,7

7728771

-598178

5718

3501

32695524,0

20018718,0

3740,8

5212850,0

1067227

-2358663

3417

2160

11675889,0

7380720,0

4540,3

318,0

5636193

42338

2942

2363

8655364,0

6951946,0

4705,3

242884,7

4713530

1069974

1972

1007

3888784,0

1985804,0

5042,3

2139881,4

12440199

5159511

1888

1145

3564544,0

2161760,0

5071,5

2392693,4

11485773

5242321

103045

136022

492422073

419098807

136022

138479672,2

908789722

-48114093

n – число наблюдений; отсюда: а₀= 5727,48; а₁= -0,3474, т.к. <0 оценим связь как обратную.

Следовательно, уравнение корреляционной связи: y_x=81,178х-37445,94

Рассчитаем линейный коэффициент корреляции по формуле:

где - среднее квадратическое отклонение факторного и результативного признаков.

Таким образом, линейный коэффициент корреляции будет равен:

Вывод: Значение линейного коэффициента корреляции говорит о наличии слабой связи по шкале Чеддока и о том, что 13,6% изменений результата происходит под влиянием фактора.

Список литературы

1. Белявский И.К. и др. Статистика рынка товаров и услуг: Учебник. -М: Финансы и статистика, 1995.

2. Елисеева И.И, Юзбашев М.М. Общая теория статистики: Учебник. -М.: Финансы и статистика,1995.

3. Методические указания и решение типовых задач по статистике социально-экономической и отраслевой / Под ред. Т.Г. Храмцовой. - Новосибирск, 1990.

4. Ряузов Н.Н. Общая теория статистики: Учебник. -М.: Финансы и статистика, 1984.

5. Статистика: Учебно – методическое пособие/ Под ред. Т.Г. Храмцовой. - Новосибирск, 1999.