Конспект урока на тему «Решение простейших тригонометрических неравенств»
Учебная дисциплина:Математика.
Тема: «Решение простейших тригонометрических неравенств»
Тип урока:урок усвоения нового материала с элементами первичного закрепления.
Цели урока:
1) образовательные:
показать алгоритм решения тригонометрических неравенств с использованием единичной окружности.
учить решать простейшие тригонометрические неравенства.
2) развивающие:
развитие умения обобщать полученные знания;
развитие логического мышления;
развитие внимания;
развитие у учащихся грамотной устной и письменной математической речи.
3) воспитательные:
учить высказывать свои идеи и мнения;
формировать умения помогать товарищам и поддерживать их;
формировать умения определять, чем взгляды товарищей отличаются от собственных.
Методическая цель: показать технологию овладения знаниями на уроке изучения новых знаний.
Методы обучения:
наглядно - иллюстративный;
Дидактическая цель урока: Создание условий:
для соединения новой информации с уже изученным материалом;
для развития умения осуществлять анализ и отбор необходимой информации;
для развития умений делиться своими идеями и мнениями.
для развития логики, навыков рефлексии.
Форма организации учебной деятельности: коллективная, индивидуальная.
Оборудование:
учебник Колмогорова А. Н. «Алгебра и начала анализа», 10-11 класс;
проектор, доска;
презентация MS PowerPoint.
План урока:
Организационный момент(1 мин);
Проверка домашнего задания(7 мин);
Изучение нового материала (31 мин);
Домашнее задание(3 мин);
Подведение итогов (3 мин)
Тема урока:Решение простейших тригонометрических неравенств.
Выполнила: преподаватель математики КГБОУ НПО «ПУ №44» Мозер О. С.
Этапы деятельности
Деятельность преподавателя
Деятельность обучающихся
Примечание
I.Организационный момент.
Взаимные приветствия преподавателя и учащихся, фиксация отсутствующих; проверка внешнего состояния кабинета; проверка готовности учащихся к уроку; организация внимания.
Преподаватель:
- Здравствуйте! Мы на прошлых уроках учились решать простейшие тригонометрические уравнения, а сегодня будем учиться решать простейшие тригонометрические неравенства. Открываем тетради, записывает число и тему урока: «Решение простейших тригонометрических неравенств»
1.Обучающиеся приветствуют преподавателя.
2. Открывают тетради и записывают число.
Презентация. Слайд №1
II. Проверка домашнего задания.
Преподаватель:
- Для начала проверим домашнее задание.
Преподаватель вызывает по журналу двоих учащихся к доске.
Двое учащихся выходят к доске записывают упражнения и объясняют решение. Первый учащийся записывает упражнения под буквой а) б), а второй – в) г) д).
а)
 б)
б)
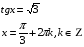
в)
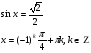
г)
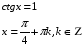
д)
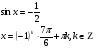
II. Актуализация
Преподаватель проводит фронтальный опрос:
- Теперь вспомним понятия изученные ранее:
1. Дайте определение единичной окружности.
2. Дайте определение линии синуса;
3. Дайте определение линии косинуса;
4. Дайте определение линии тангенса;
5. Дайте определение линии котангенса;
Примерные ответы учащихся:
1) Единичной окружностью называется окружность с радиусом единица.
2) Отрезок [-1; 1]оси ординат- называют линией синуса;
3) Ось абсцисс называют линией косинуса;
4) Касательную к единичной окружности в точке (1;0) называют линией тангенса;
5) Касательную к единичной окружности в точке (1;0) называют линией тангенса;
III. Новый материал
Преподаватель:
- На прошлом уроке мы решали простейшие тригонометрические уравнения, сегодня узнаем, как с помощью единичной окружности решить простейшее тригонометрическое неравенство. Решение неравенств, содержащих тригонометрические функции, сводится, как правило, к решению простейших тригонометрических неравенств вида sin x ≤ a, cos x >a, tg x ≥a, ctg x <a и т.д.
Решение тригонометрических неравенств рассмотрим на конкретных примерах с помощью единичной окружности:
sin x ≤
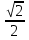
Алгоритм решение данного неравенства:
Для начала определим
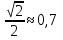
На Оу отмечаем значение и соответствующие точки на окружности;
Выделяем нижнюю часть окружности (обход совершаем против часовой стрелки).
Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение.
Записываем ответ:
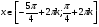
Аналогично по алгоритму, преподаватель и учащиеся решают следующие примеры:
Cos x ≥
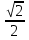 ;
;Sin x
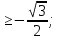
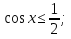
tg x≤
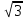 ;
;tg x
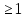 .
.
Учащиеся записывают алгоритм решения простейших тригонометрических неравенств в тетрадь.
Слайд №2
Слайд №3
Слайд №4
Слайд №5
Слайд№6
Слайд№7
IV. Домашнее задание
- Записываем домашнее задание§3, п. 10, стр. 77, упр. №154 -156 в) д).
Учащиеся записывают задание в тетрадь.
Слайд №8
V. Подведение итогов
Преподаватель подводит итог урока:
- Итак, сегодня на уроке мы познакомились с алгоритмом решения простейших тригонометрических неравенств.
-Урок закончен! До свиданья!
Обучающиеся рассказывают алгоритм решения простейших тригонометрических неравенств с помощью единичной окружности.

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ