Конспект урока с презентацией по теме"Треугольники" 9 класс
Урок обобщающего повторения
по геометрии в 9-м классе на тему: "Треугольники"
Тип урока: урок обобщения и систематизации знаний.
Цель урока:
повторить и обобщить тему “Треугольники”;
отрабатывать умение применять теорему Пифагора, теорему косинусов, теорему синусов решая задачи, тесты;
развивать, выработать активность, внимание, логическое мышление, монологическую речь, интерес к предмету, коллективное обучение;
ХОД УРОКА
1. Организация начала урока.
Треугольник… Знакомый вам с детства, и начиная с 7 класса, с уроков геометрии, геометрическая фигура, таит в себе немало интересного и загадочного, как Бермудский треугольник, в котором бесследно исчезают корабли и самолеты. Знакомые нам фигуры квадрат, параллелограмм, прямоугольник, ромб, трапеция состоят из двух треугольников, если провести одну диагональ и из четырех треугольников, если провести две диагонали. В 10-11 классах тоже применяются решения треугольников, поэтому вы должны научиться решать любой треугольник.
2. Проверка теоретических знаний.
Ответить на вопросы:
1. Какую фигуру называют треугольником?
2. Перечислите элементы треугольника.
3. Назовите виды треугольников по углам.
4. Назовите виды треугольников по сторонам.
5. Какой треугольник называется равносторонним?
6. Как называется третья сторона в равнобедренном треугольнике?
7. Перечислите свойства равнобедренного треугольника.
8. Перечислите свойства равностороннего треугольника.
9. Перечислите свойства прямоугольного треугольника.
10. Синусом, косинусом, тангенсом что называем?
11. Что такое неравенство треугольника?
12. Признаки равенства треугольников.
13. Подобие треугольников.
14. . В треугольнике KLN, KL=8,4 cм, LN=13,2 см, KN=7,5 см. Какой угол треугольника наибольший, какой наименьший?
15. Стороны треугольника 10см, 12см, 7см. Может ли угол, противолежащий стороне 7см, быть тупым? Почему?
16. Стороны треугольника 9см и 12см. Может ли угол, противолежащий стороне равной 9см, быть прямым? Почему?
17. Какие из следующих треугольников существуют? И почему?
5 см, 5 см, 5 см.
3 м, 6 м, 3 м.
12 дм, 3 дм, 8 дм.
3 см, 4 см, 5 см.
18. Как называется треугольник со сторонами 3, 4, 5?
3. Проверка домашнего задания.
Историческая справка. (сообщения учащихся)
Египетский треугольник
Материал из Википедии — свободной энциклопедии
Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.
Особенностью такого треугольника, известной ещё со времён античности, является то, что все три стороны его целочисленны, а по теореме Пифагора он прямоуголен. Египетский треугольник является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.
Название треугольнику с таким отношением сторон дали эллины: в VII—V веках до н. э. греческие философы и общественные деятели активно посещали Египет. Так, например, Пифагор в 535 до н. э. по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к доказательству знаменитой теоремы.
Общепринято мнение, что египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов египетскими землемерами и архитекторами, например, при построении пирамид. Однако некоторые историки науки, например, голландский математик Ван дер Варден, считают, что это только укоренившееся заблуждение, гипотеза немецкого математика Кантора, ставшая общепринятой из-за непроверяемости источников в ранних исследованиях по истории. В архитектуре средних веков египетский треугольник применялся для построения схем пропорциональности.
Для построения прямого угла использовался шнур или верёвка, разделённая отметками (узлами) на 12 (3+4+5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры-катеты являлись направляющими для кладки прямого угла сооружения.
Теорема Пифагора
В древнекитайской книге Чу-пей (англ.) (кит. 周髀算經) говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Мориц Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам ещё около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора, гарпедонапты, или «натягиватели верёвок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Очень легко можно воспроизвести их способ построения. Возьмём верёвку длиною в 12 м и привяжем к ней по цветной полоске на расстоянии 3 м от одного конца и 4 метра от другого. Прямой угол окажется заключённым между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становится излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, — например, рисунки, изображающие столярную мастерскую.
Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммурапи, то есть к 2000 году до н. э., приводится приближённое вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой — на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал вывод о большой вероятности того, что теорема о квадрате гипотенузы была известна в Индии уже около XVIII века до н. э.
Согласно комментарию Прокла к Евклиду, Пифагор (годами жизни которого принято считать 570—490 гг. до н. э.) использовал алгебраические методы, чтобы находить пифагоровы тройки. Однако Прокл писал между 410 и 485 гг. н. э. Томас Литтл Хит (en:Thomas Little Heath) считал, что не существует явного упоминания, относящегося к периоду продолжительностью 5 веков после смерти Пифагора, что Пифагор был автором теоремы. Однако, когда авторы, такие как Плутарх и Цицерон, пишут о теореме Пифагора, они пишут так, как будто авторство Пифагора было широко известным и несомненным. «Принадлежит ли эта формула лично перу Пифагора…, но мы можем уверенно считать, что она принадлежит древнейшему периоду пифагорейской математики». По преданию, Пифагор отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков.
Приблизительно в 400 г. до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Приблизительно в 300 г. до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора.
Теорема синусов
Самое древнее доказательство для теоремы синусов на плоскости описано в книге Насир ад-Дин Ат-Туси «Трактат о полном четырёхстороннике» написанной в XIII веке. Теорема синусов для сферического треугольника была доказана математиками средневекового Востока ещё в X веке. В труде Ал-Джайяни XI века «Книга о неизвестных дугах сферы» приводилось общее доказательство теоремы синусов на сфере.
Теорема косинусов
Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» Евклида.
Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях математиков стран Средней Азии. Теорему косинусов для сферического треугольника в привычном нам виде сформулировал Региомонтан, назвав её «теоремой Альбатегния» (по имени ал-Баттани).
В Европе теорему косинусов популяризовал Франсуа Виет в XVI столетии. В начале XIX столетия её стали записывать в принятых по сей день алгебраических обозначениях.
4. Работа в группах
Группа А
А. Соотнесите высказывание с его названием или формулой.
Высказывание
Название, формулы
1. Треугольник называется равнобедренным, если две его стороны равны.
2. Если в треугольнике известны две стороны и угол между ними, то площадь треугольника можно вычислить по формуле …
3. Стороны треугольника пропорциональны синусам противолежащих углов.
4. Если в треугольник вписана окружность, то площадь треугольника вычисляется по формуле …
5. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
6. В равнобедренном треугольнике углы при основании равны.
7. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
8. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
9. Средняя линия треугольника параллельна стороне треугольника и равна ее половине.
10. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.
11. Внешний угол треугольника – это угол, смежный с углом треугольника.
а) определение равных треугольников;
б) признак равенства треугольников;
в) определение средней линии треугольника;
г) свойство средней линии треугольника;
д) определение равнобедренного треугольника;
е) свойство равнобедренного треугольника;
ж) теорема синусов;
з) теорема косинусов;
и) теорема Пифагора;
к) теорема Фалеса;
л) ![]() ;
;
м) ![]() ;
;
н) ![]() ;
;
о) ![]() ;
;
п) определение внешнего угла треугольника;
р) свойство внешнего угла треугольника;
с) определение подобных треугольников;
т) признак подобия треугольников.
Группа В
Найдите ошибки в тексте.
«Некий ученик написал сочинение по теме «Треугольники». Вот некоторые фрагменты его сочинения.
Треугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками.
Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести любую биссектрису, она будет являться медианой и высотой.
Площадь любого треугольника можно вычислить по формулам:
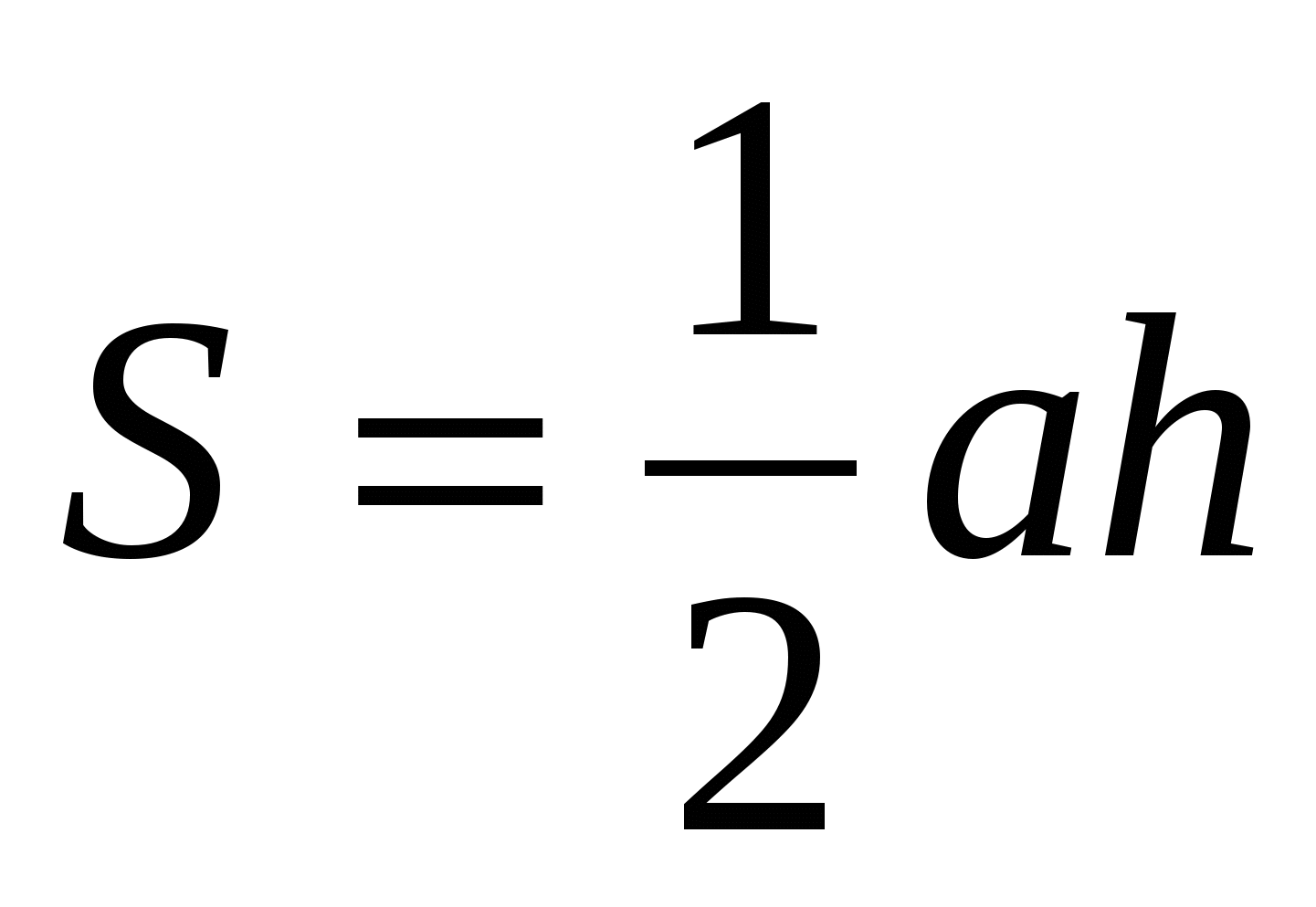 (*) и
(*) и 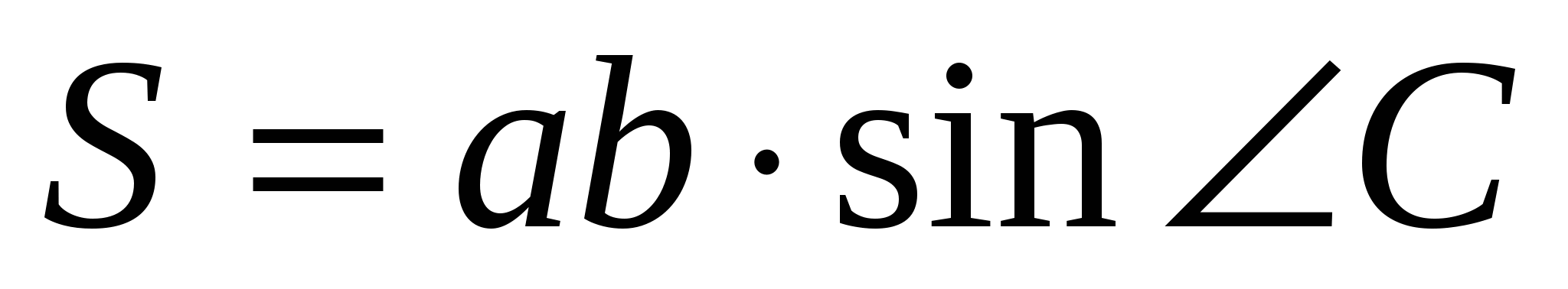 (**)
(**)Если в треугольник вписана окружность, то его площадь можно найти по формуле
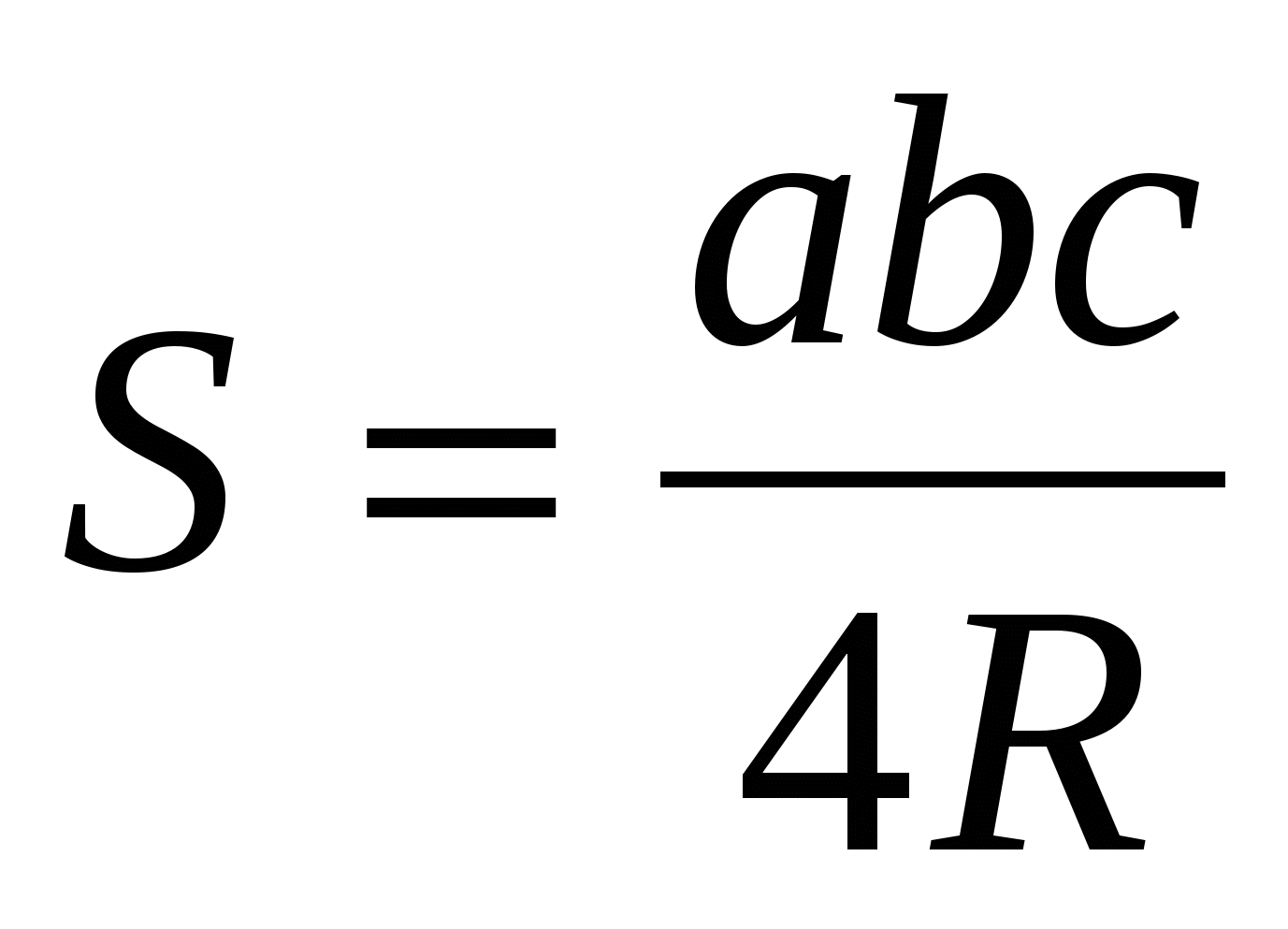 , где радиус этой окружности вычисляется по теореме косинусов:
, где радиус этой окружности вычисляется по теореме косинусов: 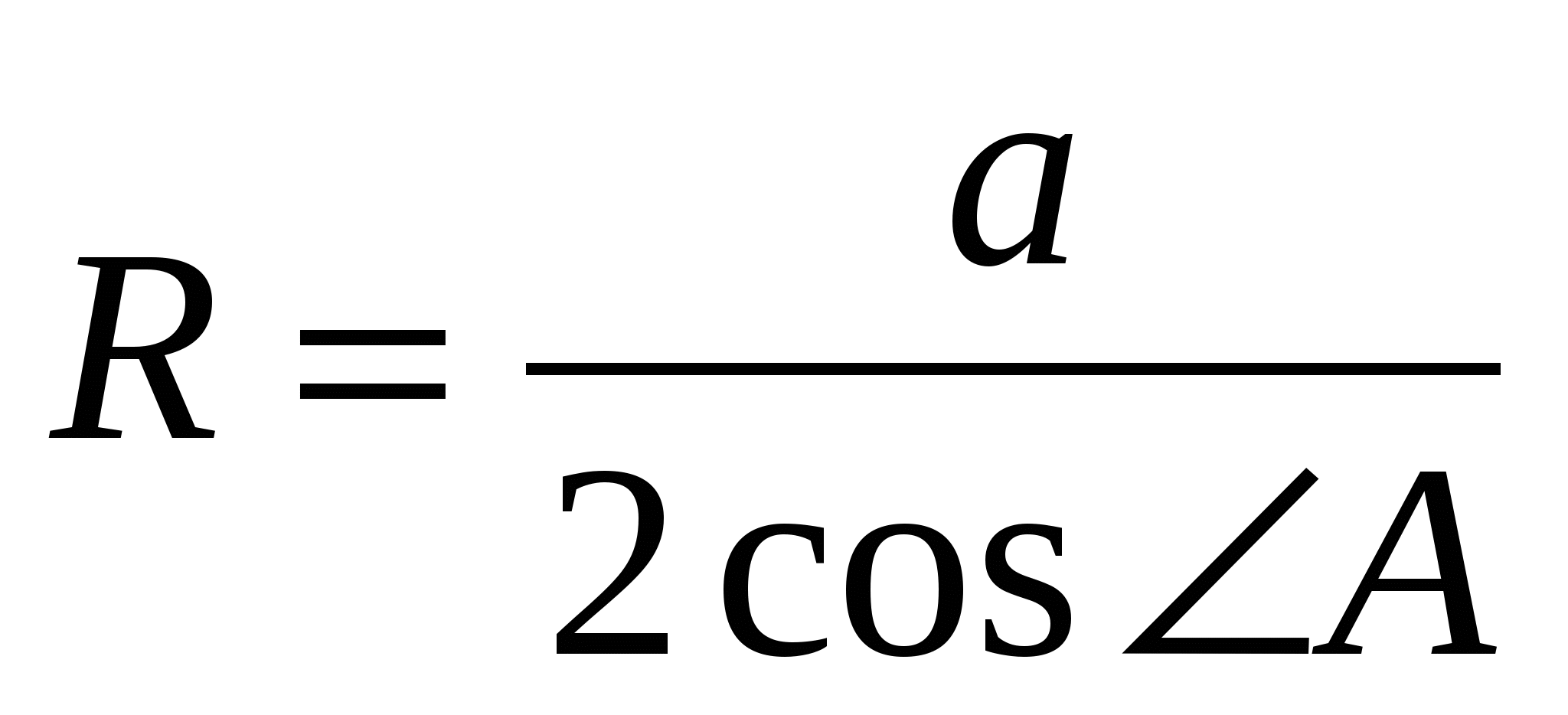 .
.А если около треугольника описать окружность, то для нахождения площади треугольника справедлива формула
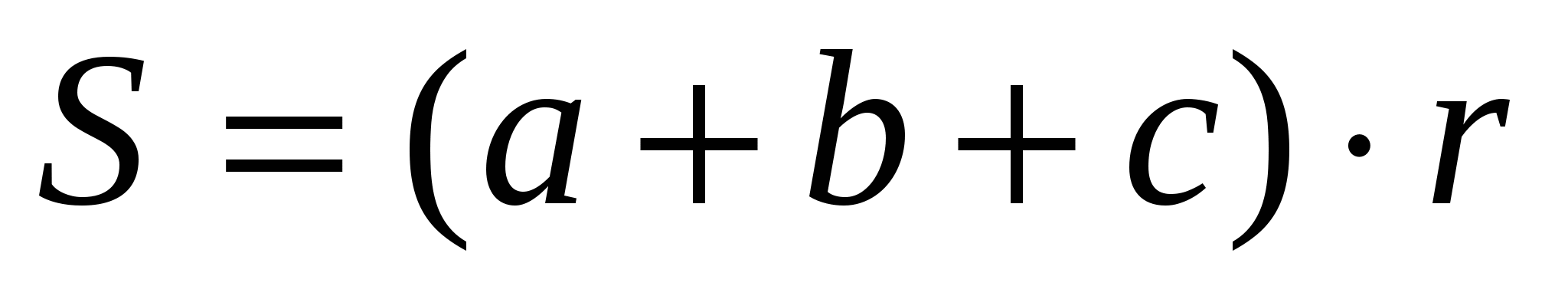 .
.Прямая, параллельная стороне треугольника, является его средней линией.
Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники равны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники подобны.
Все ли верно в сочинении ученика?»
5. Решение теста на применение теоремы Пифагора
1. Укажите, какой из рисунков содержит треугольники, к которым применима теорема Пифагора.

2. Сторона квадрата равна 3 см, тогда его диагональ равна:
а) 9 см; б) ![]() 6 см; в)
6 см; в) ![]() 3 см; г) 3
3 см; г) 3![]() 2 см.
2 см.
3. В равнобедренном треугольнике боковая сторона равна 10 см, а основание – 16 см, тогда высота опущенная на основание, равна:
а) 241 см; б) ![]() 6см; в)
6см; в) ![]() 26 см; г)
26 см; г) ![]() 6 см.
6 см.
4. Из одной точки на прямую опущены перпендикуляр и наклонная. Если перпендикуляр равен 9 см, а наклонная – 15 см, то длина проекции наклонной равна:
а) 12 см; б) 3![]() 34 см; в) 2
34 см; в) 2![]() 6 см; г)
6 см; г) ![]() 6 см.
6 см.
5. Из точки D к окружности с центром в точке о проведена касательная DF. Если OD=17 см, а FD=15 см, то радиус окружности равен:
а) ![]() 2 см; б) 8 см; в) 32 см; г) 4
2 см; б) 8 см; в) 32 см; г) 4![]() 2 см.
2 см.
6. Дан прямоугольный треугольник ABC. Гипотенуза AC=10 см, sinC=0,3. найдите катет AB.
Ответ: AB=3 см
7. В равнобедренном треугольнике одна сторона равна 11 см, а вторая – 4 см. найдите третью сторону.
Ответ: 4 см.
8. В прямоугольном треугольнике ABC:AC=17 см, BC=8 см, AB=15 см. найдите cosC.
Ответ: cosC=8/17.
9. В окружности с центром в точке О проведена хорда АВ, равная 18 см, если расстояние от центра окружности до хорды равно 12 см, то радиус окружности равен:
а) 15 см; б) ![]() 6 см; в) 6
6 см; в) 6![]() 13 см; г) 3
13 см; г) 3![]() 7 см.
7 см.
6. Разминка
Найдите лишнее слово:
сторона, медиана, катет, хорда, высота, гипотенуза;
вершина, биссектриса, диаметр, основание, периметр.
Сколько всего треугольников на рисунке?
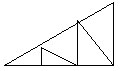
В равнобедренном треугольнике одна сторона равна 23, а другая 10. Какая из них является основанием треугольника?
7.Решение задач на применение теоремы синусов и теоремы косинусов
уровень А
Задача: Измерили дальномером расстояние СВ=62м, СА=80м. Угол между ними 600. Найдите расстояние между двумя деревьями А и В.
Решение:


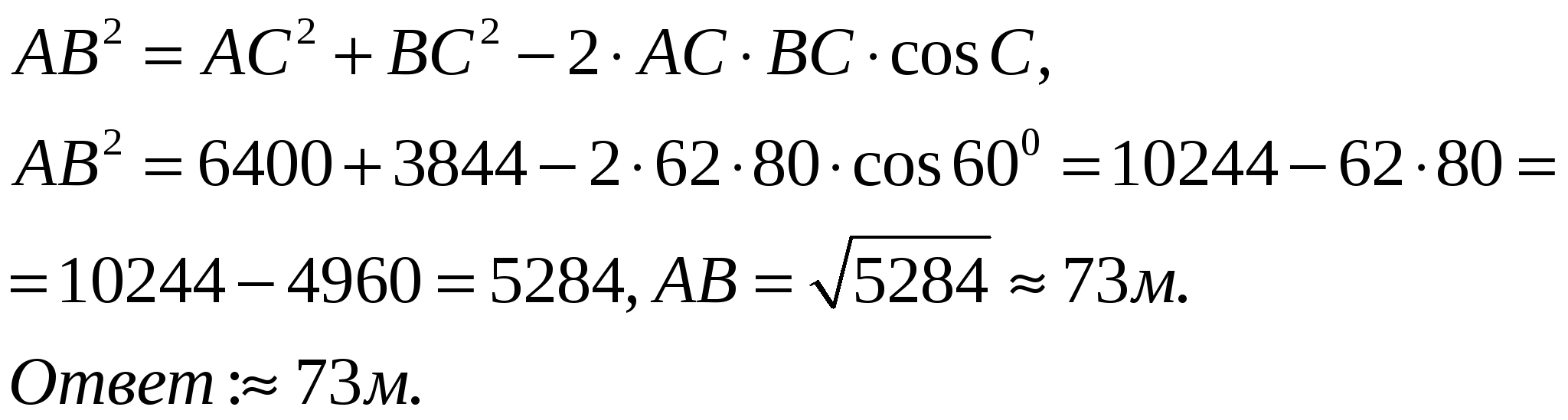
уровень В
Задача: Найти ширину озера АВ, если АС=120м, ![]() ,
,![]() .
.
Решение:



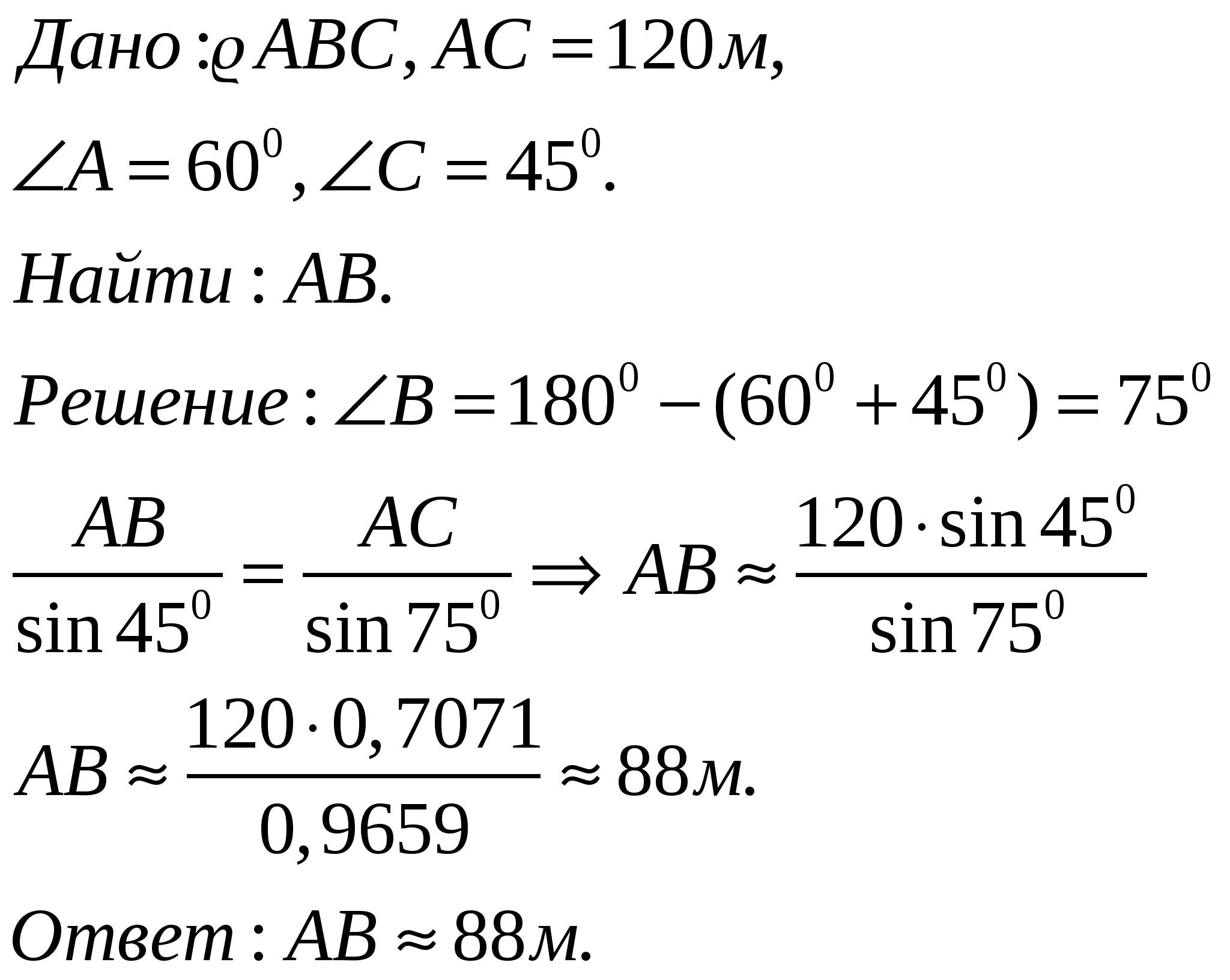
8. Подведение итогов урока
Ученики вместе с учителем обсуждают успехи и недостатки работы на уроке. Дают оценку деятельности учащихся и качества предложенных заданий
9. Домашнее задание
Уровень А
В треугольнике АВС АВ = 10, АС = 12. Периметр треугольника АВС равен 32.
1. Определите вид треугольника по длинам его сторон.
2. Найдите высоту, опущенную из вершины В.
3. Найдите площадь треугольника.
4. Найдите sinB.
5. Найдите радиус описанной около треугольника окружности.
6. Найдите радиус вписанной в треугольник окружности.
Уровень В
1.Две планки длиной 35см и 42см скреплены одним концом. Какой угол между ними надо взять, чтобы расстояние между другими концами планок равнялось 24см?
2. Верно ли, что в треугольник со сторонами, равными 5, 6, 7 можно вписать окружность с радиусом ![]() ?
?

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ