Нестеренко Олеся Викторовна

Учитель математики и информатики

МАОУ СОШ №45 г. Калининграда

Решение задач оптимизации в MS Excel

Задача 2.4. Решить симплексным методом задачу о составлении рациона питания животных, условия которой приведены в задаче 1.2.

Задача 1.2. Рацион для питания животных на ферме состоит из двух видов кормов I и II. Один килограмм корма I стоит 80 ден. ед. и содержит: 1 ед. жиров, 3 ед. белков, 1 ед. углеводов, 2 ед. нитратов. Один килограмм корма II стоит 10 ден. ед. и содержит 3 ед. жиров, 1 ед. белков, 8 ед. углеводов, 4 ед. нитратов.

Составить наиболее дешевый рацион питания, обеспечивающий жиров не менее 6 ед., белков не менее 9 ед., углеводов не менее 8 ед., нитратов не более 16 ед.

Решение:

Представим данные, содержащиеся в условии задачи, в табличном виде.

Питательное вещество

Число единиц питательных веществ на 1 кг корма

Необходимый минимум питательных веществ

I

II

Белки

3

1

9

Жиры

1

3

6

Углеводы

1

8

8

Нитраты

2

4

16 (max)

Цена 1 кг корма, р

80

10

Составим экономико-математическую модель задачи. Обозначим x₁, x₂ − количество кормов видов I и II, входящих в рацион питания. Тогда общая стоимость рациона (целевая функция) запишется в виде Z = 80 x₁ + 10 x₂ .

C учетом того, что количество единиц питательных веществ, входящих в

рацион кормления, не должно быть меньше (больше) указанного минимума

(максимума), ограничения запишутся в виде следующих неравенств:

3 x₁ +x ₂ ≥ 9 − для белков,

x₁ + 3 x ₂ ≥ 6 − для жиров,

x₁ + 8 x ₂ ≥ 8 − для углеводов,

2 x₁ + 4 x ₂ ≤ 16 − для нитратов.

Кроме того, по смыслу задачи должно выполняться условие

x₁ ≥ 0, x₂ ≥ 0.

Таким образом, экономико-математическая модель задачи примет следующий вид: составить рацион питания, при котором достигается минимум

целевой функции:

Z ( X ) = 80 x₁ + 10 x₂ → min

при ограничениях:

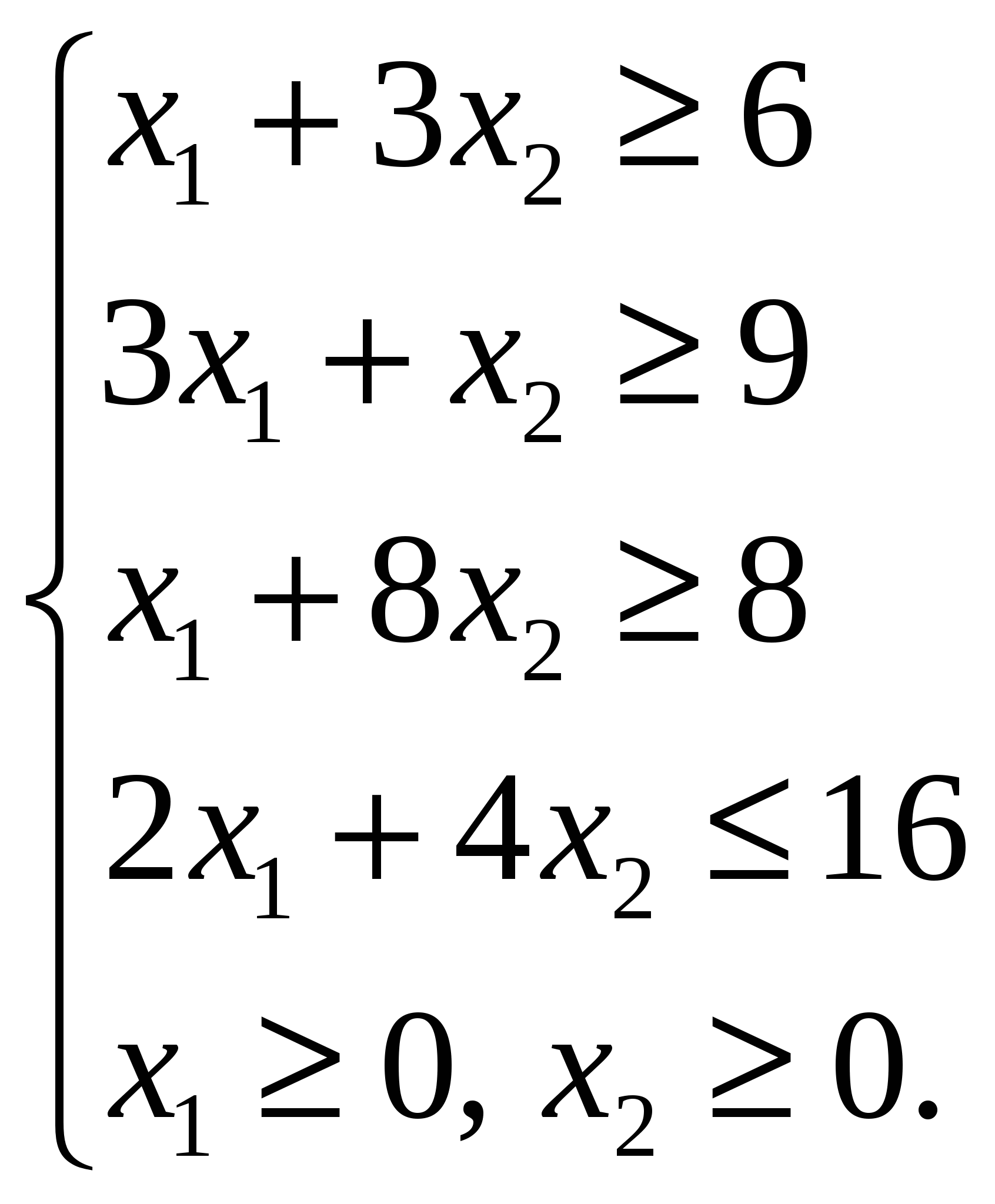(1.1)

Приводим систему линейных неравенств (1.1) к каноническому виду, вводя в каждое неравенство дополнительную неотрицательную переменную. Получим систему линейных уравнений:

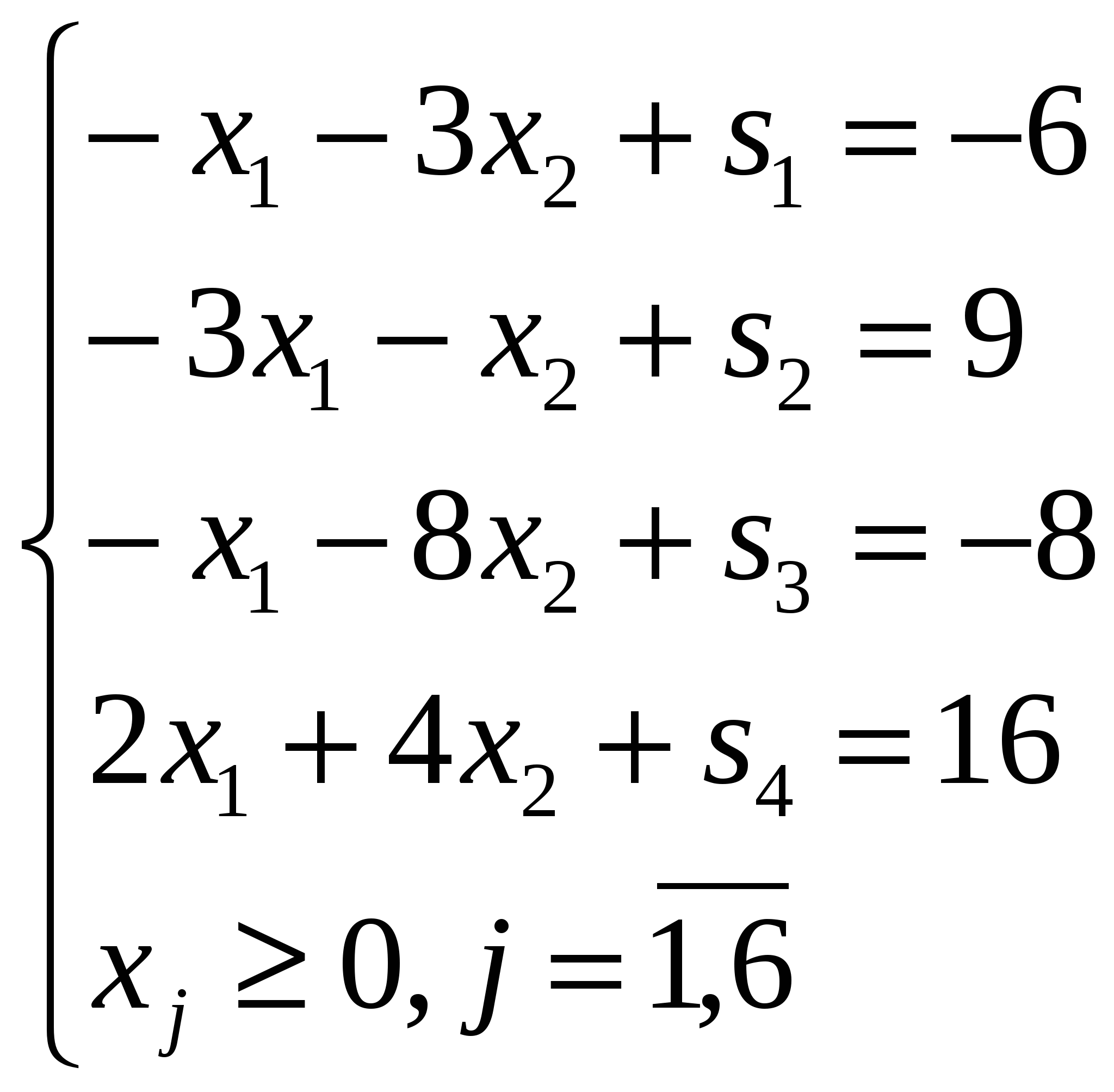(1.2)

Целевая функция будет иметь вид

Векторный анализ системы ограничений:

Расширенная целевая функция:

Вектора:

P0

P1(x1)

P2(x2)

P3(x3)

P4(x4)

P5(x5)

P6(x6)

-6

-1

-3

1

0

0

0

-9

-3

-1

0

1

0

0

-8

-1

-8

0

0

1

0

16

2

4

0

0

0

1

Базис:
Базисный вектор №1: x₃
Базисный вектор №2: x₄
Базисный вектор №3: x₅
Базисный вектор №4: x₆

Расширенная целевая функция:

При заполнении таблицы воспользуемся следующим алгоритмом:

Алгоритм симплекс-метода

1. Задача должна быть приведена к каноническому виду. Система ограничений приведена к единичному базису, т.е. разрешена относительно некоторых базисных переменных (не умоляя общности, будем считать, что относительно первых m переменных) с помощью метода Жордана – Гаусса. Получено соответствующее исходное опорное решение .

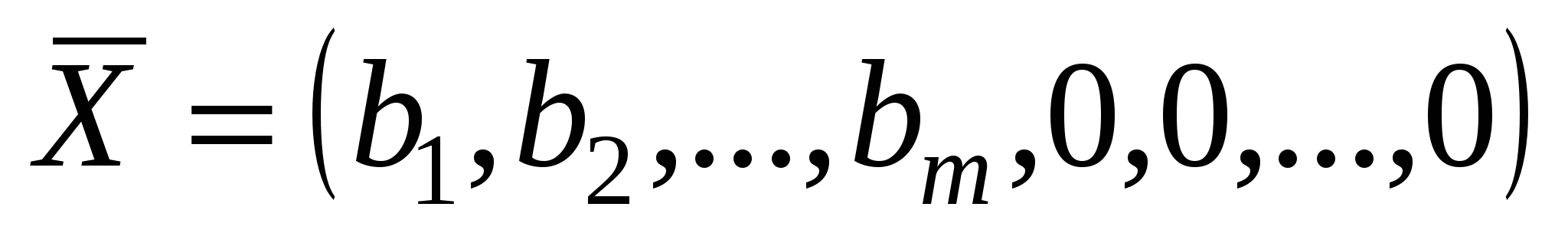2. Для удобства ведения вычислений записываем все в симплекс-таблицу (табл.). Столбец «Базис» содержит список базисных переменных; следующий столбец «c_j базиса» содержит коэффициенты целевой функции при базисных переменных; следующие столбцы содержат коэффициенты системы ограничений при соответствующих переменных; столбец «b_i» - столбец свободных членов системы ограничений. Последняя строка содержит симплекс – разности, рассчитанные по формуле и последняя ячейка содержит значение целевой функции 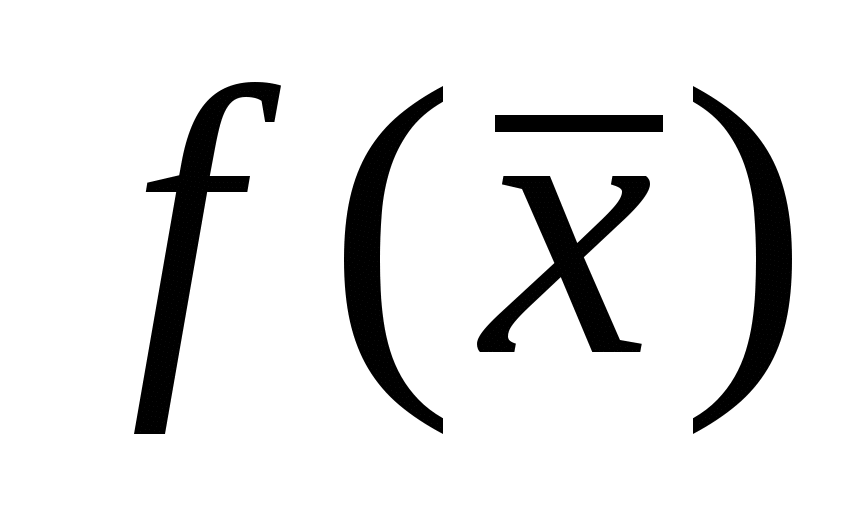=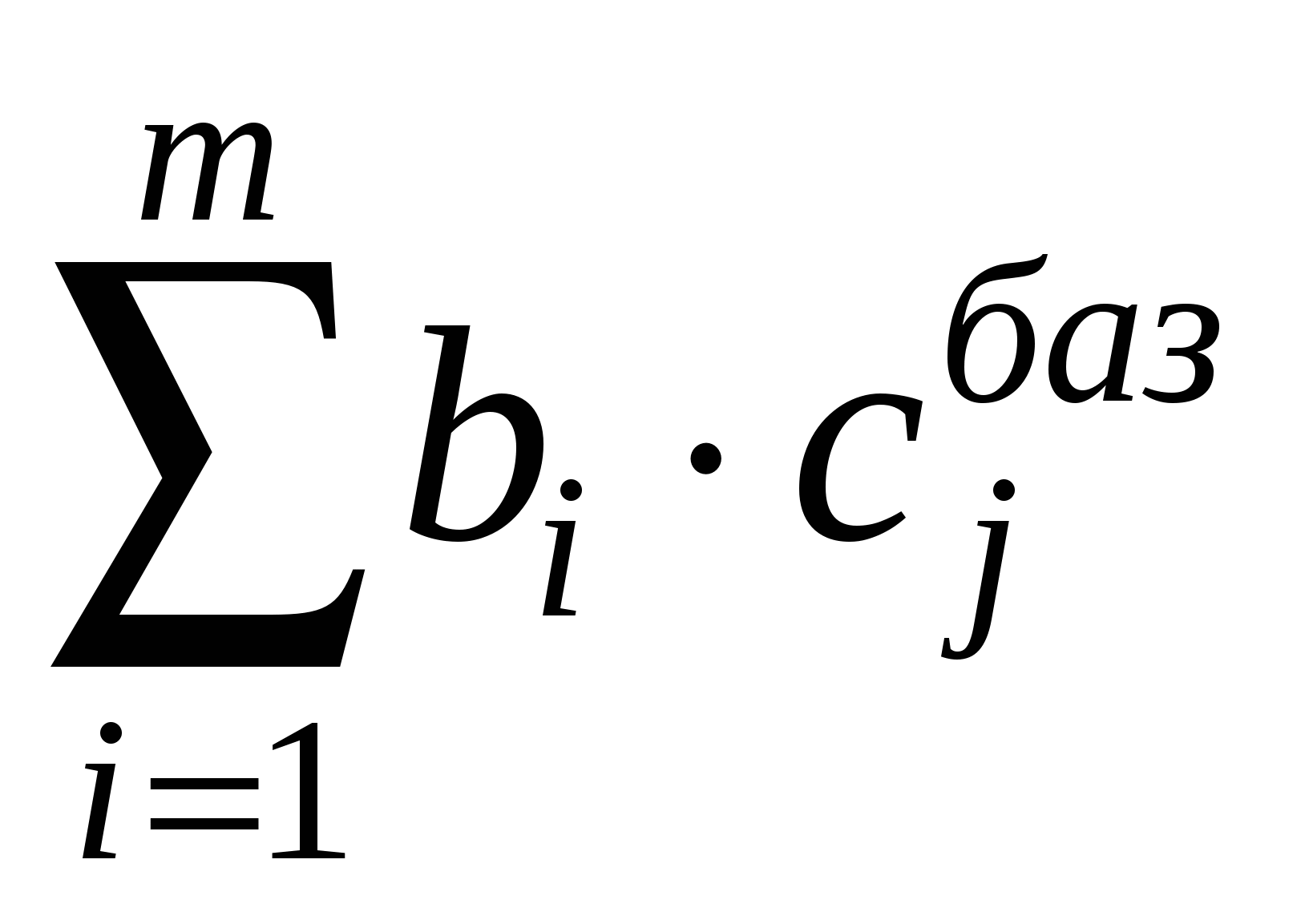. Отметим, что симплекс – разности базисных переменных всегда равны нулю.

Таблица

№

Базис

c_j базиса

с₁

с₂

…

с_m

c_m+1

…

c_n

b_i

x₁

x₂

...

x_m

x_m+1

…

x_n

1

x₁

с₁

1

0

0

2

x₂

с₂

0

1

0

…

…

…

…

…

…

…

…

…

…

…

…

m

x_m

с_m

0

0

1

…

…

3. Если все симплекс – разности неотрицательны, т.е. 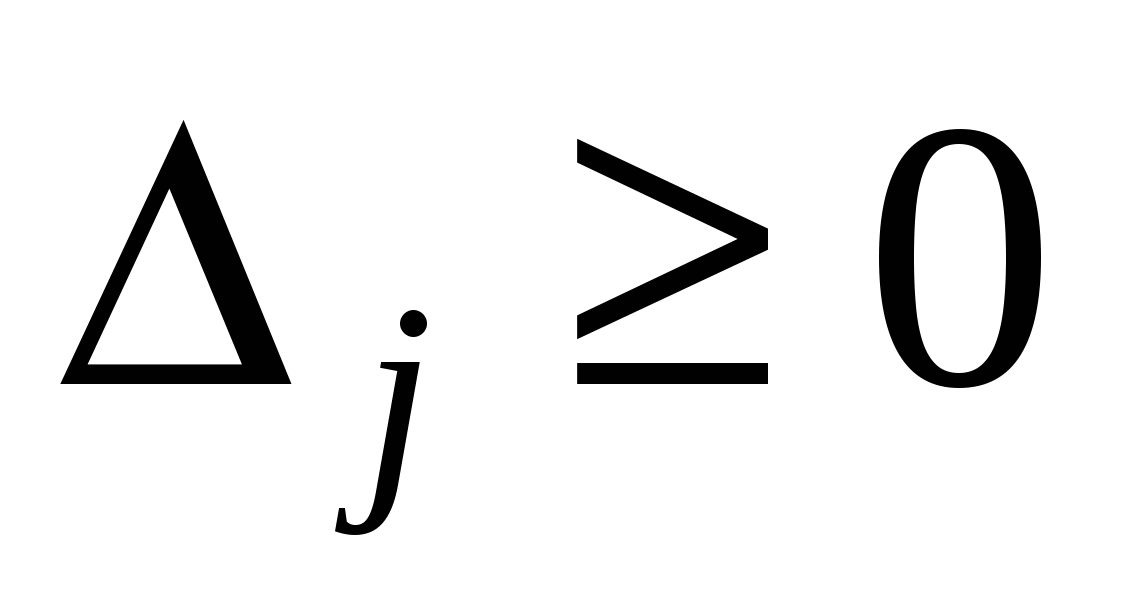, то опорный план оптимален.

4. Если хотя бы одна симплекс – разность отрицательна, 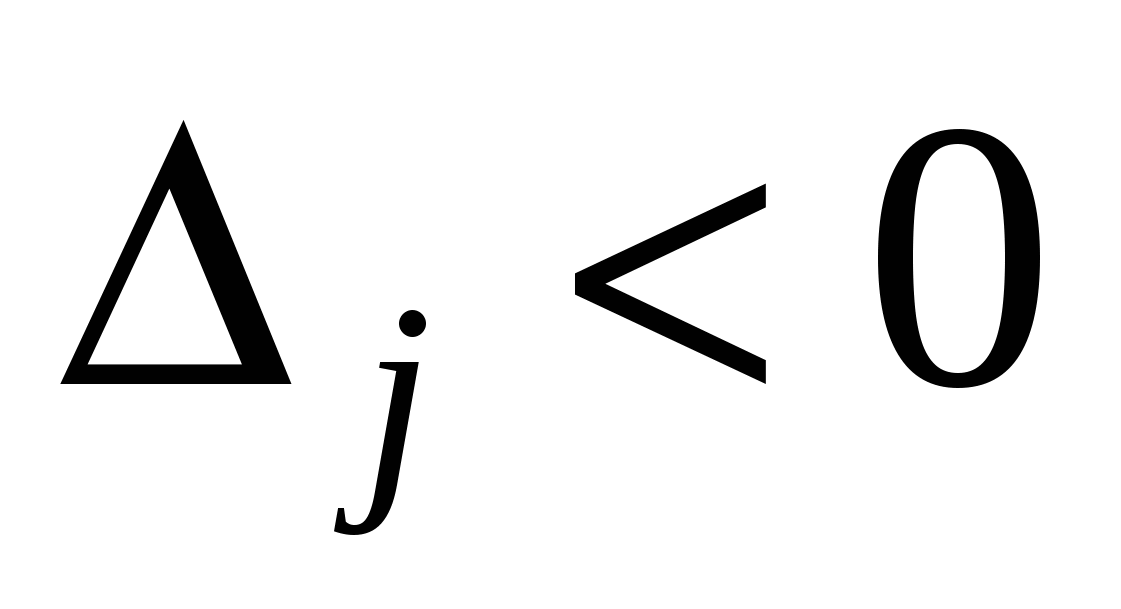, и в соответствующем столбце нет положительных элементов, то задача не имеет оптимального решения, т.е. .

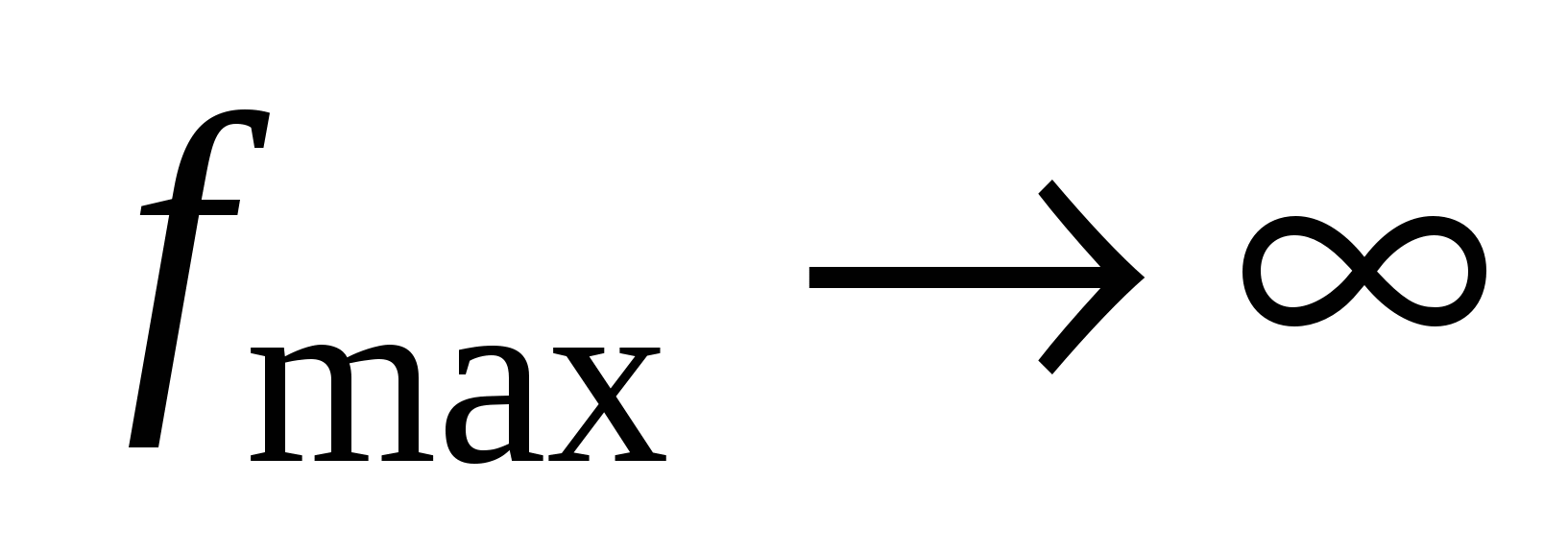5. Если хотя бы одна симплекс – разность отрицательна, 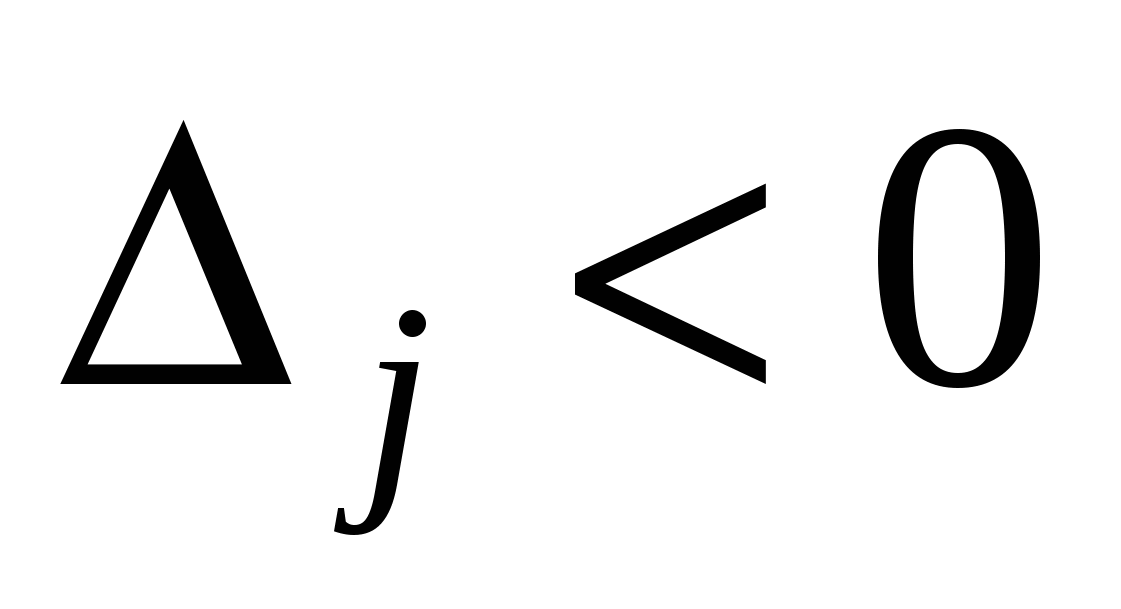, и в каждом столбце, имеющем отрицательную оценку, есть хотя бы один положительный элемент, то полученный опорный план можно улучшить.

6. Выбираем разрешающий столбец «р», которому соответствует наименьшая отрицательная оценка.

7. Выбираем разрешающую строку «к», которой соответствует наименьшее из отношений правых частей к соответствующим положительным элементам разрешающего столбца 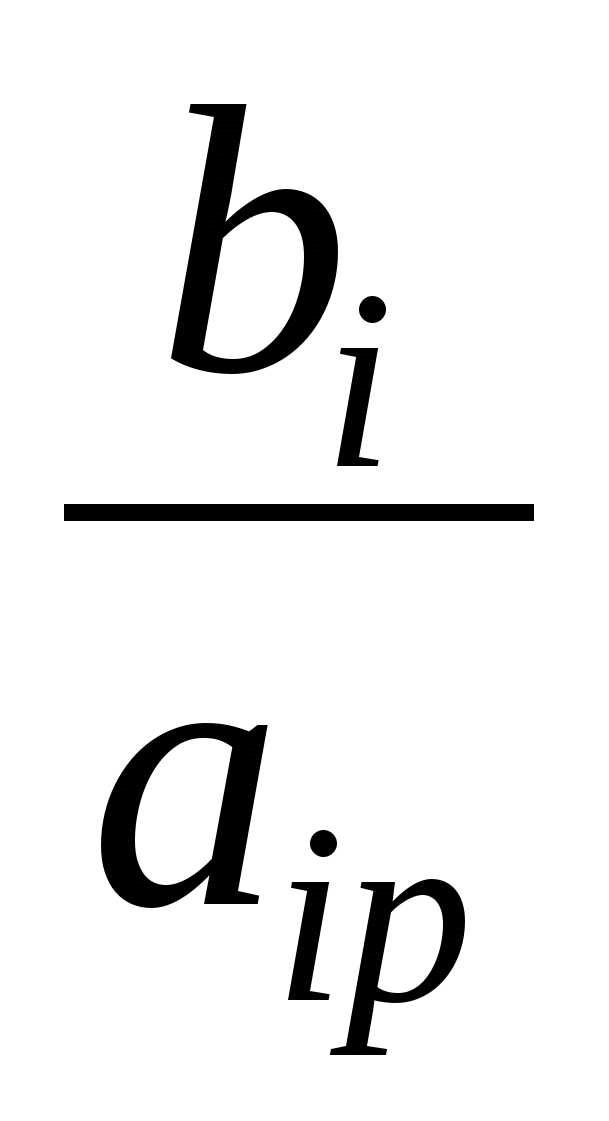. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки 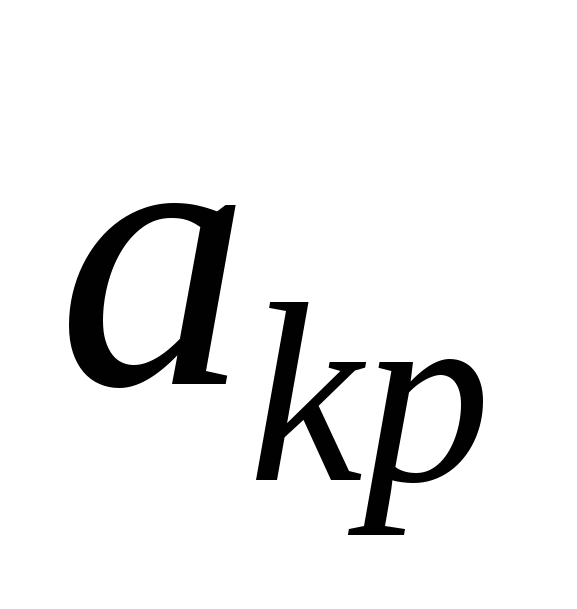называется разрешающим элементом.

8. Переходим к новой симплекс – таблице, в которой будет новый базис: базисная переменная на «к» - ом месте в старом базисе меняется на новую переменную 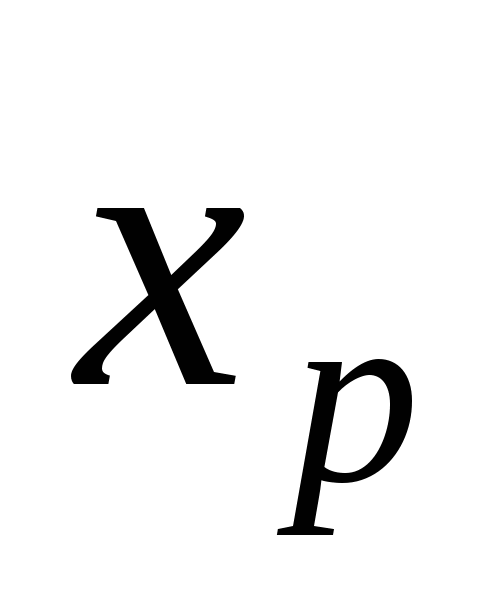. Соответствующий вектор новой базисной переменной нужно превратить в единичный. Для этого разрешающую строку делим на 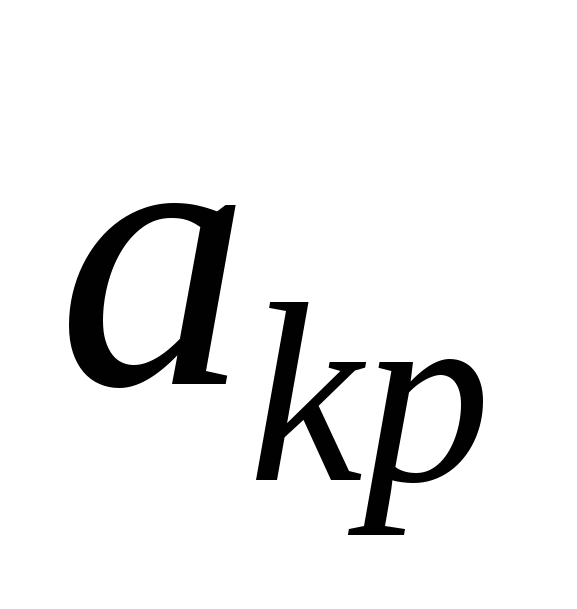, чтобы на месте разрешающего элемента появилась единица. Умножая разрешающую строку на подходящие числа и складывая её с остальными строками получаем нули в разрешающем столбце. После этого выписываем новый опорный план и пересчитываем строчку оценок. Переходим к пункту 3.

называется симплекс – разностью или оценкой.

Составляем симплекс – таблицу:

Таблица №1

№

Базис

c_j базиса

с₁=80

с₂=10

c₃=0

с₄=0

c₅=0

c₆=0

P0(b_i)

P1

P2

P3

P4

P5

P6

1

P3

0

-1

-3

1

0

0

0

-6

6

2

P4

0

-3

-1

0

1

0

0

-9

3

3

P5

0

-1

8

0

0

1

0

-8

8

4

P6

0

2

4

0

0

0

1

16

8

-80

-10

0

0

0

0

S min=0

Невозможно выбрать столбец замещения, так как нет положительных dj!
Выберем столбец таким образом. Чтобы избавиться от недопустимого решения, т.е. от отрицательных значений в столбце свободных членов (Р0).
Замещаемый базисный вектор: P3 (1-я строка)
Новый базисный вектор: P1 (1-й столбец)
Заменяем базисный вектор P3 на P1.
Таблица №2

№

Базис

c_j базиса

P0

80

10

0

0

0

0

P1

P2

P3

P4

P5

P6

1

P1

80

6

1

3

-1

0

0

0

2

P4

0

9

0

8

-3

1

0

0

3

P5

0

-2

0

-5

-1

0

1

0

4

P6

0

4

0

-2

2

0

0

1

S min =

480

0

230

-80

0

0

0

Замещаемый базисный вектор: P5 (3-я строка)
Новый базисный вектор: P2 (2-й столбец)
Заменяем базисный вектор P5 на P2.
Таблица №3

№

Базис

c_j базиса

P0

80

10

0

0

0

0

P1

P2

P3

P4

P5

P6

1

P1

80

4,8

1

0

-1,6

0

0,6

0

2

P4

0

5,8

0

0

-4,6

1

1,6

0

3

P2

10

0,4

0

1

0,2

0

-0,2

0

4

P6

0

4,8

0

0

2,4

0

-0,4

1

S min =

388

0

0

-126

0

46

0

Замещаемый базисный вектор: P4 (2-я строка)
Новый базисный вектор: P5 (5-й столбец)
Заменяем базисный вектор P4 на P5.

Таблица №4

№

Базис

c_j базиса

P0

80

10

0

0

0

0

P1

P2

P3

P4

P5

P6

1

P1

80

2,625

1

0

0,125

-0,375

0

0

2

P5

0

3,625

0

0

-2,875

0,625

1

0

3

P2

10

1,125

0

1

-0,375

0,125

0

0

4

P6

0

6,25

0

0

1,25

0,25

0

1

S min =

221,25

0

0

6,25

-28,75

0

0

Замещаемый базисный вектор: P6 (4-я строка)
Новый базисный вектор: P3 (3-й столбец)
Заменяем базисный вектор P6 на P3.
Таблица №5

№

Базис

c_j базиса

P0

80

10

0

0

0

0

P1

P2

P3

P4

P5

P6

1

P1

80

2

1

0

0

-0,4

0

-0,1

2

P5

0

18

0

0

0

1,2

1

2,3

3

P2

10

3

0

1

0

0,2

0

0,3

4

P3

0

5

0

0

1

0,2

0

0,8

S min =

190

0

0

0

-30

0

-5

Невозможно выбрать столбец замещения, так как нет положительных dj!
Получено оптимальное решение.

x1

x2

x3

x4

x5

x6

2

3

5

0

18

0

Из таблицы получим значения переменных целевой функции:

Целевая функция:
S min = 80·2+10·3
И в результате:
S min = 190;
Ответ: x₁=2; х₂=3- количество кормов I, II, входящих в рацион питания. Общая стоимость рациона (целевая функция) при котором достигается минимум целевой функции равен 190.

Решение задачи с помощью MS EXCEL

Для решения задач оптимизации в MS Excel используют надстройку Поиск решения, которая вызывается из пункта главного меню «Сервис» (рис. 1).

Если в версии Excel, установленной на Вашем компьютере, отсутствует данный подпункт меню «Сервис», необходимо вызвать пункт меню «Надстройки» и в предложенном списке дополнительных модулей выбрать «Поиск решения» (рис. 2).

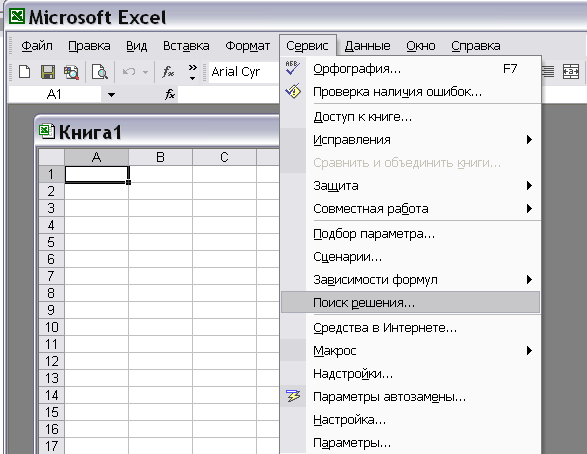
Рис. 1

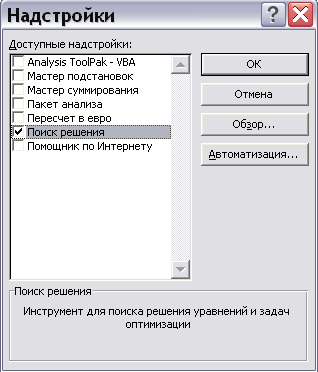
Рис. 2

Рассмотрим использование данной надстройки на примере. Решим с её помощью задачу, математическая модель которой строилась. Математическая модель задачи имеет вид:

целевой функции:

Z ( X ) = 80 x₁ + 10 x₂ → min

при ограничениях:

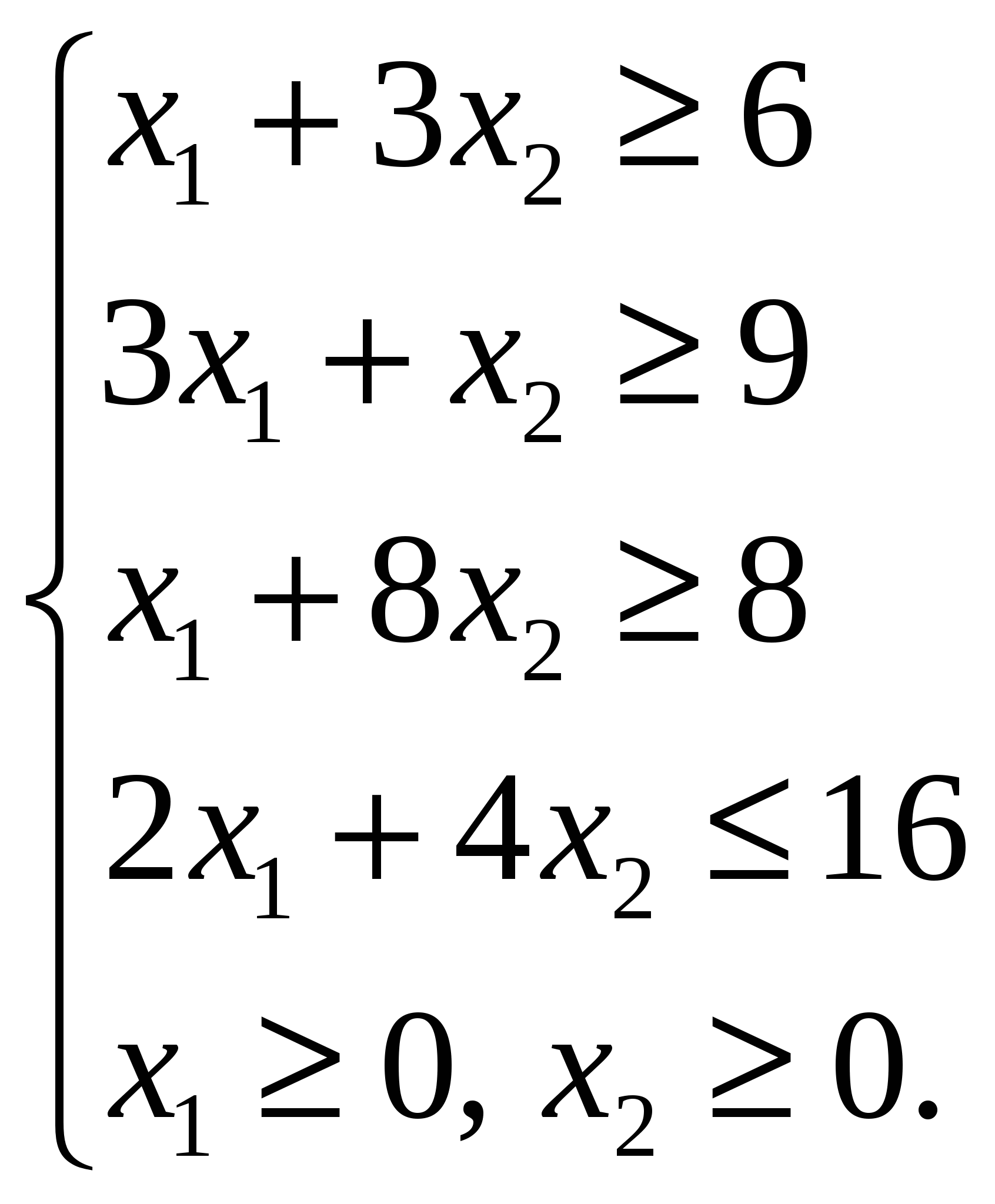Составим шаблон в редакторе Excel, как показано на рис. 3

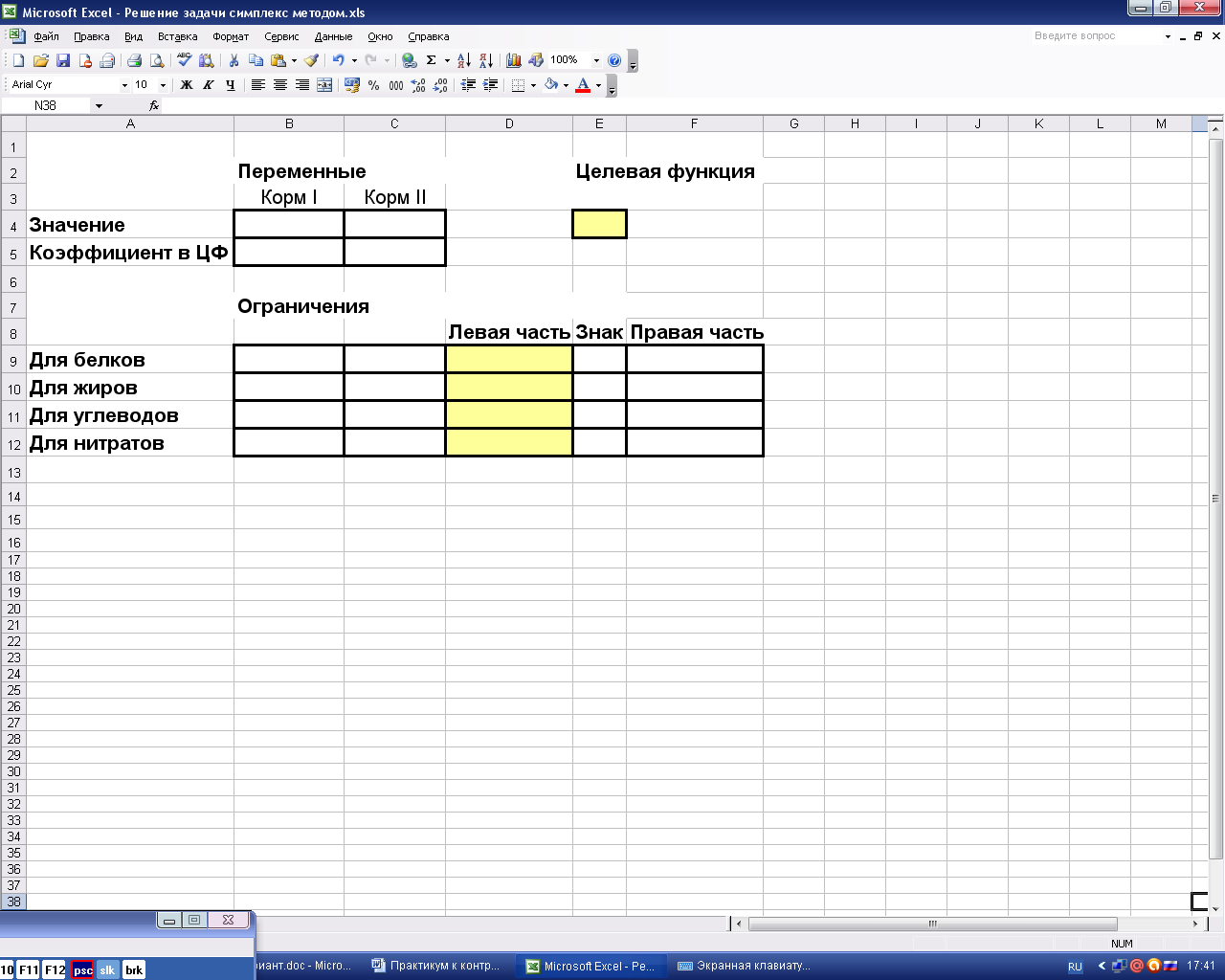
Рис.3. Шаблон оформления задачи

Теперь занесём данную в задаче числовую информацию (рис. 4).

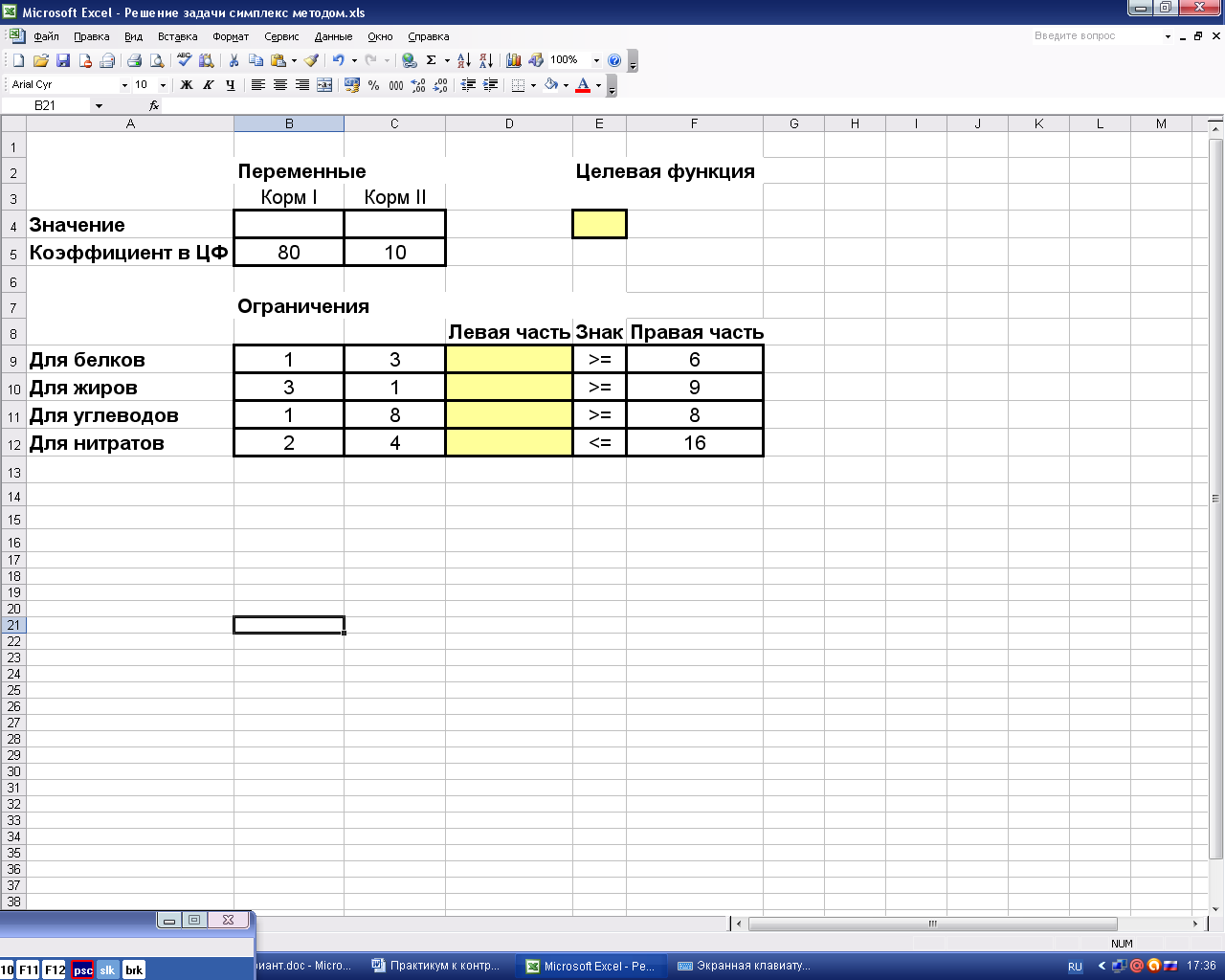
Рис.4. Исходные данные задачи

В выделенные пустые ячейки (значения целевой функции и левых частей неравенств) необходимо занести формулы, отображающие связи и отношения между числами на рабочем листе.

Ячейки B4 – С4 называются в Excel изменяемыми (в нашей модели это неизвестные переменные), т.е., изменяя их Поиск решения будет находить оптимальное значение целевой функции. Значения, которые первоначально вводят в эти ячейки, обычно нули (незаполненные клетки трактуются по умолчанию как содержащие нулевые значения).

Теперь необходимо ввести формулы. В нашей математической модели, целевая функция представляет собой произведение вектора коэффициентов на вектор неизвестных. Действительно, выражение можно рассматривать как произведение вектора (80,10) на вектор (Х₁,Х₂).

В Excel существует функция СУММПРОИЗВ, которая позволяет найти скалярное произведение векторов. В ячейку Е4 необходимо вызвать данную функцию, а в качестве перемножаемых векторов задать адреса ячеек, содержащих коэффициенты уравнений (в данном случае, это В5:С5) и ячеек, в которые в результате решения будут помещены значения Х₁ и Х₂ (ячейки В4:С4) (рис. 5).

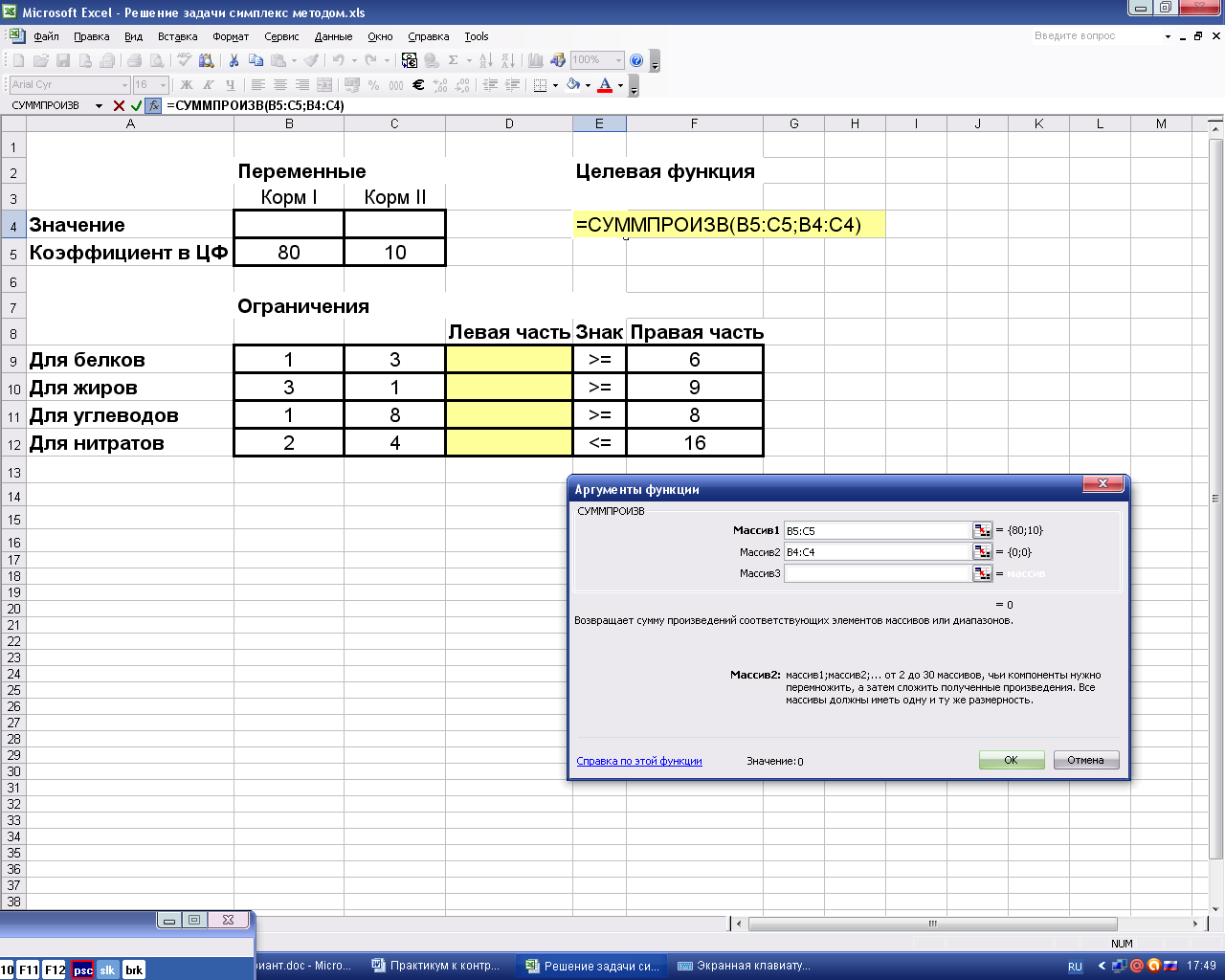
Рис.5. Вызов функции СУММПРОИЗВ.

Каждая левая часть ограничения тоже представляет собой произведение двух векторов: соответствующей строки матрицы затрат и вектора неизвестных. То есть, выражение Х₁+3Х₂ (для первого ограничения Х₁ + 3Х₂ 6) будем рассматривать как произведение вектора коэффициентов (1,3) и вектора переменных (Х₁,Х₂).

В ячейке, отведенной для формулы левой части первого ограничения (D9), вызовем функцию СУММПРОИЗВ. В качестве адресов перемножаемых векторов занесем адрес строки коэффициентов В9:С9 и адрес значений переменных В4:С4 (рис. 6).

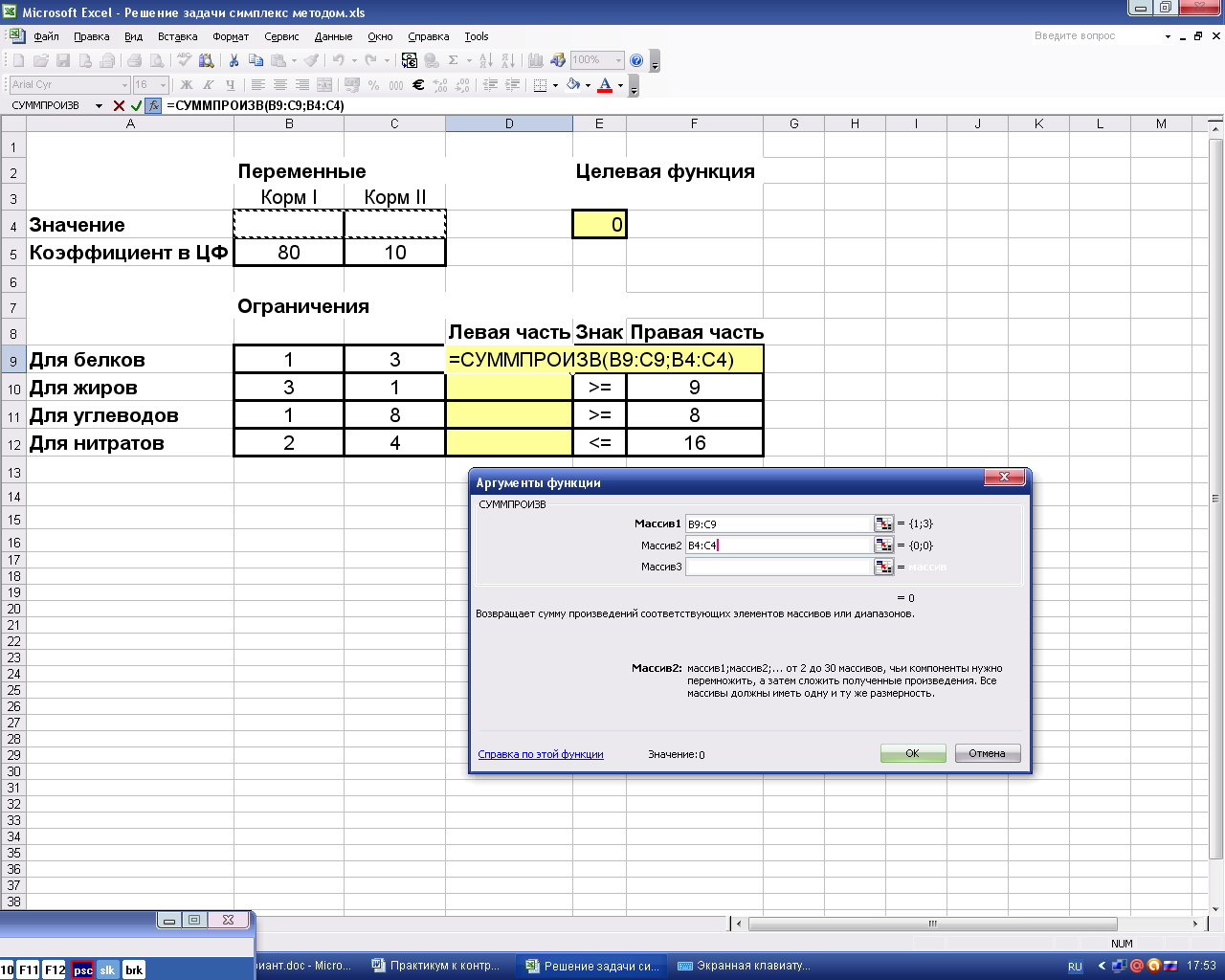
Рис.6

В четыре оставшиеся ячейки графы «Левая часть» вводим аналогичные формулы, используя соответствующую строку матрицы затрат. Фрагмент экрана с введёнными формулами показан на рис.7.

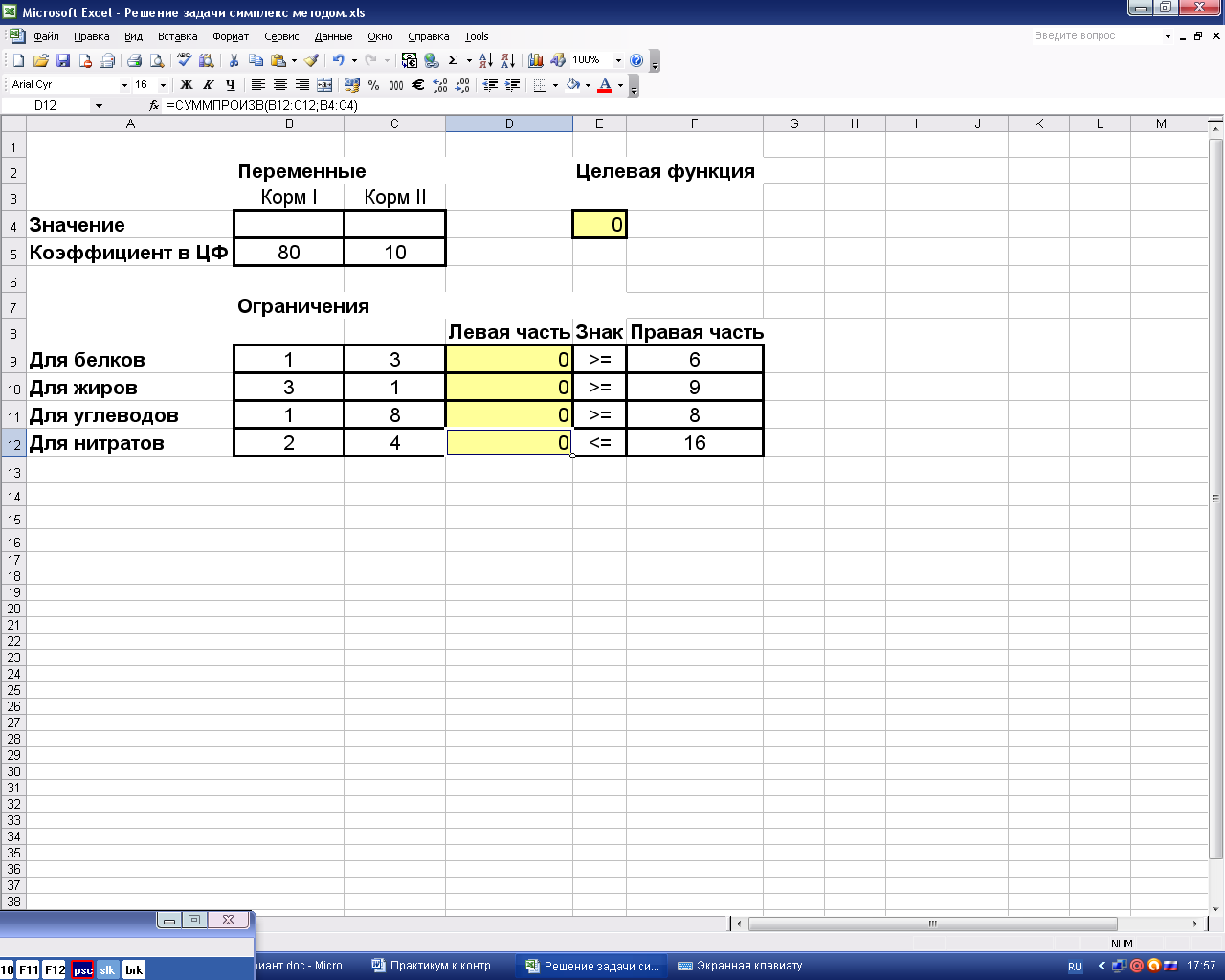
Рис.7

Важно, чтоб к моменту вызова сервиса «Поиск решения» на рабочем листе с задачей должны быть занесены формулы для левых частей ограничений и формула для значения целевой функции.

В меню Сервис выбираем Поиск решения. В появившемся окне задаём следующую информацию:

1. в качестве целевой ячейки устанавливаем адрес ячейки для значения целевой функции Е4;

2. «флажок» устанавливаем на вариант «максимальному значению», т.к. в данном случае, целевая функция дохода подлежит максимизации;

3. в качестве изменяемых ячеек заносится адрес строки значений переменных В4:С4;

4. справа от окна, предназначенного для занесения ограничений, нажимаем кнопку «Добавить», появится форма для занесения ограничения (рис. 8)

Рис.8 Форма для занесения одного ограничения ЗЛП

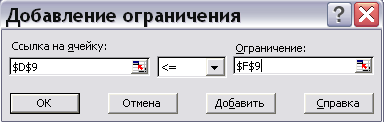
Рис.9 Занесение первого ограничения задачи

5. в левой части формы «Ссылка на ячейку» заносится адрес формулы для левой части первого ограничения D9, выбирается требуемый знак неравенства (в нашем случае, <=), в поле «Ограничение» заносится ссылка на правую часть ограничения F9 (рис. 9).

6. аналогично заносятся все ограничения задачи, после чего нажимается кнопка «ОК».

Таким образом, окно «Поиск решения» с занесенной информацией выглядит следующим образом (рис.10):

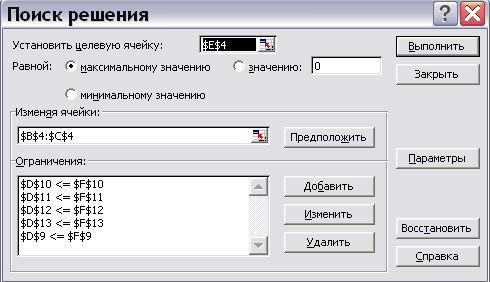
Рис.10.

Далее необходимо нажать кнопку Параметры, установить «флажки» «Линейная модель» и «Неотрицательные значения», поскольку в данном случае задача является ЗЛП, а ограничение 6) требует неотрицательности значений (рис.11).

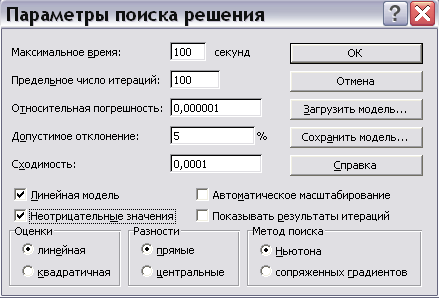
Рис.11 Установка параметров

Затем следует нажать «ОК», «Выполнить», после чего появляется окно результата решения (рис.12).

Рис.12. Окно результата решения

Если в результате всех действий получено окно с сообщением «Решение найдено», то Вам предоставляется возможность получения трех типов отчета, которые полезны при анализе модели на чувствительность. В данном примере достаточно сохранить найденное решение, нажав «ОК». В результате получено решение задачи из примера 1. (рис.13).

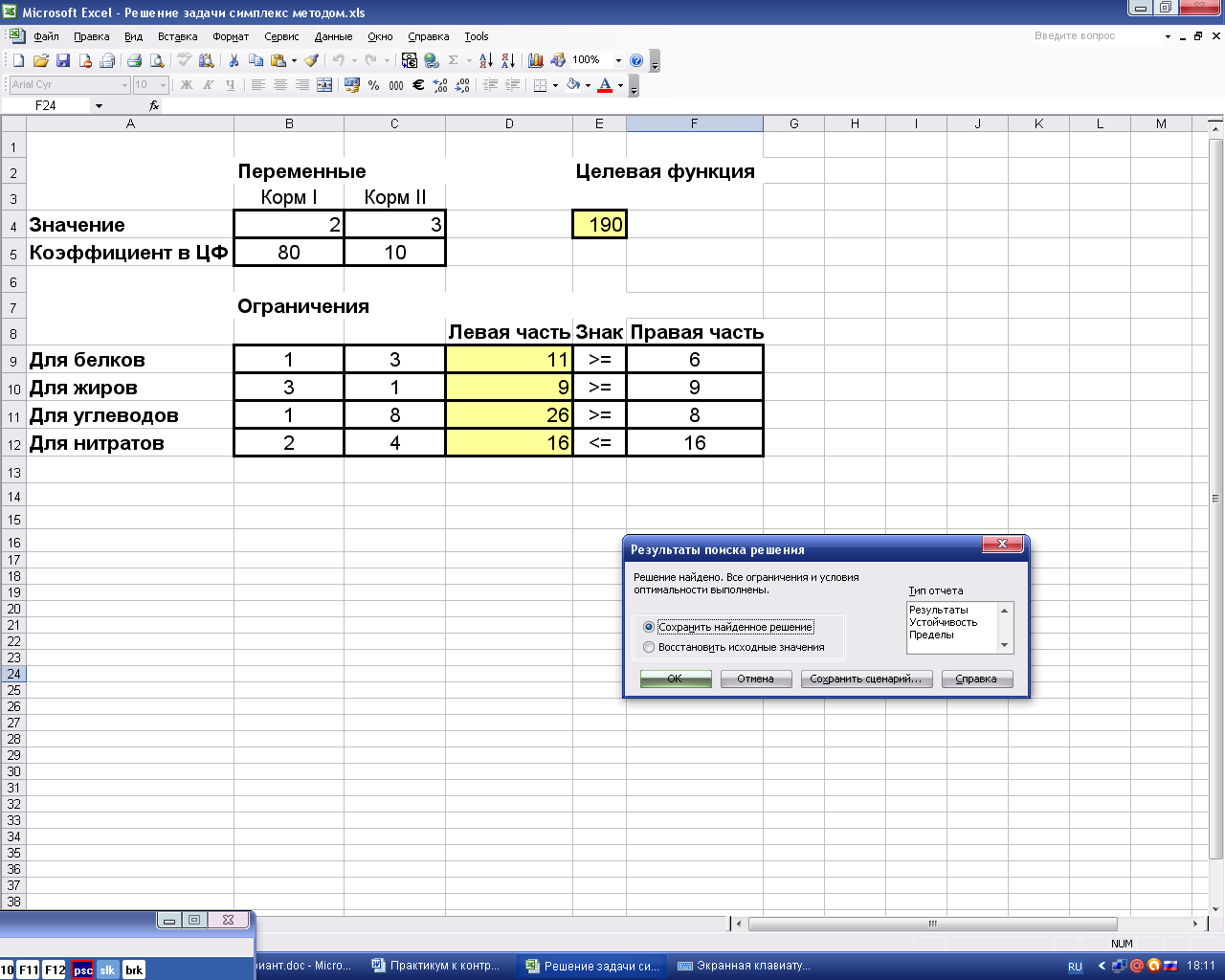
Рис.13 Результат применения «Поиска решения»

Если в результате решения задачи выдано окно с сообщением о невозможности нахождения решения (рис.14), это означает, что при оформлении задачи была допущена ошибка (не заполнены формулы для ограничений, неправильно установлен «флажок» максимизации/минимизации и т.д.).

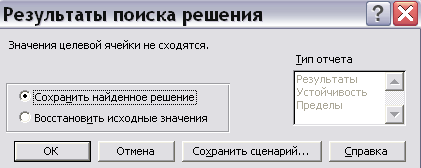
Рис.14. Сообщение об ошибке

В данном разделе рассмотрен общий формат решения задач оптимизации в Excel. В зависимости от экономических моделей, выполняют его соответствующие модификации.

Ответ: x₁=2; х₂=3- количество кормов I, II, входящих в рацион питания. Общая стоимость рациона (целевая функция) при котором достигается минимум целевой функции равен 190.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Высшая математика для экономистов / Под ред. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997.

2. Горчаков А.А., Орлова И.В. Компьютерные экономико - математические модели. – М.: Компьютер, ЮНИТИ, 1995.

3. Ерохин Н.М., Орехов Н.А., Сидоренко А.В. Статистические модели и планирование экспериментов в экономике: Методическое пособие. – Калуга: КФ МГТУ, 1994.

4. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М., 1997.

5. Исследование операций / Под ред. М.А. Войтенко и Н.Ш. Кремера. – М.: Экономическое образование, 1992.

6. Исследование операций в экономике: Учебное пособие для вузов / Н.Ш. Кремер, Б.А. Путко, И.М., И.М. Тришин, М.Н. Фридман; под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2004.

7. Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика. Математическое программирование. – Минск: Вышэйшая школа, 1994.

8. Математическое программирование / Под ред. Н.Ш. Кремера. – М.: Финстатинформ, 1995.

9. Орехов Н.А., Левин А.Г., Горбунов Е.А. Математические методы и модели в экономике: Учебное пособие для вузов / Под ред. проф. Н.А. Орехова. – М.: ЮНИТИ-ДАНА, 2004.

10. Орехов Н.А., Сахаров Г.В., Карпушин А.А. Введение в моделирование экономических процессов и явлений. – Калуга: КФ МГЭИ, 1997.

11. Сборник задач и упражнений по высшей математике: математическое программирование / Под ред. А.В. Кузнецова. – Минск: Высшая школа, 1995.

12. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001.