МОУ «Покровская вечерняя (сменная) общеобразовательная школа

Октябрьского района»

Информационные карты-задания в индивидуальном обучении.

Выполнила учитель математики

Сидорова Ирина Юрьевна

с. Покровка, 2008 г.

1.

В массовой школе процесс и содержание образования традиционно и органически связаны с классно-урочной системой. Вот уже более трехсот лет ею непреложно соблюдаются основные положения самой системы:

- опора на сенситивные возможности и особенности одновозрастной группы;

- однородность класса по уровню подготовленности;

- очное обучение в едином темпе и в условиях постоянного присутствия;

- урок- основная единица процесса и содержания обучения;

- в связи с незначительностью социального опыта учащийся заведомо ставится в позицию объекта воспитания.

Вечерняя школа не может опереться почти ни на один из названных признаков классно-урочной системы. Её учащиеся совершенно разнородны по возрастному составу, уровню подготовленности и социальному опыту. Педагоги нашей школы в качестве правила встречаются с тем, что в массовой школе является сбоем в классно-урочной системе. А именно:

- значительной дидактической запущенностью учащихся;

- утратой ( ослаблением, искажением) у них мотивации учебной деятельности.

Школа взрослых использует формы организации деятельности учащихся, присущие классно-урочной системе, и дополняет их специфическими, выходящими за классические рамки этой системы. Наряду с очной формой обучения она практикует очно-заочную форму, гораздо шире вечерняя школа использует форму индивидуального обучения.

Многие учащиеся нашей школы испытывают трудности в усвоении учебной программы из-за пробелов в знаниях, пропусков уроков по болезни и другим причинам, встречаются ученики со слабо развитой и кратковременной памятью. Все эти категории учащихся нуждаются в индивидуальном подходе. В учебной работе с этой частью контингента необходимо использовать такие формы работы, которые бы определяли посильность(доступность) заданий, восстанавливали бы учебные навыки и позитивную мотивацию к учебной деятельности, помогали бы ликвидировать пробелы в знаниях. Одной из форм помощи таким учащимся являются информационные карты по основным темам программы.

Карты могут использоваться учителем при объяснении нового материала. Они рассчитаны на быстрое восстановление в памяти учащихся пройденного материала- основной его теоретической части, а также на применение в решении задач и упражнений, в них дается план решения задачи на основе теоретической информации, приводятся образцы решения заданий. Большинство учащихся активно работает не с учебником, а с информационными картами. По карточке они проверяют себя, выполняя задания по образцу.

Карта помогает самостоятельно выполнить домашнее задание, служит хорошим подспорьем при подготовке к контрольной работе и зачету, при закреплении и обобщающем повторении материала в конце учебного года.

Ниже приведены образцы информационных карт по некоторым темам курса алгебры.

2.

9 класс.

РАЗЛОЖЕНИЕ КВАДРАТНОГО ТРЕХЧЛЕНА НА МНОЖИТЕЛИ.

Определение.

Квадратным трехчленом называется многочлен вида

ах²+bх+с,

где х-переменная, а,b,с-некоторые числа. Причем, а≠0.

Пример: х²+6х+2.

Если х₁ и х₂ –корни квадратного трехчлена ах²+bх+с,то

ах²+bх+с=а(х-х₁)(х-х₂).

Если квадратный трехчлен не имеет корней, то его нельзя разложить на множители.

Если квадратный трехчлен имеет один корень, то его можно разложить на множители:

ах²+bх+с=а(х-х₁)².

Образец 1.

Разложить квадратный трехчлен на множители: 7х²-14х+7.

Решение.

7х²-14х+7=0

х²-2х+1=0

D=4-4∙1∙1=0 (уравнение имеет один корень)

х==1

7х²-14х+7=7(х-1)².

Образец 2.

Разложить квадратный трехчлен на множители: 5х²+х-6.

Решение.

5х²+х-6=0

D=1-4∙5∙(-6)=121 (уравнение имеет два корня)

х₁=

х₂=

5х²+х-6=5(х-1)(х+)=( х-1)(5х+6).

Образец 3.

Разложить квадратный трехчлен на множители: х²+5х+10.

Решение.

х²+5х+10=0

D=25-4∙1∙10=25-40=-15<0, уравнение корней не имеет.

Значит, трехчлен нельзя разложить на множители.

Выполни самостоятельно.

Задание. Разложить на множители квадратный трехчлен.

1)5y²+2y-3; 3)6х²-13х+6.

2)-2x²+5x+7;

3.

9 класс.

ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ.

Построить параболу

y=ax²+bx+c.

1)Указать направление ветвей параболы.

Если а>0,ветви вверх,

если а<0,ветви вниз.

2)Найти абсциссу и ординату вершины параболы:

х₀=-, y₀=ax₀²+bx₀+c.

3)Ось симметрии х=х₀.

4)Заполнить таблицу:

х

х₀

у

у₀

5)Построить график.

Образец.

Построить график функции у=х²+2х+1.

Решение.

1)Графиком функции у=х²+2х+1 является парабола, ветви которой направлены вверх (а=1>0).

2) х₀=-.

у₀=(-1)²+2∙(-1)+1=1-2+1=0

3)Ось симметрии прямая х=-1.

4) Заполнить таблицу.

х

-4

-3

-2

-1

0

1

2

у

9

4

1

0

1

4

9

у(0)=у(-2)=0²+2∙0+1=1

у(1)=у(-3)=1²+2∙1+1=1+2+1=4

у(2)=у(-4)=2²+2∙2+1=4+4+1=9

Выполни самостоятельно.

Задание. Построить графики:

1. у=2х²+8х+2;

2. у=-х²+2х;

3. у=х²-4х+4;

4) у=х²-6х+9.

4.

9 класс.

АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ.

Арифметическая прогрессия.

Образец.

1.Запишите 2 следующих члена последовательности 3;6;9;…, если известно, что она является арифметической прогрессией.

Решение:

a_n+1=a_n+d

d=6-3=3-разность арифметической прогрессии.

Арифметическая прогрессия: 3, 6, 9, 12 , 15,…

2.В арифметической прогрессии найти а₁₅, если а₁=3,5; d=-2.

Решение:

a_n=a₁+(n-1)d

n=15

a₁₅=3,5+(15-1)∙(-2)=3,5-28=-24,5.

Ответ: a₁₅=-24,5.

3.Найти разность арифметической прогрессии, если а₅=15, а₁₃=47.

Решение:

a_n=a₁+(n-1)d

a₅=a₁+4d

a₁₃=a₁+12d

15= a₁+4d

47= a₁+12d

-32=-8d

d=4

Ответ: d=4.

Выполни самостоятельно.

1.Запишите 2 следующих члена последовательности:

2;4;6;…, если известно, что она является арифметической прогрессией.

2. В арифметической прогрессии найти а₁₇, если а₁=4,5; d=-3.

3. Найти разность арифметической прогрессии, если а₄=11, а₁₂=35.

5.

9 класс.

АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ.

Сумма n-первых членов арифметической прогрессии.

Образец.

1.Последовательность -16,-13,… является арифметической прогрессией.

Найдите сумму n-первых её членов, если n=6.

Решение:

S_n=-формула суммы n-первых членов арифметической прогрессии.

А₁=-16

n=6

S₆-?

S₆=

d=a₂-a₁=-13+16=3

a₆=a₁+(n-1)d= a₁+5d

a₆=-16+5∙3=-16+15=-1

S₆=

Ответ: S₆=-51.

2.Найдите сумму первых 12-ти членов арифметической прогрессии, в которой а₁=4, d=2.

Решение:

S_n=

а₁=4

d=2

n=12

S₁₂-?

S₁₂=

а₁₂=a₁+(n-1)d= a₁+11d

а₁₂=4+11∙2=26

S₁₂=

Ответ: S₁₂=180.

Выполни самостоятельно.

1.Последовательность -16,-13,… является арифметической прогрессией.

Найдите сумму n-первых её членов, если n=16.

2. Найдите сумму первых 12-ти членов арифметической прогрессии, в которой а₁=5, d=3.

6.

9 класс.

АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ.

Геометрическая прогрессия.

Образец.

1.Запишите 2 следующих члена последовательности1,,…, если известно, что она является геометрической прогрессией.

Решение.

b_n+1= b_n∙q

b₂= b₁∙q

q=; q=; q=.

1,-геометрическая прогрессия.

2.Последовательность (b_n)-геометрическая прогрессия.

Найдите b₈, если b₁=-2,q=3.

Решение.

b₁=-2,

q=3.

b₈=?

b_n= b₁∙q^n-1-формула n-го члена геометрической прогрессии.

n=8

b₈= b₁∙q^8-1= b₁∙q⁷

b₈= -2∙3⁷=-2∙19683=-39366.

Ответ: b₈=-39366.

Выполни самостоятельно.

1.Запишите 2 следующих члена последовательности1,, …, если известно, что она является геометрической прогрессией.

2.Последовательность (b_n)-геометрическая прогрессия.

Найдите b₄, если b₁=-3,q=2.

7.

9 класс.

БЕСКОНЕЧНО УБЫВАЮЩАЯ ПРОГРЕССИЯ.

Бесконечно убывающая геометрическая прогрессия-это геометрическая прогрессия, у которой │q│<1.

S=-сумма бесконечно убывающей геометрической прогрессии.

Пример:

4;2;1;-геометрическая бесконечно убывающая прогрессия.

2;-…- геометрическая бесконечно убывающая прогрессия.

Образец 1.

Доказать, что последовательность -9;-3;… является бесконечно убывающей геометрической прогрессией(б.у.г.п.).

Решение:

q== ││<1

│q│<1- б.у.г.п.

Образец 2.

Найдите сумму б.у.г.п. 1;

Решение:

q==

S=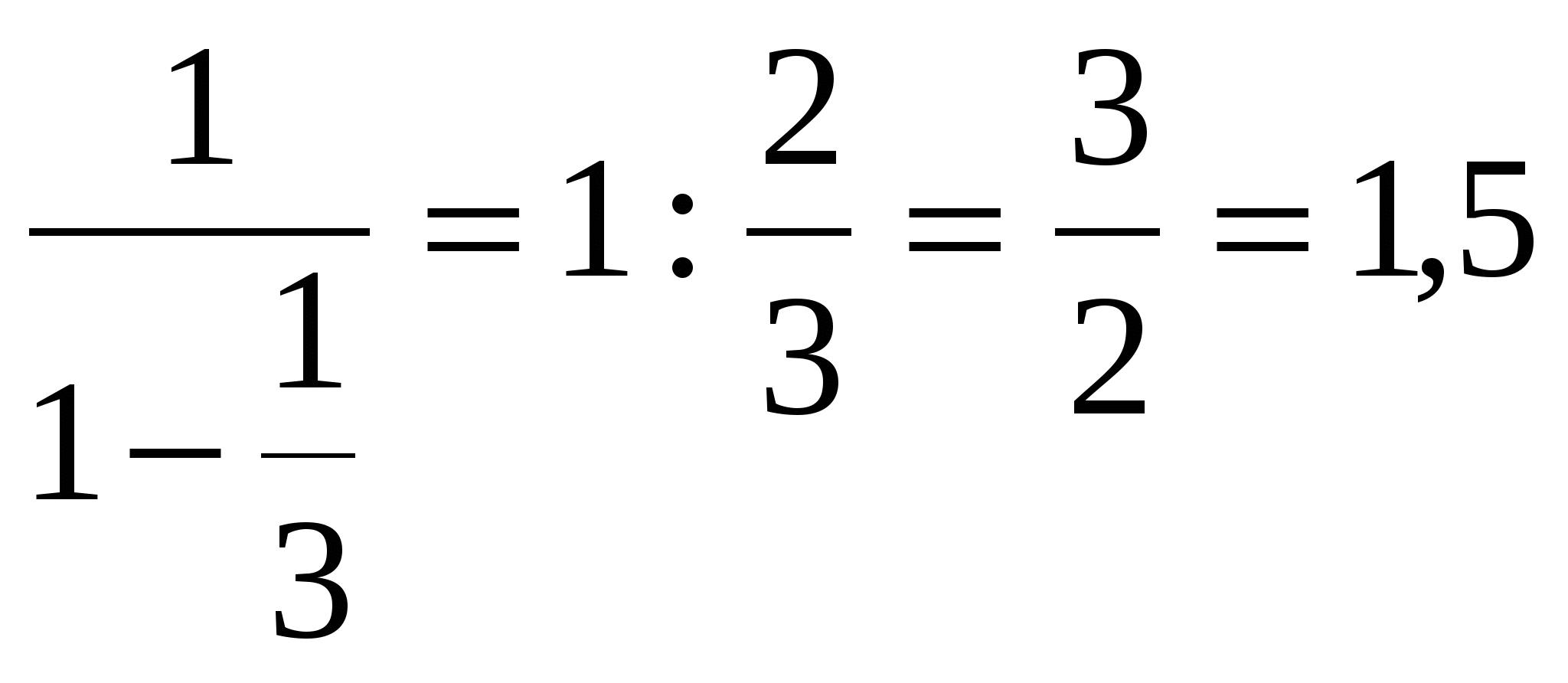

Ответ: S=1,5.

Образец 3.

Представьте в виде обыкновенной дроби число 0,(36).

Решение:

0,(36)=0,36+0,0036+0,000036+…

q==; │0,01│<1.

S=

Ответ:

Выполни самостоятельно.

1. Доказать, что последовательность 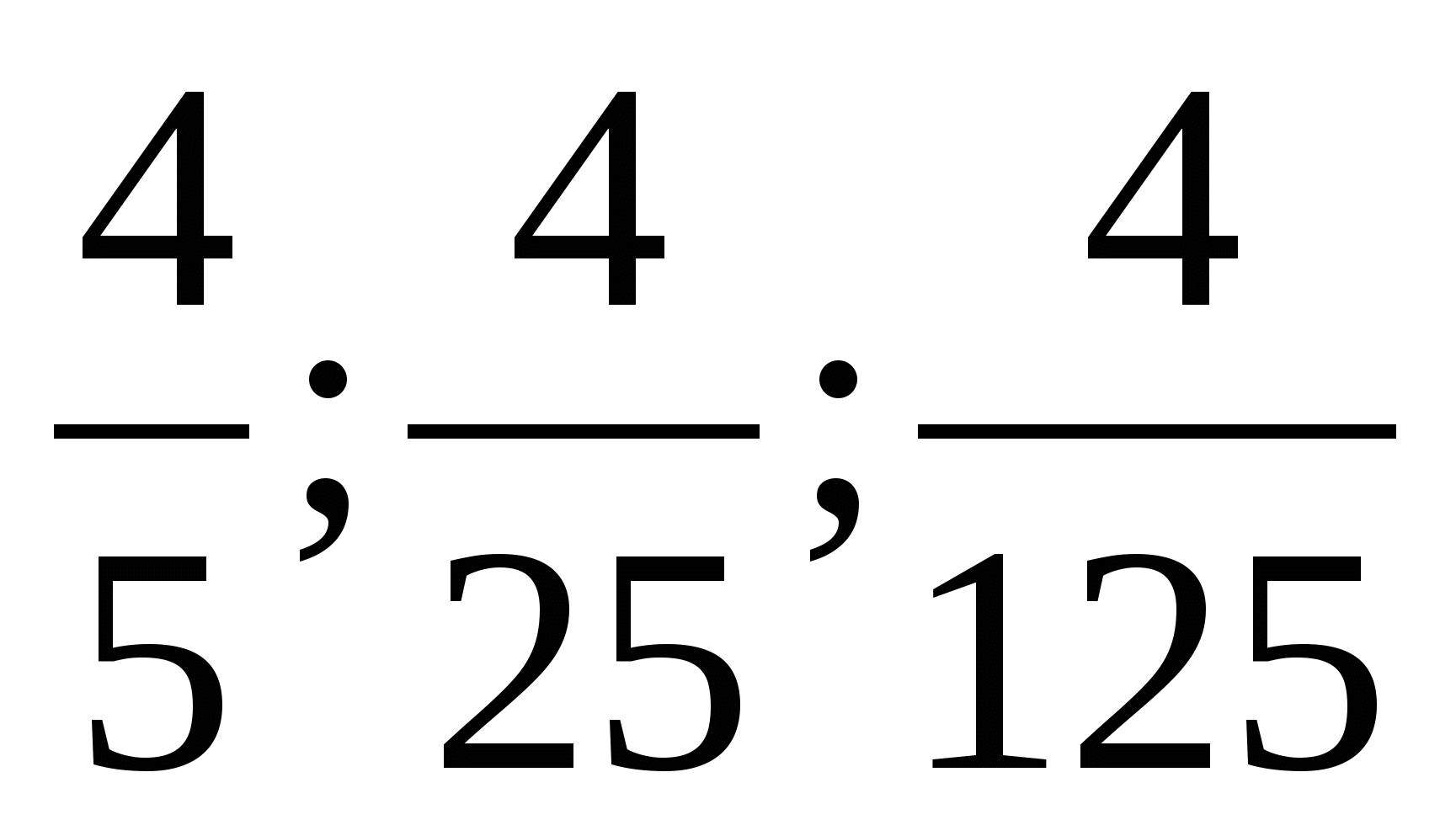;… является бесконечно убывающей геометрической прогрессией.

2. Найдите сумму б.у.г.п.

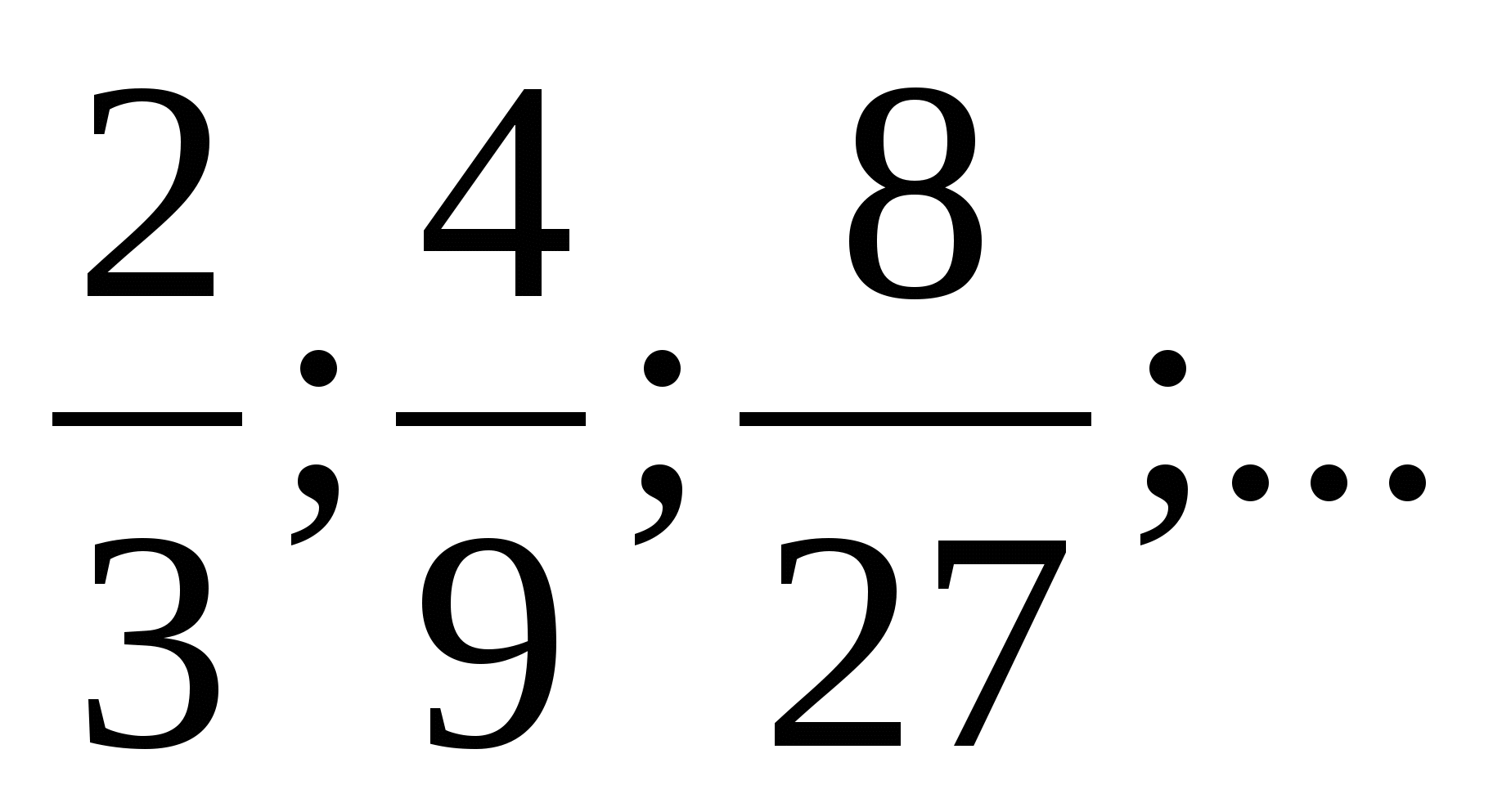
3)Представьте в виде обыкновенной дроби число а) 0,(6); б) 0,(81).

8.

11 класс.

ОСНОВНЫЕ СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ.

sin²x+cos²x=1

tgx∙ctgx=1

1+tg²x= 1+ctg²x=

Образец:

1) Вычислите cosα, tgα, ctgα, если sinα= и .

Решение:

sin²α+cos²α=1

cosα=±

cosα=±;

так как -II четверть, то cosα<0, значит cosα=-.

tgα=; tgα= .

ctgα= ctgα=-.

Ответ: cosα=-; tgα=-; ctgα=-.

2)Упростить выражение:

sin²α+2cos²α-1= sin²α+ cos²α+ cos²α-1=1+ cos²α-1= cos²α.

Выполни самостоятельно:

1. Зная,что

sinα=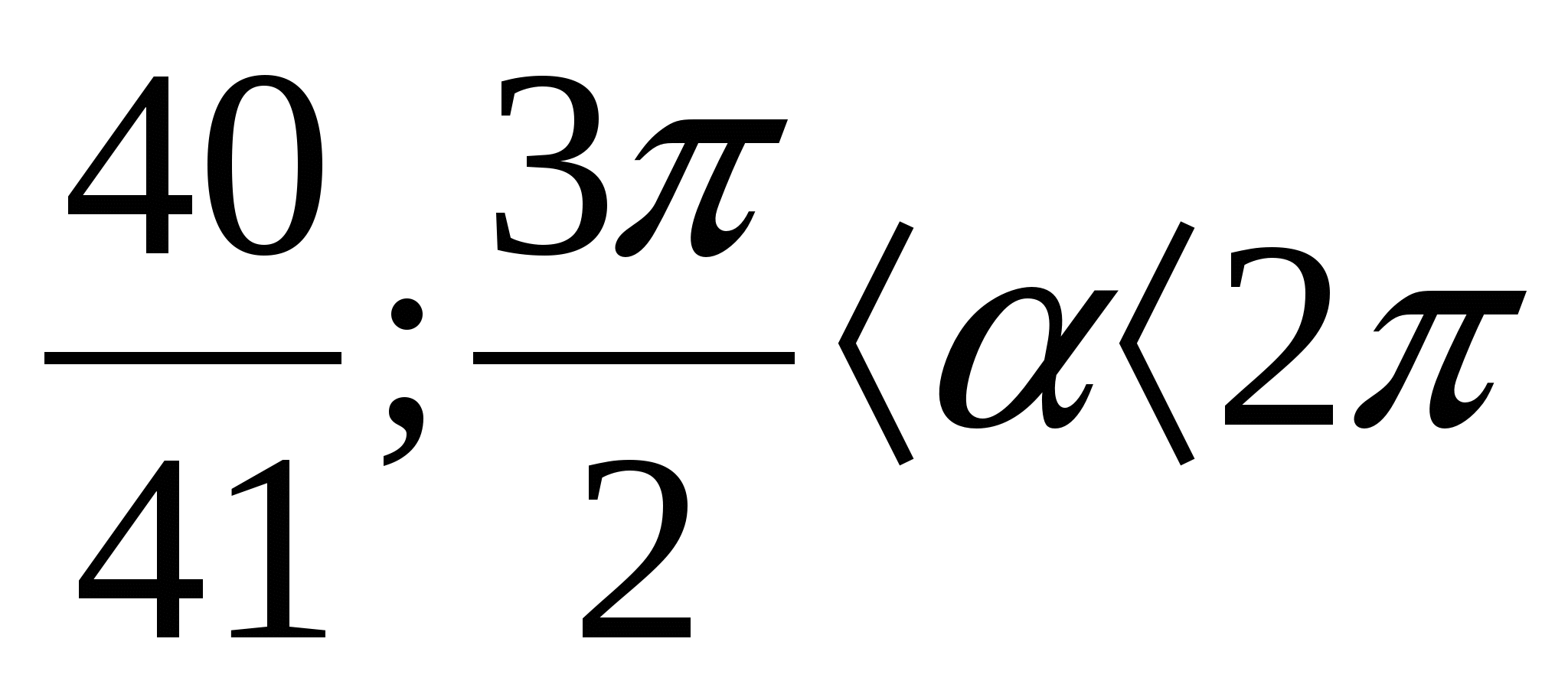, найти cosα, tgα, ctgα.

2)Упростите выражения:

а) (1-sinα)(1+ sinα)

б)

в)sinα∙cosα∙tgα.

9.

11 класс.

Решение простейших тригонометрических уравнений.

Уравнения вида sinx=a, cosx=a ( где│а│≤1) решаются по формулам.

sinx=a

x=(-1)ⁿ arcsina +n, n Z;

cosx=a

x= arccosa +2n, n Z.

Образец 1. sin3x=

3х=(-1)ⁿ arcsin +n, n Z;

3х=(-1)ⁿ +n, n Z; ( Поделим все части уравнения на 3)

х=(-1)ⁿ +, n Z. Ответ:(-1)ⁿ +, n Z.

Реши самостоятельно: а) sin5x=; б) sin4x=.

Образец 2. cos2x=

2х= arccos +2n, n Z;

2х= + 2n, n Z; ( Разделим обе части уравнения на 2)

х=+n, n Z; Ответ: +n, n Z;

Реши самостоятельно: а) cos5x=; б) cos9x=.

Если в уравнениях sinx=a, cosx=a вместо а стоят числа 0,1,-1, то запись решения уравнений имеет особую форму.

Особая форма записи решений уравнений sinx=a, cosx=a.

sinx=1

х=+2n, n Z

sinx=-1

х=-+2n, n Z

sinx=0

х=n, n Z

cosx=1

х=2n, n Z

cosx=-1

х=+ 2n, n Z

cosx=0

х= +n, n Z

Образец 3. sin6x=1

6х=+2n, n Z

х=+ , n Z

х=+, n Z Ответ: +, n Z.

Реши самостоятельно:

а) sin4x=-1; б) sin3x=0; в) sin10x=1; г) cos3x=1; д) cos5x=-1; е) cos7x=0.