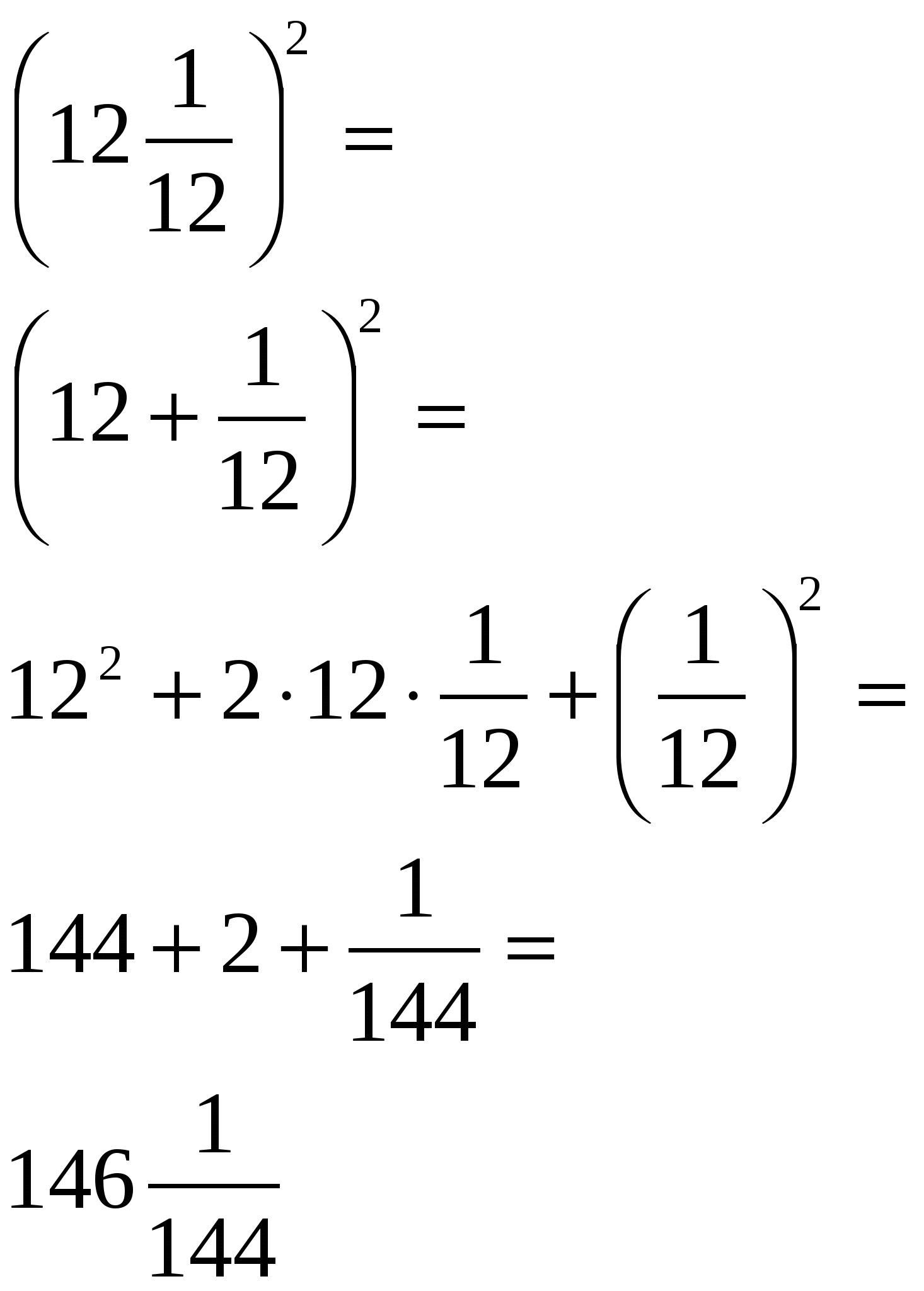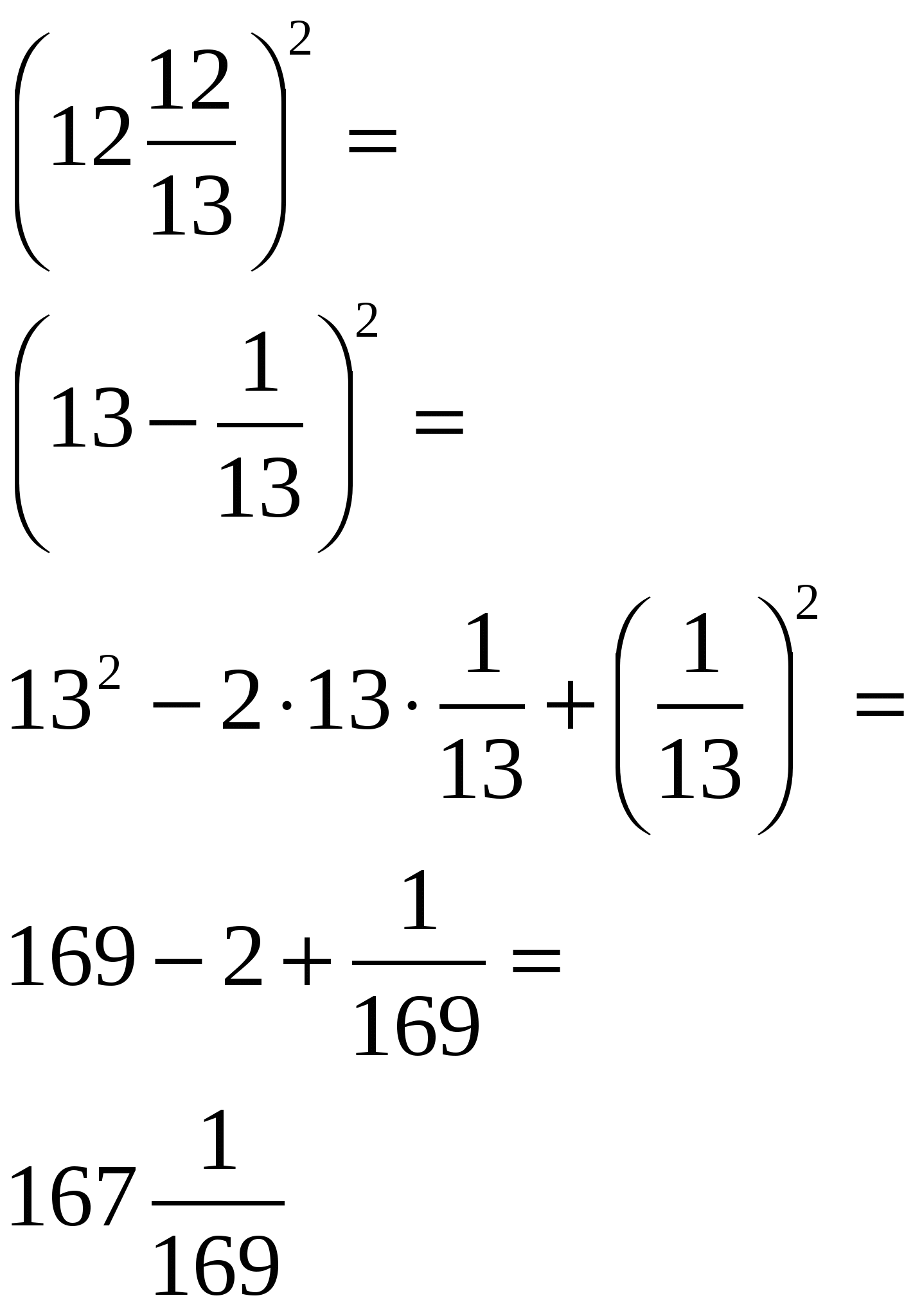Конспект урока на тему "Формулы сокращенного умножения. Квадрат суммы и квадрат разности"
Урок математики
Формулы сокращенного умножения.
Квадрат суммы и квадрат разности.
(конструирование урока
с использованием технологии УДЕ)
Составитель: Агринская Л.Ф.,
учитель МБОУ СОШ № 27 г.о. Самара
Не бойтесь формул! Учитесь владеть этим тонким инструментом человеческого гения! В формулах увековечены ценнейшие достижения людского рода, в них заключено величие и могущество разума, его торжество над покоренной природой.
Из книги “Машина“ под редакцией акад. И.И.Артоболевского
Дата проведения урока: 13.12.2013 г.
Тип урока: комбинированный
Цель урока: выработать у учащихся умение применять формулы (a±b)2= a2± 2ab+b2 как “слева направо”, так и “справа налево” в преобразованиях целых выражений в многочлены и в разложении многочленов на множители.
Цели ученика: запомнить формулы (a±b)2= a2± 2ab+b2, уметь читать выражения, т.е. переходить от формул к их словесному выражению и наоборот, научиться применять эти формулы при выполнении упражнений, самостоятельно составлять задания.
Средства обучения: приемы технологии УДЕ, презентация Power Point
Оборудование урока: ноутбук, проектор, экран.
Местоположение урока в планировании
Всего на изучение темы: “Многочлены. Арифметические операции над многочленами” согласно тематическому планированию отводится 22 часа. Данный урок является в параграфе 17 первым, при изучении пункта учебника “Формулы сокращенного умножения”. К этому моменту учащиеся умеют умножать многочлен на одночлен, многочлен на многочлен.
Структура урока:
Организационный момент (2 мин).
Актуализация опорных знаний учащихся (5 мин).
Самостоятельная работа.
Проверка домашнего задания.
Изучение нового материала (5 мин).
Закрепление пройденного (12 мин).
Физкультминутка (1 мин).
Самостоятельная работа (10 мин).
Постановка домашнего задания (2 мин).
Подведение итогов (2 мин).
Рефлексия (1 мин).
Конспект урока алгебры в 7 классе
(учебник А.Г. Мордковича, методика П.М. Эрдниева)
Организационный момент.
Актуализация знаний учащихся.
1.Самостоятельная работа.
Запишите
a и b
0,5a и 2b
a и 2b2
-ba и (-2b2)
1
Квадрат одночлена
a2 и b2
2
Удвоенное произведение одночленов
2ab
3
Разность квадратов одночленов
a2 - b2
4
Квадрат суммы одночленов
(a + b)2
Проверку осуществляют консультанты (4чел.) по готовым ответам, сообщают результаты, какие ошибки были допущены.
2. Проверка домашнего задания.
№ 461-467(г) (устно)
В этих упражнениях нужно было выполнить умножение двучлена на себя, сравнить результат и исходное выражение, сделать вывод.
(с+8)2= c2+16c+64
(-m-10)2 = m2+20m+100
(7y+6)2 = 49y2+84y+36
(10z+3t)2 =100z2+60zt+9t2
(m-n)2= m2-2mn+n2
(12-p)2 = 144-24p+p2
(7y-6)2 = 49y2-84y+36
(-3m+4n)2= 9m2-24mn+16n2
Изучение нового материала.
Сделали вывод, что в некоторых случаях умножение многочленов можно выполнить короче, воспользовавшись формулами сокращенного умножения.
(a+b)2=
=(a+b)(a+b)=
=(a+b)a+(a+b)b=
=a2+ab+ab+b2=
=a2+2ab+b2
(a-b)2=
=(a-b)(a-b)=
=(a-b)a-(a-b)b=
=a2-ab-ab+b2=
=a2-2ab+b2
Объединяя эти две формулы, мы можем записать совместно два тождества.
Тождеством называется равенство верное при любых значениях переменных.
(a±b)2= a2±2ab+b2
Ч итая эти тождества слева направо, получаем формулы сокращенного умножения
итая эти тождества слева направо, получаем формулы сокращенного умножения
(2x+3)2=4x2+12x+9
(7y-6)2=49y2-84y+36
(a±b) (a±b)= a2±2ab+b2
Читая данные тождества справа налево, получаем формулы разложения многочлена на множители
(2x+3)(2x+3)= 4x2+12x+9
(7y-6) (7y-6)= 49y2-84y+36
Квадрат ![]() двух чисел (a±b)2 равен трехчлену, состоящему из слагаемых:
двух чисел (a±b)2 равен трехчлену, состоящему из слагаемых:
1) квадрата первого числа (a2);
2) ![]() удвоенное произведение первого числа на второе (±2ab);
удвоенное произведение первого числа на второе (±2ab);
3) плюс квадрат второго числа (b2).
Геометрический смысл формулы
(a+b)2= a2+2ab+b2 для положительных чисел a и b
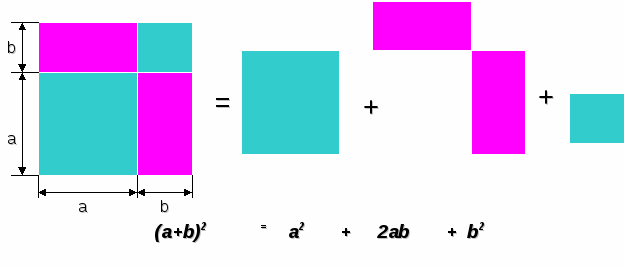
Геометрический смысл формулы (a-b)2 = a2-2ab+b2 для положительных чисел a и b, удовлетворяющих условию a > b
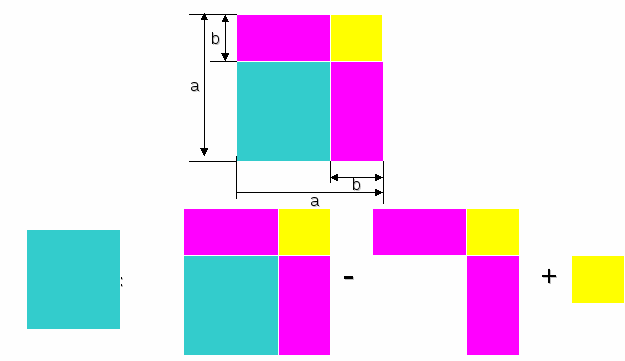
(a-b)2 = a2 - 2ab + b2
Схема
(a+b)2

a2+2∙a∙b+b2
x2 + + 9 6x
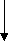
x 2 2 + + 32
2 + + 32 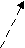
 ∙3∙x
∙3∙x
 (x+3)2
(x+3)2
Закрепление
Формулы квадрата суммы и квадрата разности можно представить с помощью геометрических фигурок следующим образом:
(□ ± Δ)2 = □2 ± 2∙□∙Δ+ Δ2
Эти фигурки изображают “окошечки”, куда можно вписать различные одночлены, чтобы понять и запомнить эти формулы.
Заполните таблицу по образцу
□
Δ
(□ + Δ)2
□2 + 2∙□∙Δ+ Δ2
Результат упрощения
2a
6
(2а+6)2=
(2a)2+2∙(2a)∙6+(6)2=
=4a2+24a+36
3а
-9
(3а-9)2=
(3a)2+2∙(3a)∙(-9)+(-9)2=
=9a2-54a+81
(3а+b)2=
(4а-b)2=
(а-5b)2=
(a2+2b3)2=
(3a-2b2)2=
Восстановите пропущенные выражения
25-10b2+b4 =(▭-▭)∙(▭-▭)=(▭-▭)2
25±10b2+b4 =(▭±▭)2
б) ▭+14е +е2 = 72+2∙▭∙е +е2
(▭-▭)2= 49-▭+е2
(▭±▭)2 = 49±14е +е2
Выполните сокращение дробей, запишите пропущенные выражения; проверьте ответ умножением многочленов:
2
5+ 10а+а2 = ▭ = ▭
5+а
25- 10а+а2 = ▭ = ▭
5
Используя формулы (a±b)2, вычислите по аналогии
![]()
![]()
Образец:
а ) б)
) б)
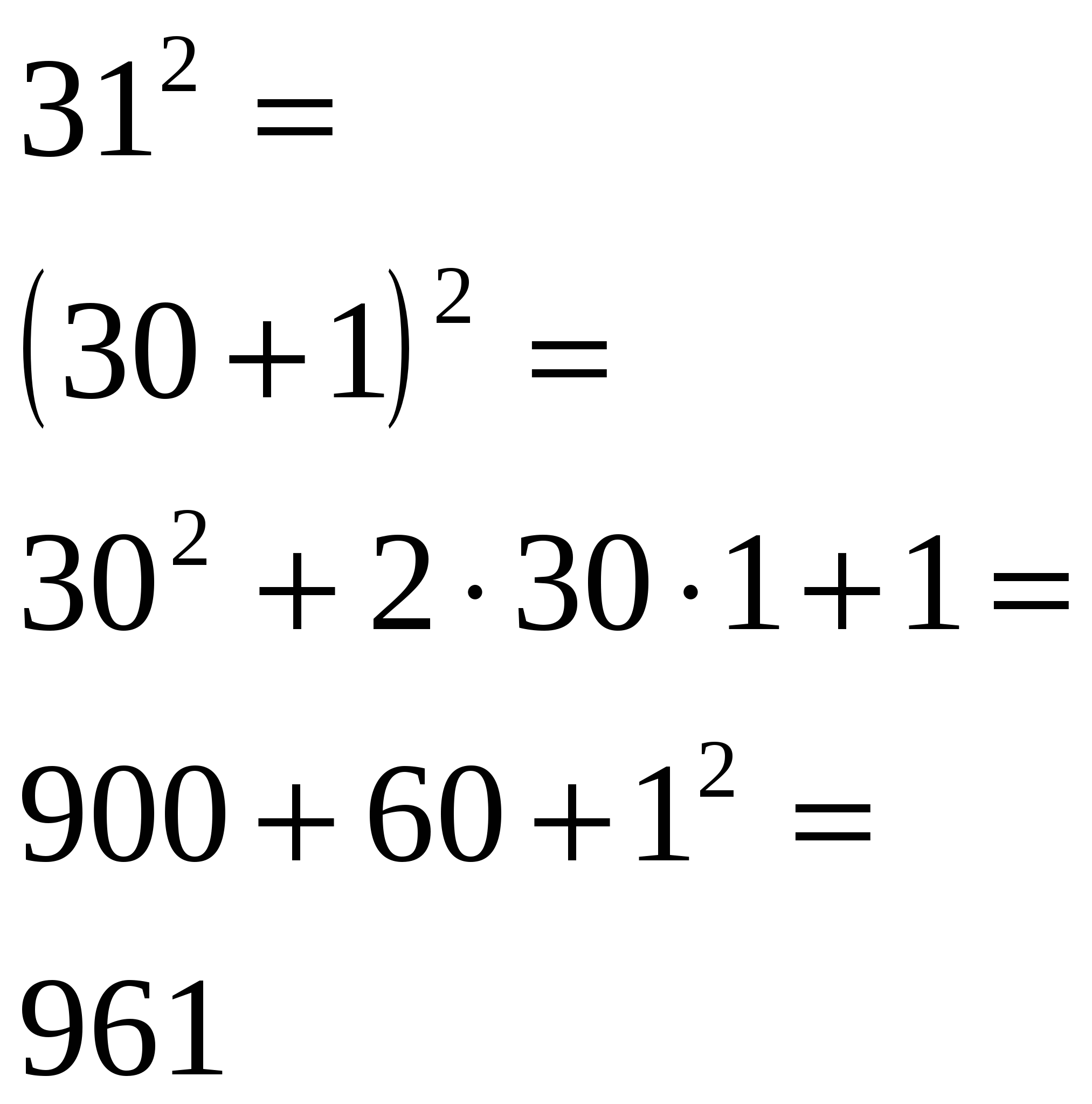
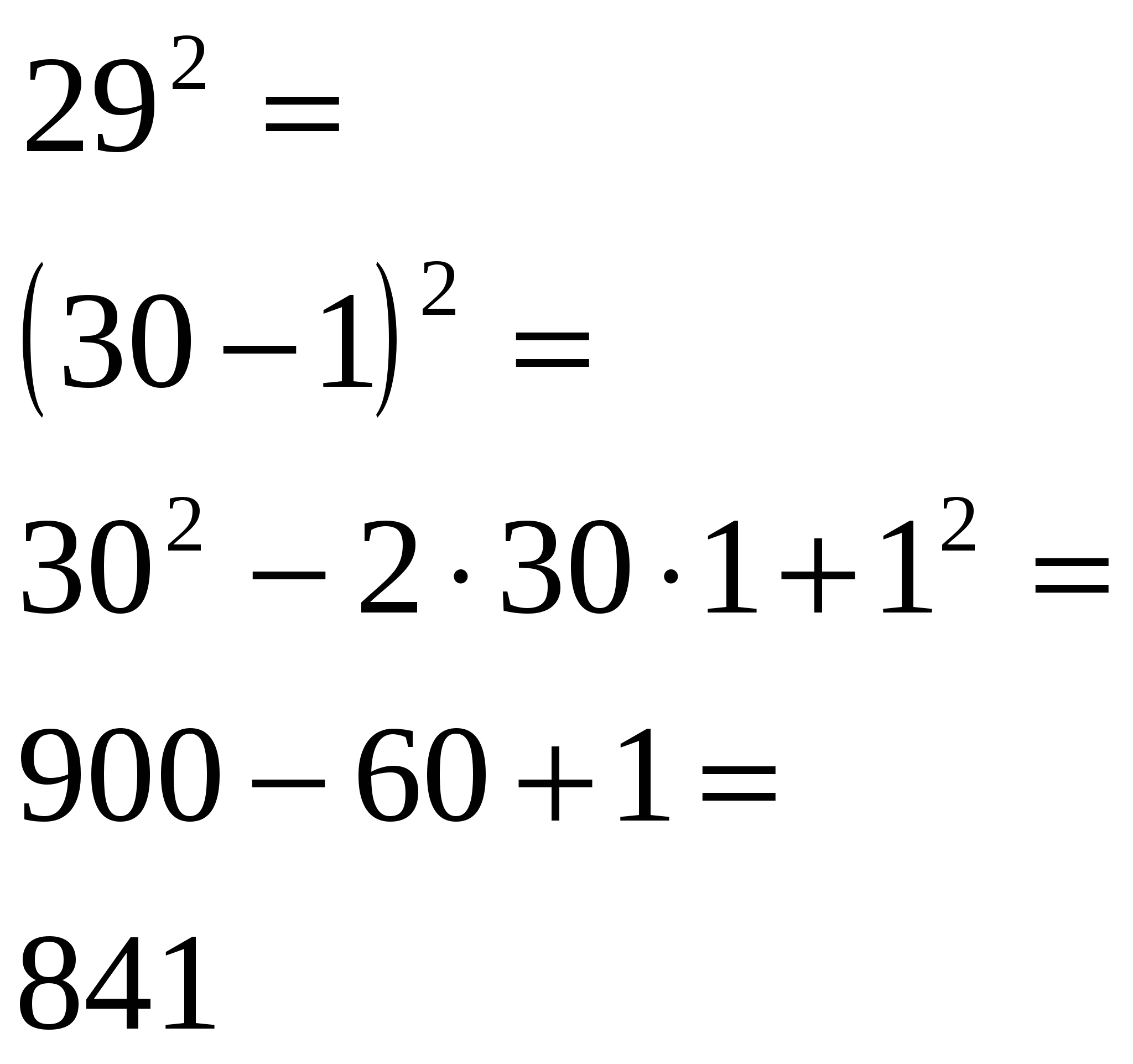
в ) г)
) г)
Ответы проверяются тут же на уроке. Если решение какого-либо примера не получилось у большинства учащихся, то его решение рассматривается на доске.
Самостоятельная работа (тетради взять на проверку).
Вариант 1:
1. Преобразуйте выражения:
а) (2x-5)2;
б) (3а + b2)2
2. Докажите, что (-а-b)2=(а+b)2
3. Дополните до квадрата суммы и квадрата разности:
а) а2+2аb+ ▭=(а+b)2
б) n2-4mn+ ▭=(▭-▭)2
в) 4а6- ▭+ b2=(▭-▭)2
Не выполняя вычислений, сравните значения выражений (28+72)2 и 282+722
Вычислите, используя формулы сокращенного умножения:
а) 422
б) 1412-2∙141∙41+412
Вариант 2:
1. Преобразуйте выражения:
а) (5x-2)2;
б) (4а + b2)2
2. Докажите, что (x-2)2=(2-x)2
3. Дополните до квадрата суммы и квадрата разности:
а) а2-2аb+ ▭=(а-b)2
б) m2+6mn+ ▭=(▭+▭)2
в) 9а8+▭+ b4=(▭+▭)2
Не выполняя вычислений, сравните значения выражений (35+65)2 и 352+652
Вычислите, используя формулы сокращенного умножения:
а) 312
б) 552+2∙55∙25+252
Итог урока.
Домашнее задание.
п.17 (геометрическое доказательство формул),
№ 474-477(г) (выполнить классификацию примеров по принципу + и -),
№ 457.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ