Тема: Квадратный трехчлен и его корни.

Тип урока: урок обобщения и систематизации знаний, умений, навыков по теме «Квадратный трехчлен».

Цели урока:

• Образовательные: повторить определение квадратного трехчлена, сколько корней может иметь квадратный трехчлен; обобщить и систематизировать знания квадратного трехчлена, разложения квадратного трехчлена на множители; формировать навыки самоконтроля

• Развивающие: развивать у учащихся память, внимание, логику, познавательный интерес к предмету.

• Воспитательные: воспитывать аккуратность, формировать ценностное отношение к математическим понятиям, воспитывать культуру умственного труда, способствовать развитию интереса к предмету, организованности, мировоззренческих понятий.

Формы организации познавательной деятельности: фронтальная работа, сочетающаяся с общеклассной; частично – поисковый метод; индивидуальная работа; самоконтроль, взаимоконтроль.

Структура урока.

1. Организация класса.

2. Актуализация знаний учащихся.

3. Итог урока.

Оборудование: учебник Ю. Н. Макарычев, рабочие тетради, карточки с заданиями самостоятельной работы, компьютер, мультимедиа проектор.

Ход урока.

1. Организация класса.

Сообщение темы, целей урока.

-Здравствуйте ребята. Сегодня на уроке мы с вами обобщим знания квадратного трехчлена, разложения квадратного трехчлена на множители, а также повторим умение решать квадратные уравнения с помощью формулы.

Сегодня у нас урок немного необычный, так как нас сегодня пригласили на конференцию, где нам будут представлены задания корреспондентов различных газет и журналов.

Условия: Отвечать на все вопросы

У каждого из вас на столе лежит Оценочный лист, в котором вы будете оценивать каждый вид работы на уроке.

2. Актуализация знаний учащихся.

1. Пригласительный билет.

Но вначале нам надо получить пригласительный билет. Для этого надо подписать фамилию и имя и заполнить пустые клеточки этого билета.

Пригласительный билет

Фамилия Имя:________________________________

Уравнение

a

b

c

b² - 4ac

x₁

x₂

х² - 7x + 12 = 0

1

-7

12

1

3

4

5х² - 7x - 6 = 0

5

-7

-6

169

-0,6

2

Теперь, получив билет, мы можем отвечать на вопросы корреспондентов.

Теперь оцените себя в Оценочном листе.

2. Вопрос №1.

Карточка № 1. Подпишите её.

Корреспондент журнала «Теорем парк»: предлагает

Заполнить пропуски в предложениях.

Теперь поменяйтесь карточками и проверьте, правильно ли записано у вашего соседа по парте. Теперь возьмите свои карточки обратно и оцените себя в Оценочном листе.

3. Вопрос № 2.

Устно: Корреспондент газеты «Из головы в голову»: предлагает

Решить устно уравнения: Ответы:

1) 2 х ² – 4х = 0 1) х₁ = 0, х₂ = 2

2) 6 х ² = 0 2) х = 0

3) х ² - 16 = 0 3) х₁ = -4, х₂ = 4

4) 3 x² + 1 = 0 4) Корней нет

Теперь оцените себя в Оценочном листе

Вот мы с вами устно выполнили задания этого корреспондента. А следующий корреспондент нам предлагает узнать первый вычислительный прибор…

4. Вопрос № 3.

Устно: Корреспондент журнала «Из истории ЭВМ »: предлагает

Вопрос: Назовите первый вычислительный прибор, который появился около 2500 лет назад и был широко распространён в Египте, Китае, Греции.

Ответ: Абак.

Историческая справка: Абак служил не столько для облегчения собственно вычислений, сколько для запоминания промежуточных результатов. Известны разновидности абака: собственно абак (греческий или египетский) в виде дощечки, на которой проводили линии или выдалбливали желобки, в которые колонками клали камешки; китайский суан-пан и японский соробан с шариками, нанизанными на прутики. Русский абак – счеты – появились приблизительно в 16 или 17 веке. Они использовали десятичную, а не пятеричную систему счисления, как остальные абаки. Основная заслуга изобретателей абака – создание позиционной системы представления чисел.

Теперь оцените себя в Оценочном листе

5. Вопрос № 4.

Корреспондент газеты «Дружите с множителями»: предлагает

Решить в тетрадях и на доске № 78 (а, б)

а) 2х² + 12х – 14 = 2 (х + 7)(х – 1)

2х² + 12х – 14 = 0

х² + 6х – 7 =0

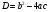
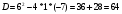
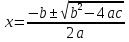
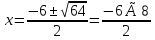
х₁ = -7, х₂ = 1

Ответ: 2х² + 12х – 14 = 2 (х + 7)(х – 1)

_{б) –m}² _{+5m –6 = -(m –2)(m - 3) = (2 – m)(m –3)}

_–m² _{+5m –6 =0}

_m² _{-5m +6 =0}

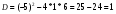
_{m1= 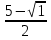=2, m2=}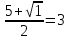

Ответ: _–m² _{+5m –6 = -(m –2)(m - 3) = (2 – m)(m –3)}

Теперь оцените себя в Оценочном листе

6. Вопрос № 5.

Устно: Корреспондент журнала «Мир чисел»: предлагает

Вопрос: Назовите числа, которые в древности назывались «фальшивыми» числами.

Ответ: Отрицательные числа.

Историческая справка: Понятие числа зародилось в глубокой древности. На протяжении веков это понятие подвергалось расширению и обобщению. Отрицательные числа долгое время считали «фальшивыми» и истолковывали как «долг», как недостачу. Правила действий над положительными и отрицательными числами длительное время рассматривались лишь для случаев сложения и вычитания. Например, индийские математики VII в. Так формулировали эти правила: «Сумма двух имуществ есть имущество, сумма двух долгов есть долг, сумма имущества и долга равна их разности». Лишь в XVII в. С использованием метода координат отрицательные числа были признаны в качестве равноправных с положительными.

Теперь оцените себя в Оценочном листе

7. Вопрос № 6.

Корреспондент газеты «Скоро экзамен»: предлагает

Выполнить задания теста.

Теперь проверим.

1. Г 1. Б

2. (х - 3)² + 2 2. (х - 3)² + 6

3. В 3. В

4. 4.

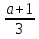
5. А 5. Б

Теперь оцените себя в Оценочном листе

8. Вопрос № 7.

Корреспондент газеты «Знаете ли вы…»: предлагает

Историческая справка: У Пифагора было много учеников, которых он обучал в течение 15 лет. Первые пять лет они должны были молчать: это приучало их к сосредоточенности. Вторые пять лет ученики могли только слушать речи учителя, но не видеть его: Пифагор говорил с ними ночью и из-за занавеси. И только последние пять лет ученики могли беседовать с учителем лицом к лицу.

Вопрос:

• Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы?

• Вот сколько, - ответил философ. – Половина изучает математику, четверть – музыку. Седьмая часть пребывает в молчании, и, кроме того, есть ещё три женщины.

• Сколько же учеников посещали школу Пифагора?

Ответ: Школу посещали 28 человек; из них математикой занимались 14, музыкой – 7, находились в молчании 4 человека и 3 женщины.

3. Итог урока.

На этом наша конференция подошла к концу. Надеемся, что сегодняшняя игра пробудила у вас интерес и к истории математики, и к математике, расширила ваш кругозор. И ещё хотелось бы, чтобы все участники и гости знали главное. Мир полон тайн и загадок. Но разгадать их могут только

пытливые и любознательные. Открытия ждут вас. Будьте настойчивы.

Вопрос № 7. Корреспондент газеты «Знаете ли вы…»:

Вопрос:

• Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы?

• Вот сколько, - ответил философ. – Половина изучает математику, четверть – музыку. Седьмая часть пребывает в молчании, и, кроме того, есть ещё три женщины.

• Сколько же учеников посещали школу Пифагора?

Вопрос № 7. Корреспондент газеты «Знаете ли вы…»:

Вопрос:

• Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы?

• Вот сколько, - ответил философ. – Половина изучает математику, четверть – музыку. Седьмая часть пребывает в молчании, и, кроме того, есть ещё три женщины.

• Сколько же учеников посещали школу Пифагора?

Вопрос № 7. Корреспондент газеты «Знаете ли вы…»:

Вопрос:

• Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы?

• Вот сколько, - ответил философ. – Половина изучает математику, четверть – музыку. Седьмая часть пребывает в молчании, и, кроме того, есть ещё три женщины.

• Сколько же учеников посещали школу Пифагора?

Вопрос № 7. Корреспондент газеты «Знаете ли вы…»:

Вопрос:

• Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы?

• Вот сколько, - ответил философ. – Половина изучает математику, четверть – музыку. Седьмая часть пребывает в молчании, и, кроме того, есть ещё три женщины.

• Сколько же учеников посещали школу Пифагора?